Kurs:Mathematik für Anwender (Osnabrück 2019-2020)/Teil II/Arbeitsblatt 37/kontrolle
- Übungsaufgaben
Beschreibe (ohne weitere Begründung) den Lauf des Sekundenzeigers einer Uhr als eine differenzierbare Kurve auf dem Einheitskreis (der Zeiger soll also im Zeitintervall eine Runde im Uhrzeigersinn drehen und zum Zeitpunkt „oben“ starten).
Zeige, dass der Grenzwert einer Funktion in einem Berührpunkt der Definitionsmenge im Falle der Existenz eindeutig bestimmt ist.
Es sei ein metrischer Raum, sei eine Teilmenge und sei ein Berührpunkt von . Es sei
eine Abbildung in einen euklidischen Vektorraum mit den Komponentenfunktionen
bezüglich einer Basis von . Zeige, dass der Limes
genau dann existiert, wenn sämtliche Limiten
existieren.
Es sei ein metrischer Raum und eine Teilmenge. Es sei
eine stetige Abbildung in einen weiteren metrischen Raum und sei ein Punkt, der ein Berührpunkt von ist. Zeige, dass der Grenzwert
existiert.
Es sei eine Teilmenge eines metrischen Raumes, ein Berührpunkt von ,
eine Abbildung in einen weiteren metrischen Raum und . Zeige, dass für den Limes
genau dann gilt, wenn
gilt.
Es seien metrische Räume und sei
eine stetige Abbildung. Es sei ein Berührpunkt von und
ein Berührpunkt von . Es sei
eine Abbildung und es sei vorausgesetzt, dass
existiert. Zeige, dass dann auch
existiert und mit übereinstimmt.
Es sei ein euklidischer Vektorraum und . Zeige, dass die Abbildung
differenzierbar ist mit der Ableitung .
Es sei ein reelles Intervall und ein euklidischer Vektorraum. Es seien
zwei in differenzierbare Kurven und es sei
eine in differenzierbare Funktion. Zeige, dass folgende Aussagen gelten.
- Die Summe
ist in differenzierbar mit
- Das Produkt
ist differenzierbar in mit
Insbesondere ist für auch differenzierbar in mit
- Wenn nullstellenfrei ist, so ist auch die Quotientenfunktion
in differenzierbar mit
Es seien
differenzierbare Kurven. Berechne die Ableitung der Funktion
Formuliere das Ergebnis mit dem Skalarprodukt.
Wir betrachten die Funktionen
Es seien drei Vektoren. Wir definieren die Kurve
a) Berechne und .
b) Berechne .
c) Zeige, dass ein Vielfaches von und ein Vielfaches von ist.
d) Skizziere für , und das Bild der Kurve für .
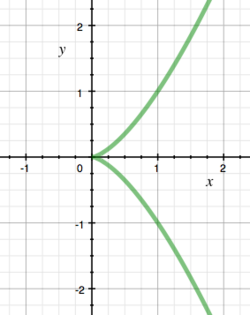
Das Bild der durch
definierten Kurve heißt Neilsche Parabel. Zeige, dass ein Punkt genau dann zu diesem Bild gehört, wenn er die Gleichung erfüllt.
Wir können durch Einsetzen direkt nachrechnen, dass die Bildpunkte der Kurve die beschreibende Gleichung erfüllen, denn es gilt . Das bedeutet, dass jeder Bildpunkt in der Menge derjenigen Punkte enthalten ist, für die gilt.
Umgekehrt können wir sehen, dass auch jeder Punkt, für den gilt, auch ein Bildpunkt der Kurve ist. Dazu müssen wir zu vorgegebenem ein finden, sodass und gilt. Es bietet sich hier an, zu definieren, weil das Ziehen der dritten Wurzel eine Bijektion auf ganz ist. Nach Wahl von gilt also und wir können nachrechnen, dass auch gilt, wobei wir ausnutzen, dass auf der Kurve liegt.
Wir haben nun also gezeigt, das zwei zueinander äuqivalente Beschreibungen vorliegen: im ersten Fall als Bild einer parametrischen Darstellung (die vom Parameter abhängt), im zweiten als implizite Beschreibung (als die impliziten Lösungen einer Gleichung). In diesem Fall besteht die implizite Beschreibung sogar nur aus Polynomen, sodass die Kurve auch als algebraische Kurve bezeichnet wird. Dazu gibt es eine umfangreiche Theorie, die wir hier jedoch nicht im Detail behandeln.
Es sei
Bestimme die Punkte , für die der Abstand der zugehörigen Kurvenpunkte zum Punkt minimal wird.
Wir betrachten die Kurve
a) Zeige, dass die Bildpunkte der Kurve die Gleichung
erfüllen.
b) Zeige, dass jeder Punkt
mit
zum Bild der Kurve gehört.
c) Zeige, dass es genau zwei Punkte
und
mit identischem Bildpunkt gibt, und dass ansonsten die Abbildung injektiv ist.
Es sei
eine differenzierbare Kurve und ein Punkt. Es sei derart, dass der Abstand (zwischen und einem Kurvenpunkt) in minimal werde. Zeige, dass senkrecht zu ist.
Die zu zeigende Aussage besagt, dass der Richtungsvektor der Kurve in Punkt orthogonal steht zur Richtung, die von zum Punkt zeigt, falls in der Abstand zu minimiert wird. Anschaulich ist dies naheliegend, weil andernfalls durch kleine Störung an ein Punkt auf der Kurve erreicht wird, der noch näher an liegt: Zum Beispiel sollte dies für oder der Fall sein, wenn eine sehr kleine positive Zahl ist.
Um nun die Aussage zu zeigen, können wir uns von zwei Seiten nähern. Wir betrachten zunächst die Schlussfolgerung. Die Aussage, dass die beiden Vektoren senkrecht zueinander stehen, lässt sich formulieren als
da wir mit einem euklidischen Skalarprodukt arbeiten. Hierbei sollen die Komponenten von bzw. bezüglich einer Orthogonalbasis, zum Beispiel der Standardbasis, bezeichnen.
Andererseits ist die Zuordnung eine differenzierbare Funktion. Nach Satz 15.3 wissen wir, dass die Ableitung einer solchen Funktion in einem Minimum verschwindet. Es bleibt also die Ableitung von
im Punkt zu bestimmen. Dies ist eine gute Übung, um die Ableitungsregeln, insbesondere die Kettenregel, zu wiederholen. Dabei muss man das Summenzeichen wegen der Additionsregel nicht auflösen. Wie schließt man nun aus dem ermittelten Wert der Ableitung darauf, dass das zuvor berechnete Skalarprodukt Null wird? Dabei sollte man auch den Fall beachten, dass eventuell auf der Kurve liegt und somit ist.
Es sei der Graph der reellen Betragsfunktion. Man gebe eine differenzierbare Kurve
an, deren Bild genau ist.
Die Betragsfunktion selbst ist nicht differenzierbar, sondern hat einen Knick, sodass die Existenz einer differenzierbaren Kurve, deren Bild ist, auf den ersten Blick unintuitiv erscheinen mag. Die naheliegende Parametrisierung
ist offenbar nicht differenzierbar, weil die zweite Koordinatenfunktion keine differenzierbare Funktion ist.
Anschaulich lässt sich diese Aufgabe als die Beobachtung interpretieren, dass man mit einem Fahrzeug bei hoher Geschwindigkeit nicht durch eine sehr scharfe Kurve fahren kann. Bei niedriger Geschwindigkeit ist das aber kein Problem. Je langsamer man fährt, desto schärfer kann man abbiegen. In unserem Fall haben wir es mit einem rechtwinkligen Knick zu tun, was sich als Grenzfall auffassen lässt, bei dem wir die Geschwindigkeit im Knickpunkt auf Null reduzieren. Außerhalb des Knickpunkts muss die Geschwindigkeit aber größer als Null sein, damit wir uns überhaupt bewegen.
Eine geeignete Parametrisierung der Kurve ist . Das Bild dieser Kurve ist genau , weil eine Bijektion auf ist. Die Differenzierbarkeit kann koordinatenweise gezeigt werden, zum Beispiel mit Hilfe von Aufgabe 15.1. Wie folgt das genau und was ist die Ableitung der Kurve? Ist sie tatsächlich Null für ?
Die folgende Aufgabe setzt das Konzept Äquivalenzrelation voraus.
Es sei ein Punkt und sei . Wir betrachten die Menge
Wir nennen zwei Kurven tangential äquivalent, wenn
ist.
a) Zeige, dass dies eine Äquivalenzrelation ist.
b) Finde den einfachsten Vertreter für die Äquivalenzklassen.
c) Man gebe für jede Klasse einen weiteren Vertreter an.
d) Beschreibe die Menge der Äquivalenzklassen (also die Quotientenmenge).
Es sei ein euklidischer Vektorraum der Dimension und Punkte mit
Zeige, dass es eine stetig differenzierbare Kurve
mit , und für alle gibt.
Es seien endlich viele Punkte und sei . Zeige, dass es zu je zwei Punkten eine differenzierbare Kurve
mit und gibt.
- Aufgaben zum Abgeben
Aufgabe (5 (1+2+2) Punkte)Referenznummer erstellen
Betrachte die Kurve
a) Bestimme die Ableitung von in jedem Punkt .
b) Bestimme die Komponentenfunktionen von bezüglich der neuen Basis
von .
c) Berechne die Ableitung in der neuen Basis direkt und mit Hilfe von Lemma 37.10.
Aufgabe (3 Punkte)Referenznummer erstellen
Für welche Punkte ist der Abstand der Bildpunkte der Kurve
Aufgabe (4 Punkte)Referenznummer erstellen
Wir betrachten die Abbildung
die einem Punkt den eindeutigen Schnittpunkt der durch die beiden Punkte und gegebenen Geraden mit dem Einheitskreis
zuordnet. Zeige, dass diese Abbildung wohldefiniert ist und bestimme die funktionalen Ausdrücke, die diese Abbildung beschreiben. Zeige, dass differenzierbar ist. Ist injektiv, ist surjektiv?
Auf einem Jahrmarkt befindet sich ein „Doppel-Karussell“, bei dem sich ein Sitz alle Sekunden um einen kleinen Kreis mit Radius Meter dreht, wobei sich der Mittelpunkt dieses Kreises seinerseits alle Sekunden um einen großen Kreis mit Radius Meter dreht. Beide Drehungen sind im Uhrzeigersinn. Zum Zeitpunkt besitzt der Sitz zum Mittelpunkt den Abstand Meter.
a) Beschreibe diesen Bewegungsvorgang (in einem geeigneten Koordinatensystem) als eine differenzierbare Kurve.[1]
b) Berechne den Geschwindigkeitsvektor dieser Bewegung zu jedem Zeitpunkt.
c) Berechne die Geschwindigkeit (den Betrag des Geschwindigkeitsvektors) dieser Bewegung zu jedem Zeitpunkt.
Aufgabe (6 Punkte)Referenznummer erstellen
Bestimme in der Situation von Aufgabe 37.24 die Zeitpunkte, an denen die Geschwindigkeit maximal oder minimal wird.
Aufgabe (5 Punkte)Referenznummer erstellen
- Fußnoten
- ↑ Gefragt ist hier nach der mathematischen Überlagerung der beiden Bewegungen, d.h. die große Bewegung verdreht nicht das Koordinatensystem der kleinen Bewegung. Eine volle Umdrehung des kleinen Kreises liegt vor, wenn der Verbindungspfeil aus dem äußeren Drehmittelpunkt und dem Sitz wieder in die gleiche Himmelsrichtung zeigt. Bei der mechanischen Überlagerung, die vorliegt, wenn die Umdrehungsgeschwindigkeit des äußeren montierten Motors feststeht, sieht dies anders aus.








![{\displaystyle {}[0,60]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43c27b825bed7a1e27fc4d0bb9b7c104fdebbcd0)

















































































































![{\displaystyle {}I={]{-1},1[}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3749617d69bf24a7c27c0e843088c78839cd93ea)





![{\displaystyle \gamma \colon [0,1]\longrightarrow V,\,t\longmapsto \gamma (t),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2d32baca51a0f6a0e599638517ee8e4e9752cc8)



![{\displaystyle {}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b82d90b07769530e83a657ede98f1649efa31f)



![{\displaystyle \varphi \colon [0,1]\longrightarrow M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/690275286b6772e6531021063cf77d3547f3d36a)



















