Modellierungsthema

Wir wollen herausfinden, in welchem Jahr die Malediven überschwemmt sind. Grund dieses Phänomens ist der jährliche Anstieg des Meeresspiegels.

Ziele

Darstellung einer spezifischen Insel der Malediven
Darstellen einer Funktion, die den Meeresspielanstieg verdeutlicht
Meeresspiegelanstieg und Fläche der Malediven in Zusammenhang bringen

Technische Werkzeuge:

Im OLAT befindet ist im Materialordner nun eine csv Datei der geographischen Daten, die in Octave eingelesen werden können, siehe die Skript 'Malediven'. Allerdings sieht die Insel anders aus, wieso?

Mathematische Werkzeuge für das Modell

Sekundarstufe I

Datenrecherche des Insel, bzgl. Höhe und Größe
Datenrecherche der Höhe des Meeresspiegels
Datenrecherche und in Tabellenform bringen
Diagramme erstellen, z.B. ein Säulendiagramm
Summe berechnen mithilfe der Tabellenkalkulation
Mittelwert berechnen der Jahre und des Anstiegs
Programme: Tabellenkalkulation

Sekundarstufe II

Trendlinie erstellen
Regressionsgerade berechnen
Arbeiten mit der Regressionsgerade
Satellitenbilder Auswertung
Programme: Tabellenkalkulation, GeoGebra

Uni

Lineare Regression berechnen
Matrixdarstellung in Octave
Matrizen zusammenfügen (Wasser-und Inselmatrix)

Modellierungszyklen

Zyklus 1: Insel in Matrix überführen

Villingili, auch Wilingili genannt, ist die Insel, die wir darstellen. Sie gehört zum Addu-Atoll (Seenu). Dort befindet sich die höchste Erhebung der Malediven mit zwei Metern über dem Meeresspiegel. Dies ist der Grund, weshalb wir uns für diese Insel entschieden haben.

Mit Hilfe einer Satellitenaufnahme, die zeigt, welcher Teil der Insel bei welcher Erhöhung untergeht, haben wir eine 20x28 Matrix erstellt:

A=

   0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    5    6    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    9    7    6    6    7    6  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    9    9    9    9    7  5
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    9    7    7    7  5
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    0   13    9    9    9  6
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    9    9    9    9  3
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    9    9    9    7  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    9    9    9    3  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    7    7    4    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    5    3    3    0    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    6    3    0    0    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    0    5    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    3    2    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    0    3    0    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    0    0    0    2    0    0    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    0    2    4    0    0    0    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    1    2    0    0    0    0    0    0    0    0  0
   0    0    0    0    0    0    0    0    0    3    3    0    0    0    0    0    0    0    0  0
   0    0    0    0    0    0    0    0    3    1    1    0    0    0    0    0    0    0    0  0
   0    0    0    0    0    0    0    5    2    0    0    0    0    0    0    0    0    0    0  0
   1    0    0    0    0    0    3    4    0    0    0    0    0    0    0    0    0    0    0  0
   0    0    0    1    0    0    3    0    0    0    0    0    0    0    0    0    0    0    0  0
   0    0    1    2    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0  0
   0    1    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0  0
   0    0    0    1    0    0    0    0    0    0    0    0    0    0    0    0    0    0    0  0

Verbesserung des Zyklus 1: Insel in Matrix überführen

Um eine genauere Annäherung der Insel zu erhalten wurden die Quadrate, mit deren Hilfe die vorherige Matrix erstellt wurde, verkleinert. Diese wurden mit Hilfe des Programmes GeoGebra eingeteilt. Dabei wurde jedes größere Quadrat in weitere kleinere geteilt. Die vorherige Einteilung der Quadrate lieferte jeweils einen Flächeninhalt von 1ha. Durch die Verkleinerung dieser, blieb ein Flächeninhalt pro Quadrat von 0,25ha übrig.

Da hier das Problem auftauchte, dass ein eingeteiltes Quadrat beispielsweise zur Hälfte aus Wasser und zur Hälfte aus Insel bestand, wurde auch hier mit Hilfe von GeoGebra eine Gewichtung durchgeführt. Um eine möglichst realitätsnahe Abbildung der Insel zu erhalten, wurde jeweils an den Randpunkten der Insel bestimmt zu welchem Prozentanteil Land, beziehungsweise Wasser vorhanden war. Diese Daten wurden in einem Tabellenkalkulationsprogramm (Excel) eingegeben um eine erste Ansicht der Matrix, die die Insel repräsentiert zu erhalten. Im unteren Bild ist die Matrix in der Excel-Datei abgebildet.

Zyklus 2: Matrix Darstellung in Octave

Um genauere Werte zu bekommen, haben wir die Matrix in Octave interpoliert. Interpolation bezeichnet dabei eine Klasse von Problemen und verfahren, um zu gegebenen diskreten Daten eine stetige Funktion zu finden, die diese Daten abbildet. Man sagt die Funktion interpoliert die Daten.

In Octave haben wir jedoch die kubische-Spline Interpolation verwendet, da diese die Daten Stückweise mit einem Polynom dritten Grades approximiert. In der Mathematik ist die bikubische Interpolation eine Erweiterung der kubischen zum Interpolieren von Datenpunkten auf einem zweidimensionalen regulären Gitter . Die interpolierte Oberfläche ist glatter als die entsprechenden Oberflächen, die durch bilineare Interpolation oder Interpolation zum nächsten Nachbarn entsteht. Für eine Anwendung der bikubischen Splint-Interpolation, müssen die zu interpolierenden Punkte $z_{ij}$ in einem rechteckigen Gitter angeordnet sein. Jede zwischen vier Punkten aufgespannte Fläche $A_{ij}$ wird durch ein zweidimensionales Polynom von 16 Koeffizienten charakterisiert:

z:=A_{ij}(x,y)=\sum _{k=0}^{3}\sum _{l=0}^{3}a_{k,l}^{ij}\cdot x^{k}\cdot y^{l}={\begin{matrix}a_{0,0}^{ij}&+&a_{1,0}^{ij}\cdot x&+&a_{2,0}^{ij}\cdot x^{2}&+&a_{3,0}^{ij}\cdot x^{3}&+\\a_{0,1}^{ij}\cdot y&+&a_{1,1}^{ij}\cdot x\cdot y&+&a_{2,1}^{ij}\cdot x^{2}\cdot y&+&a_{3,1}^{ij}\cdot x^{3}\cdot y&+\\a_{0,2}^{ij}\cdot y^{2}&+&a_{1,2}^{ij}\cdot x\cdot y^{2}&+&a_{2,2}^{ij}\cdot x^{2}\cdot y^{2}&+&a_{3,2}^{ij}\cdot x^{3}\cdot y^{2}&+\\a_{0,3}^{ij}\cdot y^{3}&+&a_{1,3}^{ij}\cdot x\cdot y^{3}&+&a_{2,3}^{ij}\cdot x^{2}\cdot y^{3}&+&a_{3,3}^{ij}\cdot x^{3}\cdot y^{3}&~\end{matrix}}

Für eine zweidimensionale Darstellung müssen die Koeffizienten so gewählt werden, dass die aus allen Flächen zusammengesetzte Funktion $S(x,y):\mathbb {R} ^{2}\rightarrow \mathbb {R}$ zweimal stetig in x- und y-Richtung differenzierbar ist. Das heißt, neben S selbst sind die folgenden Ableitungen stetig auf ganz : $\mathbb {R} ^{2}$

{\begin{matrix}{\frac {\partial S(x,y)}{\partial x}},&{\frac {\partial S(x,y)}{\partial y}},&{\frac {\partial ^{2}S(x,y)}{\partial x^{2}}},&{\frac {\partial ^{2}S(x,y)}{\partial y^{2}}},&{\frac {\partial ^{2}S(x,y)}{\partial x\partial y}},&{\frac {\partial ^{3}S(x,y)}{\partial x^{2}\partial y}},&{\frac {\partial ^{3}S(x,y)}{\partial x\partial y^{2}}},&{\frac {\partial ^{4}S(x,y)}{\partial x^{2}\partial y^{2}}}\end{matrix}}

Jede Teilfäche $A_{i,j}$ , die durch 4 Punkte aufgespannt wird, kann durch ein kubisches Polynom mit vier Koeffizienten, welches parallel zur x-Achse oder y-Achse läuft, beschrieben werden. Zu jeder Fläche $A_{i,j}$ , welche das zweidimensionale Polynom beschreibt, stehen vier eindimensionale Randpolynome mit 16 Koeffizienten: $s_{x~i,j},s_{x~i,j+1},s_{y~i,j},s_{y~i+1,j}$ . Um diese Randpolynome von den Teilflächen $A_{i,j}$ "zusammenzurechnen" ist es erforderlich, ein System von 16 linearen Gleichungen aufzustellen. Die Matrix A1 wurde nun in Octave eingegeben und mit dem Befehl der kubischen-Interpolation dargestellt. (Bilder siehe unten)

Die erweiterte und verbesserte Matrix A1:

$A1={\begin{matrix}[00000000000000000000000000000000000000000\\00000000000000000000000000000000000000000\\00000000000000000000000000000000000000000\\00000000000000000000000000000000000000000\\00000000000000000000000000000000000000000\\00000000000000000000000560000000000000000\\00000000000000000000000976676000000000000\\00000000000000000000000099997500000000000\\00000000000000000000000009777500000000000\\000000000000000000000000013999600000000000\\00000000000000000000000009999300000000000\\000000000000000000000000099137000000000000\\00000000000000000000000009993000000000000\\00000000000000000000000007740000000000000\\00000000000000000000000053300000000000000\\00000000000000000000000063000000000000000\\00000000000000000000000050000000000000000\\00000000000000000000000320000000000000000\\00000000000000000000000300000000000000000\\00000000000000000000002000000000000000000\\00000000000000000000240000000000000000000\\00000000000000000001200000000000000000000\\00000000000000000003300000000000000000000\\00000000000000000031100000000000000000000\\00000000000000000520000000000000000000000\\00000000001000003400000000000000000000000\\00000000000001003000000000000000000000000\\00000000000012000000000000000000000000000\\00000000000100000000000000000000000000000\\00000000000001000000000000000000000000000\\00000000000000000000000000000000000000000\\00000000000000000000000000000000000000000\\00000000000000000000000000000000000000000\\00000000000000000000000000000000000000000\\00000000000000000000000000000000000000000]\end{matrix}}$

Die 3D-Darstellungen der A1 Matrix und der interpolierten Matrix:

Verbesserung des Zyklus 2: Matrix Darstellung in Octave

Die gewonnen Daten aus den Satelliten aufnahmen, bezüglich der Höhe, entsprechen hier nicht der Realität. Diese liefern, wie in der Abbildung zu sehen eine maximale Höhe der Insel von 13m. Zu beachten ist hier, dass die gewonnenen Satellitenbilder nicht berücksichtigen ob der Boden der Insel dieser Höhe entspricht. Hier wurden vermutlichen die auf der Insel befindlichen Palmen mit berücksichtigt, sowie eventuell erbaute Gebäude. Die Insel hat nach Recherchen eine reale Höhe von 2,4m. Um also eine reale Abbildung der Insel in Octave zu erhalten, wurde die Insel mit dem Faktor $a$ :

a=2,4/13

a=0,1846

multipliziert. Das liefert eine geänderte Matrix, deren Höhe der Realität entspricht. Zu sehen ist hier der Plot der gewichteten Matrix. Diese wurde ebenfalls in Octave Interpoliert und dargestellt. Dabei erkennt man hier einen besseren Übergang zwischen Meer und Insel.

Zyklus 3: Meeresspiegelanstieg im Laufe der Zeit (Jahren)

Wir haben die Daten des Meeresspiegelanstiegs gesammelt und in einer Exceltabelle zusammengetragen. Die Daten beginnen im Jahr 1961 und reichen bis ins Jahr 2008, wobei der Meeresspiegel bis 1992 jährlich um 1,8mm und ab 1993 um 3,1mm gestiegen ist. Ab dem Jahr 2004 steigt er nur noch jährlich um 2,5mm.

Säulendiagramm des Meeresspiegelanstiegs von 1961-2008

Jahr	Meeresspiegel in mm
1900	0
1961	1,8
1962	3,6
1963	5,4
1964	7,2
1965	9
1966	10,8
1967	12,6
1968	14,4
1969	16,2
1970	18
1971	19,8
1972	21,6
1973	23,4
1974	25,3
1975	27
1976	28,8
1977	30,6
1978	32,4
1979	34,2
1980	36
1981	37,8
1982	39,6
1983	41,4
1984	43,2
1985	45
1986	46,8
1987	48,6
1988	50,4
1989	52,2
1990	54
1991	55,8
1992	57,6
1993	60,7
1994	63,8
1995	66,9
1996	70
1997	73,1
1998	76,2
1999	79,3
2000	82,4
2001	85,5
2002	88,6
2003	91,7
2004	94,2
2005	96,7
2006	99,2
2007	101,7
2008	104,2

Für die Jahre ab 2008 haben wir mithilfe von Excel den Meeresspiegel für die kommenden Jahrhunderte prognostiziert.

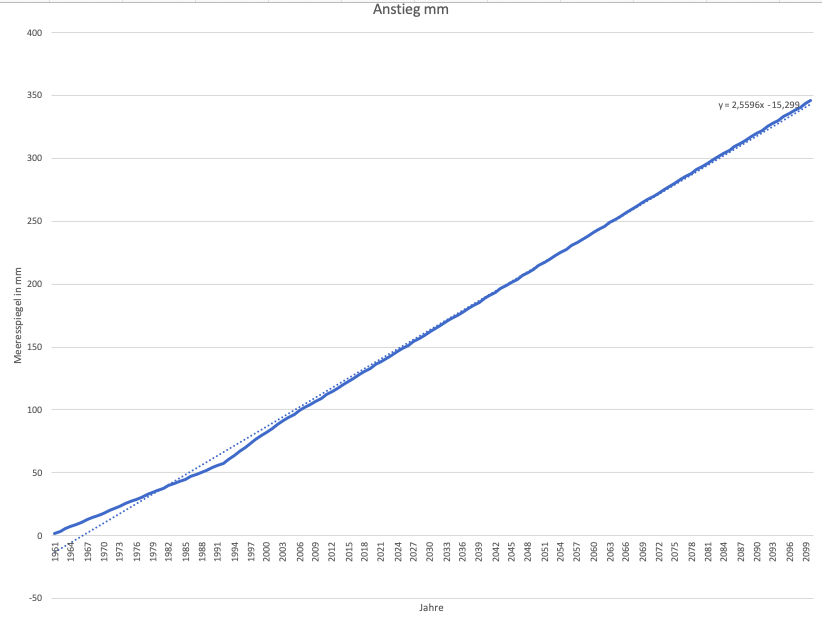
Jahr	Meeresspiegel in mm
2009	106,83004
2010	109,459734
2011	112,08942
2012	114,71922
2013	117,348815
2014	119,978509
2015	122,608203
2016	125,237897
2017	127,86759
2018	130,497284
2019	133,126978
2020	135,756672
2021	138,386365
2022	141,016059
2023	143,645753
2024	146,275447
2025	148,90514
2026	151,534834
2027	154,164528
2028	156,79422
2029	159,423915
2030	162,053609
2031	164,683303
2032	167,312997
2033	169,94269
2034	172,572384
2035	175,202078
2036	177,831772
2037	180,461465
2038	183,091159
2039	185,720853
2040	188,350547
2041	190,98024
2042	193,609934
2043	196,239628
2044	198,869322
2045	201,499015
2046	204,128709
2047	206,758403
2048	209,388097
2049	212,01779
2050	214,647484
2051	217,277178
2052	219,906872
2053	222,536565
2054	225,166259
2055	227,795953
2056	230,425647
2057	233,05334
2058	235,685034
2059	238,314729
2060	240,944424
2061	243,574119
2062	246,203814
2063	248,833509
2064	251,463203
2065	254,092898
2066	256,722593
2067	259,352288
2068	261,981983
2069	264,611678
2070	267,241373
2071	269,871067
2072	272,500762
2073	275,130457
2074	277,760152
2075	280,389847
2076	283,019542
2077	285,649237
2078	288,278931
2079	290,908626
2080	293,538321
2081	296,168016
2082	298,797711
2083	301,427406
2084	304,057101
2085	306,686795
2086	309,31649
2087	311,946185
2088	314,57588
2089	317,205575
2090	319,83527
2091	322,464965
2092	325,09466
2093	327,724354
2094	330,354049
2095	332,983744
2096	335,613439
2097	338,243134
2098	340,872829
2099	343,502524
2100	346,132218

Zyklus 4: Zusammenfügung der Wasser- und Inselmatrix

In diesem Zyklus fügen wir zu der interpolierten Inselmatrix eine Wassermatrix mit verschiedenen Wasserhöhen hinzu.

Dabei lässt sich erkennen, dass keine Insel mehr vorhanden sein wird, wenn der Meeresspiegel eine Höhe von 13m erreicht hat.

Verbesserung des Zyklus 4

Um besser darzustellen ab wann kein Leben mehr auf der Insel möglich ist, wurde die Gesamtfläche der Insel betrachtet. Diese wurde mit Hilfe der Matrix und den Satellitenaufnahmen erstellt. Zunächst haben wir die Länge eines Quadrates bestimmt, welche über das Bild der Insel gelegt wurde. Eine Länge entspricht dabei $0,5cm$ . Der Maßstab dieses Bildes war dabei $500m:5cm$ .

Füge hier noch Bilder der skalierten und gewichteten matrix ein

Sek. II Niveau

Auf dem Sek. II Niveau, kann man nun, wie wir es im Vorfeld getan haben, eine Fläche approximieren, indem man die Insel mit einer geometrischen Figur beschreibt. Weiter kann man die Insel mit Qudraten auslegen, deren Größe man schon kennt, um die Gesamtfläche zu bestimmen. Da wir im Vorfeld die Insel in Quadrate eingeteilt haben, nutzen wir diese Möglichkeit. Schaut man sich die Insel an, dann gibt es bei einem Meeresspiegel anstieg von $1m$ , noch $139,3$ Qudrate mit einem Flächeninhalt von $2500m^{2}$ . Dies liefert also die folgende Rechnung:

$2500m^{2}*139,3=348250m^{2}$

Es existieren also bei einem Meeresspiegel anstieg von $1m$ noch $348250m^{2}$ der Fläche der Insel.

Dies kann man für verschiedene Anstiege des Meeresspiegels berechnen.

Allgemein kann man also die Fläche berechnen als:

$2500m^{2}$ * der vorhanden Quadrate = die restliche Fläche der Insel

Meeresspiegel bei 2m:

$2500m^{2}*134,3=335750m^{2}$

Meeresspiegel bei 3m

$2500m^{2}*120,267=335750m^{2}$

Meeresspiegel bei 4m:

$2500m^{2}*98,184=245460m^{2}$

Meeresspiegel bei 5m:

$2500m^{2}*86,724=216810m^{2}$

Meeresspiegel bei 6m:

$2500m^{2}*75,724=189310m^{2}$

Meeresspiegel bei 7m:

$2500m^{2}*56,894=142235m^{2}$

Meeresspiegel bei 8m:

$2500m^{2}*36,594=91485m^{2}$

Meeresspiegel bei 9m:

$2500m^{2}*29,29=73225m^{2}$

Meeresspiegel bei 13m:

$2500m^{2}*8=2000m^{2}$

Laut dem Experiment „Weltacker", benötigt ein Mensch zum überleben eine Ackerfläche, von durchschnittlich $2000m^{2}$ , um alle lebenswichtigen Nahrungsmittel, sowie Energiepflanzen anzubauen. Diese Überlegung führt dazu, dass bei einem Meeresspiegel von $9m$ noch durchschnittlich 36 Personen auf der Insel leben können. Bei $13m$ kann nach diesem Projekt jedoch nur noch ein Mensch auf der Insel überleben. Zu beachten ist, dass man hierbei davon ausgeht, das kein Import stattfindet, sondern die Insel sich selbst versorgt.

Zyklus 5: Erstellung der Regressionsgerade und Prognose

Um die Jahreszahl bestimmen zu können, berechnen wir mit unseren gegebenen Werten eine Regressionsgerade. Dabei nutzen wir den Mittelwert der Daten (hier beschriftet als Mitt X)

Um den Anstieg des Meeresspiegels ablesen zu können, ermitteln wir mithilfe der Regressionsanalyse eine (lineare) Regressionsgerade des Anstiegs in Abhängigkeit der Jahreszahlen. Wie in Zyklus 3 sind dabei die Jahreszahlen auf der X-Achse zu finden und die Meeresspiegelhöhe auf der Y-Achse. Die Werte für die Berechnung entnehmen wir aus Tabelle 2. Wir besitzen also das Zahlenpaar $(xj,yj)$ .Dabei ist $xj$ die Jahreszahl und $yj$ die Höhe des Meeresspiegels. Die gesammelten Daten liegen annähernd auf einer Funktion, die mit : $f(x)=a+bx$ beschrieben werden kann. Die Abweichung der Daten zu der Gerade bezeichnen wir mit Residuen, diese sollen dabei möglichst klein gehalten werden. Wir suchen nun eine lineare Funktion, für die : $\sum (f(xj)-yj)^{2}$ minimal wird. Wir suchen also reelle Zahlen a und b, so dass

\sum (a+bxj-yj)^{2}

minimal ist. Dabei nutzen wir die Formeln für

b={\frac {\sum (xj-{\bar {x}})*(yj-{\bar {y}})}{\sum (xj-{\bar {x}})^{2}}}

a={\bar {y}}-b*{\bar {x}}

Dabei erhalten wir für

b=2,12

a=-4163,34

Die Regressionsgerade lautet nun:

f(x)=2,12xj-4163,34

Aus Octave erhalten wir die Angabe, dass die Insel bei ca. 13m völlig überflutet ist. Um nun die Jahreszahl zu ermitteln, wann dies der Fall sein wird, setzen wir die 13m in die Regressionsgerade ein. Dabei ist zu beachten, dass man nicht mit 13m rechnet, sondern mit 13000mm.

13000=2,12xj-4163,34

xj=8095

Im Jahre 8095 hat der Meeresspiegel eine Höhe von 13m,wenn der Meeresspiegel weiterhin so ansteigt. Im Jahre 8095 werden keine Malediven mehr sichtbar sein.

Um herauszufinden, wie stark der Zusammenhang zwischen x und y ist, berechnen wir den Korrelationskoeffizient $r$ . Dabei gilt:

Ist

r=1

so lässt sich der Wert von y gut mit dem Wert von x darstellen

Ist

r=0

so kann man kaum etwas über den Zusammenhang der Werte sagen

Ist

r>0

so sind die Werte positiv korreliert

Ist

r<0

so sind die Werte negativ korreliert

r={\frac {Sxy}{{\sqrt {(}}Sxx*Syy)}}

r=0,9913

Also lässt sich ein Zusammenhang der Variablen feststellen, dies beweist keine Kausalität!

Modellierungsalternativen

Zu beachten ist, dass wir in unserem Modell nicht berücksichtigt haben, dass sich die Ozeane jährlich erwärmen, sich das Wasser ausdehnt und der Meeresspiegel dabei schneller steigen könnte. Ebenso haben wir die geographische Beschaffenheit um die Insel nicht betrachtet, den z.B auch das Korallenriff hält das Wasser zurück und kann so den Anstieg verlangsamen. Umweltkatastrophen, die für einen Anstieg sorgen können, haben wir nicht in Betracht gezogen. Diese Faktoren könnte man in einem erweiterten Modell miteinbeziehen, um genauere Werte des Untergangs zu bekommen.

Fazit

Die Insel Villingili (Addu-Atoll) wird im Jahr 8093 untergehen. Diese Jahreszahl ist ziemlich hoch und kommt so zustande, dass wir durch die Auswertung der Satellitenbilder eine Höhe der Insel von 13m angenommen haben. In der Literatur jedoch ist für die höchste Erhebung der Wert 5,1m zu finden. Da wir unser 3D-Modell auf die Satellitenbilder gestützt haben, haben wir uns entschlossen, mit den 13m zu rechnen anstatt mit den 5,1m.

Zuordnung des Themas zu den Nachhaltigkeitszielen der Vereinten Nationen

Literatur

Engel, J. (2009). Anwendungsorientierte Mathematik: Von Daten zur Funktion.: Eine Einführung in die mathematische Modellbildung für Lehramtsstudierende. Springer-Verlag.
Church, J. A., & White, N. J. (2011). Sea-level rise from the late 19th to the early 21st century. Surveys in geophysics, 32(4-5), 585-602.
Rahmstorf, S. (2007). Der Anstieg des Meeresspiegels. Der UN‐Weltklimareport. Bericht über eine aufhaltsame Katastrophe, Köln: Kiepenheuer & Witsch, 190-194.
Meeresspiegelanstieg in Tropischen Inselstaaten
Malediven von Claudia Heidenfelder
Flood map
Lehrpläne
3. Lineare Regression
Wie viel Anbaufläche braucht ein Mensch?