Population der Kirschessigfliege

Modellierungsproblem

Definition Die Kirschessigfliege (Drosophila suzukii) gehört zur großen Gruppe der Tau-, Obst- oder Essigfliegen aus der Familie (Drosophilidae). Die charakteristischen Merkmale sind, dass sie eine Länge von etwa 2–3,5 mm und eine Spannweite von 5–6,5 mm hat. Ihr Körper ist gelb bis braun gefärbt mit dunkleren Streifen auf dem Bauch und sie hat rote Augen. Das Männchen hat einen deutlichen, dunklen Fleck nahe der Spitze jedes Flügels. Die Weibchen haben keine gefleckten Flügel. Das Weibchen hat einen langen, scharfen, gezähnten Eiablageapparat. Mit diesem ritzt es die Früchte auf und legt die Eier hinein.

Kirschessigfliege, Männchen

Modellierungsproblem Die aus Asien stammende Kirschessigfliege (KEF) wurde zunächst in Nordamerika, danach in Europa, erstmals 2009 in Italien, Spanien und Frankreich nachgewiesen. Seitdem rückt sie immer mehr nach Norden vor und wurde im Herbst 2011 auch in Deutschland (Bodensee, Pfalz) und in Belgien nachgewiesen. Das gemäßigte Klima kommt ihr entgegen, optimal sind 20 - 25°C für ihre Aktivität und Vermehrung, sehr warme Temperaturen über 30°C (und somit auch sehr heiße Sommer bei uns) bremsen sie dagegen aus. Sie ist empfindlich gegenüber Trockenheit, mittlere bis hohe Luftfeuchtigkeit sind ihr lieber; zum Überwintern benötigt sie eher milde Temperaturen ab 3°C. Mittlerweile ist sie in ganz Europa zu finden und verursacht durch ihre schnelle Vermehrung enorme Schäden u.a. in Stein- und Beerenobst. Aufgrund des schnellen Entwicklungsverlaufes sind große Populationen möglich, die massiven Schaden verursachen können. Ein Weibchen, das bereits einen Tag nach dem Schlüpfen mit der Eiablage beginnt, kann pro Tag 7 - 16 Eier legen - insgesamt kann es 300 - 400 Eier legen -, und eine einzige Generation der KEF kann innerhalb von 14 Tagen vollendet sein. Die Lebensdauer der KEF schwankt zwischen wenigen Wochen und mehreren Monaten; in Japan entstehen 10 - 15 Generationen der KEF pro Jahr - bei uns ist Schätzungen zufolge eher mit 6-8 Generationen zu rechnen. Verwendet für die Eiablage werden gesunde, reifende Früchte (oftmals nicht lange vor der Ernte, was auch die Verwendung von Insektiziden erschwert), die angeritzt werden - die Kirschessigfliege ist nicht auf beschädigte Früchte angewiesen. Im Jahr 2012 und 2013 wurden erste Schäden vor allem in Brombeeren, Herbsthimbeeren und Holunder nachgewiesen, seit 2013 auch in Trauben. Durch den milden Winter 2013/2014 kam es im Frühjahr 2014 zu einem schnellen Populationsanstieg und erste Befälle in den frühen Süßkirschen wurden bereits Ende Mai (z.B. Burlat, Earlise) festgestellt. Aufgrund günstiger Witterungsbedingungen wurden viele Wirtsfrüchte sehr stark befallen. Schäden traten vor allem in Süß- und Sauerkirschen, Himbeeren, Brombeeren, Zwetschen, Holunder, Aprikosen, Pfirsiche und in Trauben auf. Auch im milden Winter 2014/2015 war die Überlebensrate der überwinternden Population sehr hoch, was durch die Fänge in den Monitoringfallen belegt wurde.

Ziel des Projekts

Da die Kirschessigfliege eine große mögliche Bedrohung für Obst- und Weinbaubetriebe darstellt, ist es zum einen für uns interessant, zu untersuchen, ob wir mit den bisher vorhandenen Daten (aus der Schweiz - allerdings gehen wir davon aus, dass die Lebensbedingungen für die KEF in der Schweiz mit denen in Deutschland vergleichbar sind) Aussagen über das weitere Wachstum der Population und die Vermehrung der KEF in unserem Teil Europas machen können. Ist die KEF ein gefährlicher neueingeschleppter Schädling, oder wird ihre Gefährlichkeit für Obst- und Weinbau überschätzt? Wichtig ist es für uns in diesem Zusammenhang v.a. auch, zu analysieren, wie die Wachstumsrate der KEF im Laufe des Jahres aussieht, wann bzw. in welchen Monaten die Höhepunkte der KEF-Population liegen und wann (zu welchen Zeitpunkten) man dementsprechend am effektivsten zu Gegenmitteln gegen die KEF greifen kann. Eine mit Calc, Geogebra und schließlich Octave entwickelte Modellierung soll hier möglichst gute Auskünfte liefern.

Rohdaten

Beschaffung der Rohdaten: Da die Daten aus Deutschland momentan teilweise gesperrt sind, können diese nur abgeschätzt werden. Deshalb werden wir die Daten aus Schweiz von 2012 bis 2017 verwenden, welches wir auf der Website "Agroscope" gefunden haben. Diese sind vom Standpunkt des Erstauftretens und der Verbreitung der KEF in Europa, sowie den klimatischen Bedingungen her vergleichbar mit der Situation in Deutschland.

Folgende Daten wurden somit ermittelt:

Monat	2012	2013	2014	2015	2016	2017
Januar	0	0	318	24036	7395	175827
Februar	0	0	190	1002	1425	256
März	0	0	575	272	706	3489
April	0	14	635	1428	1232	1647
Mai	3	16	308	1608	1171	489
Juni	32	163	760	1660	6633	5000
Juli	407	1889	22858	23405	80247	28509
August	2396	10166	115521	32450	190133	84373
September	8451	19522	136164	136465	419211	195088
Oktober	33673	17842	346345	170340	232127	180501
November	11840	5000	368708	129729	300732	88371
Dezember	51	80	65955	26603	42057	18223

Modellierungszyklen

Für das Entwickeln unserer Modellierungszyklen verwenden wir die Daten von Agroscope aus der Schweiz. Anhand von Schaubildern wird die Verbreitung der KEF von 2012 bis 2017 deutlich; der Lebenszyklus der KEF kann als exponentielles Wachstum modelliert werden, das Ansteigen der Gesamtpopulation über die Jahre kann durch eine Regressionsgerade gezeigt werden. Durch Ermittlung der durchschnittlichen monatlichen KEF-Population erstellen wir auch die Wachstumsrate, die wir danach mit GeoGebra,Calc/ Excel und schließlich v.a. auch Octave nachzumodellieren versuchen, um ein Modell zu erhalten, das auch aussagekräftig ist. Letztendlich soll es auch Auskunft darüber geben, wie sich die Population der KEF im Jahr verändert, wenn man zu verschiedenen Zeitpunkten (in verschiedenen Monaten) die KEF-Population bekämpft (Zyklus "Spritzen").

Sekundarstufe I: Zyklus 1

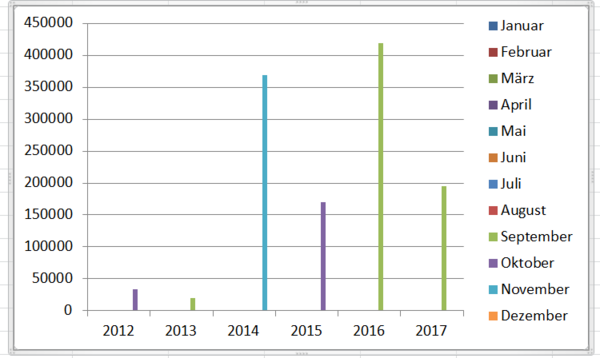
Im ersten Zyklus analysieren wir erhältliche Daten und Schaubilder über die Verbreitung bzw. das manchmal auch massenhafte Auftreten der KEF in Schweiz seit 2012. Die Tabelle und das Diagramm legen nahe, dass die Population der KEF generell jedes Jahr zunimmt, allerdings gab es 2015 im Vergleich mit den anderen Jahren einen leichten Einbruch. Bemerkenswert ist, dass der Sommer 2015 sehr heiß war, was wir später noch genauer betrachten möchten.

Das Maximum der Population über die Jahre hinweg liegt im Spätsommer bzw. im Herbst (vgl. Tabelle 3), also in der Zeit, in der auch die meisten Früchte reif sind.

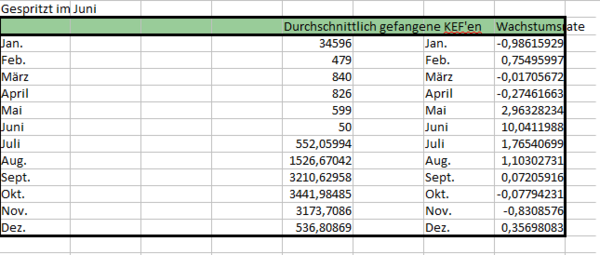
Als nächstes haben wir den Durchschnitt der Anzahl der KEF zwischen den Jahren 2012 bis 2017 berechnet. Dies habe wir, wie folgt, getan: Für die einzelnen Monate haben wir die Anzahl der KEF von 2012 bis 2017 summiert und die erhaltene Summe der gesamten KEF durch die Anzahl der Jahre dividiert.

$DurchschnittMonat={\frac {dj(2012)+dj(2013)+dj(2014)+dj(2015)+dj(2016)+dj(2017)}{6}}$

Monate	Anzahl (gerundet)
Januar	34596
Februar	479
März	840
April	826
Mai	599
Juni	2375
Juli	26219
August	72507
September	152484
Oktober	163471
November	150730
Dezember	25495

Nun haben wir die monatliche Wachstumsrate berechnet:

$Wachstumsrate={\frac {D_{(t)}-D_{(t-1)}}{D_{(t-1)}}}$

Um z.B. die Wachstumsrate in Januar zu erhalten, haben wir :$WachstumsrateJanuar={\frac {DurchschnittswertFebruar-DurchschnittswertJanuar}{DurchschnittswertJanuar}}$ berechnet.

Folgende Wachstumsraten wurden somit ermittelt:

Monate	Wachstumsrate
Januar	-0,99
Februar	0,75
März	-0,02
April	-0,27
Mai	2,96
Juni	10,04
Juli	1,77
August	1,10
September	0,07
Oktober	-0,08
November	-0,83
Dezember	0,36

Sekundarstufe I Zyklus 2

Um die Verbreitung und das gelegentlich massenhafte Auftreten der KEF zu verstehen, ist es auch unerlässlich, sich den Vermehrungszyklus der KEF genauer zu betrachten. Dieser verändert sich; was die Ursachen hierfür sind oder sein könnten - zum Teil sind es, wie bereits oben erwähnt, wohl die klimatischen Bedingungen. Zunächst einmal richten wir unser Interesse auf die warme Jahreszeit (im Winter vermehrt sich die KEF eher nicht, allerdings kann sie unter gewissen Bedingungen - wenn es nicht gar zu kalt wird - überwintern und verlängert dadurch auch ihren Lebenszyklus). Nach Untersuchungen von Kanzawa (1939) leben die KEFS, die im Mai - August auftreten, zwischen 21 und 66 Tagen. Für die Modellierung des Vermehrungszyklus der KEF über eine kurze Zeitspanne hinweg und auf dem Niveau der Sekundarstufe 1 - 2 kann die Sterberate hier daher vernachlässigt werden. Die Vermehrung der KEFs, die vermutlich unter bestimmten Bedingungen langsamer voran geht, ist gut darstellbar durch die Funktion $f(x)=2\cdot 2^{(x-25)}$ bzw. $f(x)=2^{(x-24)}$ (Schaubild Exponentielles Wachstum). Es handelt sich um exponentielles Wachstum: Eine weibliche "langsame" Kirschessigfliege legt 7 Eier pro Tag, von diesen schlüpfen im Durchschnitt nur 50%, also maximal 4 erwachsene KEFs aus. Von diesen ist nur die Hälfte weiblich, und es sind nur die Weibchen, also 2, die wieder neue Eier legen: Daher wird der Funktionswert $2^{(x-25)}$, also Anzahl erwachsener weiblicher Fliegen, mit 2 multipliziert, um die Gesamtstärke der KEF-Population zu zeigen. Der Entwicklungszyklus der "langsamen" KEF dauert ca. 25 Tage, die adulten Tiere schlüpfen also nach 25 Tagen aus und beginnen gleich darauf (einen Tag später) selbst wieder mit dem Eierlegen. Unter für die KEF vermutlich günstigen Bedingungen schafft es die (weibliche) KEF wohl, sogar 16 Eier am Tag zu legen, aus denen die Hälfte KEFs ausschlüpft, also 8, von diesen wiederum sind 4 weiblich und legen weiter. Der Lebenszyklus der KEF kann nach 10 Tagen abgeschlossen sein. Dargestellt ist das durch die Funktion $g(x)=2\cdot 4^{(x-10)}$ (Schaubild Exponentielles Wachstum). Man könnte das exponentielle Wachstum auch mit durchschnittlichen Werten darstellen (Schaubild Vermehrung der KEF im Durchschnitt), Funktion $g(x)=2\cdot 3^{(x-17)}$ ist dafür recht gut geeignet. Deutlich wird, trotz Vernachlässigung der Sterberate, wie rasant schnell sich die KEF unter günstigen Bedingungen vermehren kann.

KEF-Vermehrung, exponentielles Wachstum

Exponentielles Wachstum: Vermehrung der KEF im Durchschnitt

Durch Einsatz von Spritzmitteln gebremste Vermehrung der KEF

Das Versprühen von Insektiziden, die gelegentlich zum Einsatz kommen (meist kurz vor der Ernte, da die KEF ihre Eier vorzugsweise in reife Früchte legt), mag die Population kurzfristig ausbremsen, da sich die KEF aber sehr schnell vermehrt, ist das innerhalb von kurzer Zeit bereits wieder überwunden (Schaubild "Durch Einsatz von Spritzmitteln gebremste Vermehrung der KEF") - es gibt eigentlich kein isoliertes Feld, die KEF kommt sehr schnell vom Feld oder der Wiese nebenan wieder zurück zu dem Platz, an dem sie gerade eben "ausgerottet" worden ist.

Sekundarstufe 2: Zyklus 1

Um eine Vorstellung davon zu erhalten, wie stark sich die KEF in Deutschland bisher vermehrt hat und vielleicht auch weiterhin vermehren wird, kann man sich zunächst einmal die Höhepunkte der KEF-Population genauer betrachten - die Monate September bis November, in denen es die meisten KEF'en gibt.

Höhepunkte der KEF-Population September-November

Höhepunkte KEF-Population September-November Polynom

Beim Versuch, Ordnung bzw ein System in die Anordnung dieser Datenwolke zu bringen, kann man Geogebra verwenden. Dieses liefert beispielsweise ein Polynom 5. Grades:

$p(x)=-0{,}69\cdot x^{5}+12{,}11\cdot x^{4}-79{,}59\cdot x^{3}+241{,}11\cdot x^{2}-326{,}53\cdot x+154{,}13$

p(x) besitzt aber keine wirkliche Aussagekraft - interessant wäre es gewesen, wenn die Realdaten die Extremwerte der Funktion darstellen würden. Aber es ist ledigleich eine Funktion, auf der alle ermittelten Punkte liegen; was dabei dennoch etwas deutlich wird, ist, dass es bisher Minima und Maxima gegeben hat (die aber nicht identisch sind mit den Realdaten, daher kann man p(x) nur mit sehr viel Vorsicht betrachten - und nicht wirklich ernst nehmen auch für die Absicht, eine Entwicklung für die Zukunft abzuschätzen. Hier werden neue Datenpunkte dazukommen und dadurch die Funktion 5. Grades in eine 6., 7.,...n-ten Grades verwandeln... Sie ist also bestenfalls geeignet, das bereits Geschehene andeutungsweise abzubilden.

Zyklus 2

Sinnvoller erscheint es, einen allgemeinen Trend zu suchen:

Höhepunkte Gerade

Geogebra liefert die Regressionsgerade g(x) mit den Residuen $r_{i}$.

ebenso wie Calc

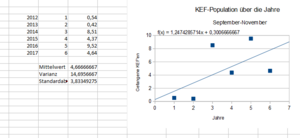
Zunahme der Anzahl der gefangenen KEF'en in den Herbstmonaten September - November über die Jahre 2012 bis 2017 mit Regressionsgerade

$g(x)=1{,}25\cdot x+0{,}3$

(eigentlich, gerundet, $g(x)=125000\cdot x+30000$ ; die Zahlen der gefangenen KEF'en sind jeweils mit $10^{5}$ zu multiplizieren).

${\sqrt {\sum _{i=1}^{n}\mid r_{i}\mid ^{2}}}=6{,}8$

Dass die Schwankungen durch reinen Zufall verursacht werden, ist nicht sehr wahrscheinlich; vermutlich spielen hier solche Faktoren wie das Klima (Temperatur, Luftfeuchtigkeit) eine wichtige Rolle. Die Regressionsgerade g(x) ist so gewählt, dass die Summe der Quadrate der Residuen $r_{i}$ möglichst gering ist. Deutlich wird hier, dass die Anzahl der Kirschessigfliegen jedes Jahr zunimmt; es bleibt abzuwarten, an welche Grenze diese Vermehrung stoßen wird.

Ziel

Im nächsten Zyklus möchten wir die Entwicklung der Population der KEF über die Jahre 2012-2017 analysieren bzw. modellieren.

Vorgehensweise

1. Modellierung der Wachstumsraten mit Geogebra: Verwendung von Schiebereglern

Im ersten Schritt haben wir die ermittelten Wachstumsraten über die Monate in Geogebra in einem Koordinatensystem eingetragen und graphisch dargestellt. Zur Vereinfachung haben wir separat einmal die Punkte von Januar bis Juni und einmal von Juni bis Dezember eingegeben.

Im nächsten Schritt haben wir versucht, mit Hilfe von Schiebereglern, Graphen an die vorhandenen Punkte anzunähern.

$g(x)=0{,}38\cdot x^{3}-3{,}19\cdot x^{2}+8{,}36\cdot x-6{,}44$

${\sqrt {\sum _{i=1}^{n}\mid d_{i}\mid ^{2}}}=0{,}9$

Durchschnittlicher Abstand der Realdaten von der Funktion g(x):

${\frac {\sqrt {\sum _{i=1}^{n}\mid d_{i}\mid ^{2}}}{n}}=0{,}15$

$f(x)=0,58\cdot x^{2}-11{,}68\cdot x+57{,}53$

${\sqrt {\sum _{i=1}^{n}\mid d_{i}\mid ^{2}}}=3{,}31$

Durchschnittlicher Abstand der Realdaten von der Funktion f(x):

${\frac {\sqrt {\sum _{i=1}^{n}\mid d_{i}\mid ^{2}}}{n}}=0{,}47$

Um eine Funktion zu erhalten, die die oben dargestellte Wachstumsrate approximiert, haben wir das Jahr zunächst in zwei Hälften geteilt, weil sich das erste Halbjahr ganz gut als kubische Funktion, das zweite als Parabel annähern lässt, die man dann letztendlich zu einer einzigen Funktion zusammensetzt. Wir haben die vorhandenen Punkte (Monat und zugehörige Wachstumsrate) jeweils in Geogebra eingegeben und dann mit Hilfe von Schiebereglern im ersten Fall die kubische Funktion $g(x)=0{,}38\cdot x^{3}-3{,}19\cdot x^{2}+8{,}36\cdot x-6{,}44$ modelliert als diejenige, die all diesen gegebenen Punkten möglichst nahe kommt, im zweiten Fall die Funktion $f(x)=0,58\cdot x^{2}-11{,}68\cdot x+57{,}53$. Um zu gewährleisten, dass diese beiden Funktionen möglichst dicht an den gegebenen Punkten dran sind, haben wir mit Residuen gearbeitet - hier in unseren Graphen dargestellt als di, der Abstand jeweils zwischen einem Punkt und dem entsprechenden Punkt mit gleichem x-Wert auf unserer Funktion. Ziel war es, ${\sqrt {\sum _{i=1}^{n}\mid d_{i}\mid ^{2}}}$ zu minimieren.

2. Verbindung der beiden Teilfunktionen (mit jeweils eingeschränktem Definitionsbereich

Verbindung der beiden Funktionen

Um beide Funktionen miteinander zu verbinden (Punkt F=(6, 10.04)), müssen sie doch noch ein wenig verändert werden. Für den ersten Teil für $x\in \langle 1,6\rangle$ ist die Funktion

$g(x)=0,38\cdot x^{3}-3,19\cdot x^{2}+8,36\cdot x-7,36$

mit Fehler

${\sqrt {\sum _{i=1}^{6}\mid d_{i}\mid ^{2}}}=1,77$;

für den zweiten Teil für $x\in \langle 6,12\rangle$ ist die Funktion

$f(x)=0,58\cdot x^{2}-11,68\cdot x+59,24$

mit Fehler

${\sqrt {\sum _{i=6}^{12}\mid d_{i}\mid ^{2}}}=5,46$.

Hier war es ausschlaggebend, die beiden Funktionen g(x) und f(x) miteinander zu verbinden in der Darstellung mit Geogebra. Für die Modellierung einer aussagekräftigen Approximation ist dies aber vielleicht nicht der wichtigste Punkt. Möglicherweise kann die Modellierung mit Geogebra auch nicht genau genug werden. Die Arbeit mit Octave liefert hier bessere Ergebnisse.

3. Approximieren der Population der Kirschessigfliegen mit Octave

Die beiden Funktionen der Wachstumsraten wurden gewahlt,

$f(x)=0,5\cdot x^{3}-4,26\cdot x^{2}+10,23\cdot x-10,99$

$g(x)=0,0254\cdot x^{2}-1,000\cdot x+7,396$

da diese nach dem Einsetzen in das Populationmodell mit nichtkonstanter Populationwachstumsrate λ(t), also $p'(t)=\lambda (t)\cdot p(t)$ ein besseres realistisches Ergebniss liefern.

Nämlich, ist die Populationwachstumsrate für das erste halbe Jahr durch die Funktion f(x) bestimmt,

$\lambda _{1}(t)=0,5\cdot t^{3}-4,26\cdot t^{2}+10,23\cdot t-10,99$

gilt nach dem stetigem Wachstumsmodell:

$p'(t)=\lambda _{1}(t)\cdot p(t)$

Dies ist eine gewöhnliche Differentiagleichung erster Ordnung, die man wie folgt lösen kann:

$\Leftrightarrow {\frac {p(t)'}{p(t)}}=\lambda _{1}(t)$

$\Leftrightarrow {\frac {p(t)'}{p(t)}}=0,5\cdot t^{3}-4.26\cdot t^{2}+10,23\cdot t-10,99|\int$

$\Rightarrow (\ln(p(t))=\lbrack {\frac {1}{4}}\cdot 0,5\cdot t^{4}-{\frac {1}{3}}\cdot 4,26\cdot t^{3}+{\frac {1}{2}}\cdot 10,23\cdot t^{2}-10,99\cdot t+c\rbrack$

$\Leftrightarrow p(t)=\mathrm {e} ^{({\frac {1}{4}}\cdot 0,5\cdot t^{4}-{\frac {1}{3}}\cdot 4,26\cdot t^{3}+{\frac {1}{2}}\cdot 10,23\cdot t^{2}-10,99\cdot t+c)}$

$\Leftrightarrow p(t)=\mathrm {e} ^{({\frac {1}{4}}\cdot 0,5\cdot t^{4}-{\frac {1}{3}}\cdot 4,26\cdot t^{3}+{\frac {1}{2}}\cdot 10,23\cdot t^{2}-10,99\cdot t)}\cdot \underbrace {e^{c}} _{={\hat {c}}}$

$\Leftrightarrow p(t)={\hat {c}}\cdot e^{({\frac {1}{4}}\cdot 0,5\cdot t^{4}-{\frac {1}{3}}\cdot 4,26\cdot t^{3}+{\frac {1}{2}}\cdot 10,23\cdot t^{2}-10,99\cdot t)}$

${\hat {c}}$ berechnen :

${\hat {c}}=D_{Januar}\cdot e^{-}{({\frac {1}{4}}\cdot 0,5\cdot t^{4}-{\frac {1}{3}}\cdot 4,26\cdot t^{3}+{\frac {1}{2}}\cdot 10,23\cdot t^{2}-10,99\cdot t)}$

Hierbei ist $t=1$ und D_Januar = 34596 (durchschnittliche Anzahl vom Januar)

${\hat {c}}=34596\cdot e^{-}{({\frac {1}{4}}\cdot 0,5\cdot {1}^{4}-{\frac {1}{3}}\cdot 4,26\cdot {1}^{3}+{\frac {1}{2}}\cdot 10,23\cdot {1}^{2}-10,99\cdot {1})}$

${\hat {c}}=44969423,87861$

Also gilt folgendes Modell für die Populationsentwicklung im ersten Halbjahr:

$p(t)={\hat {c}}\cdot e^{({\frac {1}{4}}\cdot 0,5\cdot t^{4}-{\frac {1}{3}}\cdot 4,26\cdot t^{3}+{\frac {1}{2}}\cdot 10,23\cdot t^{2}-10,99\cdot t)}$

$\Leftrightarrow p(t)=34596\cdot e^{({\frac {1}{4}}\cdot 0,5\cdot t^{4}-{\frac {1}{3}}\cdot 4,26\cdot t^{3}+{\frac {1}{2}}\cdot 10,23\cdot t^{2}-10,99\cdot t)}$

Analog ist die Wachstumsrate im zweiten Halbjahr λ_2(t)=g(t):

$\lambda _{2}(t)=0,0254\cdot t^{2}-1,000\cdot t+7,396$

und nach dem Populationsmodell

$p'(t)=\lambda _{2}(t)\cdot p(t)$

$\Leftrightarrow {\frac {p(t)'}{p(t)}}=\lambda _{2}(t)$

$\Leftrightarrow {\frac {p(t)'}{p(t)}}=0,0254\cdot t^{2}-1,000\cdot t+7,396|\int$

$\Rightarrow (\ln(p(t))=\lbrack {\frac {1}{3}}\cdot 0,0254\cdot t^{3}-{\frac {1}{2}}\cdot 1,000\cdot t^{2}+7,396\cdot t+c\rbrack$

$\Leftrightarrow p(t)=\mathrm {e} ^{({\frac {1}{3}}\cdot 0,0254\cdot t^{3}-{\frac {1}{2}}\cdot 1,000\cdot t^{2}+7,396\cdot t+c)}$

$\Leftrightarrow p(t)=\mathrm {e} ^{({\frac {1}{3}}\cdot 0,0254\cdot t^{3}-{\frac {1}{2}}\cdot 1,000\cdot t^{2}+7,396\cdot t+c)}\cdot \underbrace {e^{c}} _{={\hat {c}}}$

$\Leftrightarrow p(t)={\hat {c}}\cdot e^{({\frac {1}{3}}\cdot 0,0254\cdot t^{3}-{\frac {1}{2}}\cdot 1,000\cdot t^{2}+7,396\cdot t+c)}$

${\hat {c}}$ berechnen :

${\hat {c}}=D_{Juni}\cdot e^{-}{({\frac {1}{3}}\cdot 0,0254\cdot t^{3}-{\frac {1}{2}}\cdot 1,000\cdot t^{2}+7,396\cdot t)}$

Hierbei ist $t=6$ und D_Juni = 2375 (durchschnittliche Anzahl vom Juni)

${\hat {c}}=2375\cdot e^{-}{({\frac {1}{3}}\cdot 0,0254\cdot {6}^{3}-{\frac {1}{2}}\cdot 1,000\cdot {6}^{2}+7,396\cdot {6})}$

${\hat {c}}=0,0000000013381$

Also gilt folgendes Modell für die Populationsentwicklung im zweiten Halbahr:

$p(t)={\hat {c}}\cdot e^{({\frac {1}{3}}\cdot 0,0254\cdot t^{3}-{\frac {1}{2}}\cdot 1,000\cdot t^{2}+7,396\cdot t)}$

$\Leftrightarrow p(t)=0,0000000013381\cdot e^{({\frac {1}{3}}\cdot 0,0254\cdot t^{3}-{\frac {1}{2}}\cdot 1,000\cdot t^{2}+7,396\cdot t)}$

Implementierung/Darstellung dieser Modelle im Octave:

Uni-Niveau: Zyklus 2

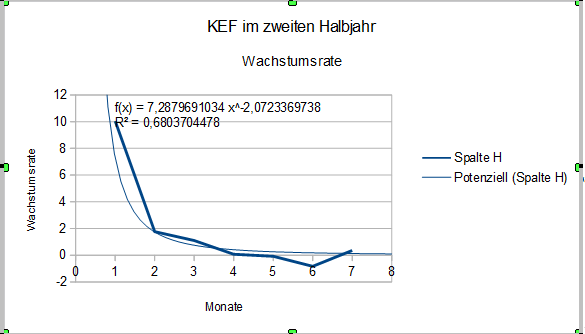
Die vor dem Einsatz von Octave (was schließlich die besten Modellbildungen ermöglicht hat) erarbeiteten Funktionen zur Modellierung des Wachstums in der zweiten Jahreshälfte waren immer noch nicht zufriedenstellend. Wir hatten daher auch anderweitig nach besseren Näherungen gesucht; deutlich wird, dass Octave hier sehr viel besser geeignet ist als Excel, Calc und GeoGebra:

1. OpenOffice Calc liefert die Funktion

$f(x)=7{,}29\cdot x^{-2}-2{,}07\cdot$

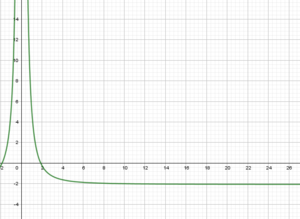
Mit Geogebra wird hier sehr deutlich, dass diese Funktion auch nicht annähernd für die Modellierung der zweiten Jahreshälfte in Frage kommt:

2. Excel liefert die Funktion

$f(x)=0{,}58\cdot x^{2}-5{,}9\cdot x+13{78}$

Diese Funktion ist ebenfalls weit von den Realdaten entfernt:

3. Eine Zusammensetzung aus der Geraden

$h(x)=8{,}26\cdot x+59{,}66$

für $D=(x|6\leq x\leq 7)$ und der Funktion

$j(x)=0{,}19\cdot x^{2}-3{,}88\cdot x+19{,}65$

für $D=(x|7\leq x\leq 12)$ liefert ein recht gutes Modell

In Kombination mit

$g(x)=0{,}38\cdot x^{3}-3{,}19\cdot x^{2}+8{,}36\cdot x-6{,}44$ aus dem ersten Zyklus.

4. Modellieren der Wachstumsfunktion durch Polynom - Interpolation (Lagrange-Polynome)

Vorteil: Alle ermittelten Daten werden von der Funktion abgebildet. Nachteil: Die Funktion suggeriert u.U. auch Entwicklungen, die es tatsächlich nicht gibt.

Interpolation erstes Halbjahr

$p_{1}(x)={\frac {-0,99\cdot (x-2)\cdot (x-3)\cdot (x-4)\cdot (x-5)\cdot (x-6)}{(1-2)\cdot (1-3)\cdot (1-4)\cdot (1-5)\cdot (1-6)}}+{\frac {0,75\cdot (x-1)\cdot (x-3)\cdot (x-4)\cdot (x-5)\cdot (x-6)}{(2-1)\cdot (2-3)\cdot (2-4)\cdot (2-5)\cdot (2-6)}}+{\frac {-0,02\cdot (x-1)\cdot (x-2)\cdot (x-4)\cdot (x-5)\cdot (x-6)}{(3-1)\cdot (3-2)\cdot (3-4)\cdot (3-5)\cdot (3-6)}}+{\frac {-0,27\cdot (x-1)\cdot (x-2)\cdot (x-3)\cdot (x-5)\cdot (x-6)}{(4-1)\cdot (4-2)\cdot (4-3)\cdot (4-5)\cdot (4-6)}}+{\frac {2,96\cdot (x-1)\cdot (x-2)\cdot (x-3)\cdot (x-4)\cdot (x-6)}{(5-1)\cdot (5-2)\cdot (5-3)\cdot (5-4)\cdot (5-6)}}+{\frac {10,04\cdot (x-1)\cdot (x-2)\cdot (x-3)\cdot (x-4)\cdot (x-5)}{(6-1)\cdot (6-2)\cdot (6-3)\cdot (6-4)\cdot (6-5)}}$

bzw.

$p_{1}(x)=-0,021\cdot x^{5}+0,3121\cdot x^{4}-1,2508\cdot x^{3}+0,3379\cdot x^{2}+5,4518\cdot x-5,82$

Interpolation zweites Halbjahr

$p_{2}(x)={\frac {10,04\cdot (x-7)\cdot (x-8)\cdot (x-9)\cdot (x-10)\cdot (x-11)\cdot (x-12)}{(6-7)\cdot (6-8)\cdot (6-9)\cdot (6-10)\cdot (6-11)\cdot (6-12)}}+{\frac {1,77\cdot (x-6)\cdot (x-8)\cdot (x-9)\cdot (x-10)\cdot (x-11)\cdot (x-12)}{(7-6)\cdot (7-8)\cdot (7-9)\cdot (7-10)\cdot (7-11)\cdot (7-12)}}+{\frac {1,1\cdot (x-6)\cdot (x-7)\cdot (x-9)\cdot (x-10)\cdot (x-11)\cdot (x-12)}{(8-6)\cdot (8-7)\cdot (8-9)\cdot (8-10)\cdot (8-11)\cdot (8-12)}}+{\frac {0,07\cdot (x-6)\cdot (x-7)\cdot (x-8)\cdot (x-10)\cdot (x-11)\cdot (x-12)}{(9-6)\cdot (9-7)\cdot (9-8)\cdot (9-10)\cdot (9-11)\cdot (9-12)}}+{\frac {-0,08\cdot (x-6)\cdot (x-7)\cdot (x-8)\cdot (x-9)\cdot (x-11)\cdot (x-12)}{(10-6)\cdot (10-7)\cdot (10-8)\cdot (10-9)\cdot (10-11)\cdot (10-12)}}+{\frac {-0,83\cdot (x-6)\cdot (x-7)\cdot (x-8)\cdot (x-9)\cdot (x-10)\cdot (x-12)}{(11-6)\cdot (11-7)\cdot (11-8)\cdot (11-9)\cdot (11-10)\cdot (11-12)}}+{\frac {0,36\cdot (x-6)\cdot (x-7)\cdot (x-8)\cdot (x-9)\cdot (x-10)\cdot (x-11)}{(12-6)\cdot (12-7)\cdot (12-8)\cdot (12-9)\cdot (12-10)\cdot (12-11)}}$

Zusammengesetzte Wachstumsfunktion über das ganze Jahr

$f(x)=p_{1}(x)+p_{2}(x)$

Uni-Niveau: Zyklus 3

Spritzmitteleinsatz gegen die KEF in verschiedenen Monaten

("Spritzmitteleinsatz" wollen wir hier ganz allgemein als "Maßnahmen der Bekämpfung und Reduktion der Schädlinge" verstehen; in der Praxis könnte es vielleicht manchmal tatsächlich sinnvoller sein, beispielsweise engmaschige Netze über Obstbestände zu spannen - was ja auch gemacht wird, obwohl es vermutlich arbeitsintensiv ist - statt womöglich nur hochgiftige Insektizide zu versprühen, die nicht einmal unbedingt verhindern, dass sehr bald die KEF aus Hecken, Wiesen und Feldern neben dem gerade gespritzten Feld in dasselbe wieder zurückkehren. Wichtig ist für uns hier aber der Zeitpunkt des Einsatzes.)

In unserer Modellierung erscheint die Schädlingsbekämpfung in den Monaten Juni und Juli am effektivsten.

Die Wachstumsrate sei λ. Dann berechnet sich der KEF-Bestand b(t) für jeden Monat wie folgt (vgl. Lehrplan für Klasse 10):

$b(t)=b(t-1)\cdot (1+\lambda _{t-1})$

Zum Beispiel ergibt sich im nachfolgenden ersten Beispiel (Spritzmitteleinsatz gegen KEF im April) für $b(Mai)=b(April)\cdot (1+\lambda _{April})$ bzw.

$b(5)=b(4)\cdot (1+\lambda _{4})$ folgende Berechnung:

$b(5)=50\cdot (1-0,27)$ mit dem Ergebnis b(5)=36 (gerundet auf ganze KEF'en).

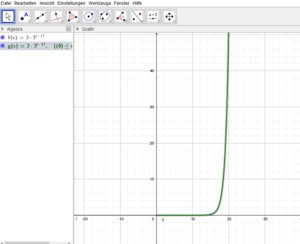
Nun haben wir dies auch in Octave durchgeführt und folgende mathematische Resultate ermittelt, hier am Beispiel für "Spritzen im Juni", da dies als zeitlich sehr effektives "Spritzen" erscheint:

Der dazugehörige Skript:

Graph zum Einsatz von Spritzmitteln im Juni:

Niveauzuordnung

Sekundarstufe 1:

• Recherche von Informationen und Daten (Internet und Kontaktaufnahme zu wissenschaftlichen Einrichtungen)
• Daten aus Texten auswerten, Diagramme verstehen
• Erstellung von Tabellen und Diagrammen
• Modellieren von exponentiellem Wachstum
• Software: OpenOffice Calc, Geogebra

Sekundarstufe 2:

• Modellieren von exponentiellem Wachstum
• Software: OpenOffice Calc, GeoGebra

Universität:

• Lineare/nichtlineare Regression
• Populationsberechnung
• Populationsmodelle mit nichtkonstanter Populationswachstumsrate, Differentialgleichung

Software: Geogebra, Octave

Literaturangaben

• https://drosophila.julius-kuehn.de/index.php?menuid=3
• https://www.cabdirect.org/cabdirect/abstract/19410501073
• Daten von Agroscope: Synthese_2017 (XLS, 747 kB, 22.10.2018)

https://www.agroscope.admin.ch/agroscope/de/home/themen/pflanzenbau/pflanzenschutz/www.drosophilasuzukii.agroscope.ch/drosophila_suzukii_monitoring_piegage.html