Schadstoffausbreitung in einem Gewässer

Thema und Zielsetzung

Nitrate im Trinkwasser gelten ab einer Konzentration von 50 mg/l als bedenklich für den Menschen.[1] Dieser Grenzwert wird in Deutschland häufig überschritten. Dementsprechend beschäftigen wir uns mit der Frage, wie schnell sich Nitrat in einem See ausbreitet und in welcher Konzentration es an einem Ort, zu einem bestimmten Zeitpunkt vorliegt.

Modellierungszyklen

Modellierungszyklus 1

Zielsetzung

Berechnung der Zeitdauer, die der Schadstoff braucht, um an einen bestimmten Punkt im See zu gelangen und die Konzentration des Schadstoffs an diesem Punkt. Hierzu nehmen wir an, dass sich der Schadstoff linear in zwei Dimensionen ausbreitet und äußere Einflüsse, wie Strömungen und Diffusion keinen Einfluss haben.

Fragestellungen

1. Wann ist der Schadstoff an einem bestimmten Punkt im See angekommen?

2. Wie hoch ist die Konzentration zu diesem Zeitpunkt an diesem Punkt?

Annahmen

1. Der Schadstoff breitet sich linear aus.

2. An jedem Punkt, an dem der Schadstoff angekommen ist, ist die Konzentration gleich hoch.

Verwendete Software

Geogebra

Durchlauf 1

Vorgaben

Seemaße: 100x1000m

Austrittsort: 50x0m

Austrittsmenge: 1000gr

Ausbreitungsgeschwindigkeit: 1m/s

Um die Frage, wann der Schadstoff an welchem Punkt im See angekommen ist, zu beantworten, erstellen wir eine Funktion in Abhängigkeit von der Länge des Sees (x) und der Zeit seit dem Austritt des Schadstoffs (t). T wird als Schieberegler, mit einer Spanne von 0 bis 1200, angelegt, wobei jeder Schritt für eine Sekunde steht. Der Ursprung wird als Austrittsort festgelegt. Mithilfe des Satzes von Pythagoras lässt sich nun die passende Breite in Abhängigkeit von x und t berechnen. X darf hierbei nicht größer als 1000 werden, da der See nur die Länge von 1000 Meter hat.

$f(x,t)=Wenn(0\leq x\leq 1000,\surd (t^{2}-x^{2})$

Diese Funktion darf nur eingeblendet werden, wenn der y-Wert kleiner oder gleich 50 ist

$g(x)=Wenn(f(x)\leq 50,f(x))$

und g(x) muss an der x-Achse gespiegelt werden, sodass die Ausbreitung im kompletten See sichtbar wird.

$h(x)=Wenn(-f(x)\geq -50,-f(x))$

Für die Darstellung muss f(x) ausgeblendet werden und die Farben von g(x) und h(x) angepasst werden (s. Abb.1).

Um die Konzentration an den Punkten zu ermitteln, nutzen wir die Formel:

c(x)= 1000/bedeckte Fläche

Hierfür muss noch die bedeckte Fläche in Abhängigkeit von der Zeit ermittelt werden. Es wird ein identischer Schieberegler wie zur Beantwortung der ersten Frage implementiert. Wir nehmen eine Fallunterscheidung vor.

1. Fall t≤50

Berechnung des Flächeninhalts eines Halbkreises:

$i(x)=(pi\cdot t^{2})\div 2$

2. Fall t>50

Berechnung des Flächeninhalts eines Rechtecks mit der Breite 100 und der Länge t-50 plus den Flächeninhalts des Halbkreises mit dem Radius 50:

$j(x)=50\cdot pi+(t-50)\cdot 100$

Diese beiden Formeln müssen noch mit einer Wenn-Aussage verbunden werden, sodass das Programm entscheidet welche zutrifft, und demnach die richtige Konzentration berechnet.

$o(x)=Wenn(t\leq 50,i(x),j(x))$

Im Anschluss lässt sich c(x) definieren als:

$c(x)={\frac {1000}{o(x)}}$

Als letztes wird o(x) als bedeckte Fläche und c(x) als Konzentration benannt und alle anderen Funktionen ausgeblendet (s. Abb.2).

Durchlauf 2

Im zweiten Durchlauf gelten alle Vorgaben wie im ersten, nur dass man die Ausbreitungsgeschwindigkeit individuell anpassen kann.

Hierzu wird eine Variable a definiert, die zwar von t abhängig ist, deren Definition dem Sachverhalt aber angepasst werden kann. In unserem Durchlauf haben wir a definiert als:

$a=1,9\cdot 10^{-3}\cdot t$

Durch die drastische Verkleinerung der Zeitschritte muss der Schieberegler deutliche mehr Zeitschritte enthalten. Dementsprechend wurde er angepasst und läuft nun 10 hoch 5 Zeitschritte ab.

Dementsprechend lassen sich die Folien aus Durchlauf 1 anpassen, indem in den Formeln jedes t durch ein a ersetzt wird. Dies ist in den zwei Abbildungen (Abb.3 und Abb.4) zu sehen. Der Vorteil hierbei ist, dass der Schieberegler nur noch die Anzahl der Zeitschritte vorgibt, aber nicht mehr deren Länge.

Probleme

Die Probleme des ersten Zyklus liegen bereits in den beiden Annahmen. Ein Stoff breitet sich weder linear aus, noch liegt an jedem Punkt dieselbe Konzentration vor. Diese beiden Annahmen wurden getroffen, um eine Reduktion vorzunehmen und eine Bearbeitung des Themas in Sekundarstufe I zu ermöglichen. Es ist wahrscheinlicher, dass die Konzentration am Austrittsort am höchsten ist und sich mit zunehmender Entfernung verringert. Demnach könnte eine Normalverteilung mit dem Austrittsort als Erwartungswert vorliegen. Diese Annahme liegt dem zweiten Zyklus zugrunde, allerdings beschäftigt sich dieser Zyklus mit der Modellierung im 1-dimensionalem Raum.

Modellierungszyklus 2

Fragestellung:

Wie hoch ist die Konzentration eines Schadstoffs an einem bestimmten Punkt, nach einer bestimmten Zeit, in einem eindimensionalen Raum?

Annahme:

Der Schadstoff breitet sich durch einen Diffusionsprozess aus. Da die Diffusionsgleichung mit den Mitteln der Sekundarstufe weder herleitbar noch lösbar ist, wird in diesem Zyklus die Fundamentallösung als gegeben angesehen. Diese lautet:

(Parameter a in die untere Formel ergänzen)

$c(x,t)={\frac {1}{\sqrt {4\cdot pi\cdot t}}}\cdot e^{\frac {-(x-u)^{2}}{4\cdot t}}$

Vorgaben:

- t= Zeitangabe in Sekunden

- x= Breitenwert des Stabs

- u= Austrittsort= 50

- Austrittsgeschwindigkeit= 1 m/s

- b= c(x)*100 vorliegende Konzentration an einem bestimmen Punkt

Mit diesen Vorgaben und der Gleichung kann die Konzentration an jedem einzelnen Punkt berechnet werden. Hierfür muss ein Wert für c(x) in b eingesetzt werden (s. Abb.5).

Im nächsten Durchlauf sollen Austrittsort und Ausbreitungsgeschwindigkeit individuell anpassbar gemacht werden. Hierfür wird der feste Wert für u durch einen Schieberegler ersetzt und die Variable a implementiert (s. Abb. 6).

$a=d\cdot t$

In unserem Beispiel ist $d=1,9\cdot 10^{-3}$ .

Probleme:

Modell simuliert ein Problem im eindimensionalen Raum und lässt sich nicht einfach auf den zweidimensionalen Raum übertragen. Es ist keine genaue Berechnung möglich.

Alternativen

Genaue Berechnung des Diffusionsprozesses mithilfe der LaPlace-Matrix.

Diese alternative wird in Zyklus 3 modelliert.

Modellierungszyklus 3

Mithilfe der eindimensionalen Diffusion wird in drei Durchläufen, in denen verschiedene Verfeinerungen vorgenommen werden, die numerische Modellierung mit der Software Octave durtchgeführt. Für die Herleitung der genutzten Formel siehe Finite-Differenzen-Methode, siehe auch Räumliche Diffusion.

(Hier noch ausführlich die Zeitdiskretisierung / Zeitschleife beschreiben)

Durchlauf 1

Zielsetzung:

Berechnung der Zeitdauer, die der Schadstoff braucht, um an einen bestimmten Punkt im See zu gelangen und die jeweils neue Konzentration des Schadstoffs an diesem Punkt.

Durchführung:

Um dies zu beschreiben haben wir uns in Octave die Diffusion 1D, also im eindimensionalen Raum zur Veranschaulichung herangezogen. Dazu sind wir wie folgt vorgegangen. Die Startparameter sind als fest gewählt und der Einfachheit halber wählen wir Δ t =Δ x=1. Die einzelnen Konzentrationen werden für jeden Zeitschritt in einem Array C gespeichert. Anschließend wird eine erste Darstellung der Konzentration in Abhängigkeit von Weg x und Zeit t angezeigt. Die Startparameter sind zu Beginn wie in Abb.1 gezeigt, festgelegt worden.

Weiterhin wird die Anfangskonzentration c0 festgesetzt. Nun folgt eine Arbeitsschleife, die die neue Konzentration in Abhängigkeit der Startparameter berechnet. Durch C=[C,x] wird die neue Konzentration in den C-Array abgespeichert. Zuletzt wird ein dreidimensionales Koordinatensystem geplottet, wobei die X-Achse die Zeit, die Y- Achse der Weg und die Z-Achse die Konzentration in Abhängigkeit von Weg und Zeit darstellt.

Durchlauf 2

Im nächsten Durchlauf wird die Schrittweite verfeinert, indem zum einen für die Schrittweite Δ x und den Zeitschritt Δ t kleinere Werte angenommen werden und zum anderen eine 2D-Darstellung für verschiedene Zeitpunkte t implementiert wird.

Zielsetzung:

Ebenso wie in Durchlauf 1 berechnen wir die Zeitdauer, die der Schadstoff braucht, um an einen bestimmten Punkt im See zu gelangen und die neue Konzentration des Schadstoffs an diesem Punkt. Allerdings nehmen wir nun eine erste Verfeinerung der nummerischen Berechnung vor, sodass die Schrittweite von x und t beliebig angepasst werden kann. Ausgegeben wird ein Diagramm c(x), welches aber feste Zeitpunkte t vorgibt.

Durchführung:

Wie in Durchlauf 1 legen wir zu Beginn wieder die Startvariablen fest, die in Abb.2 dargestellt sind. Insbesondere soll für die Konstante k gelten: $k={\frac {\Delta t}{\Delta x^{2}}}$

Datei:Abb.3 FOR-Schleife zur Berechnung der neuen Konzentration v1.1.png

Abb.3 FOR-Schleife zur Berchnung der neuen Konzentration v1.1

Die Arbeitsschleife, die wie in Abb.3 aufgebaut ist, soll dazu dienen, die Konzentration neu zu berechnen

Nach Beendigung der Schleife gibt uns Octave ein, wie unten zu sehen, zweidimensionales Koordinatensystem aus, das auf der X-Achse den Weg und auf der Y-Achse die Konzentration angibt. Die Ausgabe gibt hier vier Kurven an, die die Ausbreitung des Schadstoffes in Abhängigkeit der Konzentration und der Zeit darstellen. Die Zeitpunkte wurden vorher fest gewählt.

Durchlauf 3

Zielsetzung:

Ebenso wie in Durchlauf 1 und 2 berechnen wir die Zeitdauer, die der Schadstoff braucht, um an einen bestimmten Punkt im See zu gelangen und die Konzentration des Schadstoffs an diesem Punkt. Im letzten Durchlauf wird die Neumansche Randbedingung implementiert. Außerdem wird die Abspeicherung im C-Array innerhalb der Arbeitsschleife angepasst, da bei großen Datenmengen die Rechenleistung zu stark beansprucht wird. Die grafische Ausgabe wird weiter verfeinert, indem die abgebildeten Zeitpunkte beschriftet werden und von den Startvariablen abhängen.

Durchführung:

Zu Allererst setzen wir alle Variablen zurück und starten den Timer um am Ende zu sehen, wie lange die Berechnung der Werte gedauert hat. Dies ist deshalb wichtig, da bei zu groß gewählter Zeitspanne die Rechenleistung womöglich nicht ausreicht und sich somit das Programm aufhängt.

Nun legen wir, wie schon in den beiden Durchläufen zuvor die Startvariablen, wie in Abbildung 4 fest.

Die Konstante $k={\frac {\Delta t}{\Delta x^{2}}}$ bleibt wie im zweiten Durchlauf bestehen. Weiterhin werden, wie im vorherigen Durchlauf die Vektoren, die Anzahl der Konzentrationswerte, sowie die Anzahl der Zeitpunkte und zusätzlich ein Zeitarray für den Plot definiert. Ebenso wir die Anfangskonzentration r festgelegt und die Neumansche Randbedingungen hinzugefügt(Abb.5).

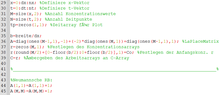
Die Arbeitsschleife berechnet nun unter Berücksichtigung der Neumanschen Randbedingungen und der eventuellen hohen Rechenanforderung die Konzentration des Schadstoffes neu und speichert diese ab. Siehe dazu Abbildung 6

Nun wird wie im Bild unten zu sehen, die verfeinerte Darstellung der Konzentration zu selbst ausgewählten Zeitpunkten ausgegeben.

Modellierungszyklus 4

Im folgenden Zyklus wird der zweidimensionale Diffusionsprozess mithilfe der numerischen Diskretisierung in Software Octave modelliert.

Vorüberlegungen:

Analog zum eindimensionalen Fall wird die Differentialgleichung (Difussionsgleichung) ${\frac {\partial c({\overrightarrow {x}},t)}{\partial t}}=D\cdot \Delta c({\overrightarrow {x}},t)$ mit Hilfe der Finite-Differenzen-Methode gelöst, um die Konzentrationswerte $c(x,y,t+\Delta t)$ numerisch zu bestimmen. Im zweidimensionalen Raum gilt für den Laplace-Operator: $\Delta ={\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}$ . Damit folgt für die Differentialgleichung der Diffusion:

${\frac {\partial c(x,y,t)}{\partial t}}=D\cdot \left({\frac {\partial ^{2}c(x,y,t)}{\partial x^{2}}}+{\frac {\partial ^{2}c(x,y,t)}{\partial y^{2}}}\right)$

Durch Approximierung der Differentialquotienten folgt:

${\frac {c(x,y,t+\Delta t)-c(x,y,t)}{\Delta t}}=D\cdot \left({\frac {c(x-\Delta x,y,t)-2\cdot c(x,y,t)+c(x+\Delta x,y,t)}{\Delta x^{2}}}+{\frac {c(x,y-\Delta y,t)-2\cdot c(x,y,t)+c(x,y+\Delta y,t)}{\Delta y^{2}}}\right)$

Auflösen nach $c(x,y,t+\Delta t)$ und die Annahme, dass $\Delta x=\Delta y=h$ gilt, führen zur Ausgangsgleichung, durch welche die neuen Konzentrationswerte berechnet werden können:

$c(x,y,t+\Delta t)=c(x,y,t)+D\cdot k\cdot \left[c(x-\Delta x,y,t)+c(x,y-\Delta y,t)-4\cdot c(x,y,t)+c(x+\Delta x,y,t)+c(x,y+\Delta y,t)\right]$ ,

wobei $k={\frac {\Delta t}{h}}$ entspricht.

Aufgrund der endlichen betrachteten Fläche müssen Vorkehrungen an den Rändern getroffen werden, da beispielsweise am linken Rand ein Konzentrationswert $c(x-\Delta x,y,t)$ nicht existiert. Dazu wird in den ersten Modellierungsdurchläufen feste Randwerte vom Betrag 0 angenommen. Im weiteren Verlauf sollen sie dann durch Neumann'sche Randbedingungen ersetzt werden, wobei für diese dann (beispielhaft für den rechten Rand) gilt:

$c(x+\Delta {x},y,t)=c(x,y,t)+N\cdot \Delta x$ , wobei N eine Konstante darstellt, die für jeden Rand frei wählbar ist.

Durchlauf 1

Zielsetzung:

Die Differentialgleichung der Diffusion soll durch die finite Differenzen-Methode gelöst werden. Anschließend wird für feste Zeitschritte delta_t das Konzentrationsprofil in Abhängigkeit des Ortes bei gegebener Anfangskonzentration numerisch berechnet und abschließend grafisch dargestellt.

Durchführung:

Im ersten Durchlauf soll ein erster Lösungsansatz der 2D-Diffusions-Differentialgleichung in Octave implementiert werden. Dazu wird von einem festen Zeit- und Wegschritt $\Delta t$ bzw. $\Delta x$ und $\Delta y$ von 1 ausgegangen, wodurch sich für $k={\frac {\Delta t}{\Delta x^{2}}}={\frac {\Delta t}{\Delta y^{2}}}=1$ ergibt. Um fehlerhafte Berechnungen zu vermeiden, werden die Randpunkte des betrachteten Gebietes 0 gesetzt und nur innerhalb dieses Randes neue Konzentrationswerte berechnet.

Nachdem eine Startkonzentration $C_{0}$ in der Mitte des betrachteten Gebietes für einen Ortspunkt, sowie die Startparameter, wie in Abb. 1 dargestellt, festgelegt wurden, wird die Berechnung neuer Konzentrationswerte nach der Zeitdauer $\Delta t$ durch eine FOR-Schleife realisiert. Innerhalb dieser Zeitschleife wird jeweils für jeden Raumpunkt die neue Konzentration in Abhängigkeit der umliegenden Konzentrationswerte berechnet, was durch zwei weiteren FOR-Schleifen umgesetzt wird (siehe Abb. 2).

Abschließend wird nach abgeschlossener Berechnungen nach der betrachteten Zeitdauer nt das Konzentrationsprofil grafisch durch den Befehl surf ausgegeben, wie in Abb. 3 exemplarisch dargestellt.

Da die Konzentrationswerte für vergleichsweise große Wegschritte berechnet wurden, ist der Übergang von einer Konzentration zur benachbarten zu ungenau, weshalb im nächsten Durchlauf eine Verfeinerung der Schrittweite $\Delta x$ und $\Delta y$ vorgenommen wird.

Abb. 3: Grafische Darstellung der Modellierung der 2D-Diffusion v1.0

Durchlauf 2

Zielsetzung:

Aufgrund der Tatsache, dass im ersten Durchlauf der Abstand zwischen den einzelnen Raumpunkten als 1 angenommen wurde und damit einhergehend eine nur grobe Annäherung des Diffusionsprozess umgesetzt werden konnte, wird im folgenden Durchlauf sowohl eine feinere Schrittweite $\Delta x$ bzw. $\Delta y$ , als auch einen kleineren Zeitschritt delta_t implementiert.

Durchführung:

Auf Grundlage des ersten Durchlaufs wird der Programmcode dahingehend erweitert, dass die Schrittlänge $\Delta x$ und $\Delta y$ frei wählbar sind (siehe Abb. 4).

Dies bedingt, dass die inneren FOR-Schleifen um den Faktor ${\frac {1}{\Delta x}}\cdot {\frac {1}{\Delta y}}$ mehr Berechnungen als im 1. Durchlauf durchführen müssen und somit deren Anweisungen leicht modizifiziert werden müssen (Abb. 5).

Ebenfalls kann der Zeitschritt ebenfalls frei gewählt werden, wodurch sich noch genauere Konzentrationswerte für die einzelnen Raumpunkte berechnen lassen. Im Vergleich zum ersten Durchgang konnte der Übergang zwischen den einzelnen Raumpunkten genauer berechnet werden, wie ein Vergleich der Abb. 6 mit der Abb. 3 deutlich zeigt, wodurch davon ausgegangen werden kann, dass der Diffusionsprozess genauer angenähert werden konnte.

Bei der grafischen Darstellung sind jedoch die Achsen zum einen noch unbeschriftet und zum anderen falsch skalliert, was in der nächsten Durchführung noch weiter angepasst werden soll. Außerdem ist die Färbung der „Konzentrationsfläche“ fehlerhaft, was zu falschen Schlüssen führen könnte.

Abb. 6: Grafische Darstellung der Modellierung der 2D-Diffusion v1.1

Durchlauf 3

Zielsetzung:

Wie bereits vorher beschrieben, soll nun die grafische Ausgabe verbessert werden. Außerdem soll die Wahl der Startkonzentration weiter angepasst werden, wodurch nicht mehr nur von einer Konzentration in einem Raumpunkt, sondern von einem vorgegeben Konzentrationsband ausgegangen werden soll.

Durchführung:

Wie bereits am Ende des 2. Durchgangs geschildert, war die Achseneinteilung fehlerhaft bzw. falsch dimensioniert, was nun durch eine separate Definition von x- und y-Arrays angepasst wird. Außerdem wurde die Beschriftung der grafischen Darstellung so angepasst, dass der Diffusionskoeffizient sowie die Dimension der Achsen angezeigt wird (Abb. 7).

Im Gegensatz zu den vorhergehenden Durchgängen wurde die grafische Ausgabe über den Befehl mesh vorgezogen, da somit keine Flächen, sondern ein Drahtgittermodell des Konzentrationsprofils ausgegeben wird, dessen farbliche Darstellung keine verfälschten Schlüsse zulässt.

Die Anfangskonzentration erstreckt sich nun über einen vorher definierten Raumbereich statt sich nur auf einen Raumpunkt zu konzentrieren, was der Realität näher kommt. Eine weitere Anpassung dieses Startparameters soll im letzten Durchlauf weiter verfeinert werden, sodass eine Startbreite und -länge frei wählbar ist. Des weiteren sollen die Randpunkte dahingehend überarbeitet werden, dass die Randkonzentration nun nicht mehr konstant null, sondern von der Differenz zur Nachbarkonzentration abhängen (Riemann’sche Randbedingungen).

Abb. 8: Grafische Darstellung der Modellierung der 2D-Diffusion v1.2

Durchlauf 4

Zielsetzung:

Um den Modellierungsprozess abzuschließen, wird nun eine freiwählbare Anfangskonzentration in den Programmcode implementiert, wodurch die Startparameter noch genauer definiert werden können. Zusätzlich werden Riemann’sche Randbedingungen eingefügt, was zur Folge hat, dass die Randpunkte nicht mehr als konzentrationslos angesehen werden müssen.

Abb. 9: Festlegung der Startkonzentration v1.3

Durchführung:

Wie in Abb. 9 dargestellt, lässt sich nun durch Eingabe einer Breite und einer Länge die Größe der Fläche der Startkonzentration frei wählen.

Da bei gerader Anzahl an x- bzw. y-Werten eine genaue Lokalisierung der Mitte nicht möglich ist, wird dies nicht für alle Startparameter garantiert. Anschließend werden die Randwerte durch Neumann’sche Randbedingungen festgelegt, indem die räumliche Änderung der Konzentration 0 gesetzt wird. Durch diese Anpassung kann die betrachtete Fläche im Vergleich zu den vorherigen Durchläufen verkleinert werden, wobei die Berechnung der neuen Konzentrationswerte auf das Gebiet ohne die Randwerte beschränkt bleibt.

Sobald die FOR-Schleife den letzten Punkt des inneren Gebietes berechnet hat, werden alle Randwerte durch die Neumann’schen Randbedingungen neu festgelegt (vergleiche Abb. 10). Abschließend erfolgt die Ausgabe des Konzentrationprofils in einem 3D-Drahtmodell (siehe Abb. 11).

Abb. 11: Grafische Darstellung der Modellierung der 2D-Diffusion v1.3

Niveauzuordnung

Sekundarstufe I

Satz des Pythagoras
Lineare Funktion
Flächeninhaltsberechnung (Kreis/Rechteck)

Sekundarstufe 2

Universität

Softwarenutzung

Nachhaltigkeitsziele

SDG 3: Good Health and Well-being
- Durch die Verschmutzung des Gewässers kann es zu erheblichen Gesundheitsrisiken kommen. Das Wissen über die mögliche Ausbreitung hilft dabei die Risiken einzuschätzen und zu verringern.

SDG 6: Clean Water and Sanitation
- Das Wasser des Sees gelangt durch die Erdschichten ins Grundwasser und daurch ins Trinkwasser der umliegenden Gebiete. Dementsprechend wird nicht nur der See, sondern auch das Trinkwasser verunreinigt. Das Wissen um den Grad der Verschmutzung kann bei einer effektiven Bekämpfung helfen.
SDG 13: Climate Action
- Die Verschmutzung des Wassers fördert den Klimawandel und das erhöhte Vorkommen extremer Wetterereignisse.
SDG 14: Life Below Water
- Der Schadstoff hat eine direkte Auswirkung auf das Leben im See. Um geeignete Maßnahmen zur Wiederherstellung der normalen Bedingungen ergreifen zu können, muss das Ausmaß der Katastrophe bekannt sein.

Alternativen

Neben den mathematischen Alternativen, die wir in den unterschiedlichen Zyklen behandelt haben, indem wir von unterschiedlichen Vorgaben ausgegangen sind und unterschiedliche herangehensweisen ausprobiert haben, könnte man das Modell der realen Situation annähern. Möglichkeiten hierfür wären die Annahme einer Strömung und die Verwendung der Konvektions-Diffusions-Gleichung, die Annahme eines stetigen Schadstoffaustritts und dem Implementieren einer Quellfunktion oder die Annahme einer anderen Seeform mit Hindernissen im Inneren des Sees.

Literatur

Dieses Thema wird bearbeitet von: Kevin Müller, Raphael Schmidt, Günter Rink