Streuung von Spritzmitteln

Hier entsteht ein Portfolio zur Mathematischen Modellbildung zum Thema Streuung von Spritzmitteln.

Ziel des Projekts

Ziel ist es, anhand der äußeren Voraussetzungen (z.B. der Nähe zu benachbarten Feldern, Windrichtung und -stärke) zu berechnen, wie Pflanzenschutzmittel (kurz PSM) auf den eigenen Anbauflächen gespritzt werden können, sodass dies sich nicht auf andere (eventuell unbehandelte) Agrargebiete auswirkt.

Softwarenutzung

• GeoGebra

Zuordnung zu den Nachhaltigkeitszielen

SDG 3: Good Health and Well-being

SDG 9: Industry, Innovation and Infrastructure

SDG 15: Life on Land

Modellierungszyklus 1

Zielsetzung

Erstellung eines anschaulichen, dynamischen Modells in GeoGebra, dass die Ausbreitung eines Spritzmittels, von einem sich bewegenden Träger veranschaulicht und mithilfe dessen, man die Sprühkonzentration an einem Punkt/ zu einem Zeitpunkt berechnen kann.

Annahmen

1. Das Spritzmittel breitet sich von stationären Quellen auf dem Weg aus.

2. Die Ausbreitung ist gleichmäßig, kreisförmig.

3. Innerhalb eines Ausbreitungskreises, ist die Spritzmittelkonzentration an jedem Punkt gleich.

Durchführung

Ausgangspunkt für die Modellierung in GeoGebra, ist die Erstellung eines Fahrweges, den die Funktion später nehmen soll und welcher in GeoGebra eine Gesamtlänge von 1 zugewiesen wird. Dies ist wichtig für die spätere Anwendung von Pfadparametern.

$Wingert=Spline[ListevonPunkten]$

Weiter werden zwei Schieberegler $tDyn=(0,3)$und $t=(0.1+tDyn)$ angelegt, jeweils mit einer Schrittweite von 0,001, dies soll hier einer Sekunde entsprechen. t wird weiter mit einem Schalter für das An- und Ausschalten der Animation versehen.

Für die Konstruktion der stationären Quellen entlang des Wingerts, in Abhängigkeit von der Zeit, erstellen wir nun eine Liste mit Pfadparametern. Dazu wird ein weiterer Schieberegler benötigt, der für die Anzahl der Quellen, die auf dem Weg gleichmäßig „ausgelegt“ werden sollen, steht. Als sinnvoll erwies sich für unser Modell der Bereich

$SpruehHaeufigkeit=(50,100)$.

Die Liste für die Pfadparameter der Quellen wurde nun mithilfe eines Folge-Befehls erstellt:

$PfadParameterQuelle=Folge(Wenn(n\leq 1,n),n,0,t,{\frac {1}{SpruehHaeufigkeit-1}})$

Um die Quellen auf dem vorgegebenen Fahrweg anzuzeigen, folgt:

$Quellen=Zip(Punkt(Wingert,PP),PP,PfadParameterQuelle)$

Da die Ausbreitung mithilfe der Kreisfunktion in GeoGebra dargestellt werden soll, benötigen wir für den Radius des Kreises eine dynamische Funktion. Hierfür haben wir zuerst einen weiteren Schieberegler Radius angelegt, der für die maximale Ausbreitung steht. Damit sich die Ausbreitungskreise außerdem jeweils dynamisch entwickeln, wurde nun noch eine Liste mit SprühHäufigkeit-swerten erstellt, deren Werte sich von 0 bis 1 entwickeln:

$tDynPerKreis=Folge(Wenn(n\leq 1,Min(tDyn,t-n)\cdot {\frac {1}{tDyn}},n,0,t,{\frac {1}{SpruehHaeufigkeit-1}})$

Damit kann nun eine dynamische Liste der Ausbreitungskreise erstellt werden:

$SpruehWolke=Zip(Kreis(Punkt(Wingert,PP),r\cdot Radius),PP,PfadParameterQuelle,r,tDynPerKreis)$(siehe Abb 1.1)

Abb. 1.1

Abb. 1.2

Zur Betrachtung einzelner Kreise wurde weiter eine Anzeigefunktion entwickelt, mit der sich ein Kreis in einer anderen Farbe darstellen lässt.

Mit tDyn besitzt das vorliegende Modell außerdem bereits eine Einstellungsmöglichkeit für die Ausbreitungs- (Konvektions-)geschwindigkeit. (vlg. Abb. 1.1 mit Abb. 1.2)

Zur Berechnung der Sprühkonzentration innerhalb der Kreise, wird von einer Ausgangskonzentration SprühKonz mg ausgegangen.

Abb. 1.3

SprühKonz wird wieder mit einem Schieberegler dargestellt, sodass man mit verschieden Ausgangskonzentrationen experimentieren kann. Für die Berechnung der SprühKonzPerPunkt folgt nun mit der Flächenformel für Kreise.

$SpruehKonzPerPunkt={\frac {SpruehKonz}{1+\pi \cdot (r\cdot R)^{2}}}$

In GeoGebra erstellen wir hierfür zwei weitere Listen:

$WolkenFlaechen=Zip(Flaeche(k),k,SpruehWolke)$

Und

$SpruehKonzPerPunkt=Zip({\frac {SpruehKonz}{1+Flaeche}},Flaeche,WolkenFlaechen)$

Diese Konzentration wird nun außerdem, für den jeweiligen Kreis, zusammen mit der Anzeigefunktion ausgegeben. (siehe Abb. 1.3)

Es fehlt nun nur noch die Berechnung der Konzentration an einem beliebigen Punkt, zu einer gewissen Zeit, wobei die Zeit per Schieberegler eingestellt wird. Die Schwierigkeit liegt in den vielfachen Überschneidungen der Kreise, die mit der Zeit zunehmen.

Zur Lösung berechnen wir den Abstand eines beliebigen Punktes vom jeweiligen Mittelpunkt eines Kreises. Über den Satz des Pythagoras bekommen wir die allgemeine Formel:

$d={\sqrt {(}}x1+x2)^{2}+(y1+y2)^{2}$

In GeoGebra können wir einfach den Befehl: $Abstand((x1,y1),(x2,y2))$ anwenden.

Verknüpft mit einem Wenn Befehl können wir uns nun die Konzentrationen derjenigen Kreise angeben lassen, in denen sich unser Messpunkt A befindet.

$SpruehKonzUmPunkt=EntferneUndefiniert(Zip(Wenn(Abstand(A,PP\leq r\cdot R),c),PP,Quellen,r,tDynPerKreis,c,SpruehKonzPerPunkt))$

Addiert man nun die Elemente der entstandenen Liste bekommt man die Konzentration im Punkt A:

$SpruehKonzImPunkt=Summe(SpruehKonzUmPunkt)$

Diese Konzentration wird nun auch auf der GeoGebra-Oberfläche angezeigt. Für den Punkt A wird außerdem ein Eingabefeld erstellt, sodass die Messpunkte leicht und unkompliziert geändert werden können. (Siehe Abb. 1.4)

Abb. 1.4

Probleme des 1. Modellierungszyklus

1. Die Schadstoffe breiten sich nicht linear aus, es ist viel mehr anzunehmen, dass die Konzentration am Ausgangsort stets am höchsten ist und mit zunehmender Distanz stetig abnimmt.

2. Wind und Fahrtrichtung als bestimmende Konvektionsgrößen sind außen vorgelassen.

3. Die Annahme von stationären Quellen, waren/sind eine für uns notwendige Vereinfachung gewesen, entsprechen aber nicht der Sprühbewegung einer fahrenden Quelle

4. Das Modell ist beschränkt in seiner Konstruktion, wie z.B. in der Tatsache, dass es von einer maximalen Ausbreitung ausgeht und damit die Endsituation gewissermaßen vorwegnimmt.

Modellierungszyklus 2

Zielsetzung

Ziel des zweiten Modellierungszyklus ist es das in Zyklus 1 erstellte Modell, von einer rein anschaulichen Ebene, auf eine mathematisch fundiertere Basis zu stellen. Wobei wir einerseits eine genaue Berechnung der Schadstoffkonzentration zu einem bestimmten Zeitpunkt an einem Punkt erreichen wollen und andererseits ein anschauliches Modell der Schadstoffverteilung im 2D-Raum.

Annahme

Die Ausbreitung wird durch die zweidimensionale Fundamentallösung beschrieben, welche, um im Rahmen der Sekundarstufe 2 zu bleiben, als gegeben angenommen wird.

$H({\vec {x}},v)={\frac {1}{(4pi\cdot v)}}\cdot e^{\frac {-\lVert {\vec {x}}-{\vec {u}}\rVert ^{2}}{4v}}$

v= Zeit seit Austritt

u=Austrittsort

Ausbreitungsgeschwindigkeit= $10^{-3}{\frac {m}{s}}$

Durchlauf 1

Zur dynamischen Berechnung der Schadstoffkonzentration zu einem Zeitpunkt, bleiben wir in der Anschaulichkeit des 1 Modells und modifizieren es u.a. mit der Fundamentallösung so, dass es den realen Begebenheiten besser entsprechen sollte.

Hierfür brauchen wir erst einmal Ausbreitungswolken, die nicht von einem vordefinierten Radius abhängen, sondern nur von der Zeit. D.h. wir brauchen eine elegantere Lösung für den dynamischen Anteil.

Wir erstellen einen weiteren Schieberegler $T$ für die vergangene Zeit in Sekunden und synchronisieren ihn mit $t$, den wir weiter als Pfadparameter benötigen. Die Zeit in $t$ wird durch ${\frac {T}{1000}}s$ beschrieben.

Unsere vorgegebene Strecke hat eine Länge von $255m$ und ist nach $1000s$ abgefahren, damit beträgt die Bewegungsgeschwindigkeit unserer Sprühquelle

${\frac {255}{1000}}{\frac {m}{s}}=0.92{\frac {km}{h}}$.

Wir erstellen nun eine weitere Liste für die Zeitpunkte der Schadstoffaustritte:

$tmoment=Zip(1000\cdot w,w,Pfadparameterquelle)$

Damit folgt für $v$ die Liste:

$v=Zip(10^{-3}\cdot (T-tmoment),tmoment,tmoment)$

Da die Fundamentallösung in ihrer Art einer Gaußschen Glockenkurve entspricht, nehmen wir für den Radius die 3-Fache Standardabweichung der Fundamentallösung, in der $99.73\%$ der Werte liegen. Für die Standardabweichung gilt

$\sigma ^{2}=2\cdot v\Rightarrow \sigma ={\sqrt {2\cdot v}}$

Damit gilt für unseren Radius: $3\cdot {\sqrt {2\cdot v}}$

Für die Listenberechnung der Konzentrationen um einen Punk folgt damit:

$SpruehKonzUmPunkt=EnteferneUndefiniert(Zip(Wenn(Abstand(A,PP)\leq 3\cdot {\sqrt {2v}},{\frac {1}{4\cdot \pi \cdot v}}\cdot e^{\frac {-Abstand(A,PP)^{2}}{4\cdot v}}),PP,Quellen,v,v))$

Für die Konzentration im Punkt gilt dann wieder:

$SpuehKonzImPunk=Summe(SpruehKonzUmPunkt)$

Abb. 2.1

Nach Durchlauf 1 beschreibt die Mathematik des Modells die Realität zwar besser, nur passen nun Mathematik und Anschauung des Modells nicht mehr so recht zusammen. Die passende Anschauung wird in Durchlauf 2 im 3D-Raum erstellt.

Durchlauf 2

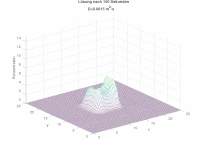
Nun erstellen wir ein 3D-Modell der Konzentrationsverteilung. Da die Berechnung für GeoGebra ein ganz schön harter Knochen ist, werden alle anderen Berechnungen, die nicht direkt zur Darstellung der Verteilung notwendig sind, gelöscht.

Für die Berechnung der einzelnen Konzentrationsfunktionen folgt nun mit der euklidischen Norm im 2D-Raum:

$Konzentrationsfunktion=Zip(SpuehKonz\cdot {\frac {1}{4\cdot \pi \cdot v}}\cdot e^{\frac {-{\sqrt {(x-x(PP))^{2}+(y-y(PP))^{2}}}}{4\cdot v}},v,v,PP,Quellen)$ (siehe Abb. 2.2)

Und für die Gesamtverteilung:

$Gesamtkonzentration(x,y)=Summe(Konzentrationsfunktion)$ (siehe Abb. 2.3)

Abb. 2.2

Abb. 2.3

Nach Modellierungszyklus 2, haben wir bereits einige der Probleme des 1. Zykluses behoben. Wobei bestimmende Konvektionsgrößen weiter nicht berücksichtigt wurden

Da die Berechnung des 3D-Modells bereits sehr lange Zeit in Anspruch genommen hat, trotz ausreichend vorhandener Rechenleistung des Computers und damit die Grenzen von GeoGebra erreicht wurden, werden wir infolgedessen für den nächsten Modellierungszyklus auf Octave wechseln.

Modellierungszyklus 3

Zielsetzung

Im Anschluss an die Ergebnisse des Modellierungszyklus 2 soll wieder eine Schadstoffverteilung, mit einer sich bewegenden Quelle modelliert werden.

Es wird der Vorgang der Diffusion betrachtet. Die Berechnung der Konzentration soll über die Methode der finiten Differenzen erreicht werden.

Annahmen

-         Es wird nur die eigenständige Diffusion des Stoffes betrachtet, keine Konvektion

-         Die Berechnung der 2D-Diffusion erfolgt innerhalb von Matrizen über eine Approximation der homogenen Diffusionsgleichung

-         Konstanter Diffusionskoeffizient

Durchführung

Zur Lösung der Diffusion über die finite Differenz, wird für die Länge der Zeiteschritte $dt=1$ gewählt. Die Diffusionskonstante soll $D=1.5*10^{-3}{\frac {m}{s}}$ betragen.

Abb. 3.1 Starparameter

In Octave wird ein $x,y$-Koordinatenfeld der Länge xend=yend aufgespannt, wobei die Schrittweite nach $x$ bzw. $y$ über eine beliebig gewählte Zahl an Gitterpunkten definiert wird.

Da außerdem die Diffusion auch nach dem Ende der Konzentrationsaustragung betrachtet werden soll, werden für die Quelle Anfangsbedingungen festgelegt, die beschreiben wie lange und schnell sich die Quelle bewegt.

Abb. 3.2 Quellfunktion

Für die bewegte Konzentrationsquelle wird eine Quellfunktion erstellt, die im definierten x,y-Feld, auf den dazugehörigen Gitterpunkten, über die zweidimensionale euklidische Norm, diejenigen Gitterpunkte aussucht, auf denen neue Konzentrationspunkte verteilt werden soll.

Um eine gleichmäßigere Verteilung zu erreichen wird außerdem, die für jeden Schritt neu erstellte Quellmatrix so bereinigt, dass an Gitterpunkten nur je einmal eine Konzentration ausgelegt wird.

Abb. 3.3 Konzentrationsberechnung

Die Berechnung der Konzentrationsdiffusion erfolgt nun über die approximierte Diffusionsgleichung, die auf eine Matrizenrechnung angewandt werden kann.

${\frac {\partial u(x,y,t)}{\partial t}}=D\cdot \Delta u(x,y,t)\Longrightarrow u(x,y,t+\Delta t)=D\cdot \left({\frac {u(x-\Delta x,y,t)-2\cdot u(x,y,t)+u(x+\Delta x,y,t)}{\Delta x^{2}}}+{\frac {u(x,y-\Delta y,t)-2\cdot u(x,y,t)+u(x,y+\Delta y,t)}{\Delta y^{2}}}\right)$

Zu guter Letzt wird noch für jede Sekunde die Konzentrationsmatrix gespeichert, sodass am Ende für beliebige Zeitschritte geplottet werden kann.

• 
• 
• 
• 

Reflektion

Gegenüber Modellierungszyklus 2 in GeoGebra wurde über die Berechnung in Matrizen mit Octave, ein Modell implementiert, dass in der Lage ist in überschaubarer Zeit, die gewünschten Berechnungen durchzuführen. Außerdem ist die Quellfunktion nun nicht mehr von fest definierten Punkten limitiert, sondern mit seiner durchlaufenden Funktionsvorschrift einer realen Bewegung bereits näher.

Über die Implementierung mit for- und if-Schleifen ist das Programm außerdem übersichtlich und nachvollziehbar. Die Kehrseite ist allerdings, dass die Berechnung von for- und if-Schleifen immer noch sehr Arbeits- und Zeitintensiv ist, wenn auch schon viel weniger als das vorhergehende Programm in GeoGebra. Die Alternative wäre eine Berechnung über Funktionen und nicht über Matrizen.

Weiter ist das Modell noch sehr weit davon entfernt den Ansprüchen einer realen Begebenheit zu genügen. Weitere Aspekte die es zu beachten gelte, wenn man an dem Modell weiter arbeiten würde, wären Konvektionsfelder(Wind, Regen, Wärme), Grenzen innerhalb des Diffusionsfeldes(Wingertzeilen, Berge und Täler) und zu guter Letzt müsste man das Modell in die 4-Dimensionalität bringen.