4.3 Implizite Runge-Kutta Verfahren

Wenn die Koeffizientenmatrix ${\textstyle A}$ im Butcher Tableau eines Runge-Kutta Verfahrens eine vollbesetzte Matrix ist, hängt die Berechnung der Funktionsauswertungen ${\textstyle k_{j}}$ für jedes ${\textstyle j=1,\ldots ,s}$ von anderen ${\textstyle k_{1},\dots k_{s}}$ ab, insbesondere auch von den ${\textstyle k_{j},k_{j+1},\dots k_{s}}$ , siehe (4.1). Das einfachste iRKV ist das schon bekannte implizite Eulerverfahren, weitere Beispiele sind die implizite Mittelpunkt- und Trapezregel:

Implizite Mittelpunktregel, ${\textstyle s=1}$ :

${\begin{aligned}k_{1}&=&f{\big (}t_{i}+{\frac {h}{2}},\eta _{i}+{\frac {h}{2}}k_{1}{\big )}\\\eta _{i+1}&=&\eta _{i}+hk_{1}\qquad \qquad \quad \end{aligned}}$

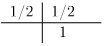
Implizite Trapeztregel, ${\textstyle s=2}$ :

${\begin{aligned}k_{1}&=&f(t_{i},\eta _{i})\qquad \quad \quad \quad \quad \quad \quad \\k_{2}&=&f{\big (}t_{i}+h,\underbrace {\eta _{i}+{\frac {h}{2}}(k_{1}+k_{2})} _{\eta _{i+1}}{\big )}\qquad \\\eta _{i+1}&=&\eta _{i}+{\frac {h}{2}}(k_{1}+k_{2})\qquad \quad \qquad \qquad \\&\equiv &\eta _{i}+{\frac {h}{2}}{\Big (}f(t_{i},\eta _{i})+f(t_{i+1},\eta _{i+1}){\Big )}.\end{aligned}}$

Eine wichtige Untermenge der iRKV sind sogenannte Gauß-Verfahren, diese ermöglichen die größtmögliche Ordnung im Hinblick auf die Stufenzahl. Diese Verfahren gehören zu den sogenannten Kollokationsverfahren und werden von der Gauß-Quadratur abgeleitet, dieser Tatsache verdanken sie ihrem Namen. Die Gauß-Verfahren, wie auch andere (aber nicht alle) iRKV haben gute Stabilitätseigenschaften, die insbesondere für ’steife’ Probleme von großer Bedeutung sind.

Steife Probleme

Der Bergriff eines steifen Problems entstand bei der Anwendung der numerischen Methoden zur Lösung einer Differentialgleichung, wenn diese sehr kleine bzw. im Laufe des Verfahrensfortschritts immer kleinere Schrittweiten benötigt, um eine brauchbare, konvergente Lösung zu produzieren. Explizite Verfahren wie Eulerverfaren oder auch die eRKV höherer Ordnung mit fester Schrittweite versagen in solchen Fällen; Verfahren mit Schrittweitensteuerung generieren immer kleinere Schrittweiten bis zur Null (im Rahmen der Rechnergenauigkeit), demzufolge bewegen sie sich irgendwann nicht mehr von der Stelle, sie bleiben stehen - daher kommt der Begriff ’steif’.

Zu den steifen Problemen gehören Differentialgleichungen mit Lösungen mit hohen Veränderungsraten, oder Systeme mit sehr unterschiedlich schnell wachsenden Lösungskomponenten. Hierbei generiert ein explizites Verfahren die Lösungsapproximation im nächsten Zeitschritt anhand der vorherigen, in stark dynamischen Systemen nicht mehr aktueller, fehlerbehafteter Steigungen/Informationen und somit schießt das explizite Verfahren schnell über das Ziel hinaus.

Beispiele für steife Probleme sind lineare Differentialgleichungssysteme, deren Matrix sehr unterschiedliche Eigenwerte besitzt, oder etwa Differentialgleichungen, die chemische Reaktionen mit unterschiedlich schnell reagierenden Stoffen beschrieben. Durch die gute Stabilitätseigenschaften der impliziten Einschrittverfahren, die im aktuellem Schritt deren Verlauf an die zukunftige (noch stärkere) Steigung anpassen und somit auch für größere Schrittweiten ${\textstyle h}$ gute Ergebnisse liefern, sind iRKV besonders für steiffe Probleme geeignet.

Abbildung 4.1: Lösungskomponenten eines steiffen Differentialgleichungssystems, exakte Lösung ${\textstyle y_{1}(t)=e^{10t},\ y_{2}=1000e^{-10t}}$ und Approximation mit explizitem Eulerverfahren, ${\textstyle h=0.125}$ .

Bei impliziten Runge-Kutta Verfahren werden die Stufen ${\textstyle k_{j}}$ durch die Lösung des Gleichungssystems (4.1) berechnet. Die Existenz der Lösung dieses ggf. nichtlinearen Gleichungssystems ist nicht immer garantiert oder durch iterative Methoden erreichbar. Eine hinreichende Bedingung für die Existenz einer solchen Lösung und der Konvergenz der iterativen Fixpunktmethode ist eine hineichend kleine Schrittweite ${\textstyle h}$ :

Satz 4.2 (Butcher 1964)

Sei ${\textstyle f}$ stetig auf ${\textstyle {\mathbb {R} }\times {\mathbb {R} }^{m}}$ und Lipschitz stetig bezüglich ${\textstyle y}$ mit Lipschitz-Konstante ${\textstyle L}$ . Gelte für die Schrittweite ${\textstyle h}$ $h<{\frac {1}{L\||A\||_{\infty }}}={\frac {1}{L\mathrm {max} _{i}\sum _{j=1,\ldots s}|a_{ij}|}}.\qquad (4.12)$

Dann besitzt das Gleichungssystem (4.1), $k_{j}=f{\Big (}t_{i}+hc_{j},\eta _{i}+h\sum _{\nu =1}^{s}a_{jm}k_{\nu }{\Big )}\quad \ \ j=1,\ldots ,s$

eine eindeutige Lösung, die durch sukzessive Substitution (Fixpunktiteration) berechnet werden kann. Ist zudem ${\textstyle f\in C^{p}({\mathbb {R} }\times {\mathbb {R} }^{m})}$ , dann sind die ${\textstyle k_{j}}$ als Funktionen von ${\textstyle h}$ auch ${\textstyle p}$ -mal stetig differenzierbar.

Beweis. Sei einfachheitshalber ${\textstyle m=1}$ an. Die Lösung des (nichtlinearen) Gleichungssystem (4.1) für ${\textstyle k_{1},\ldots k_{s}}$ lässt sich iterativ bestimmen: $k_{j}^{(m+1)}=f{\Big (}t_{i}+hc_{j},\eta _{i}+h\sum _{\nu =1}^{s}a_{j\nu }k_{\nu }^{(m)}{\Big )}\quad \ \ j=1,\ldots ,s.\qquad (4.13)$

Schreibt man das Gleichungssystem (4.1) in die vektorielle Form um, ${\vec {K}}=F({\vec {K}}),$

mit ${\textstyle {\vec {K}}=(k_{1},\ldots k_{s})^{T}\in {\mathbb {R} }^{s},\ F:{\mathbb {R} }^{s}\to {\mathbb {R} }^{s},}$ ${\begin{aligned}F_{j}({\vec {K}}):=f{\Big (}t_{i}+hc_{j},\eta _{i}+h\sum _{\nu =1}^{s}a_{j\nu }k_{\nu }{\Big )}=f{\Big (}t_{i}+hc_{j},\eta _{i}+hA_{j}\cdot {\vec {K}}{\Big )}\quad \ j=1,\ldots ,s\end{aligned}}$

so erhält man Anstelle von (4.13) die Iterationsvorschrift ${\vec {K}}^{(m+1)}=F{\big (}{\vec {K}}^{(m)}{\big )}\qquad (4.14)$

mit einem Startvektor ${\textstyle K^{(0)}.}$

Nach dem Fixpunktsatz von Banach, siehe Satz 2.1, Kapitel 2, existiert eine eindeutige Lösung, ein Fixpunkt von ${\textstyle {\vec {K}}=F({\vec {K}})}$ , wenn ${\textstyle F}$ eine Selbstabbildung und kontrahierend ist. Für eine Funktion ${\textstyle F:{\mathbb {R} }^{s}\to {\mathbb {R} }^{s}}$ ist ${\textstyle F({\mathbb {R} }^{s})\subseteq {\mathbb {R} }^{s}}$ , also immer eine Selbtsabbildung.
Nun untersuchen wir, ob ${\textstyle F}$ kontrahierend ist. Wir schätzen mihilfe der Lipschitz-Stetigkeit der Funktion ${\textstyle f}$ und der Dreiecksungleichung für den Betrag inMaximumnorm: ${\begin{aligned}\|F({\vec {K}})^{1}-F({\vec {K}}^{2})\|_{\infty }=\max _{j=1,...,s}{\Big |}f{\Big (}t_{i}+hc_{j},\eta _{i}+h\sum _{\nu =1}^{s}a_{j\nu }k_{\nu }^{1}{\Big )}-f{\Big (}t_{i}+hc_{j},\eta _{i}+h\sum _{\nu =1}^{s}a_{j\nu }k_{\nu }^{2}{\Big )}{\Big |}\\{\stackrel {L-stetig}{\leq }}\max _{j}hL{\Big |}\sum _{\nu =1}^{s}a_{j\nu }(k_{\nu }^{1}-k_{\nu }^{2}){\Big |}\leq hL\max _{j}\sum _{\nu =1}^{s}|a_{j\nu }|\max _{\nu }|k_{\nu }^{1}-k_{\nu }^{2}|\\=hL\||A\||_{\infty }\|K^{1}-K^{2}\|_{\infty }.\end{aligned}}$

Aus dieser Abschätzung folgt dass ${\textstyle F}$ kontrahierend ist in Banach Raum ${\textstyle {\mathbb {R} }^{s},\|\cdot \|_{\infty }}$ , falls ${\textstyle hL\||A\||_{\infty }\|<1}$ . Demzufolge hat die Abbildung ${\textstyle F}$ für ${\textstyle h<1/(L\||A\||_{\infty })}$ in ${\textstyle {\mathbb {R} }^{s}}$ einen eindeutigen Fixpunkt, ${\vec {K}}^{\star }=F({\vec {K}}^{\star }),$

und die Iteration (4.13), (4.14) konvergiert gegen diesen Fixpunkt. Die Aussage über die p-fache stetige Differenzierbarkeit von ${\textstyle k_{j}}$ belassen wir ohne Beweis. ◻

Bemerkung zur Lösbarkeit der iRKV

Die Einschränkung der Schrittweite ${\textstyle h}$ kann bei großen ${\textstyle L}$ -Konstanen (d.h. bei ${\textstyle f}$ mit hohen Werten der Ableitung ${\textstyle {\frac {\partial f}{\partial y}}\approx L}$ ) sehr restriktiv sein und zur langsamen Konvergenz des Fixpunktverfahrens führen. Der Ausweg in diesen Fällen ist die Anwendung eines anderen iterativen Verfahren mit höherer Konvergenzgeschwindigkeit zur Berechnung nun von ${\textstyle k_{j}}$ , wie Newton-, Sekanten-, oder Quasi-Newton Verfahren. Diese Verfahren konvergieren auch für größere ${\textstyle h}$ , da sie superlineare Konvergenzgeschwindigkeit haben, wenn der Startwert günstig, innerhalb des sog. Konvergenzintervalls gewählt ist.
Ist die Funktion ${\textstyle f}$ lediglich nur lokal Lipschitz stetig in ${\textstyle y}$ , d.h. nur in einer Umgebung von ${\textstyle K^{(0)}}$ , dann resultieren weitere Beschränkungen auf die Schrittweite ${\textstyle h}$ , um die Selbstabbildungs-Eigenschaft zu garantieren.
Die Lipschitz-Stetigkeit der Verfahrensfunktion ${\textstyle \Phi }$ eines eRKV, wie auch eines iRKV bezüglich ${\textstyle y}$ folgt aus der Lipschitz-Stetigkeit von ${\textstyle f}$ . Damit sind auch die iRKV mit Konsistenzordnung p konvergent mit der Konvergenzordnung p. (siehe Satz 3.1)