Formale Aspekte

Namen der Verfasser der Lernumgebungsdokumentation

Sarina Renoth und Sarah Stummer

E-Mail-Adressen und Datum

s8sareno@stud.uni-saarland.de

s8sastum@stud.uni-saarland.de

Datum: 01.09.2021

Inhaltsaspekte

Name der Lernumgebung

kidsProof: Malkreuz x Distributivgesetz

Kurzbeschreibung der Lernumgebung

Das mathematische Beweisen findet im schulischen Kontext in der Regel in höheren Klassenstufen auf formaler Ebene statt, wobei der ausschließlich formale Zugang häufig mit mangelnder Nachvollziehbarkeit der mathematischen Handlungen verbunden ist. Als Vorstufe des formalen Beweisens in den weiterführenden Schulen beschäftigt sich diese Lernumgebung mit dem präformalen Beweisen, welches bereits in der Primarstufe umgesetzt werden kann. Dabei können die Schülerinnen und Schüler erste positive Erfahrungen und Erfolgserlebnisse mit dem mathematischen Beweisen sammeln und diese Erfahrungen in höheren Klassenstufen im Sinne des Spiralcurriculums entsprechend nutzen und erweitern.

Üblicherweise wird das Malkreuz in der Primarstufe als halbschriftliche Rechenstrategie eingeführt, ohne dass deren Gültigkeit hinterfragt bzw. der mathematische Hintergrund hergeleitet wird. In dieser Lernumgebung können die Schülerinnen und Schüler den mathematischen Hintergrund des Malkreuzes und damit das Distributivgesetz als allgemeingültiges Gesetz nachvollziehen, wobei gleichermaßen auch das Hinterfragen mathematischer Aussagen angeregt und das Verständnis für mathematische Inhalte und Zusammenhänge gefördert wird. In der Lernumgebung kommen sowohl analoge als auch digitale Arbeitsmaterialien zum Einsatz. Während sich die Schülerinnen und Schüler ausgehend von einem vorgefertigten Malkreuz den mathematischen Hintergrund des Malkreuzes am analogen 400er Punktefeld unter Hinzunahme weiterer Materialien (Malwinkel, Buntstifte, Holzspieße als „Kreuz“) erarbeiten, findet mithilfe der Website „Partial Product Finder“ eine Generalisierung statt, wobei die Gültigkeit des Distributivgesetzes erkannt wird. Die Aktivitäten am digitalen Material werden von den Schülerinnen und Schülern wiederum in vorgefertigte analoge Malkreuz-Vorlagen übertragen. Für das Anfertigen von Notizen oder Skizzen stehen weiße Blätter ohne Lineatur bzw. Karomuster zur Verfügung.

Ungefährer Zeitbedarf zur Durchführung

Die Durchführung der Lernumgebung umfasst ca. 30 Minuten.

Adressaten der Lernumgebung

Die Lernumgebung ist für die Klassenstufe drei konzipiert. Angesichts dessen, dass innerhalb der Lernumgebung im Zahlenraum bis 2500 beliebig variiert werden kann, ist durchaus auch ein Einsatz in anderen Klassenstufen der Primarstufe möglich, sofern die untenstehenden fachlichen Voraussetzungen erfüllt sind (s. Kapitel 3.1 "Mathematische Analyse").

Zentrale Aufgabenstellungen und Arbeitsaufträge in der Lernumgebung

Gestaltung des Einstiegs:

Die thematische Einbettung der Lernumgebung ergibt sich aus der Lebenswelt der Schülerinnen und Schüler. So zeigen die für die Durchführung der Lernumgebung ausgewählten Schülerinnen und Schüler sehr großes Interesse für das Themenfeld „Studium“ und werden durch die thematische Einbettung der Lernumgebung aktiv in ihr Interessensfeld miteinbezogen.

LP: „Ich war gestern wieder an der Uni und hatte eine Mathe-Vorlesung. Mein Professor hat in der Vorlesung an der Tafel ganz schnell große Malaufgaben mithilfe des Malkreuzes gelöst. Viele Studierende haben nicht ganz verstanden, warum in dem Malkreuz unten rechts in dem Feld das richtige Ergebnis herauskommt. Ich habe dir eine Aufgabe aus der Vorlesung mal mitgebracht.“

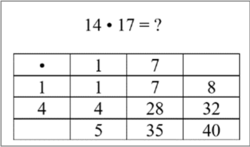
Die Lehrperson legt ein Bild des vorgefertigten Malkreuzes mit der Aufgabe 14 • 17 vor (s. Kapitel 4.4 "Potenzial des Einsatzes (digitaler) Medien"). Dabei werden bewusst zweistellige Faktoren gewählt, da das Kleine Einmaleins in der Regel automatisiert beherrscht und so der Vorteil der Nutzung des Malkreuzes für die Lernenden ersichtlich wird.

LP: „Warum kommt unten rechts das richtige Ergebnis heraus?“

Aufgabenstellungen und Arbeitsaufträge in der Lernumgebung:

Warum kommt unten rechts das richtige Ergebnis heraus?

Das Malkreuz ist den Schülerinnen und Schülern als halbschriftliche Rechenstrategie der Multiplikation bekannt. Durch diese Fragestellung werden die Lernenden dazu angeregt, diese nicht lediglich als solche hinzunehmen, sondern deren mathematische Gültigkeit zu hinterfragen (vgl. Brunner, 2014, S. 87 - 88). Im Malkreuz wird die Ausgangsmalaufgabe in vier Teilmalaufgaben zerlegt und die Teilprodukte addiert. Diese Vorgehensweise kann am 400er Punktefeld sehr gut visuell veranschaulicht werden. Den Schülerinnen und Schülern wird ein 400er Punktefeld, ein Malwinkel, Buntstifte, Holzspieße und weiße Blätter zur Verfügung gestellt. Die Schülerinnen und Schüler stellen die Ausgangsmalaufgabe 14 • 17 mithilfe des Malwinkels am 400er Punktefeld dar. Zur Darstellung der Teilmalaufgaben im 400er Punktefeld bestehen verschiedene Möglichkeiten wie beispielsweise das Einkreisen der Malaufgaben mithilfe der Buntstifte, das Einzeichnen eines Kreuzes oder die Nutzung der Holzspieße, die zu einem Kreuz gelegt werden.

Mögliche Impulse:

„Stelle die Aufgabe 14 • 17 am 400er Punktefeld dar. Der Malwinkel hilft dir dabei. Erkläre, was du tust.“

„Wie kannst du die Teilmalaufgaben aus dem Malkreuz im 400er Punktefeld darstellen? Nutze zum Beispiel die Stifte oder die Holzspieße. Erkläre, was du tust.“

Wie kann man die Aufgabe 14 • 17 noch teilen? Kommt dann auch das gleiche Ergebnis heraus?

Die Faktoren einer Multiplikationsaufgabe können jeweils in beliebige und beliebig viele Summanden zerlegt und die Teilprodukte miteinander addiert werden, ohne dass sich das Ergebnis der Ausgangsmultiplikationsaufgabe ändert. Die Schülerinnen und Schüler arbeiten hierzu mit der Website „Partial Product Finder“. Die Malaufgabe 14 • 17 ist bereits eingestellt.

Mögliche Impulse:

„Verschiebe die Regler.“

„Was passiert, wenn du die Regler verschiebst?“

„Was passiert mit der Anzahl der Kästchen, wenn du die Regler verschiebst?“

Funktioniert das Prinzip auch bei anderen Malaufgaben? Übertrage die Malaufgaben und die Teilmalaufgaben von der Website in ein Malkreuz.

Das Distributivgesetz ist allgemein gültig und nicht auf Einzelfälle beschränkt. Damit die Lernenden dafür sensibilisiert werden, dass nicht anhand von Einzelfällen allgemeingültige Schlussfolgerungen abgeleitet werden können, überprüfen die Schülerinnen und Schüler die Gültigkeit des Distributivgesetzes anhand mehrerer Aufgabenbeispiele mithilfe des „Partial Product Finder“ (vgl. Meyer & Prediger, 2009, S. 6). Dazu können die Schülerinnen und Schüler beliebige Malaufgaben selbst einstellen und beliebige Teilungen anhand der Regler vornehmen.

Mögliche Impulse:

„Probiere verschiedene Malaufgaben aus. Gebe sie oben links in die Felder ein.“

„Verschiebe die Regler.“

„Was passiert, wenn du die Regler verschiebst?“

„Was passiert mit der Anzahl der Kästchen, wenn du die Regler verschiebst?“

Die Schülerinnen und Schüler übertragen die auf der Website am Rechteckgitter dargestellten Ausgangs- und Teilmalaufgaben von der ikonischen auf die formale Ebene wobei ein intermodaler Transfer stattfindet und somit mathematische Erkenntnisprozesse der Schülerinnen und Schüler unterstützt werden (vgl. Käpnick & Benölken, 2020, S. 66).

Technische Voraussetzungen

Pro Schüler bzw. Schülerin wird ein Tablet mit Touchfunktion bzw. ein Laptop oder Computer mit Maus benötigt. Alle Geräte sollten aufgeladen sein und über einen Internetzugang verfügen. Die Website „Partial Product Finder“ sollte vor der Aushändigung der Geräte an die Lerngruppe bereits aufgerufen sein. Hierbei ist auf die Verwendung eines kindersicheren Browsers zu achten.

Mathematischer Gehalt der Lernumgebung

Mathematische Analyse

Mathematischer Inhalt der Lernumgebung ist der präformale Beweis des Distributivgesetzes. Ausgangspunkt ist das Malkreuz, welches den Schülerinnen und Schülern als halbschriftliche Rechenstrategie der Multiplikation bekannt ist und auf dem Distributivgesetz basiert. Ausgehend von einem vorgefertigten Malkreuz zur Malaufgabe 14 • 17 übertragen die Lernenden die im Malkreuz dargestellte Aufgabe und dargestellten Teilprodukte auf ein analoges 400er Punktefeld, wodurch der Wechsel von der formalen auf die ikonische Ebene erfolgt. Im Anschluss probieren die Schülerinnen und Schüler weitere Teilungen der Aufgabe 14 • 17 sowie weitere Ausgangsmalaufgaben mit entsprechenden Teilprodukten mithilfe des Rechteckgitters auf der Website „Partial Product Finder“ aus und überprüfen so die Gültigkeit des Distributivgesetzes. Anhand des Punktefeldes bzw. des Rechteckgitters erkennen die Lernenden, dass die Gesamtanzahl der Punkte bzw. Rechtecke, welche das Ergebnis einer Malaufgabe darstellen, unabhängig von den gebildeten Teilprodukten der Ausgangsmalaufgabe ist und dass dieser Zusammenhang für beliebige Malaufgaben gültig ist.

Zur Durchführung der Lernumgebung werden folgende mathematische Voraussetzungen verlangt:

Funktionsweise des Malkreuzes
Punktefeld und Malwinkel als mathematische Arbeitsmittel
Darstellung von Multiplikationsaufgaben am Punktefeld
sicheres Beherrschen des Kleinen und ggf. Großen Einmaleins (je nach Zahlenraum und Klassenstufe)
Addition zweier (oder mehrerer) Summanden (je nach Anzahl der Teilmultiplikationsaufgaben)
Zahlzerlegung in zwei oder mehrere Summanden
ausgebildetes Stellenwertverständnis des dezimalen Zahlsystems

Mathematikdidaktischer Gehalt der Lernumgebung

Didaktische Analyse

In der Lernumgebung können folgende, generelle Schwierigkeiten beim mathematischen Beweisen seitens der Schülerinnen und Schüler auftreten:

Angesichts dessen, dass das Malkreuz im schulischen Kontext üblicherweise als halbschriftliche Rechenstrategie eingeführt wird, kann ggf. ein mangelndes Beweisbedürfnis resultieren. So könnten die Lernenden beispielsweise argumentieren, dass ihnen das Malkreuz bereits bekannt ist und dahingehend kein Grund bestehe, sich intensiver mit dem Malkreuz zu beschäftigen (vgl. Brunner, 2014, S. 85). Weiterhin kann die Schwierigkeit auftreten, dass von Einzelfällen auf allgemeingültige Zusammenhänge geschlossen wird. So kann es vorkommen, dass die Lernenden nur wenige Ausgangsmalaufgaben und Teilprodukte bilden und ausgehend von diesen Einzelfeststellungen auf die Allgemeingültigkeit des Distributivgesetzes schließen. In diesem Zusammenhang kann zudem die Formulierung der gemachten Beobachtungen bzw. erkannten Zusammenhänge zu Problemen führen (vgl. Brunner, 2014, S. 85).

In der Lernumgebung können folgende, auf den Beweis der Lernumgebung bezogene fachliche Hindernisse seitens der Schülerinnen und Schüler auftreten:

Es besteht die Möglichkeit des ziffernweisen Rechnens im Malkreuz, welches in der Regel auf ein mangelndes Stellenwertverständnis zurückgeführt werden kann (vgl. Selter, Prediger, Nührenbörger & Hußmann, 2014, S. 120). Wie dies aussehen kann, wird an folgendem Beispiel deutlich:

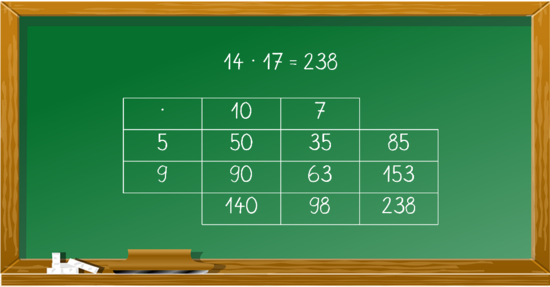
Weiterhin werden unter Umständen einzelne Teilprodukte nicht berücksichtigt, indem nur gleiche Stellenwerte miteinander multipliziert werden (vgl. Selter, Prediger, Nührenbörger & Hußmann, 2014, S. 120). Beispielsweise wird bei der Aufgabe 14 • 17 nur 10 • 10 und 4 • 7 gerechnet, wobei die Aufgaben 10 • 7 und 4 • 10 außer Acht bleiben. Eine weitere Schwierigkeit kann sich bei der Darstellung von Multiplikationsaufgaben im Punktefeld ergeben, wenn die Rolle der Faktoren im Punktefeld nicht klar ist (1 Faktor in der Spalte, 1 Faktor in der Zeile) (vgl. Technische Universität Dortmund, 2019, S. 1). Als mögliche Folge eines eingeschränkten Verständnisses für die flächige Darstellung der Multiplikation gilt das zählende Rechnen, wobei das Ergebnis der am Punktefeld dargestellten Malaufgabe durch Abzählen aller Punkte ermittelt wird.

„Gute“ Aufgaben & Differenzierung

Mathematische Ergiebigkeit (Kompetenzorientierung):

Die Lernumgebung bietet verschiedene Möglichkeiten der Förderung inhaltsbezogener und allgemeiner mathematischer Kompetenzen (vgl. KMK, 2004).

Folgende inhaltsbezogene Kompetenzen werden in der Lernumgebung angesprochen:

Muster und Strukturen: Die strukturierte Zahldarstellung am 400er Punktefeld durch die 5er und 10er Struktur muss erkannt und zur (quasi-)simultanen Zahlerfassung genutzt werden.

Zahlen und Operationen: Je nachdem, welche Zerlegungen der Ausgangsmalaufgaben vorgenommen werden und welche Teilmalaufgaben sich dadurch ergeben, soll das Kleine und ggf. Große Einmaleins automatisiert wiedergegeben werden können. Um die Zerlegung der Faktoren in zwei oder mehrere Summanden zu vollziehen, bedarf es der Zahlzerlegung. Zudem müssen die Grundrechenarten der Addition und Multiplikation beherrscht werden, wobei im Kopf gerechnet werden kann oder (halb)schriftliche Rechenstrategien eingesetzt werden können. Weiterhin muss das Malkreuz als halbschriftliche Rechenstrategie der Multiplikation bekannt sein. Mathematischer Inhalt der Lernumgebung ist das Distributivgesetz, welches in Form des Malkreuzes zum vorteilhaften Rechnen genutzt wird.

In der Lernumgebung wird eine Verbindung der Kompetenzbereiche „Muster und Strukturen“ und „Zahlen und Operationen“ hergestellt. So veranschaulicht die Visualisierung der Multiplikation am Punktefeld die Multiplikation als verkürzte Addition. Zudem fördert die Punktefelddarstellung der Multiplikation die multiplikative Grundvorstellung der räumlich-simultanen Anordnung.

Folgende allgemeine mathematische Kompetenzen werden in der Lernumgebung angesprochen:

Argumentieren: Mathematische Aussagen müssen hinterfragt und auf Korrektheit geprüft werden. Es müssen mathematische Zusammenhänge erkannt und Vermutungen entwickelt sowie Begründungen gesucht und nachvollzogen werden.

Darstellen: Multiplikationsaufgaben müssen am 400er Punktefeld dargestellt werden, beispielsweise unter Hinzunahme des Malwinkels. Es müssen geeignete Darstellungen der entsprechenden Teilmultiplikationsaufgaben am 400er Punktefeld gefunden werden, beispielsweise durch Einzeichnen oder Legen eines Kreuzes oder Einkreisen der einzelnen Teilmalaufgaben. Die ikonische Darstellung der Ausgangs- und Teilmalaufgaben am Punktefeld bzw. Rechteckgitter muss in die formale Darstellung im Malkreuz übertragen werden und umgekehrt.

Kommunizieren: Eigene Vorgehensweisen werden beschrieben, wobei mathematische Fachbegriffe und Zeichen sachgerecht verwendet werden.

Problemlösen: Mathematische Kenntnisse, Fertigkeiten und Fähigkeiten (z. B. sicheres Beherrschen des Kleinen/Großen Einmaleins) müssen bei der Bearbeitung problemhaltiger Aufgaben angewendet werden. Dabei müssen Lösungsstrategien entwickelt und genutzt sowie Zusammenhänge erkannt, genutzt und auf ähnliche Sachverhalte übertragen werden.

Offenheit und „optimale“ Passung:

Das 400er Punktefeld und der Malwinkel sind als Arbeitsmittel vorgegeben. Zur Darstellung der Teilmalaufgaben im 400er Punktefeld steht eine Materialauswahl zur Verfügung (Buntstifte, Holzspieße). Dadurch ergeben sich unterschiedliche Möglichkeiten der Darstellung der Teilmalaufgaben am 400er Punktefeld.

Am digitalen Material besteht die Möglichkeit gemäß individuellen Fähig- und Fertigkeiten frei im Zahlenraum bis 2500 zu arbeiten. Dabei können beliebige Ausgangsmalaufgaben und beliebige Zerlegungen der Faktoren vorgenommen werden. Die Ermittlung der Ergebnisse der Teilmultiplikationsaufgaben und Addition der Teilprodukte kann auf unterschiedlichen Wegen erfolgen. So können diese zum Beispiel durch Kopfrechnen ermittelt oder individuelle Lösungswege auf den zur Verfügung stehenden weißen Blättern notiert werden.

Authentizität, Aktivierung und Motivation:

In der Lernumgebung soll das Distributivgesetz als allgemeingültiges mathematisches Rechengesetz erkannt werden. Gerade dieses Erkennen von allgemeingültigen Zusammenhängen bzw. Mustern spiegelt die Natur bzw. Grundstruktur der Mathematik wider. So erhalten die Lernenden einen authentischen Einblick in die Welt der Mathematik (vgl. Wittmann, 2014, S. 227). Durch das Herstellen eines Lebensweltbezugs, das Anknüpfen an die Interessen der Zielgruppe und das Stellen einer „Warum“-Frage wird in der Einstiegsphase ein Beweisbedürfnis geweckt.

Differenzierung:

Im Sinne der natürlichen Differenzierung arbeiten alle Lernenden am gleichen Lerngegenstand, wobei die Aufgabenstellung ein Lernen und Arbeiten auf unterschiedlichen Anspruchsniveaus ermöglicht und somit unterschiedliche Lernvoraussetzungen berücksichtigt werden (vgl. Freudenthal, 1974, S. 166, zitiert nach Scherer & Moser Opitz, 2010, S. 57). So sind die Multiplikationsaufgaben und die Zerlegungen der einzelnen Faktoren am digitalen Material frei wählbar, wodurch u. a. im Zahlenraum variiert werden kann. Auf der Website „Partial Product Finder“ besteht zudem die Möglichkeit, die Lösungen der Teilmalaufgaben und die Lösung der Ausgangsmalaufgabe anzuzeigen. Dadurch stellen etwaige Schwierigkeiten beim reinen Rechenprozess kein Hindernis dar, sich dennoch mit diesem präformalen Beweis bzw. der Lernumgebung auseinanderzusetzen. Bei der Durchführung im Klassenkontext kann zudem ein Lernen mit- und voneinander stattfinden, wodurch anregende bzw. zielführende Impulse seitens der Lehrperson ggf. weniger erforderlich sind als dies in der Eins-zu-eins-Situation der Fall ist.

Artikulation, Kommunikation, Soziale Organisation

Die Lernumgebung findet in der Eins-zu-eins-Situation zwischen der Lehrperson und einem Schüler bzw. einer Schülerin statt. Dabei sitzen Lehrperson und der bzw. die Lernende gemeinsam an einem Tisch. Im Einstieg berichtet die Lehrperson, in dem konkreten Fall die Studentin, von einer fiktiven Situation aus ihrer Lebenswelt, wobei das schülerbezogene Interessensfeld „Studium“ angesprochen wird. Ausgehend von der im Einstieg gestellten „Warum“-Frage operiert der Schüler bzw. die Schülerin zunächst am analogen Material. Dabei ist das Material in Form des 400er Punktefeldes und des Malwinkels vorgegeben, wobei allerdings verschiedene Möglichkeiten der Darstellung der Teilmalaufgaben umgesetzt werden können. Während des Handelns des Schülers bzw. der Schülerin hält sich die Lehrperson zurück und fordert ggf., falls dies nicht eigenständig von dem Schüler bzw. der Schülerin erfolgt, eine Verbalisierung des mathematischen Handelns ein. Dadurch wird es der Lehrperson möglich, im Falle von Schwierigkeiten zielführende Impulse zu geben. Anstelle der Vorgabe von Lösungen sollen die Impulse eine kognitive Aktivierung der Schülerinnen und Schüler initiieren (vgl. Brunner, 2014, S. 91 - 92). Hierbei ist zu beachten, dass nicht frühzeitig bzw. nach kurzen Stillephasen seitens des Schülers bzw. der Schülerin von der Lehrperson interveniert wird, sondern Zeit zum Nachdenken gegeben wird. Das hier beschriebene Verhalten der Lehrperson bezieht sich auf die gesamte Lernumgebung bzw. die Interaktion mit dem Schüler bzw. der Schülerin. Im Anschluss an das analoge Material erhält der Schüler bzw. die Schülerin das digitale Material. Um eine Verallgemeinerung der am analogen Material erkannten Zusammenhänge anzuregen, handelt der Schüler bzw. die Schülerin unter entsprechenden Impulsen der Lehrperson am Rechteckgitter der Website „Partial Product Finder“, wobei beliebige Malaufgaben und Teilmalaufgaben durch den Schüler bzw. die Schülerin eingestellt werden können. Dabei gibt die Lehrperson ggf. Hinweise bezüglich des Umgangs mit der Website bzw. verweist auf deren Funktionen wie beispielsweise das Verschieben der Regler. Zur Sicherung der Ergebnisse und Förderung des intermodalen Transfers werden die auf der Website eingestellten Aufgaben in analoge Malkreuz-Vorlagen übertragen. Ziel ist es, dass der Schüler bzw. die Schülerin erkennt und auch mündlich kommuniziert, dass das Malkreuz bei allen Malaufgaben funktioniert und beliebige Teilmalaufgaben gebildet werden können, ohne dass sich die Anzahl der Rechtecke im Rechteckgitter bzw. das Ergebnis der Ausgangsmalaufgabe ändert. Diese Kommunikation zwischen dem Schüler bzw. der Schülerin und der Lehrperson über die Allgemeingültigkeit des, wenn auch nicht namentlich benannten, Distributivgesetzes stellt den Abschluss der Lernumgebung dar.

Die praktische Umsetzung der Lernumgebung kann durchaus auch über die Eins-zu-eins-Situation hinausgehen und in größeren Lerngruppen erfolgen. Dabei ergeben sich wiederum verschiedene Möglichkeiten, Phasen des Austauschs zwischen den Schülerinnen und Schülern umzusetzen.

Potenzial des Einsatzes (digitaler) Medien

Materialeinsatz:

Investiver Materialeinsatz:

vorgefertigtes Malkreuz (s. unten) (selbst erstellt unter Nutzung des Tafelbildes von Pixabay)

Malwinkel

Holzspieße als "Kreuz"

Tablet mit Touchfunktion/Computer/PC (aufgeladen) mit Internetzugang, ggf. Computermaus

Website „Partial Product Finder“: https://apps.mathlearningcenter.org/partial-product-finder/ [letzter Zugriff: 14.08.2021].

Konsumtiver Materialeinsatz:

400er Punktefeld (s. unten) (selbst erstellt)

Buntstifte

Radiergummi

weiße, leere Blätter

Arbeitsblätter mit Malkreuzvorlagen (s. unten) (selbst erstellt)

Bilder der Materialien:

Vor- und Nachteile der Arbeitsmaterialien/Materialorganisation:

Grundsätzlich sind alle verwendeten Materialien entweder standardmäßig im Klassenzimmer vorhanden bzw. ohne großen Aufwand zu organisieren oder selbst zu erstellen. Eine mögliche Schwierigkeit stellt je nach Ausstattung der Schule bzw. Gruppengröße der digitale Materialaufwand dar, wenn im Klassenkontext jeder Schüler bzw. jede Schülerin mit einem digitalen Endgerät versorgt werden muss. Angesichts dessen, dass in der Lernumgebung zunächst mit dem bereits bekannten Punktefeld gearbeitet wird und erst im Anschluss das womöglich unbekannte Rechteckgitter zum Einsatz kommt, bereitet die Darstellungsform des Rechteckgitters weniger Schwierigkeiten, als wenn ausschließlich mit dem Rechteckgitter gearbeitet werden würde bzw. das Rechteckgitter zeitlich vor dem Punktefeld zum Einsatz kommen würde. Der zentrale Vorteil des Einsatzes der Website liegt darin, dass sehr effizient und differenzierend gearbeitet werden kann, indem in kurzer Zeit neue Malaufgaben und Teilmalaufgaben generiert werden können und der Zahlenraum beliebig variiert werden kann. Die Effizienz des digitalen Handelns setzt allerdings voraus, dass die Lernenden, im Falle der Arbeit mit einem Laptop oder Computer, über entsprechende motorische Fähigkeiten im Umgang mit einer Computermaus verfügen. Bezüglich des analogen Materials ergibt sich beim 400er Punktefeld der Nachteil, dass je nach gewählter Darstellungsform der Teilmalaufgaben das Punktefeld nicht mehr für weitere Zerlegungen der gleichen Malaufgabe bzw. andere Malaufgaben verwendet werden kann, da beispielsweise mit Buntstiften entsprechende aufgabenbezogene Markierungen vorgenommen wurden. Um das „Preis-Leistungs-Verhältnis“ der Lernumgebung zu verbessern, wäre es dahingehend eine Möglichkeit, das Punktefeld zu laminieren und die Markierungen mit wasserlöslichen Folienstiften vorzunehmen. In diesem Fall könnte das Punktefeld auch in anderen mathematischen Kontexten eingesetzt werden.

Fachdidaktisches Potenzial der Arbeitsmittel:

Das fachdidaktische Potenzial des Rechteckgitters gegenüber dem Punktefeld liegt darin, dass dieses in höheren Klassenstufen genutzt werden kann, wenn der Zahlenraum erweitert wird und beispielsweise Bruchzahlen thematisiert werden (vgl. Wittmann, 1997, S. 50). Das analoge 400er Punktefeld ist bewusst so gestaltet, dass die Kraft der 5 und Kraft der 10 ersichtlich wird und so die Ablösung vom zählenden Rechnen unterstützt und die (quasi-)simultane Zahlerfassung gefördert wird (vgl. Krauthausen, 2018, S. 334). Sowohl das Rechteckgitter als auch das Punktefeld fördern darüber hinaus durch die strukturierte Zahldarstellung die Grundvorstellung der Multiplikation als verkürzte Addition (vgl. Krauthausen, 2018, S. 334).

Funktionen der Arbeitsmittel:

Das 400er Punktefeld sowie das Rechteckgitter der Website „Partial Product Finder“ stellen selbst keinen Lerninhalt dar, sondern erfüllen in der Lernumgebung folgende Funktionen (vgl. Krauthausen, 2018, S. 327 - 333): Die Arbeitsmittel dienen der ikonischen Darstellung einer Zahl, speziell dem Ergebnis einer Multiplikationsaufgabe, sprich eines Produktes. Zudem können an dem Material die Rechenoperationen, die in einem Malkreuz vorgenommen werden, visuell veranschaulicht und damit besser nachvollzogen werden. Darüber hinaus können die Materialien als Argumentations- und Beweismittel genutzt werden, indem erkannt wird, dass sich die Anzahl der Punkte bzw. Rechtecke nicht durch das Bilden von Teilmultiplikationsaufgaben verändert.

Notwendige Zuwendung der Lehrperson:

Mit Ausnahme der Website „Partial Product Finder“ werden in der Lernumgebung den Schülerinnen und Schülern aus dem Unterricht bekannte Arbeitsmittel eingesetzt. Beim Umgang mit der Website bzw. dem digitalen Endgerät ist in der Eins-zu-eins-Situation ggf. eine Unterstützung durch die Lehrperson notwendig, wenn die Bedienung Schwierigkeiten bereitet. Bei der Durchführung im Klassenkontext ist eine Eins-zu-eins-Betreuung zwischen Lehrperson und Schülerinnen und Schülern hingegen nicht möglich, wobei sich dahingehend Austauschphasen zwischen den Schülerinnen und Schülern eignen, um die geringeren Zuwendungskapazitäten der Lehrperson auszugleichen. Hinsichtlich des Beweisprozesses selbst steht die Lehrperson in der Eins-zu-eins-Situation durchgehend als Gesprächspartner/-in zur Verfügung, achtet aber dennoch darauf, dass nicht zu stark gelenkt und stattdessen im Sinne des Scaffolding ein "Gerüst" in Form von Impulsen, Fragen bzw. Hilfestellungen bereitgestellt wird (vgl. Brunner, 2014, S. 93). Bei fehlender Eins-zu-eins-Betreuung im Klassenkontext sind in diesem Zusammenhang diskursive Klassengespräche denkbar.

Evaluation

Strategiedokumente:

Die Schülerinnen und Schüler haben in der Lernumgebung die Möglichkeit, individuelle Rechenwege, Notizen oder Skizzen auf weißen Blättern festzuhalten, die wiederum als Strategiedokumente fungieren können. Weiterhin können ggf. die Arbeitsblätter mit den Malkreuz-Vorlagen als Strategiedokumente herangezogen werden. Dabei können Vorgehensweisen bei der Zerlegung der Faktoren in Summanden ersichtlich werden, die sich beispielsweise im wahllosen Zerlegen der Faktoren oder in systematischen Herangehensweisen wie dem gegensinnigen Verändern zeigen.

Förderimpulse:

Ausgehend von den Strategiedokumenten können beispielsweise fehlerhafte Umsetzungen von bestimmten Rechenstrategien erkannt werden, die sich zum Beispiel in der fehlerhaften Notation des Übertrags zeigen. Beim Ausfüllen der Malkreuz-Vorlagen kann festgestellt werden, ob die Schülerinnen und Schüler über ein entsprechend ausgeprägtes Stellenwertverständnis verfügen oder ob zum Beispiel ziffernweise gerechnet wird. Darüber hinaus können auch durch die Beobachtung bzw. die Analyse der Aussagen der Schülerinnen und Schüler mögliche Förderimpulse abgeleitet werden. Beispielsweise zeigt sich in der Lernumgebung, ob die Lernenden das Kleine Einmaleins sicher beherrschen bzw. wie diese Malaufgaben gelöst werden. In diesem Zusammenhang kann zum Beispiel beobachtet werden, wie viel Zeit für das Lösen von Einmal-eins-Aufgaben benötigt wird und ob im Kopf oder zählend mit den Händen gerechnet wird.

Anerkennung:

Analog zur Ableitung der Förderimpulse können anhand der Strategiedokumente sowie Äußerungen und Beobachtung der Schülerinnen und Schüler durch die Lehrperson anerkennenswerte Schülerlösungen identifiziert werden.

Soziales Lernen:

Insbesondere bei der Durchführung der Lernumgebung mit mehr als einem Schüler bzw. einer Schülerin ergeben sich durch den gegenseitigen Austausch und gegenseitige Unterstützungsleistungen der Lernenden untereinander zahlreiche Anlässe zum sozialen Lernen.

Vernetzung mit anderen Lernumgebungen

Im Vorfeld der Durchführung der Lernumgebung sind Übungen zum Erkennen multiplikativer Strukturen am Punktefeld denkbar. Dazu wäre es möglich, die Schülerinnen und Schülern unter dem Impuls „Finde Malaufgaben im Punktefeld“ verschiedene Malaufgaben im Punktefeld markieren zu lassen und so die Vorstellung der flächigen Darstellung der Multiplikation zu fördern (vgl. Technische Universität Dortmund, 2019, S. 2).

Im Sinne des Spiralcurriculums bietet die Lernumgebung Anknüpfungspunkte, um in höheren Klassenstufen die binomischen Formeln mathematisch herzuleiten (vgl. Selter & Zannetin, 2018, S. 55; Wittmann, 1997, S. 53). Dabei würden sich, wie im Beispiel dargestellt, im Fall der 1. Binomischen Formel zwei quadratische Felder im Punktefeld bzw. dem Rechteckgitter ergeben. Ausgehend von konkreten Zahlenbeispielen können zur Verallgemeinerung die Variablen a und b eingeführt werden.

Außerdem ermöglicht die Verwendung von Rechteckgittern anstelle von Punktmustern den Transfer auf Bruchzahlen, die in den weiterführenden Schulen thematisiert werden (vgl. Wittmann, 1997, S. 50). Zudem kann ein Bezug zur Geometrie hergestellt werden, wenn es um die Berechnung von Flächeninhalten geht. Die Verwendung des Rechteckgitters ermöglicht in diesem Zusammenhang das Arbeiten mit Einheitsquadraten.

Ein Bezug zur außerschulischen Lebenswelt ergibt sich durch die thematische Einbettung der Lernumgebung, welche das Themenfeld „Studium“ aufgreift. Durch die Darstellung der Geschichte im Einstieg wird den Schülerinnen und Schülern vermittelt, dass Verständnisschwierigkeiten im schulischen bzw. bildungsbezogenen Kontext „normal“ sind und durch intensive inhaltliche Auseinandersetzung überwunden werden können.

Reflexion der Lernumgebung

Folgende Stolpersteine könnten bei der Durchführung der Lernumgebung auftreten:

Angesichts dessen, dass in der Lernumgebung eine Website eingesetzt wird, wobei ein Internetzugang unabdingbar ist, können Technikausfälle dazu führen, dass das digitale Material nicht genutzt werden kann. In einem solchen Fall kann alternativ auch auf das analoge 400er Punktefeld zurückgegriffen werden. Zur Anwendung bei mehreren Malaufgaben sollte dieses laminiert sein und wasserlösliche Folienstifte verwendet werden. Hierbei ergeben sich allerdings Einschränkungen bezüglich der Variabilität des Zahlenraums, da dieser am verwendeten Punktefeld auf maximal 400 beschränkt ist. Darüber hinaus sollte der angemessene Umgang mit dem digitalen Endgerät vorab geklärt werden und insbesondere im Klassenkontext, wenn eine Eins-zu-eins-Betreuung nicht gewährleistet werden kann, festgelegt werden, dass ausschließlich Aktivitäten auf der Website „Partial Product Finder“ stattfinden und keine anderen Internetseiten von den Schülerinnen und Schülern aufgerufen werden. Angesichts dessen, dass das Beweisen an sich eine sehr komplexe und kognitiv anspruchsvolle Tätigkeit darstellt und die Lehrperson im Austausch mit dem Schüler bzw. der Schülerin spontan auf dessen bzw. deren Äußerungen und Lösungsansätze reagieren muss, besteht gerade bei ungeübten Durchführenden die Gefahr, dass mit weniger lernförderlichen Impulsen reagiert oder auch zu stark gelenkt wird.

Die Anwendung der Lernumgebung gestaltet sich problematisch und sollte vermieden werden, wenn das Stellenwertverständnis noch nicht ausreichend entwickelt ist und beispielsweise mit Ziffern statt mit Zahlen im Malkreuz gerechnet wird.

Nach der Durchführung

Daten zur Durchführung

Die Lernumgebung wurde in dieser Form noch nicht durchgeführt.

Literatur

Brunner, E. (2014). Mathematisches Argumentieren, Begründen und Beweisen. Grundlagen, Befunde und Konzepte. Berlin, Heidelberg: Springer Spektrum.

Freudenthal, H. (1974). Die Stufen im Lernprozess und die heterogene Lerngruppe im Hinblick auf die Middenschool. Neue Sammlung, 14, 161 - 172.

Käpnick, F. & Benölken, R. (2020). Mathematiklernen in der Grundschule (2. Auflage). Berlin: Springer Spektrum.

KMK (2004). Bildungsstandards im Fach Mathematik für den Primarbereich. Beschluss vom 15.10.2004. München, Neuwied: Wolters-Kluwer, Luchterhand Verlag.

Krauthausen, G. (2018). Einführung in die Mathematikdidaktik – Grundschule (4. Auflage). Berlin: Springer Spektrum.

Meyer, M. & Prediger, S. (2009). Warum? Argumentieren, Begründen, Beweisen. Praxis der Mathematik in der Grundschule, 51(30), 1 - 7.

Scherer, P. & Moser Opitz, E. (2010). Fördern im Mathematikunterricht der Primarstufe. Heidelberg: Spektrum Akademischer Verlag.

Selter, C., Prediger, S., Nührenbörger, M. & Hußmann, S. (2014). Mathe sicher können. Handreichungen für ein Diagnose- und Förderkonzept zur Sicherung mathematischer Basiskompetenzen. Natürliche Zahlen. Berlin: Cornelsen Schulverlage GmbH.

Selter, C. & Zannetin, E. (2018). Mathematik unterrichten in der Grundschule. Seelze: Kallmeyer.

Technische Universität Dortmund (2019). Operationsvorstellungen Multiplikation – Punktebilder. Online verfügbar unter: https://pikas-kompakt.dzlm.de/sites/pikaskp/files/uploads/07-OperationsvorstellungenMultiplikation/opvmulti_punktebilder.pdf [Zugriff: 29.06.2021].

Wittmann, E. C. (1997). Von Punktmustern zu quadratischen Gleichungen. Mathematik lehren, 83, 50 - 53.

Wittmann, E. C. (2014). Operative Beweise in der Schul- und Elementarmathematik. mathematica didactica, 37, 213 - 232.