Benutzer:Snark~dewikiversity/Ungleichverteilungsmaße

Ungleichverteilungsmaße beschreiben den Grad der Ungleichverteilung einer Größe gegenüber einer anderen Größe. In den Sozialwissenschaften sind diese Größen auf der einen Seite häufig Ressourcen wie Einkommen oder Vermögen und auf der anderen Seite die Anzahl derer, die über Einkommens- und Vermögensanteile verfügen. Mit Ungleichverteilungsmaßen wird angegeben, zu welchem Grad die Zuordnung von Ressourcen zu Menschen von einer Gleichverteilung abweicht. Im Folgenden wird ein kurzer Überblick über die wichtigsten Ungleichverteilungsmaße gegeben.

Mit Ungleichverteilungsmaßen sind keine direkten Wertungen verbunden. Die Wertungen ergeben sich aus der Empirie. Ob ein konkretes Ungleichverteilungsmaß „zu hoch“ oder „zu niedrig“ ist, ergibt sich aus dem Vergleich von Ressourcen-Ungleichverteilungen mit Lebensqualitäten. Dabei muss berücksichtigt werden, dass Lebensqualitäten von vielen weiteren Faktoren mitbestimmt werden.

Drei wichtige Ungleichverteilungsmaße

Ungleichverteilungsmaße geben an, wie groß der Abstand einer gegebenen Verteilung zur Gleichverteilung ist, wobei das Erreichen der Gleichverteilung kein normativ erklärtes Ziel ist, sondern nur ein Referenzpunkt bei der Berechnung. Als einfachstes Ungleichverteilungsmaß basiert die Hoover-Ungleichverteilung auf einer Verteilung, bei der eine Ungleichverteilung in eine Gleichverteilung zu jeder Zeit voll informiert überführt wird. Diese Bedingung ermöglicht auf dem Weg zur Gleichverteilung die gesteuerte Minimierung der Bewegung von Ressourcen. Damit ist das Verteilungsmodell planwirtschaftlich. Demgegenüber liegt dem Theil-Index das Verteilungsmodell einer völlig ungeregelten Wirtschaft zugrunde, in dem die Umverteilung in einem rein stochastischen Prozess erfolgt. Zu keiner Zeit werden bei diesem Modell von den darin wirkenden Akteuren und Prozessen irgendwelche Informationen über die aktuelle Ressourcenverteilung ausgewertet. Zwar kommt der Theil-Index zunehmend häufiger zum Einsatz, jedoch wird der Gini-Koeffizient immer noch am häufigsten verwendet. Er ist eine Auswertung der Lorenzkurve und wirkt damit zwar anschaulicher als andere Ungleichverteilungsmaße, aber ihm lag bei seiner Entwicklung kein Verteilungsmodell zugrunde.

Hoover-Ungleichverteilung

Theil-Index $T$ und Hoover -Ungleichverteilung $H$:
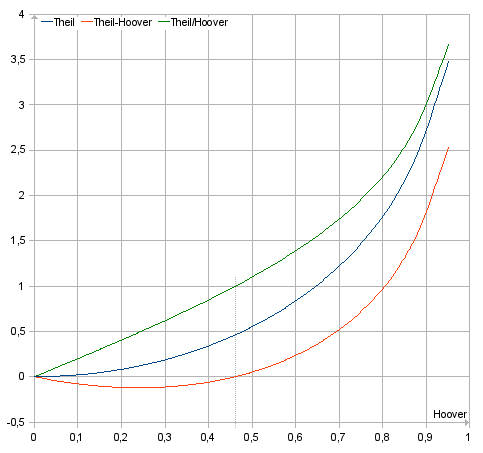
Die Grafik illustriert den Verlauf von T, T-H und T/H als Funktion von $H$ für Gesellschaften, die in zwei Quantile aufgeteilt sind, in denen ein Anteil von $a$ Euro einem Anteil von $b$ Menschen zugeordnet ist und ein Anteil von $b$ Euro einem Anteil von $a$ Menschen zugeordnet ist, wobei $a+b=1$ gilt (z. B. das „80:20 Pareto-Prinzip“ mit $A=0{,}8$ und $B=0{,}2$, woraus $H=0{,}6$ und $T=0{,}832$ resultiert). Für derart partitionierte Gesellschaften, sind der Theil-Index und der symmetrierte Theil-Index gleich. Einen gleichen Verlauf nehmen auch der Gini-Koeffizient $G$ und die Hoover-Ungleichverteilung $H$. Unter diesen Voraussetzungen gilt T = 2 H artanh(H).

Verteilung und hervorgehobene Punkte:
- Bei 50:50 nehmen T und $H$ den Wert 0 an.
- Bei etwa 62:38 wird für T-H ein Minimum erreicht.
- Bei etwa 73:27 nehmen T und $H$ den gleichen Wert an (etwa 0,46).
- Bei etwa 80:20 erreicht T den Wert 0,832 („Pareto-Prinzip“).
- Bei etwa 82:18 erreicht T den Wert 1.

Die Hoover-Ungleichverteilung ist das einfachste aller Ungleichverteilungsmaße. Die Hoover-Ungleichverteilung ist 0 (oder 0 %) bei völliger Gleichverteilung und 1 (oder 100 %) bei maximaler Ungleichverteilung. Sie gibt direkt an, welcher Anteil beispielsweise eines ungleichverteilten Gesamteinkommens bewegt werden müsste, um eine völlige Gleichverteilung zu erzielen.

Man kann mit dem Hoover-Index die Wirkung einer Steuerprogression direkt messen: Im Jahr 2004 ergab sich eine Hoover-Ungleichverteilung der Brutto-Einkommen von 0,366. Bei einer Einheitssteuer ohne Freibetrag läge auch die Ungleichverteilung der Netto-Einkommen bei 0,366. Tatsächlich ergab sich aber eine Hoover-Ungleichverteilung von 0,336. Es wurden also durch die Steuerprogression 3,0 % des Netto-Einkommens „von oben nach unten“ umverteilt.

Die Hoover-Gleichverteilung ist 1 (oder 100%) abzüglich der Hoover-Ungleichverteilung. Eine für ein Volkseinkommen mit der Hoover-Gleichverteilung berechnete Wohlfahrtsfunktion ergibt sich, wenn das Volkseinkommen mit der Hoover-Gleichverteilung multipliziert wird. Diese Wohlfahrtsfunktion hat eine konkrete Bedeutung: Sie ist der Anteil des Volkseinkommens, der unangetastet bliebe, wenn man das Volkseinkommen so umverteilen würde, dass sich eine völlige Gleichverteilung ergäbe.

Wird das Volkseinkommen mit der Hoover-Ungleichverteilung multipliziert oder wird von dem Volkseinkommen die Wohlfahrtsfunktion abgezogen, dann ergibt sich der Anteil des Volkseinkommens, der insgesamt bewegt werden müsste, wenn eine völlige Gleichverteilung mit minimalem Aufwand durchgeführt werden sollte. Dazu wäre eine perfekte Planung unter der Voraussetzung vollständiger Informiertheit erforderlich.

Theil-Index

Der Theil-Index ist ein aus der Informationstheorie abgeleitetes Ungleichverteilungsmaß. Er gehört zur Familie der Entropiemaße. Der Theil-Index wird gelegentlich fälschlicherweise auch als Theil-Entropie bezeichnet. Tatsächlich handelt es sich dabei aber um eine Redundanz, denn er ist die Differenz zwischen einer sich bei Gleichverteilung einstellenden maximalen Entropie und einer sich aus einer Ungleichverteilung ergebenden aktuellen Entropie.

Der Theil-Index ist 0 bei völliger Gleichverteilung und 1 bei einer Ungleichverteilung, bei der 17,6 % der Ressourcenbesitzer über 82,4 % der Gesamtressourcen und umgekehrt 82,4 % der Ressourcenbesitzer über 17,6 % der Ressourcen verfügen. Als Merkhilfe kann hierbei dienen, dass diese Ungleichverteilung für einen Theil-Index von 1 ziemlich nahe an der 80:20-Verteilung liegt, die als „Pareto-Prinzip“ bekannt ist. Bei einer höheren Ungleichverteilung ist der Theil-Index größer als 1.

Im Unterschied zur Hoover-Ungleichverteilung werden bei der Berechnung des Theil-Index werden nicht nur Disparitäten aggregiert, sondern diese Disparitäten werden mit ihrem Informationsgehalt gewichtet. Daraus ergibt sich dann eine Kennzahl, die nicht nur den Anteil der für einen Ausgleich umzuverteilenden Ressourcen beschreibt, sondern auch die Aufmerksamkeit, die die Ungleichverteilung hervorruft.

Den Theil-Index gibt es in zwei Ausführungen. Der Theil-L-Index beschreibt die Verteilung von Ressourcen zu Menschen, der Theil-T-Index beschreibt die Verteilung von Menschen zu Ressourcen. Der Mittelwert beider Indizes ist ein symmetrierter Theil-Index, der strukturell der einfachen Hoover-Ungleichverteilung sehr ähnlich ist (siehe Hauptartikel).

Die Normierung der Theil-Indizes in den Bereich zwischen 0 und 1 (beziehungsweise zwischen 0% und 100%) erfolgt mit der Transformation $1-e^{-T}$. Das Resultat dieser Transformation sind den drei Theil-Indizes entsprechende normierte Ungleichverteilungsmaße.

Gini-Koeffizient

Der Gini-Koeffizient ist das in den Sozialwissenschaften am häufigsten verwendete Ungleichverteilungsmaß. Er ist 0 (oder 0 %) bei völliger Gleichverteilung und 1 (oder 100 %) bei maximaler Ungleichverteilung. Seine Berechnung lässt sich sehr anschaulich mit den Mitteln der Geometrie darstellen; was ein gemessener Gini-Koeffizient jedoch sozialwissenschaftlich bedeutet, lässt sich nicht geometrisch vermitteln.

Die langjährige und häufige Verwendung des Gini-Koeffizienten führte jedoch zu einem empirischen Verständnis für die Bedeutung der Gini-Koeffizienten. Auch gibt es empirische Untersuchungen, die den Zusammenhang zwischen subjektiven Wertungen von Ungleichverteilungen und den dazugehörigen Ungleichheitsmaßen erforschen. Den Gini-Koeffizienten verwendet man zumindest dann, wenn Forschungen fortgesetzt werden sollen, in denen bereits mit diesem Ungleichverteilungsmaß gearbeitet wurde.

Tabellenkalkulation

Der Gini-Koeffizent, die Hoover-Ungleichverteilung und des Theil-Index können gemeinsam mit einer Tabellenkalkulation ermittelt werden. Der Theil-Index ist hierbei der Mittelwert aus dem Theil-Index für die Verteilung von Ressourcen auf Nutzer und dem Theil-Index für die Verteilung von Nutzer auf Ressourcen.

Gruppe	Nutzer pro Gruppe	Ressource pro Gruppe	Ressource pro Nutzer	relative Abweichung	kumulierte Ressourcen	Gini	Hoover	Theil
1	A1	E1	Ē1 = E1/A1	D1 = E1/ΣE - A1/ΣA	K1 = E1	G1 = (2·K1 - E1)·A1	H1 = abs(D1)	T1 = ln(Ē1)·D1
2	A2	E2	Ē2 = E2/A2	D2 = E2/ΣE - A2/ΣA	K2 = E2 + K1	G2 = (2·K2 - E2)·A2	H2 = abs(D2)	T2 = ln(Ē2)·D2
3	A3	E3	Ē3 = E3/A3	D3 = E3/ΣE - A3/ΣA	K3 = E3 + K2	G3 = (2·K3 - E3)·A3	H3 = abs(D3)	T3 = ln(Ē3)·D3
4	A4	E4	Ē4 = E4/A4	D4 = E4/ΣE - A4/ΣA	K4 = E4 + K3	G4 = (2·K4 - E4)·A4	H4 = abs(D4)	T4 = ln(Ē4)·D4
Summen	ΣA	ΣE	Ē = ΣE/ΣA			ΣG	ΣH	ΣT
Indizes						Gini = 1 - ΣG/ΣA/ΣE	Hoover = ΣH / 2	Theil = ΣT / 2
Wohlfahrt						WG = Ē·(1 - Gini)	WH = Ē·(1 - Hoover)	WT = Ē·e-Theil

Für die Berechnung wird eine Gesellschaft in Gruppen unterteilt, wobei in jeder Gruppe eine bestimmte Anzahl A von Nutzern zusammengefasst sind, die sich eine Gruppen-Ressource mit dem Umfang E teilen. Diese beiden Gruppenparameter müssen positiv sein. Die Gruppen-Ressource ist oft die Summe aller Einkommen in der Gruppe. Die Anzahl der Gruppen ist beliebig. In diesem Beispiel sind es vier Gruppen.

Für den Theil-Index und die Hoover-Ungleichverteilung wäre keine Sortierung der Parameterpaare A und E notwendig. Aber da hier auch der Gini-Koeffizient berechnet wird, müssen die Gruppen trotzdem sortiert werden. Die Spalte „Ressource pro Nutzer“ ist dabei das Sortier-Kriterium, nach dem in aufsteigender Reihenfolge von E die Parameterpaare A und E zu sortieren sind.

In der Tabelle sind die Felder für die Eingangsdaten gelb unterlegt. Die Ausgabefelder sind grün unterlegt. In den Ausgabefeldern liegt der Wertebereich für den Gini-Koeffizenten und die Hoover-Ungleichverteilung zwischen Null und Eins. Der Theil-Index kann bei hohen Ungleichverteilungen auch größer als Eins werden.

Andere Ungleichverteilungsmaße

In den Sozialwissenschaften gibt es etwa 50 Ungleichverteilungsmaße. Viele sind miteinander verwandt oder parallel entwickelt worden. In der gegenwärtigen Forschung werden zunehmend Entropiemaße wie der Theil-Index verwendet. In der Wikipedia existieren Hauptartikel zu diesen weiteren Ungleichverteilungs- und Konzentrationsmaßen: Atkinson-Maß, Konzentrationsmaß von Herfindahl, Rosenbluth-Index und Lerner-Index.

Anwendung

Ungleichverteilungsmaße sind Indikatoren für die Beobachtung beispielsweise von Einkommensverteilungen. Vergleichbar sind diese Maßzahlen in Zeitreihen oder beim Vergleich von Regionen, sozialen Gruppen usw. nur, wenn sie mit gleichen Methoden (z.B. gleiche Aufteilung in Quantile) berechnet wurden. Als Ergebnis der Auswertung von Datensätzen reduzieren Ungleichverteilungsmaße die Sicht des Beobachters auf eine einzelne Zahl. Solche Vereinfachungen sind dann zulässig, wenn ihre Beobachtungen schnelle Entscheidungen ermöglichen, ob die Entwicklung beobachteter Ungleichverteilungen einer genaueren Analyse bedürfen. Auch können sie Bestandteile von ökonometrischen Formeln sein. Beispiele sind die Berechnung der Wohlfahrtsfunktion, die Beobachtung der Steuerprogression und der Vorschlag, die Besteuerung mit Hilfe der Ungleichverteilung der Einkommen zu regulieren. Ungleichverteilungsmaße können den dafür erforderlichen Formelbestandteil liefern.

Quellen und Anmerkungen

[[w:en:Income inequality metrics]] [[w:Kategorie:Volkswirtschaftliche Kennzahl]] [[w:Kategorie:Einkommen]] [[w:Kategorie:Ökonometrie]]