Das große Müllauto Problem
Modellierungsthema
[Bearbeiten]Unser Modellierungsprojekt behandelt das jeden betreffende und realitätsnahe Problem, dass der Müll jeden Haushaltes möglichst ökonomisch, effizient und umweltschonend gesammelt und abtransportiert werden soll. Ein Müllauto soll auf kürzestem Weg alle Mülleimer in einem abgeschlossenen Gebiet in Kaiserslautern leeren. Hierbei wollen wir den Weg des Müllautos optimieren und die Zeit der Leerung durch die Modellierung des Fahrtweges optimal berechnen.[1]

Mögliche einzuholende Daten
[Bearbeiten]Um eine möglichst realitätsnahe Modulation und Optimierung zu gewährleisten, wollen wir folgende Daten von einem Entsorgungsunternehmen einholen:
- wie viele Mülltonnen gibt es pro Straße?
- wie viele Mülltonnen gibt es in dem Gebiet?
- wie groß ist die Kapazität des Müllautos?
- wie schnell können die Tonnen geleert werden?
- wie viel Müll passt in eine Mülltonne? (Volumen)
- wie weit ist die Reichweite eines Müllautos?
- Kartenmaterial der Region -> Straßenlängen, Sackgassen, ...
- wie sind die Arbeitszeiten (Mittagspause) des Betriebes/der Mitarbeiter?
- Wo liegt der Startpunkt der Müllautos?
- Wo befindet sich die Entsorgungsstelle für den gesammelten Müll?
- Wie groß ist der Spritverbrauch des Fahrzeuges?
Ziele
[Bearbeiten]
- Erleichterung der Arbeit der Müllabfuhr Kaiserslautern
- Wegoptimierung und Zeitersparnis der Arbeiter
- Mathematische Berechnung des kürzesten Weges
- Steigerung der Effizienz des Betriebes
- Kostenoptimierung/Kostenminimierung
Beispiel 1
[Bearbeiten]Im Bild [2] ist der günstigste Pfad zwischen den Knoten und der Pfad, welcher in startet, und über nach geht. Die Pfadkosten betragen in dem Beispiel . Will man einen Pfad von nach finden, so ist der direkte Weg mit Kosten von nicht der bestmöglichste Pfad, da der Weg von über nach nur "Kosten" von hat.
Beispiel 2 (mit Schulbezug)
[Bearbeiten]

Das Pizza-Hut-Restaurant befindet sich in Magdeburg in der Kantstraße (Knoten a). Von dort aus werden auch Bestellungen außer Haus geliefert. Der Graph links zeigt Adressen, zu denen ein Pizza-Bote die Bestellungen bringen soll. Die Kantenbewertungen stellen die Entfernungen zwischen den Knoten (Punkten) in Kilometer dar. Ziel ist es den kürzesten Weg von Knoten a zum Knoten d zu finden.[3]
Die kürzeste Verbindung eines Knotens zum Startknoten a verläuft wie im Graph rechts auf den grünen Kanten. Vom Knoten a zum Knoten d beträgt die kürzeste Verbindung 2 km.[4]
Führt man dieses Problem weiter und fragt danach, ob es in einem Graphen eine „Rundreise“ gibt, bei der jede Kante genau einmal „durchlaufen“ wird und man auch wieder zum Ausgangspunkt zurückkehrt, ist dies die Frage nach einem speziellem Rundweg – dem Eulerkreis.
Das Finden eines Eulerkreises auf einem Graphen könnte mit den Schülerinnen und Schülern ebenfalls algorithmisch gelöst werden.
Niveauzuordnung
[Bearbeiten]Sek 1
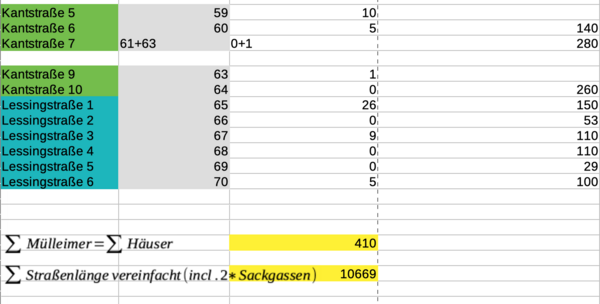
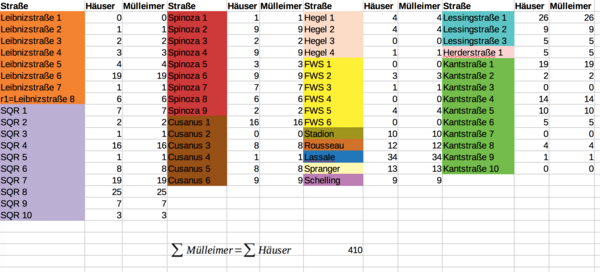
[Bearbeiten]- Datenauswertung (Straßenlänge, Häuser-Anzahl, Mülleimer-Anzahl)
- Erstellung eines Graphen in Geogebra (Straßennetz)
- Daten in Excel übertragen und einpflegen
- einen kurzen Weg mathematisch ausprobieren durch verschiedene Weg-Kombinationen zu einem möglichst kurzen Weg gelangen
- verschiedene Wege mit Excel berechnen und diese bezüglich ihrer Länge vergleichen (kürzester Weg schließt Projekt ab)
Sek 2
[Bearbeiten]- Herausfiltern, welche Straßen wirklich befahren werden müssen (weil Mülleimer geleert werden müssen) oder nur als Durchfahrtsstraße dienen, sodass nicht mehr alle Straßen abgefahren werden müssen (mit Hilfe von Excel und Geogebra)
- mit Programm GeoGebra das Netzwerk der Straßen nachbilden
Uni
[Bearbeiten]- einen automatisierten Algorithmus mit Python programmieren
- Verbesserung des Algorithmus
Modellierungszyklen
[Bearbeiten]Zyklus 1
[Bearbeiten]Zielsetzung:
[Bearbeiten]Auswertung von Kartenmaterial:
Ziel des ersten Zyklus ist es zunächst, in einer Karte einen Bereich aus zu wählen, der mindestens 10 Straßen enthält, die von der Müllabfuhr abgefahren werden sollen. Dabei wollen wir anschließend auf die Anzahl der Mülltonnen pro Straße (bzw. im ganzen Gebiet) und deren Füllmenge, die Kapazität des Müllautos und die Länge der Straßen, eingehen. Auch soll der Start- und Entsorgungspunkt des Müllautos eine Rolle spielen.
Diese Informationen sollen alle aus einer Karte entnommen werden und in einer Exceltabelle zu einer Lösung führen.
Die Tabelle soll die Parameter Anzahl der Mülltonnen und deren Füllmenge, die Kapazität des Müllautos und die Länge der Straßen beinhalten.
Daraufhin soll die schnellst mögliche Strecke durch das Straßennetz der Karte gefunden werden.
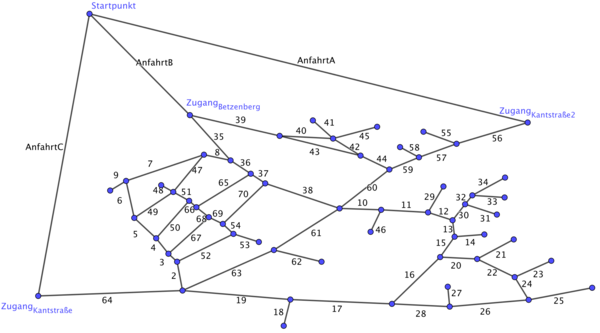
Der Verlauf der Straßen soll deshalb in einem Graph mit Knoten für die Kreuzungen festgehalten werden, womit man ein mögliches Abfahren der Straßen skizziert.
→ Mögliche Software: Tabellenkalkulation (Excel), Google Maps, GeoGebra, GraphTea (von uns nicht verwendet)
Bildmaterial der Vorarbeiten:
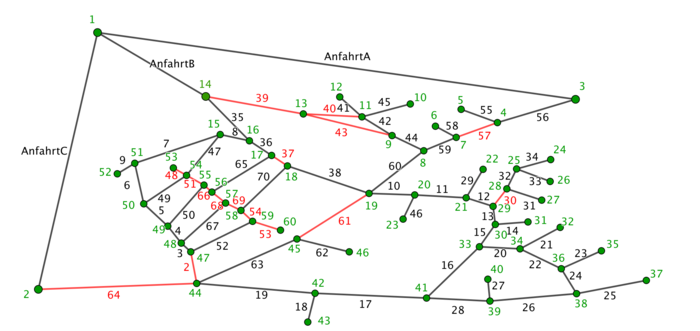
[Bearbeiten] Karte des Betzenbergs in Kaiserslautern in der die Häuser den Straßen zugeordnet wurden
Karte des Betzenbergs in Kaiserslautern in der die Häuser den Straßen zugeordnet wurden



Erläuterung Zyklus 1
[Bearbeiten]In Zyklus 1 haben wir mit Hilfe von Satellitenbildern und der Seite Google Maps ein Graphennetzwerk mit dem Programm Geogebra erstellt und die Kanten in verschiedenen Ausführungen beschriftet:
- Kantenbeschriftung mit der Anzahl der Mülleimer (welche wir vereinfacht haben, indem jedem Haus ein Mülleimer zugeordnet wurde)
- Kantenbeschriftung mit der Straßenlänge (ermittelt mit der Routenfunktion bei Google Maps)
- Kantenbeschriftung mit Zahlen von 1-69, um jedem Straßenabschnitt eindeutig zu bestimmen
In der Tabellenkalkulation haben wir ebenso die ganzen Daten verankert, um damit dann die Länge der möglichen Wege berechnen zu können. In Zyklus 1 haben wir beschlossen die Kapazität des Müllautos, sowie Spritverbrauch, Anzahl der Stops und Leerung des Müllautos nicht zu beachtet. Ein Hauptgrund dafür ist, dass wir vom zuständigen Unternehmen erfahren haben, dass die Mülleimer im Gebiet Betzenberg komplett mit einmal Abfahren geleert werden können. Außerdem haben wir die Anzahl der Mülleimer nicht benötigt, sondern vorerst nur die Straßenlänge bei unseren Berechnungen zur Hilfe genommen.
Anschließend haben wir 10 verschiedenen Wege mit je 3 verschiedenen Zufahrtswegen berechnet, sodass alle Kanten abgefahren werden (wenn nötig auch mehrmals) und haben dort einen kürzesten Weg herausgefiltert.
Damit ist der erste Zyklus beendet. Weg 10 ist der bisher kürzeste Weg, den wir herausgefunden haben mit 11770 Metern.
Aufgetretene Probleme
[Bearbeiten]- es müssen nicht unbedingt alle Straßen abgefahren werden (denn nicht an jeder Kante steht ein Mülleimer) -> Verbesserung für Zyklus 2: Straßennummer markieren, welche nicht befahren werden müssen, aber befahren werden dürfen
- Einfahrt & Ausfahrt können verschieden gewählt werden für einen kürzesten Weg -> So muss man nicht unbedingt zurück zum Ausgangspunkt
- Wir haben nur 10 Wege durchgespielt. Es ist anzunehmen, dass es noch viele weitere Möglichkeiten gibt, bei denen mit Sicherheit ein kürzerer Weg dabei ist (Idee: Wir suchen eine Funktion/ ein Programm, die dieses Verfahren vereinfachen kann)
Zyklus 2
[Bearbeiten]Zielsetzung
[Bearbeiten]Ziel des zweiten Zyklus ist es zunächst, die Straßen herauszufiltern, die nicht befahren werden müssen bzw. bei denen keine Mülleimer geleert werden müssen. Die Anzahl der Straßen, die abgefahren werden müssen, wird so reduziert, und damit auch die Gesamtstrecke die abgefahren werden muss. Außerdem wird nun angenommen, dass das Gebiet Betzenberg nicht zwingend über den gleichen Punkt wieder verlassen werden muss, an dem man in das Gebiet eingefahren ist. Der Weg kann so eventuell auch nochmal reduziert werden. Im nächsten Schritt werden - wie im Zyklus 1 - verschiedene Wege pro Anfahrt unter den neuen Voraussetzungen durchgespielt. Dabei kann ein Weg mit der bisher kürzesten Strecke herausgefunden werden.
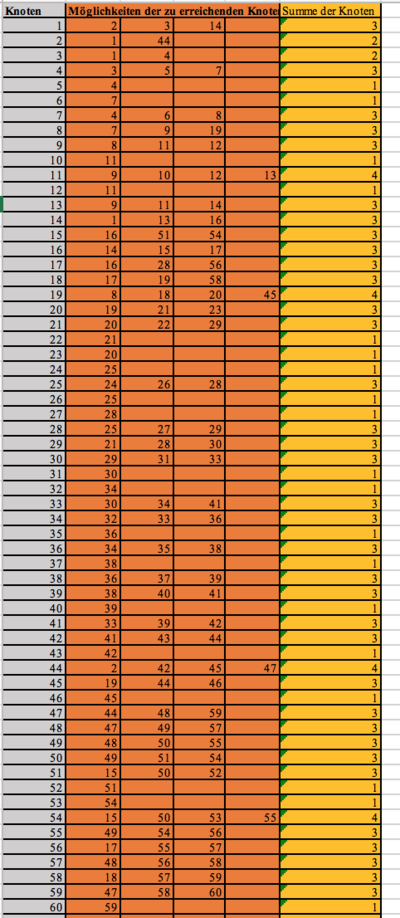
Ein weiterer Schritt liegt darin, dass wir die Knotenpunkte mit Zahlen benennen. Mit dieser Information können wir dann anschließend weiterarbeiten. Ziel ist es ein Programm zu erstellen, dass für uns durch Ausprobieren den kürzesten Weg herausfiltert.
-> Mögliche Software: GeoGebra, Libre Office (Excel), Python
Bildmaterial
[Bearbeiten]Skript Python
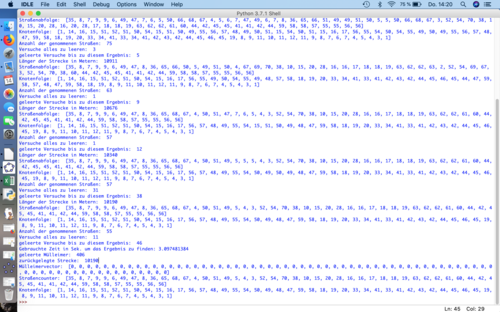
[Bearbeiten]Im folgenden Skript haben wir die Straßennummerierungen, Knotenpunkte und Straßenlänge in Vektoren gepackt, um damit anschließend alle möglichen Wege bei jedem Knotenpunkt festgelegt. Das Programm wählt an den Knoten, die unsere Kreuzungen darstellen, zufällig eine Straße, die nicht die gerade entlanggefahrene Strecke ist, aus. Jedem einzelnen Knoten wurde die Information gegeben, welchen weiteren Knoten man über welche Straße erreicht. Dies wird dann per Zufall so oft durchgespielt, bis ein akzeptables Ergebnis erreicht wird.
Ideen, um das Programm zu beschleunigen bzw. zu optimieren
[Bearbeiten]- Die Straßen, die noch zu leeren sind, sollen vor denen, die schon geleert wurden, favorisiert werden.
- Wenn alle Straßen, die an den aktuellen Knoten grenzen, schon geleert wurden, soll der angrenzende Knoten gewählt werden, der zur nächsten noch zu leerenden Straße führt.
- Sackgassen sollen direkt geleert werden, falls dort noch nicht geleert wurde.
Das Programm mit Beispielknoten
[Bearbeiten]from random import*
def Durchlauf_ueber_Anfahrt_A():
VectorMülleimer = [0,1,2,3,4,19,1,6,7,2,1,16,1,8,19,25,7,3,1,9,2,9,3,9,7,6,2,16,0,8,1,8,9,4,4,0,1,0,3,1,0,4,0,10,12,34,3,10,9,0,5,0,0,19,2,0,14,10,5,0,4,1,0,26,0,9,0,0,5]
VectorStrasse = [32,64,72,75,76,350,62,80,190,74,54,110,63,170,200,260,100,97,37,94,68,94,63,97,140,83,76,160,27,73,60,74,140,180,80,57,190,220,100,400,130,180,150,230,150,180,80,120,120,58,160,61,100,91,150,36,62,350,140,150,84,130,260,150,53,110,110,29,100]
Straßencounter = []
Knotenfolge = []
Knoten = 3
Strecke = 0
geleerteMülleimer = 0
Straße = 0
letzterKnoten = 1
aktuellerKnoten = 3
counter = 0
vorletzterKnoten = 0
vorvorletzterKnoten = 0
.
.
.
elif aktuellerKnoten == 4:
if letzterKnoten == 3:
Kreuzung = randint(1,2)
if Kreuzung == 1:
aktuellerKnoten = 5
letzterKnoten = 4
Straße = 55
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
elif Kreuzung == 2:
aktuellerKnoten = 7
letzterKnoten = 4
Straße = 57
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
elif letzterKnoten == 7:
Kreuzung = randint(1,2)
if Kreuzung == 1:
aktuellerKnoten = 5
letzterKnoten = 4
Straße = 55
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
elif Kreuzung == 2:
aktuellerKnoten = 3
letzterKnoten = 4
Straße = 56
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
elif letzterKnoten == 5:
Kreuzung = randint(1,2)
if Kreuzung == 1:
aktuellerKnoten = 7
letzterKnoten = 4
Straße = 57
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
elif Kreuzung == 2:
aktuellerKnoten = 3
letzterKnoten = 4
Straße = 56
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
elif aktuellerKnoten == 5:
aktuellerKnoten = 4
letzterKnoten = 5
Straße = 55
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
.
.
.
Straßencounter.append(Straße)
Knotenfolge.append(aktuellerKnoten)
Allesleer = all(x == 0 for x in VectorMülleimer)
return (geleerteMülleimer, Strecke, VectorMülleimer, Allesleer, Straßencounter, Knotenfolge, counter)
def b ():
Allesleer = False
Versuche_um_alles_zu_leeren = 0
while Allesleer != True:
Versuche_um_alles_zu_leeren = Versuche_um_alles_zu_leeren + 1
geleerteMülleimer, Strecke, VectorMülleimer, Allesleer, Straßencounter, Knotenfolge, counter = Durchlauf_ueber_Anfahrt_A()
return (geleerteMülleimer, Strecke, VectorMülleimer, Allesleer, Straßencounter, Knotenfolge, counter, Versuche_um_alles_zu_leeren)
def c ():
Streckenversuch = 50000
kleinste = 50000
while Streckenversuch >= 13000:
geleerteMülleimer, Strecke, VectorMülleimer, Allesleer, Straßencounter, Knotenfolge, counter, Versuche_um_alles_zu_leeren = b()
Streckenversuch = Strecke
if kleinste >= Streckenversuch:
kleinste = Streckenversuch
print('Länger der Strecke in Metern: ', Streckenversuch)
print('Straßenabfolge: ', Straßencounter)
print('Zähler der Versuche um das Ergebnis zu erhalten: ', counter)
print('Versuche alles zu leeren: ', Versuche_um_alles_zu_leeren)
print('geleerte Mülleimer: ', geleerteMülleimer)
print('zurückgelegte Strecke: ', Strecke)
print('Mülleimervector: ', VectorMülleimer)
print('Straßencounter: ', Straßencounter)
print('Knotenfolge: ', Knotenfolge)
Zyklus3
[Bearbeiten]Vereinfachtes Modell
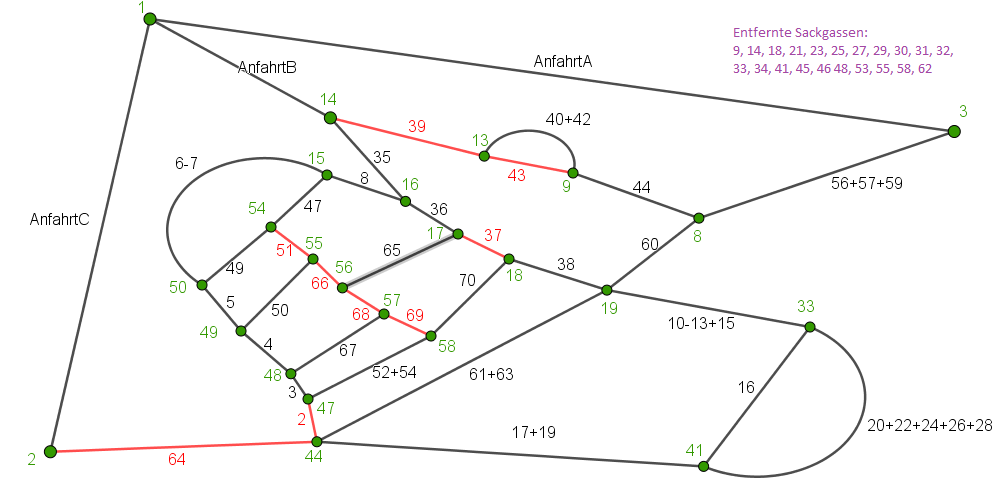
[Bearbeiten]Das bisherige Modell ist für das aktuelle Programm zu komplex, weshalb es sehr lange braucht um ein annähernd geringes Ergebnis auszugeben. Um dies zu vereinfachen, werden in einem weiteren Modell alle Sackgassen entfernt, da diese nur auf eine bestimmte Art und Weise abgefahren werden können und somit für das Endergebnis uninteressant sind. Ziel ist es somit, schneller eine Lösung zu finden.
Das Programm, welches die Sackgassen direkt anfährt, wenn diese noch nicht geleert wurde, gibt nun folgende Ausgabe in wesentlich kürzerer Zeit aus. Dazu trägt auch bei, dass das Programm bei jedem Knoten schaut, ob eine ungeleerte Straße angrenzt, die noch nicht befahren wurden, und die damit gegenüber den geleerten Straßen präferiert wird.
Eine Knotenimplementation sieht nun wie folgt aus:
elif aktuellerKnoten == 4:
if letzterKnoten == 3:
if VectorMülleimer[55-2] != 0:
Kreuzung = 1
if VectorMülleimer[57-2] != 0:
Kreuzung = 2
if VectorMülleimer[55-2] == 0 and VectorMülleimer[57-2] == 0:
Kreuzung = 2
if Kreuzung == 1:
aktuellerKnoten = 5
letzterKnoten = 4
Straße = 55
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
if Kreuzung == 2:
aktuellerKnoten = 7
letzterKnoten = 4
Straße = 57
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
elif letzterKnoten == 7:
if VectorMülleimer[56-2] != 0:
Kreuzung = 2
if VectorMülleimer[55-2] != 0:
Kreuzung = 1
if VectorMülleimer[55-2] == 0 and VectorMülleimer[56-2] == 0:
Kreuzung = 2
if Kreuzung == 1:
aktuellerKnoten = 5
letzterKnoten = 4
Straße = 55
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
if Kreuzung == 2:
aktuellerKnoten = 3
letzterKnoten = 4
Straße = 56
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
elif letzterKnoten == 5:
if VectorMülleimer[57-2] != 0:
Kreuzung = 1
if VectorMülleimer[56-2] != 0:
Kreuzung = 2
if VectorMülleimer[57-2] == 0 and VectorMülleimer[56-2] == 0:
Kreuzung = randint (1,2)
if Kreuzung == 1:
aktuellerKnoten = 7
letzterKnoten = 4
Straße = 57
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
if Kreuzung == 2:
aktuellerKnoten = 3
letzterKnoten = 4
Straße = 56
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
elif aktuellerKnoten == 5:
aktuellerKnoten = 4
letzterKnoten = 5
Straße = 55
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
Vergleich Ausgangsmodell - Vereinfachtes Modell
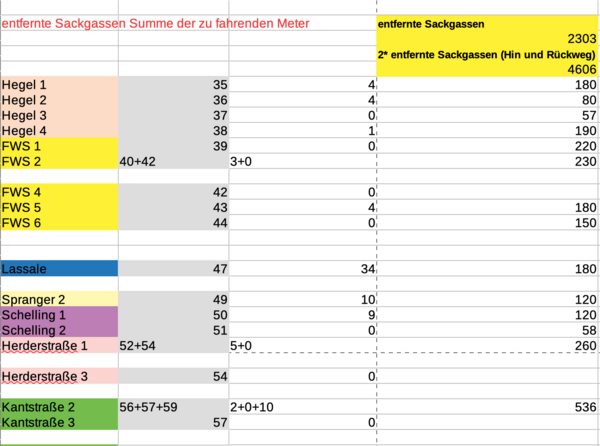
[Bearbeiten]Kürzeste Strecken:
- Kürzeste erhaltene Strecke vom Startknoten 2 aus: 12.353 Meter
- Kürzeste erhaltene Strecke vom Startknoten 3 aus: 11.892 Meter
- Kürzeste erhaltene Strecke Version Python 10.0: 10.920 Meter
Zeitenvergleich:
Startknoten 2:
Vereinfachtes Modell: Programm 3.0

Startknoten 3:
Vereinfachtes Modell: Programm 3.0

Anmerkung: Zeitangabe jeweils in Sekunden
Zyklus 4
[Bearbeiten]Um den optimalen Weg zu finden müssen Straßen, auch wenn sie keine Sackgassen sind, direkt wieder zurückgefahren werden. Dies haben wir per Hand herausgefunden, es in unserem 4. Zyklus mit berücksichtigt und haben dem Programm damit die Möglichkeit gegeben, eine Straße direkt doppelt zu fahren, auch wenn sie keine Sackgasse ist.
Ein Beispielknoten sieht dadurch wie folgt aus:
elif aktuellerKnoten == 49:
elif letzterKnoten == 50:
if VectorMülleimer[4-2] != 0:
Kreuzung = 1
if VectorMülleimer[50-2] != 0:
Kreuzung = 2
if VectorMülleimer[4-2] == 0 and VectorMülleimer[50-2] == 0:
Kreuzung = randint (1,3)
if Kreuzung == 1:
aktuellerKnoten = 48
letzterKnoten = 49
Straße = 4
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
if Kreuzung == 2:
aktuellerKnoten = 55
letzterKnoten = 49
Straße = 50
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
if Kreuzung == 3:
aktuellerKnoten = 50
letzterKnoten = 49
Straße = 5
Strecke = Strecke + VectorStrasse[Straße - 2]
geleerteMülleimer = geleerteMülleimer + VectorMülleimer[Straße - 2]
VectorMülleimer[Straße - 2] = 0
Python Version 10.0:
Das folgende Video stellt den Ablauf des gefundenen kürzesten Weges in unserem Straßennetz dar:
Zuordnung des Themas zu den Nachhaltigkeitszielen der Vereinten Nationen
[Bearbeiten]- SDG9 Industry, Innovation and Infrastructure
Der Müll soll möglichst effizient, kostengünstig und mit geringstem Aufwand abtransportiert werden und dadurch die Inrastruktur gefördert werden.
- SDG11 Sustainable Cities and Communities
Die Belastung der Städte und Siedlungen soll durch einen effektiven Abtransport des Mülls so gering wie möglich gehalten werden. Auch die Arbeitszeit der Angestellten ist so gering wie möglich zu halten, um das Unternehmen möglichst produktiv zu gestalten und durch die best errechneteste Strecke inovativ zu bleiben.
- SDG12 Responsible Consumption and Production
Die Stadtbildpflege soll durch effizientes Abfahren der Straßen möglichst Resourcen arm, den angesammelten Müll abtransportieren um die Nachhaltigkeit zu unterstützen.
- SDG15 Life on Land
Der Müll sollte sich nur die kurz möglichste Zeit auf den Straßen befinden, um weiterer Umweltverschmutzung vorzubeugen.
Fazit
[Bearbeiten]Nach Abschluss unseres Projektes können wir zusammenfassend sagen, dass wir unser Ziel erreicht und den kürzesten Weg für das Müllauto im ausgewählten Stadtbezirk Betzenberg gefunden haben. Die Länge aller Straßen beträgt 8366m und dem gegenüber steht eine Strecke von 10190m, die wir sowohl mit Libre Office Calc per Hand, als auch mit dem von uns programmierten System Python erhalten haben. Die Differenz erklärt sich zum einen dadurch, dass Sackgassen doppelt gefahren werden müssen, und zum anderen dadurch, dass bestimmte Straßen doppelt gefahren werden, um einen möglichst kurzen Gesamtweg zu erzielen.
Im Laufe des Modellierungsprozesses haben sich Schwächen des Programms Python gezeigt. Zum einen trat das Problem auf, dass das Programm beim automatischem Abfahren der Straßen nach der Leerung nicht mehr in diese Straße zurückfahren wollte, da die Mülleimer dort schon geleert wurden. Dies würde sich aber manchmal für das Erzielen eines kürzeren Gesamtweges lohnen. Da dies aber in der Realität nicht logisch ist, ist das Zurückfahren in geleerte Straßen eigentlich nicht sinnvoll. Eine weitere Lücke im Programm besteht darin, dass Einbahnstraßen, Fußgängerzonen und Verkehrsführung nicht beachtet werden. Außerdem steht der Arbeitsaufwand der Programmierung für die Straßenpläne in keinem Verhältnis zur Verbesserung des Weges und ist somit der Stadtbildpflege nicht zu empfehlen. Würde man das Vorgehen auf die ganze Stadt übertragen wäre der Arbeitsaufwand viel zu hoch. Um das Modell in Zukunft zu verbessern müssten zum einen die eben genannten Schwächen behoben werden, und zum anderen müsste ein Programm erstellt werden, welches unaufwändiger und für größere Bezirke zeiteffizienter zu erstellen ist.
Literatur
[Bearbeiten]- Krumke, S & Noltemaier, H (2012). Graphentheoretische Konzepte und Algortihmen. Wiesbaden: Vieweg + Teubner Verlag.