Das Bloch-Lorentz-Modell ermöglicht eine semiklassische Beschreibung der Besetzungszahlen und Intensität des Laserlichts. Es lässt sich durch einen Satz von drei gekoppelten Differentialgleichungen charakterisieren, die sich aus den Maxwellgleichungen herleiten lassen.

wobei folgende Größen verwendet werden:
 : Amplitude des elektrischen Feldes
: Amplitude des elektrischen Feldes : Amplitude der Polarisation des Laser-Mediums
: Amplitude der Polarisation des Laser-Mediums : Besetzungsinversion
: Besetzungsinversion : externe Pumprate
: externe Pumprate : Zerfallsrate des Laserfelds
: Zerfallsrate des Laserfelds : Zerfallskonstante der Inversion
: Zerfallskonstante der Inversion : Zerfallskonstante der Polarisation
: Zerfallskonstante der Polarisation : Verstimmung zwischen elektrischen Feld und Laser-Resonator
: Verstimmung zwischen elektrischen Feld und Laser-Resonator : Verstimmung zwischen elektrischen Feld und Resonanz des Laser-Mediums (zwei-Niveau-System)
: Verstimmung zwischen elektrischen Feld und Resonanz des Laser-Mediums (zwei-Niveau-System)
Dynamik der elektrischen Feldamplitude
[Bearbeiten]Die Gleichungen des Bloch-Lorenz-Modells aus einer Kombination der optischen Bloch-Gleichungen und den Maxwell-Gleichungen herleiten. Verbindet man makroskopisches Induktionsgesetz und Durchflutungsgesetz mit  und der Magnetisierung
und der Magnetisierung  erhält man die Wellengleichung mit Polarisation
erhält man die Wellengleichung mit Polarisation 

Mit dem Brechungsindex  des Mediums im Resonator. Wir wählen das elektrische Feld mit einfacher Mode
des Mediums im Resonator. Wir wählen das elektrische Feld mit einfacher Mode  wobei die Modenfunktion
wobei die Modenfunktion  den Resonator ohne Polarisation beschreibt und erfüllt die Helmholtz-Gleichung
den Resonator ohne Polarisation beschreibt und erfüllt die Helmholtz-Gleichung

Die Frequenz  ist die Eigenfrequenz des Resonators. Wählt man die selbe Zerlegung für die Polarisation wie für das elektrische Feld lässt sich die Ortsabhängigkeit der Felder eliminieren
ist die Eigenfrequenz des Resonators. Wählt man die selbe Zerlegung für die Polarisation wie für das elektrische Feld lässt sich die Ortsabhängigkeit der Felder eliminieren

Eine weitere Zerlegung trennt die zeitabhängige Amplitude  von der Oszillation des Laserfeldes bei
von der Oszillation des Laserfeldes bei  . Nun wird die Feldamplitude im Resonator durch die Auskopplung und Absorbtion gedämpft und
. Nun wird die Feldamplitude im Resonator durch die Auskopplung und Absorbtion gedämpft und 

Auf der linken Seite können die Terme  und
und  unter der Annahme, dass die Amplitude sich langsam im Vergleich zur Laserfeldoszillation verändert (slowly varying envelope approximation). Es verbleibt
unter der Annahme, dass die Amplitude sich langsam im Vergleich zur Laserfeldoszillation verändert (slowly varying envelope approximation). Es verbleibt

wobei für die Polarisation ebenfalls approximiert wurde, dass  . Die obige Formel für die Amplitude des elektrischen Feldes wird mit
. Die obige Formel für die Amplitude des elektrischen Feldes wird mit  bis auf den Faktor vor
bis auf den Faktor vor  erhalten.
erhalten.

Die Polarisationsdichte des Mediums, ohne Interaktion mit den eigenen Dipolmomenten, kann mit der Anzahldichte  und dem gemittelten elektrischen Dipolmomenten
und dem gemittelten elektrischen Dipolmomenten  durch
durch  ausgedrückt werden. Unter der Annahme, dass die Zweiniveausysteme im Resonator homogen verteilt sind, lässt sich eine ortsunabhängige Zweiniveaudichte
ausgedrückt werden. Unter der Annahme, dass die Zweiniveausysteme im Resonator homogen verteilt sind, lässt sich eine ortsunabhängige Zweiniveaudichte  verwenden. Die Polarisationsdichte wird durch das elektrische Feld als positiv und negativ rotierende Größe und kann in der rotating frame approximation (Drehwellennäherung) als
verwenden. Die Polarisationsdichte wird durch das elektrische Feld als positiv und negativ rotierende Größe und kann in der rotating frame approximation (Drehwellennäherung) als

gegeben. Hier ist  das Dipolmatrixelement,
das Dipolmatrixelement,  das Dichtematrixelement des Zweiniveau-Übergangs und
das Dichtematrixelement des Zweiniveau-Übergangs und  die Richtung des elektrischen Feldes. Für die Dynamik der Amplitude der Oszillation ist es ausreichend
die Richtung des elektrischen Feldes. Für die Dynamik der Amplitude der Oszillation ist es ausreichend  zu betrachten, da
zu betrachten, da  gilt. Für die Zeitableitung
gilt. Für die Zeitableitung  werden die Bloch-Gleichungen im rotating frame approximation verwendet.
werden die Bloch-Gleichungen im rotating frame approximation verwendet.

Mit der Verstimmung zwischen Laserfeld und Atomübergang  und der Rabifrequenz
und der Rabifrequenz  . Die diagonalen Matrixelemente
. Die diagonalen Matrixelemente  und
und  als Differenz geben die Inversion des Mediums
als Differenz geben die Inversion des Mediums  an. Damit wird die Form der obigen Gleichung für die Amplitude der Polarisation erhalten:
an. Damit wird die Form der obigen Gleichung für die Amplitude der Polarisation erhalten:

Hier ein erstes Bild: dazu erst einloggen und über commons.wikimedia.org die Grafik hochladen. Der Dateiname (hier ganz lakonisch Beispiel_01.png) kann dann mit Datei:Beispiel_01.png|420px|rahmenlos|links verlinkt werden.

Es wird der Fall konstanter Inversion angenommen. Das Gleichungssystem reduziert sich auf zwei Gleichungen.

Das System besitzt einen Fixpunkt bei  und ist bereits linear, da die Inversion
und ist bereits linear, da die Inversion  eine Konstante ist.
Mit Hilfe eines Phasenportraits wird die Stabilität des Fixpunktes überprüft, welcher in diesem Fall gewählter Parameter stabil ist. (Für die Portraits sind nur reelle Werte für F und P eingesetzt worden.)
eine Konstante ist.
Mit Hilfe eines Phasenportraits wird die Stabilität des Fixpunktes überprüft, welcher in diesem Fall gewählter Parameter stabil ist. (Für die Portraits sind nur reelle Werte für F und P eingesetzt worden.)
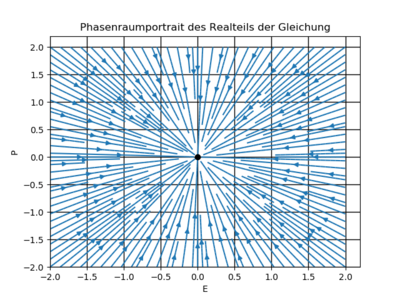
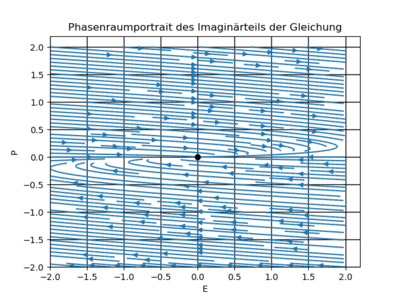
Die Stabilität des Fixpunkts ergibt sich aus den Eigenwerten  der
der  Matrix
Matrix
![{\displaystyle {\begin{pmatrix}-(\kappa +{\rm {i}}\delta _{c})&{\rm {i}}\kappa \\-{\rm {i}}\gamma _{I}\Delta n&-(\gamma _{P}+{\rm {i}}\delta )\end{pmatrix}}\rightarrow \mu _{1,2}=-{\tfrac {1}{2}}(\kappa +{\rm {i}}\delta _{c}+\gamma _{P}+{\rm {i}}\delta )\pm {\tfrac {1}{2}}{\Big [}(\kappa +{\rm {i}}\delta _{c}-\gamma _{P}-{\rm {i}}\delta )^{2}+4\kappa \gamma _{I}\Delta n{\Big ]}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aee457dc08a6092a5893db9689763f27b1a71f4)
Wenn die Wurzel (im Realteil) “groß genug” wird, wird  einen positiven Realteil haben: instabiler Fixpunkt. Dazu wählt man am besten
einen positiven Realteil haben: instabiler Fixpunkt. Dazu wählt man am besten  , weil das Quadrat unter der Wurzel negativ beiträgt. Für diesen Fall tritt Instabilität auf, wenn
, weil das Quadrat unter der Wurzel negativ beiträgt. Für diesen Fall tritt Instabilität auf, wenn

Wenn im Resonator die Verlustrate  stark anwächst, kann die Amplitude des Laserfelds durch eine stationäre Gleichung beschrieben werden:
stark anwächst, kann die Amplitude des Laserfelds durch eine stationäre Gleichung beschrieben werden:

So vereinfachen sich die oben genannten Differentialgleichungen zu

Diese Näherung erweist sich nur für gewisse Werte  als sinnvoll. Die folgenden Abbildungen zeigen jeweils auf der rechten Seite die Bad-Cavity-Approximation für verschiedene Verlustraten.
als sinnvoll. Die folgenden Abbildungen zeigen jeweils auf der rechten Seite die Bad-Cavity-Approximation für verschiedene Verlustraten.









Vergleich zum Lorenz-System und Übergang ins Chaos
[Bearbeiten]In diesem Abschnitt werden die Gleichungen des Bloch-Lorenz-Modells mit dem Gleichungssystem des Lorenz-Attraktors verglichen. Die Lorenzgleichungen sind in ihrer dimensionsloser Darstellung ein System aus drei gekoppelten, nichtlinearen Differentialgleichungen.

Die Parameter  sind Konstanten, die das Verhalten des Systems bestimmen und bei geeigneter Wahl einen seltsamen Attraktor entstehen lassen.
sind Konstanten, die das Verhalten des Systems bestimmen und bei geeigneter Wahl einen seltsamen Attraktor entstehen lassen.
- Ein direkter Vergleich zwischen dem Lorenz-System und dem hier gegebenen Bloch-Lorenz-Modell ist nicht ohne weiteres möglich. Das Lorenz-System besitzt drei reelle Variablen und drei reelle Parameter, während das Bloch-Lorenz-Modell aus einer reellen Größe
 , zwei komplexen Größen
, zwei komplexen Größen  und sechs reellen Parametern
und sechs reellen Parametern  besteht. Daher wird in einem ersten Schritt das Bloch-Lorenz-Modell in fünf reelle Gleichungen umgeformt.
besteht. Daher wird in einem ersten Schritt das Bloch-Lorenz-Modell in fünf reelle Gleichungen umgeformt.
- Dabei wird mit der folgende Notation die Gleichung skaliert.

Mit den skalierten Größen, der Verstimmung des Resonators zum Laserfeld  , der Verstimmung der Medium-Resonanz zum Laserfeld
, der Verstimmung der Medium-Resonanz zum Laserfeld  und skalierter Pumprate
und skalierter Pumprate  .
.
- Anschließend werden die Variablen in komplexer Schreibweise eingesetzt
 ;
;  und die Gleichungen können über die fünf reellen Variablen dargestellt werden.
und die Gleichungen können über die fünf reellen Variablen dargestellt werden.

Nun wird unter der Annahme einer reellen Amplitude des elektrischen Feldes  die zweite Bedingung algebraisch mit
die zweite Bedingung algebraisch mit  . Ohne Verstimmungen
. Ohne Verstimmungen  wird
wird  über die dritte Gleichung von ihrem Anfangswert exponentiell Abklingen und durch fehlende Kopplung mit den anderen Gleichungen lässt sich
über die dritte Gleichung von ihrem Anfangswert exponentiell Abklingen und durch fehlende Kopplung mit den anderen Gleichungen lässt sich  motivieren.
motivieren.
- Es verbleiben drei Gleichungen

Eine Reduktion der Parameter ist noch über das Einführen einer neuen Zeit  möglich. Es verbleiben
möglich. Es verbleiben  und
und 
- Further soon
























































![{\displaystyle {\begin{pmatrix}-(\kappa +{\rm {i}}\delta _{c})&{\rm {i}}\kappa \\-{\rm {i}}\gamma _{I}\Delta n&-(\gamma _{P}+{\rm {i}}\delta )\end{pmatrix}}\rightarrow \mu _{1,2}=-{\tfrac {1}{2}}(\kappa +{\rm {i}}\delta _{c}+\gamma _{P}+{\rm {i}}\delta )\pm {\tfrac {1}{2}}{\Big [}(\kappa +{\rm {i}}\delta _{c}-\gamma _{P}-{\rm {i}}\delta )^{2}+4\kappa \gamma _{I}\Delta n{\Big ]}^{1/2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4aee457dc08a6092a5893db9689763f27b1a71f4)


































