Infinitesimalrechnung I

Wir entschuldigen uns für die deutschsprachigen Syntaxfehler. Siehe Diskussion. Bitte übersetzen Sie diese Seite besser Deutsch. Entspannen Sie sich. Bearbeiten Sie einen Section pro Tag.

Infinitesimalrechnung I ist ein Mathe Kurs in w:Grundständiges Studium weltweit. Es deckt in der Regel eine bekannte Teilmenge der Themen von w:Infinitesimalrechnung, die ein Zweig der Mathematik ist, die mit der Feststellung befasst und Eigenschaften von w: Differentialrechnung#Ableitung als eine Funktion und w: Integralrechnung andere Funktionen. Viele Studenten in den w: MINT-Fächer weltweit Felder müssen ausgefüllt werden entweder auf Kredit über Amerikaa en:w:AP Calculus (oder das Äquivalent in der High School) erhalten oder Infinitesimalrechnung I. Viele Institution nehmen auch Kurse genannt Infinitesimalrechnung II und Infinitesimalrechnung III. Einige Schüler finden Infinitesimalrechnung I entmutigend sein, wegen seiner abstrakten Natur aufgrund der Strenge und Förmlichkeit, die erweitert und verallgemeinert das Thema in der 200 Jahre, nachdem es elegant durch Newton und Leibniz definiert wurde.

Artikel Ziele: dem Leser Geben Sie eine w: Bootstrapping sd Schnellstart-Anleitung für Infinitesimalrechnung I für den Anfänger oder für diejenigen mit Infinitesimalrechnung I. kämpfen Es ist beabsichtigt, das zu geben, Leser eine hervorragende schnell in der Infinitesimalrechnung Vorsprung.

Dieser Artikel opfert ein wenig Strenge und Allgemeinheit aus Gründen der viel eschwindigkeit Lernen. Es umfasst Konzepte und Funktionen, die sein können sichtbar. Infinitesimalrechnung Mathematik Notation und Nomenklatur sind im Stil von eingeführt w: Just-in-time-Produktion für die richtige w: Pädagogik. In diesem Artikel werden nur Kurven betrachten, die eine sind w: Stetigkeit w: Funktionsgraph $f(x)$ e ohne w: Unstetigkeitsstelle . w: Kartesisches Koordinatensystem und Punkte auf den Kurven sind dargestellt, als $(x,y)$ Koordinaten Kurven werden im Allgemeinen diskutiert.

Der Umfang der Infinitesimalrechnung I Themen wie Abschnitten dargestellt sind:

• Der w: Potenzregel (für nur ganzzahlige Potenzen) nur eine geringe Menge an w:Algebra, w:Geometrie und w:Grenzwert (Funktion) verwendet wird.
• Der Infinitesimalrechnung Grundlagen der beiden w: trigonometrische Funktionen w: Sinus und w: Kosinus
• Der Infinitesimalrechnung Grundlagen der w: Logarithmus#Natürlicher Logarithmus und w: Exponentialfunktion
• Einige Regeln der Differenzierung und Integration

Funktionen, Kurven und die Steigung-Funktionswerte-Flächeninhalt tripel

Die einfache Parabel

Betrachten Sie die Kurve $y(x)=x^{2}$, das dieser Artikel bezieht sich auf die "einfachen Parabel". Für jeden gegebenen positiven Funktionswerte von $x$ genannt $x_{1}$, geht diese Kurve durch den Punkt $(x_{1},x_{1}^{2})$. Wir nennen diesen Punkt $X_{1}$. Bei $X_{1}$ der Steigung-Funktionswerte-Flächeninhalt W: Tripel:

• Die w: Steigung an diesem Punkt "dieser Kurve '(die momentane Steigung oder Änderungsrate). Diese Steigung ist das "Derivat" bezeichnet. Berechnung der Ableitung wird als "Differenzierung" genannt.
• Die Funktionswerte des w: numerische Funktion (der Funktionswerte von $y$) ist $x_{1}^{2}$.
• Die w: Flächeninhalt unter der Kurve in $x_{1}$. Das ist das Gebiet begrenzt durch:
  • Die Kurve selbst von $(0,0)$ zu $X_{1}$
  • Die vertikale Liniensegment von $X_{1}$ zu $(x_{1},0)$
  • Das horizontale Liniensegment $(x_{1},0)$ zu $(0,0)$. Dieser Flächeninhalt ist das "Integral" genannt. Berechnen des Integrals als "Integration" bekannt.

Nicht undefinierten Werte und andere Sonderfälle

Bei der Berechnung der Steigung einer geraden Linie, ist die Formel

${\text{steigung}}={\frac {\Delta y}{\Delta x}}$

aber wir können nicht direkt, dass die Formel für die momentane Steigung einer Kurve verwenden, da ${\frac {0}{0}}$ ist ein undefinierten Wert und einem Ausdruck wie Null-geteilt-für- Null ist ein w: Unbestimmter Ausdruck (Mathematik). Wir werden dieses Problem lösen, indem sie Grenzen nutzen.

In Potenzierung, ist ein weiterer nicht definierten Wert $0^{0}$. Dies ist zum Teil, weil dieser zwei Grenze s, die zwei verschiedene Werte nähern:

$\lim _{x\to 0}0^{x}=0$

$\lim _{x\to 0}x^{0}=1$

Diese beiden nähern nicht den gleichen Wert. Wir verwenden eine positive Basis wie $2^{x}$. Wenn wir $(-2)^{x}$ betrachten, finden wir, dass in $x={\frac {1}{2}}$ (oder irgendeine andere w: rationale Zahl das kann ausgedrückt als eine ungerade ganze Zahl durch eine gerade Zahl) aufgeteilt werden, beinhaltet der Wert ${\sqrt {-2}}$ und damit zu den w: imaginäre Einheit, so dass wir solche Kurven in diesem Artikel zu vermeiden. Wenn Sie ein Diagramm wie $y={\sqrt {|x|}}$ oder andere potenzen zwischen Null und Eins, dann gibt es eine w: Spitze (Singularitätentheorie) in $(0,0)$ und die Steigung an diesem Punkt undefiniert.

Potenzregel

Die Leistungsregel ist in der Regel der erste in Infinitesimalrechnung I abgedeckt Regel. In diesem Abschnitt wird zunächst ein nicht Infinitesimalrechnung Ansatz, um es nehmen und dann in der nächsten großen Abschnitt diskutieren ihre Auswirkungen für Infinitesimalrechnung.

Ein Muster in ganzzahlige Potenzen von "x"

Der Begriff "Kurve" schließt gerade Linien. Vielleicht ist die einfachste Kurve ist die Gerade $y=0$:

Steigung	Funktionswerte	Flächeninhalt
0	0	0

Die nächste Kurve ist $y=x^{0}=1$:

Steigung	Funktionswerte	Flächeninhalt
0	1	$x$

Mit "$x$", was wir meinen ist, dass die Fläche unter der Kurve ist die w: Rechteck das ist 1 durch $x_{1}$, das wir zum Ausdruck bringen einfach als Raum der Größe math -start x</math>.

Die nächste Kurve ist $y=x^{1}=x$.

Steigung	Funktionswerte	Flächeninhalt
1	$x$	${\frac {1}{2}}x^{2}$

Das Gebiet ist eine Hälfte eines w: Quadrat mit der Seitenlänge von $x_{1}$. Der Platz ist in zwei Hälften durch die Kurve geschnitten, die eine Diagonale ist auf den Platz. In dieser dreifachen entsteht ein Muster, dass die {potenz $x$ um eins erhöht, wie die Begriffe von links nach rechts fortschreiten. Das Muster ist weniger offensichtlich in den früheren verdreifacht.

Betrachten wir noch einmal die einfache Parabel, die Kurve $y=x^{2}$:

Steigung	Funktionswerte	Flächeninhalt
$2x$	$x^{2}$	${\frac {1}{3}}x^{3}$

Das Muster im Potenzen von $x$ ist noch deutlicher, und es ist ein Muster in den Koeffizienten (2,1, ${\frac {1}{3}}$).

Zwei Beweise für die einfache Parabel

Folgendes ist ein Beweis für die Steigung und die Fläche der einfachen Parabel Während Infinitesimalrechnung Beweise sind in der Regel nicht in Infinitesimalrechnung I Untersuchungen erwartet.

Ableitung der einfachen Parabel

Eine Sekante eine Tangente als $\Delta x$ immer auf Null geht

Um die Steigung der einfachen Parabel berechnen, betrachten wir zwei Punkte auf der Parabel für einige positive Funktionswerte von $x_{1}$ und positive $h$ die beiden Punkte:

$X_{1}$ in $(x_{1},x_{1}^{2})$

$X_{2}$ in $(x_{1}+h(x_{1}+h)^{2})$

Zeichnen Sie eine Linie (entweder das Liniensegment $X_{1}X_{2}$, das ist ein Sehne oder die entsprechenden w: Sekante). Nun verringern $h$, bis es gegen Null geht. Das Akkord haben eine Steigung, die die Steigung der Kurve an der $X_{1}$ nähert. Bewerten Sie die Steigung der Linie und nehmen Sie die Grenze (die Steigung der w: Tangente):

${\begin{aligned}{\text{Neigung}}&={\frac {\Delta y}{\Delta x}}\\[8pt]&={\frac {(x_{1}+h)^{2}-x_{1}^{2}}{(x_{1}+h)-x_{1}}}\\[8pt]&={\frac {(x_{1}^{2}+2hx_{1}+h^{2})-x_{1}^{2}}{h}}\end{aligned}}$

(Beachten Sie, dass alle Begriffe verschwinden in den nächsten Schritten mit Ausnahme des zweiten von der linken Begriff $2hx_{1}$)

$={\frac {2hx_{1}+h^{2}}{h}}$

$=2x_{1}+h$

$\lim _{h\to 0}(2x_{1}+h)=2x_{1}$

Hinweis für den Begriff $(x+h)^{2}$, dehnt es sich auf $(x^{2}+2hx+h^{2})$, mit numerischen Koeffizienten von 1,2,1. Auf die Leistung (der Potenz) 3, ist das Muster 1,3,3,1. Der Funktionswerte $2x$ entspricht der Begriff, der zwei von in Reihe zweiter von-the-links ist w: Pascalsches Dreieck, mit all den Begriff (e) auf der rechten Seite mit einer Leistung $h$, die verschwinden, wie $h$ auf Null geht. Die Kurve $y=x^{3}$ führt 3 des Dreiecks zu rudern und die Steigung ist $3x^{2}$. Wir haben jetzt die Basis für die Suche nach der Steigung von $y=x^{n}$ für jede ganze Zahl $n$.

Integral der einfachen Parabel

Dieses Diagramm, das eine Annäherung unter einer Kurve in einen Flächeninhalt zeigt, geht von blau nach rot wie n $\infty$.

Um den Flächeninhalt der einfachen Parabel berechnen, stellen eine endliche Menge des Flächeninhalt von 0 bis Dividieren $x_{1}$ Konstruktion $n$ vertikal gleicher Breite Rechtecke. Berechnen Sie die Summe der Fläche dieser Rechtecke und nehmen Sie die Grenze als $n$ gegen unendlich geht:

${\begin{aligned}{\text{Flächeninhalt}}&=\lim _{n\to \infty }\sum _{i=1}^{n}{\text{Rechteck Flächeninhalt }}_{i}\\[8pt]&=\lim _{n\to \infty }\sum _{i=1}^{n}({\text{Höhe }}_{i}){\text{Breite}}\\[8pt]&=\lim _{n\to \infty }\sum _{i=1}^{n}f(x_{i})\,\Delta _{x}\\[8pt]&=\lim _{n\to \infty }\sum _{i=1}^{n}\left(\left({\frac {x_{1}i}{n}}\right)^{2}{\frac {x_{1}}{n}}\right)\\[8pt]&=\lim _{n\to \infty }{\frac {x_{1}^{3}}{n^{3}}}\sum _{i=1}^{n}i^{2}\end{aligned}}$

(Beachten Sie die Summe der Folge von Plätzen, für die wir verwenden, um die entsprechenden nicht-faktorisierter Leistungssumme Formel)

${\begin{aligned}&=\lim _{n\to \infty }{\frac {x_{1}^{3}}{n^{3}}}{\frac {1}{6}}(2n^{3}+3n^{2}+n)\end{aligned}}$

(Beachten Sie, dass alle Begriffe mit Ausnahme der am weitesten links mit der höchsten Potenzen $2n^{3}$ verschwinden)

${\begin{aligned}\quad &={\frac {2x_{1}^{3}}{6}}\\[8pt]&={\frac {1}{3}}x_{1}^{3}\end{aligned}}$

Für die Kurve $y=x^{3}$, das nicht-faktorisierter Leistungssumme der Würfel ist ${\frac {1}{4}}(n^{4}+2n^{3}+n^{2})$ . Siehe auch Sums von Befugnissen. Alle Bedingungen mit Ausnahme der am weitesten links stehende Begriff mit dem höchsten Potenzen verschwinden und die Ergebnisse sind:

Steigung	Funktionswerte	Flächeninhalt
$3x^{2}$	$x^{3}$	${\frac {1}{4}}x^{4}$

Und so weiter für höhere Leistungen. So können wir den Flächeninhalt für die $y=x^{n}$ für jede ganze Zahl $n$ außer für $berechnenn=(-1)$, das mit dem natürlichen Logarithmus in Beziehung steht. Der Vollständigkeit halber sind hier die nicht-faktorisierter Leistungssummen für Potenz 1 bis 5:

$\sum _{i=1}^{n}i^{1}={\frac {1}{2}}(n^{2}+n)$

$\sum _{i=1}^{n}i^{2}={\frac {1}{6}}(2n^{3}+3n^{2}+n)$

$\sum _{i=1}^{n}i^{3}={\frac {1}{4}}(n^{4}+2n^{3}+n^{2})$

$\sum _{i=1}^{n}i^{4}={\frac {1}{30}}(6n^{5}+15n^{4}+10n^{3}-n)$

$\sum _{i=1}^{n}i^{5}={\frac {1}{12}}(2n^{6}+6n^{5}+5N^{4}-n^{2})$

Leistungsregel für die Differenzierung und Integration

Für ganzzahlige $n$ und der Kurve $y=x^{n}$, die Macht Regel (n) Zustand:

Derivative von fuction	Funktion	Integral von fuction
$nx^{n-1}$	$x^{n}$	${\frac {1}{n+1}}x^{n+1}$

Diese Formeln sind wahr für jeden ganzzahligen Funktionswerte von $n$ außer für $n=(-1)$ für das Integral. Das ist die Kurve $y={\frac {1}{x}}$, das ein Sonderfall ist dem natürlichen Logarithmus verwandt. Diese Formeln können auf einen beliebigen Funktionswerte von $n$ (jede reelle Zahl einschließlich nicht-ganzzahlige Funktionswerte) verallgemeinert werden, aber dieser Artikel vermeidet für dasselbe Thema.

Netz Regel Auswirkungen auf Infinitesimalrechnung

Wir wissen bereits, dass die Steigung der Ableitung des Value-Kurve ist und die Gegend ist das Integral der Kurve. Durch die Macht der Regel untersuchen, sehen wir, dass Ableitung und Integral sind (nahezu perfekt) w: Umkehrfunktion voneinander. Dies gilt nicht nur für die Potenzen von x, aber für irgendein w: Stetigkeit . Dies ist einer der großen Einsichten von Newton und Leibniz. Die Ableitung des Integral der Kurve ist nur die Kurve wieder (und umgekehrt). Dies impliziert die überraschenden Ergebnisse, dass der Funktionswerte der Integral der Steigung ist, und der Funktionswerte ist die Ableitung des Flächeninhalts. Das Verhältnis zwischen Fläche und Funktionswerte (und dass zwischen Funktionswerte und Steigung) ist bidirektional. Da zwei benachbarten Spalten in einem der Tische, ist das Element auf der linken Seite das Derivat des Elements auf der rechten Seite und der Position auf der rechten Seite ist das Integral der Artikel auf der linken Seite. Hinzu kommt, dass, ist das Element zwei Spalten auf der linken Seite der zweite Ableitung. Weitere Spalten können für den Nachweis noch höherer Ordnung Ableitungen und Integrale zu den Tabellen hinzugefügt werden.

Um diese bidirektionale Beziehung betonen, betrachten die beiden Funktionen $y=2x$ und $y=x^{2}$. Der Flächeninhalt der ersten Kurve ist $2({\frac {1}{2}}x^{2})$ oder nur $x^{2}$. Die Steigung dieser letzteren Kurve ist $2x$ beginnen und wir kehren zu unserer ursprünglichen Formel, wie wir die Ableitung des Integral (oder das Integral des Derivats) nehmen.

Die Ableitung und Integral sind w: lineare Funktion s. So ist die Steigung von $(f(x)+g(x))$ entspricht der Steigung der $f(x)$ sowie die Steigung der $g(x)$. Das gleiche gilt für Integral.

Physikalische Modelle von derivativen und Integral

Derivate für 1-, 2- und 3-dimensionale Objekte

Betrachten Sie die Funktionswerte der $x$ als die Zeit darstellt $t$. Betrachten Sie $y$ als zeitlich veränderliche Funktion $y=f(t)$ und das Differential untersuchen. $dt$ ist ein w: infinitesimal (ähnlich der Grenze als $dt$ auf Null geht).

Für den eindimensionalen Fall ist y Länge von stetig wachsenden Faden $L$ mit einem Ende an festgelegt $(0)$ und am anderen Ende wächst, also $L(t)=t$ dh Länge linear mit der Zeit wächst, wie vielleicht eine dünne Eiszapfen, so ist das Wachstum:

$dL=dt$

${\frac {d}{dt}}L=1$

${\frac {d}{dt}}t=1$

Diese letzte Zeile ist eine der üblichen mathematischen Schreibweisen für die Ableitung.

Für den zweidimensionalen Fall, stellen wir eine quadratische dünne Schicht eines Eis, die auf dem Ursprung $(0,0)$ wächst entlang der beiden gegenüberliegenden Seiten der x-Achse und der y-Achse stabil ist, somit ist der Flächeninhalt $A(t)=t^{2}$. Das Wachstum über ein wenig Zeit ist die sume von:

• Das Wachstum der beiden Wachstums Seiten des Platzes
• Das kleine Quadrat des Wachstums an der Ecke gegenüber $(0,0)$:

$dA=(2t)\,dt+(dt)^{2}$

\frac ${d}{dt}A=2t+dt$

aber $dt$ ein unendlich ist, so dass alle, aber die am weitesten links stehende Term verschwindet:

${\frac {d}{dt}}A=2t$

${\frac {d}{dt}}t^{2}=2t$

Die Produktregel (die später behandelt werden), kann die gleiche Gleichung schreiben als:

$dA=(t\,t)dt$

$dA=(t)dt+(dt)t$

Für den dreidimensionalen Fall betrachten wir eine wachsende Eiswürfel mit einer Ecke in festgelegt $(0,0,0)$ mit Volumen $V(t)=t^{3}$. Das Wachstum des Volumens über einen kurzen Zeitraum $dV(t)$ ist die Summe von:

• Das Wachstum entlang der drei Seiten des Würfels gegenüber den drei Ebenen des Koordinatensystems
• Das Wachstum an den Rändern gegenüber den drei Achsen des Koordinatensystems
• Der kleine Würfel gegenüber dem $(0,0,0)$ Ecke:

$dV=(3t^{2})dt+(3t)(dt)^{2}+(dt)^{3}$

${\frac {d}{dt}}V=3t^{2}+(3T)\,dt+(dt)^{2}$

und da $dt$ ist ein unendlich so alle, aber die am weitesten links stehende Term verschwindet:

${\frac {d}{dt}}V=3t^{2}$

${\frac {d}{dt}}t^{3}=3t^{2}$

In allen drei Fällen ist die Ableitung (Wachstumsrate) des dreidimensionalen Objektmenge die gleiche wie für die Steigungen der Kurven der Befugnisse der $x$ und die gleiche wie das, was die Macht der Regel findet.

Physik

Betrachten Sie in w: Physik ein Ball geworfen horizontal weg von einem hohen Gebäude. Die Horizontalgeschwindigkeit konstant ist und die horizontal zurückgelegten Wegstrecke ist horizontal Geschwindigkeit mal Zeit. In der Vertikalen haben wir die Beschleunigung Geschwindigkeitsstrecken tripel wo vertikale Beschleunigung konstant ist. Bearbeitung

• Die Spitze des Gebäudes als unsere "Null Höhe" w: Bezugssystem
• Die Abwärtsrichtung als die positive Richtung
• Der w: Gravitationskonstante als $a$ (die Beschleunigung)

dann wird der Ball den Weg der einfachen Parabel folgt um einen Faktor skaliert, um $a$. In der vertikalen $v(t)=an$ und der dreifache ist:

Beschleunigung	Geschwindigkeit	Entfernung
$a$	$at$	${\frac {1}{2}}t^{2}$

So haben wir die bekannte Formel $s(t)={\frac {1}{2}}auf^{2}$. Die Formel für die w: kinetische Energie, $E={\frac {1}{2}}mv^{2}$ hat die gleiche Form aus ähnlichen Gründen.

Ein Geld tripel

Angenommen, Sie haben ohne Mietvertrag eine Wohnung mieten und die Miete geht ein wenig jeden Monat auf. Die Miete ist eine Rate: US-Dollar pro Monat. Eine graphische Darstellung der Miete jeden Monat, da Sie bewegt in und einer glatten Kurve durch die Datenpunkte würde die Miete als eine Funktion der Zeit darzustellen. Die dreifache ist:

Steigung	Funktionswerte	Flächeninhalt
Rate der monatlichen Anstieg der Miete	Mieten	Total Geld bezahlt

Eine richtige Finanzplaner können diese drei Funktionswerte verwenden, um besser fundierte Entscheidungen und Prognosen. Viele andere praktische Analogien wie Kraftstoff aus einem Kraftstofftank (oder einem Wasserbehälter, etc.) gefüllt und verbraucht sind möglich.

Weiterentwicklung der Definition des Integrals

Ein Integral einer Funktion kann als signierte Fläche der Region durch ihren Graphen begrenzt dargestellt werden

Für andere Funktionen mit negativen Werten (wie $sin(x)$ und $cos(x))$, der Flächeninhalt für negative Funktionswerte von $y$ subtrahieren von der positiven kumulierten Flächeninhalt zunächst als $x$ von Null angesammelt.

Die w:Stammfunktions der Kurven, die weit so passieren $(0,0)$ und haben somit eine w: Integrationskonstante berücksichtigt wurden pf Null und somit haben wir ignoriert sie. Wir definieren nun das Integral als antiderivative plus der Konstante der Integration. Die Integrationskonstante ist das Negativ der antiderivatve in $x=0$. Definiert als solche, berechnet das Integral geht immer durch $(0,0)$.

Betrachten Sie Skimming w: Fundamentalsatz der Analysis für einen Hauch von einem sehr viel strenger und allgemeine Behandlung dieser Konzepte.

Sinus und Kosinus

Sinus und Kosinus

Sinus und Kosinus sind ein Paar von trigonometrischen Funktionen werden wir die "trig-Paar" nennen. In Infinitesimalrechnung, haben die trig Paar eine Beziehung miteinander. Bei $(0,0)$, die Steigung der $\sin(x)$ Funktion gleich 1. Als $x$ erhöht sich auf ${\frac {\pi }{2}}$ kann der Leser spüren, dass die Steigung der $\sin(x)$ ist $\cos(x)$. Die Steigung der $\cos(x)$ ist $-\sin(x)$. Das trig Paar haben einen vier Iterationszyklus Zeitraum für höhere Ordnungen von Derivaten:

Vierte Ableitung	Dritte Ableitung	Zweite Ableitung	Steigung	Funktionswerte
$\sin(x)$	$-\cos(x)$	$-\sin(x)$	$\cos(x)$	$\sin(x)$

Die vierte Ableitung von $\sin(x)$ ist nur $\sin(x)$ wieder und der Zyklus wiederholt sich. Beachten Sie, dass die physikalische Bedeutung der Tatsache, dass die zweite Ableitung der $\sin(x)$ ist $-\sin(x)$. Dies ist für einfache harmonische Bewegung. Für ein schweres Gewicht an einer Feder hängt, ist die Verschiebung aus dem Ruhezustand proportional zu der w: Rückstellkraft (die in der Beschleunigung führt), aber im negativen (gegenüber) Richtung. Für eine Anwendung solcher in analoger Elektronik, siehe w: Schwingkreis.

Das Integral der $\cos(x)$ ist $\sin(x)$, aber das Integral von $\sin(x)$ beinhaltet eine Konstante ungleich Null der Integration. Das Integral ist $1-\cos(x)$. Es besteht aus:

• Die antiderivative von $\sin(x)$, das $-\cos(x)$ ist
• Die antiderivative, die $-\cos(x)$, ausgewertet bei $x=0$ ist, die (-1) ist. Somit ist die Integrationskonstante ist - (- 1) oder einfach 1.

Die Kurve $1-\cos(x)$ beginnt bei $(0,0)$ und bildet dann eine Reihe von Hügeln, die von der x-Achse steigen, Spitzen bei $y=2$ und dann fallen wieder auf Null als $x$ zunimmt. Wiederholte Integration ergibt:

Funktionswerte	Flächeninhalt	Doppelintegral	Dreibettzimmer Integral	Quadruple Integral
$\sin(x)$	$1-\cos(x)$	$x-\sin(x)$	$1+{\frac {1}{2}}x^{2}+\cos(x)$	$x+{\frac {1}{6}}x^{3}+\sin(x)$

Während die trig Paar Komponente dieser Formeln tut Zyklus um die Begriffe, die Befugnisse der $x$ sind akkumulieren.

Auch Weiterentwicklung der Definition des Integrals

Das bestimmte Integral findet die Fläche unter einer Kurve mit den beiden begrenzenden von $x$ nicht unbedingt Null

Wir definierten zunächst das Integral als die Fläche unter der Kurve von $(0,0)$ zu $(x,f(x))$. Wir erweitern die Definition der Fläche unter der Kurve von $x_{1}$ zu $x_{2}$ (Unter der Annahme $x_{1}<x_{2}$ der Einfachheit halber) Als das Gebiet begrenzt durch:

• Die Kurve von $(x_{1},f(x_{1}))$ zu $(x_{2},f(x_{2}))$
• Die vertikale Liniensegment von $(x_{2},f(x_{2}))$ zu $(x_{2},0)$
• Das horizontale Liniensegment $(x_{2},0)$ zu $(x_{1},0)$
• Die vertikale Linie von $(x_{1},0)$ zu $(x_{1},f(x_{1}))$.

Die w:bestimmte Integral ist die Fläche unter der Kurve von $(x_{1},f(x_{1}))$ zu $(x_{2},f(x_{2}))$. Um zu bewerten es, die Berechnung der Fläche unter $(0,0)$ zu $(x_{2},f(x_{2}))$ und ziehen Sie die Fläche unter $(0,0)$ In den $(x_{1},f(x_{1}))$. In Standard Infinitesimalrechnung Notation ist das bestimmte Integral:

$\int _{x_{1}}^{x_{2}}f(x)\,dx=\int _{0}^{x_{2}}f(x)\,dx-\int _{0}^{x_{1}}f(x)\,dx$

Wenn Sie den Flächeninhalt in Richtung der negativen $x$ dann zusammenzufassen, was aussieht wie ein positiver Flächeninhalt als negativ zählt. Mit anderen Worten, wenn $x_{1}>x_{2}$ dann, selbst wenn der Funktionswert ist immer positiv, dann sind die Integral auswertet auf einen negativen Funktionswerte, also:

$\int _{x_{1}}^{x_{2}}f(x)\,dx=-\int _{x_{2}}^{x_{1}}f(x)\,dx$

Bitte lesen Sie w: Fundamentalsatz der Analysis. wieder.

Mehr Physik

Für eine unterschiedliche Beschleunigung, wie in einer einfachen harmonischen Bewegung, die Standardnotation für die zweite Ableitung der Verschiebung $x$ von Zeit $t$ (die Beschleunigung) ist:

$a(t)={\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}$

Die Standardnotation für die Doppelintegral ist:

$\int _{0}^{t}\int _{0}^{t}a(t)\,dt\,dt=x(t)$

Die zweite Ableitung und das Doppelintegral sind natürlich, inverse Funktionen voneinander. Die Doppel-Integral wird selten als solche in Infinitesimalrechnung I ausgedrückt, aber es wird häufig verwendet, in Infinitesimalrechnung II und später.

Natürlicher Logarithmus und Exponentialfunktion

Die Hyperbel y=1/x (rote Kurve) und der Flächeninhalt von x=1 bis 6 (in orange schattiert). Dieser Flächeninhalt entspricht dem natürlichen Logarithmus von 6.

Graph der Funktion des natürlichen Logarithmus.

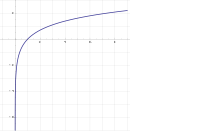
Die Fläche unter der Kurve von $x=0$ zu $x=1$ für $y={\frac {1}{x}}$ ist unendlich. Dies ist das Sonderfall in der Leistungsregel für das Integral der $y=x^{n}$, wo $n=(-1)$. Das bestimmte Integral, dass der natürliche Logarithmus ist, durch die folgende Definition, die endliche Menge, die die Differenz zweier unendlich Flächeninhalt ist. Die Technik für dieses Problem ist nicht in $x=0$. Der natürliche Logarithmus ist die Fläche unter der Kurve $y={\frac {1}{x}}$ in $x=1$:

$\ln(x_{1})=\int _{1}^{x_{1}}{\frac {1}{x}}\,dx.$

Die dreifache ist:

Steigung	Funktionswerte	Flächeninhalt
${\frac {1}{x}}$	$\ln x$	$x\ln x-x$

Die natürliche Exponentialfunktion $y=e^{x}$

Die base des natürlichen Logarithmus ist die mathematische Konstante $e$. Es ist die $x$ Funktionswerte des Punktes $(x,1)$ auf dem natürlichen Logarithmus-Kurve. Wenn man will von $e$ als eine Grenze zu denken, eine Annäherung des exponentiellen Wachstums (wie ein Bankkonto mit der Verbindung täglich Zinsen) beteiligt ist, dann:

$=\lim _{x\to 0}(1+x)^{\frac {1}{x}}$

$e$ verwendet wird ausführlich in den Studien von w: exponentielles Wachstum und exponentiellen Abfall. Die Steigung und der Flächeninhalt (mit Ausnahme der Nicht-Null-Integrationskonstante) der Kurve der w: Exponentialfunktion $y=e^{x}$ sind bemerkenswert, beide Identitäten:

Steigung	Funktionswerte	Flächeninhalt
$e^{x}$	$e^{x}$	$e^{x}-1$

Auf dieser Kurve an dem Punkt, $(a,e^{a})$ in Standard Notation Infinitesimalrechnung:

${\frac {d}{dx}}e^{x}=e^{e}in$

$\int _{0}^{a}e^{x}\,dx=e^{a}-1$

$e$ ist ein bemerkenswert kraftvolle Zahl. Es erscheint in w: Eulersche Formel:

$e^{ix}=\cos x+i\sin x$

die ausführlich in fortgeschrittenen Engineering-Disziplinen verwendet wird, aber ach, das ist über den Rahmen der Infinitesimalrechnung I.

Andere Regeln der Differenzierung und Integration

Es gibt einige andere Regeln über die Macht Regel, die Infinitesimalrechnung I umfasst. Diese Regeln sind hilfreich bei der Einsicht Bereitstellung und Infinitesimalrechnung Person spart Zeit und Mühe.

Differenzierung Regeln

h ( x + Δx ) als die Fläche eines Rechtecks

• W: Produktregel - Betrachten wir die Fläche eines Rechtecks ​​mit Seiten $x(t)$ und $y(t)$, das gegenüber der x- auf den beiden Seiten wächst Achse und y-Achse. Die Gegend ist $A(t)=x(t)y(t)$. Das Wachstum der Flächeninhalt ist
  • Das Wachstum entlang der gegenüberliegenden Seite der x-Achse
  • Das Wachstum entlang der gegenüberliegenden Seite der y-Achse
  • Das kleine Rechteck in der Ecke gegenüber $(0,0)$

Das führt zu:

$xdA=({\frac {d}{dt}}y)+({\frac {d}{dt}}x)y+({\frac {d}{dt}}x)({\frac {d}{dt}}y)$

${\frac {d}{dt}}A=x(dy)+(dx)y+(dx)(dy)$

aber als $dx$ und $dy$ sind infinitesimals und das Produkt von ihnen verschwindet, so ist das Wachstum:

${\frac {d}{dt}}A=x(dy)+(dx)y$

${\frac {d}{dt}}(xy)=x(dy)+(dx)y$

• W: Kettenregel - Nicht so einfach, sichtbar zu machen, aber die Mathematik ist leicht zu merken. Ein einfacher Weg, um teilweise die Kettenregel überprüfen, ist die Kettenregel anzuwenden, um die Ableitung von $(x^{2})^{3}$ und überprüfen zu berechnen, dass es die gleichen Ergebnisse wie bei der Berechnung der Ableitung von direkt die Anwendung Macht Regel $x^{6}$.
• W: Quotientenregel - verwendet werden, können entweder die Produktregel oder der Kettenregel leicht unter Beweis gestellt.
• W: Implizite Funktion # Implizite Differenzierung - mit Kettenregel

Integration Regeln

• W: Integration durch Substitution - ähnlich der Kettenregel
• W: Partielle Integration (fortgeschrittenes Thema nicht in Infinitesimalrechnung I enthalten, aber leicht zu visualisieren)

Andere Infinitesimalrechnung I Themen

Infinitesimalrechnung I Incudes:

• W: Extremwert - zu finden, wo die Ableitung gleich Null, manchmal in der Optimierung, wie die Minimierung Engineering oder finanziellen Kosten verwendet
• W: Kritischer Punkt (Mathematik) - (? Oder unendlich) ein Ort, wo die Ableitung null oder nicht definiert ist
• W: Krümmung von Kurven - folgt das Vorzeichen der zweiten Ableitung
• Funktionen, die x in seiner haben w: Nenner kann w: Asymptotes.
• Manchmal ist es einfacher, die integral in Bezug auf y zu berechnen, anstatt x, dh horizontale Rechtecke anstatt vertikale Rechtecke oder $\int f(y)\,dy$ verwenden.

Einige spätere Themen

Infinitesimalrechnung kann in vielerlei Hinsicht über angewendet werden, was leicht sichtbar gemacht werden kann und darüber hinaus, was in den meisten Infinitesimalrechnung I Kurse abgedeckt ist:

• Andere Koordinatensysteme, zB w: Polarkoordinaten und w: Kugelkoordinaten Systeme.

Weiterführende Informationen

• Kurs:Analysis (Osnabrück 2014-2016)/Teil I

Referenzen

Zitiert Texte

• Strang, Gilbert (1991), Calculus, Wellesley-Cambridge Press, I.S.B.N 978-0-9614088-2-4
  • https://ocw.mit.edu/ans7870/resources/Strang/Edited/Calculus/Calculus.pdf
  • https://books.google.com/books?id=OisInC1zvEMC

Externe Links

• Derivative Calculator