Dynamische Datenstrukturen

Auf dieser Seite wird es eine Einführung in die dynamischen Datenstrukturen geben. Unter dynamischen Datenstrukturen verstehen wir Datenstrukturen bei denen man Elemente löschen und hinzufügen kann, eine interne Ordnung (z.B. Sortierung) vorliegt und diese Ordnung unter Änderungen aufrecht erhalten bleibt. Ein Beispiel sind Lineare Datenstrukturen und Sortierung. Bei unsortierte Liste sind Änderung einfach, aber Zugriff aufwändig. Bei einer Neusortierung einer Liste sind Änderung schwierig, aber Zugriff einfach. Bei Trade-of ist eine “intelligente Datenstruktur” gesucht, die Änderungen und Zugriffe einfach, sprich effizient, halten. Viele dynamische Datenstrukturen nutzen Bäume als Repräsentation.

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 8.5 zu finden.

Bäume

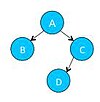
In diesem Kapitel werden Bäume als kurzen Einschub behandelt. Ein Baumelement e ist ein Tupel $e=(v,\lbrace e_{1},...,e_{n}\rbrace )$ mit v vom Wert e und $\lbrace e_{1},...,e_{n}\rbrace$ sind die Nachfolger, bzw. Kinder von e. Ein Baum T ist ein Tupel $T=(r,\lbrace e_{1},...,e_{n}\rbrace )$ mit r als Wurzelknoten (ein Baumelement) und $\lbrace e_{1},...,e_{n}\rbrace$ als Knoten (Baumelemente) des Baumes mit $r\in \lbrace e_{1},...,e_{n}\rbrace$ und für alle $e_{i}=(v_{i},K_{i})~und~e_{j}=(v_{j},K_{j})\in \lbrace e_{1},...,e_{n}\rbrace ~gilt~K_{i}\bigcap K_{j}=\emptyset$

Man spricht von einem geordneten Baum, wenn die Reihenfolge der Kinder $\lbrace e_{1},..,e_{n}\rbrace$ eines jeden Elements $e=(v,\lbrace e_{1},...,e_{n}\rbrace )$ festgelegt ist (schreibe dann $(e_{1},...,e_{n})$ statt $\lbrace e_{1},...,e_{n}\rbrace ).$

Beispiel

$T=(v_{4},\lbrace v_{1},v_{2},v_{3},v_{4},v_{5}\rbrace )$

$v_{1}=(1,\lbrace \rbrace )$

$v_{2}=(2,\lbrace v_{1},v_{3}\rbrace )$

$v_{3}=(3,\lbrace \rbrace )$

$v_{4}=(4,\lbrace v_{2},v_{5}\rbrace )$

$v_{5}=(5,\lbrace \rbrace )$

$T'=(v_{4},\lbrace v_{2},v_{5}\rbrace )$

$v_{2}=(2,\lbrace v_{5}\rbrace )$

$v_{4}=(4,\lbrace v_{2},v_{5}\rbrace )$

$v_{5}=(5,\lbrace \rbrace )$

T' ist kein Baum, da $v_{4}~und~v_{2}$ ein gemeinsames Kind haben.

Begriffe

Ein Pfad folgt über Kanten zu verbundenen Knoten, dabei existiert zu jedem Knoten genau ein Pfad von der Wurzel. Ein Baum ist immer zusammenhängend und zyklenfrei.

Das Niveau der jeweiligen Ebene entspricht immer der jeweiligen Länge des Pfades. Die Höhe eines Baumes entspricht dem größten Niveau+1.

Anwendungen

Man benutzt Bäume beispielsweise zur Darstellung von Hierarchien, wie Taxonomien, oder für Entscheidungsbäume. Bäume werden oft genutzt um sortierte, dynamische oder lineare Datenstrukturen zu repräsentieren, da Einfüge-und Löschoperationen leicht so definiert werden können, dass die Sortierung beibehalten wird. Ein Baum kann auch als Datenindex genutzt werden und stellt so eine Alternative zu Listen und Arrays dar.

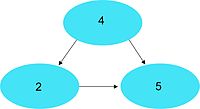
Hier wird beispielsweise nach der 5 gesucht und der Baum wird als Suchbaum genutzt.

Man kann auch einen Baum aus Termen bilden. Der Term (3+4) * 5 + 2 * 3 gibt folgenden Baum:

Atomare Operationen auf Bäumen

Zu den Operationen zählen lesen mit

root(): Wurzelknoten eines Baums
get(e): Wert eines Baumelements e
children(e): Kinderknoten eines Elements e
parent(e): Elternknoten eines Elements e

und schreiben mit

set(e,v): Wert des Elements e auf v setzen
addChild(e,e’): Füge Element e’ als Kind von e ein (falls geordneter Baum nutze addChild(e,e’,i) für Index i)
del(e): Lösche Element e (nur wenn e keine Kinder hat)

Spezialfall: Binärer Baum als Datentyp

 
class TreeNode<K extends Comparable<K>>{
          
       K key;
       TreeNode<K> left = null; 
       TreeNode<K> right = null;
         
       public TreeNode(K e) {key = e; }
       public TreeNode<K> getLeft() {return left; } 
       public TreeNode<K> getRight()  {return right; }
       public K getKey() {return key; }
         
       public void setLeft(TreeNode<K> n) {left = n;}
       public void setRight(TreeNode<K> n) {right = n;} 

         ...
         
 }

Beispiel

TreeNode<Character> root = new TreeNode<Character>(‘A‘);

TreeNode<Character> node1 = new TreeNode<Character>(‘B‘);

TreeNode<Character> node2 = new TreeNode<Character>(‘C‘);

TreeNode<Character> node3 = new TreeNode<Character>(‘D‘);

root.setLeft(node1);

root.setRight(node2);

node2.setLeft(node3);

Typische Problemstellungen

Als typische Problemstellung haben wir zum einen die Traversierung, zum Anderen das Löschen eines inneren Knotens und die daraus folgende Re-strukturierung des Baumes und das Suchen in Bäumen.

Traversierung

Bäume können visuell gut dargestellt werden. Manchmal ist jedoch eine Serialisierung der Elemente eines Baumes nötig. Man kann die Elemente eines Baumes durch Preorder-Aufzählung, Inorder-Aufzählung, Postorder-Aufzählung oder Levelorder-Aufzählung eindeutig aufzählen.

Bei der Traversierung werden systematisch alle Knoten des Baumes durchlaufen.

Preorder (W-L-R): $A\to B\to D\to E\to C\to F\to G$

Inorder (L-W-R): $D\to B\to E\to A\to F\to C\to G$

Postorder (L-R-W): $D\to E\to B\to F\to G\to C\to A$

Levelorder: $A\to B\to C\to D\to E\to F\to G$

Traversierung mit Iteratoren

Bei der Traversierung sind Iteratoren erlaubt. Diese werden schrittweise abgearbeitet und es werden Standardschleifen für die Baumdurchläufe verwendet.

 for  (Integer i : tree) 
              System.out.print(i);

Dabei ist es allerdings notwendig, dass der Bearbeitungszustand zwischengespeichert wird.

public class BinarySearchTree<K extends Comparable<K>>
      implement Iterable<K> {

   public static final int INORDER = 1;  
   public static final int PREORDER = 2;
   public static final int POSTORDER = 3;
   public static final int LEVELORDER = 4;

   private int iteratorOrder;
    ...

  public void setIterationOrder(int io) {
      if (io < i || io > 4)
          return;
      iteratorOrder = io;
  }
 public Iterator<K> iterator() {
     switch (iterationOrder) { 
         case INORDER:
            return new InorderIterator<K>(this);
         case PRORDER:
            return new PreorderIterator<K>(this);
         case POSTORDER:
            return new PostorderIterator<K>(this);
         case LEVELORDER:
            return new LevelorderIterator<K>(this);
         default:
            return new InorderIterator<K>(this);
     }
 }

Preorder Traversierung

Bei der Preorder Traversierung wird der aktuelle Knoten zuerst behandelt und dann der linke oder rechte Teilbaum.

static class TreeNode<K extends Comparable<K>> {
  ...
  public void traverse() {
      if (key==null)
          return;
      System.out.print(” ” + key);
      left.traverse();
      right.traverse();   
  }

Preorder Iteratoren

Der Wurzelknoten wird auf den Stack gelegt, anschließend der rechte Knoten und dann der linke Knoten.

 class PreorderIterator<K extends Comparable <K>>
         implements Iterator<K> {

     java.util.Stack<TreeNode<K>> st =
         new java.util.Stack<TreeNode<K>>();

     public PreorderIterator(BinarySearchTree<K> tree){
           if (tree.head.getRight() != nullNode)
                st.push(tree.head.getRight());
                
     }
  public boolean hasNext() { 
          return !st.isEmpty();
  } 
  
   public K next(){ 
       TreeNode<K> node = st.pop();
       K obj = node.getKey(); 
       node = node.getRight();
       if(node != nullNode) {
          st.push(node);  //rechten Knoten auf den Stack
       }
       node = node.getLeft(); 
       if(node != nullNode) {
          st.push(node);  //linken Knoten auf den Stack
       } 
       return obj;
   } 
}

Inorder Traversierung

Bei der Inorder Traversierung wird zuerst der linke Teilbaum behandelt, dann der aktuelle Knoten und dann der rechte Teilbaum. Als Ergebnis erhält man den Baum in sortierter Reihenfolge.

static class TreeNode<K extends Comparable<K>> {
  ...
  public void traverse() {
      if (key==null)
          return;
      left.traverse();
      System.out.print(” ” + key);
      right.traverse();   
  }

Inorder Iteratoren

Der Knoten head hat immer einen rechten Nachfolger. Es wird vom Wurzelknoten begonnen alle linken Knoten auf den Stack zu legen.

 class InorderIterator<K extends Comparable <K>>
         implements Iterator<K> {

     java.util.Stack<TreeNode<K>> st =
         new java.util.Stack<TreeNode<K>>();

     public InorderIterator(BinarySearchTree<K> tree) {
           TreeNode<K> node = tree.head.getRight();
           while (node != nullNode) {
                st.push(node);
                node = node.getLeft();
           }
    }
  public boolean hasNext() {
          return !st.isEmpty();
  }
  
   public K next(){
       TreeNode<K> node = st.pop();
       K obj = node.getKey();
       node = node.getRight();  //rechten Knoten holen
       while (node != nullNode) {
          st.push(node);
          node = node.getLeft();  //linken Knoten auf den Stack
       }
       return obj;
   }

}

Postorder Traversierung

Bei der Postorder Traversierung wird zuerst der linke und der rechte Teilbaum behandelt und dann der aktuelle Knoten. Dies kann beispielsweise genutzt werden, um einen Baum aus Termen, entsprechend der Priorität der Operatoren, auszuwerten.

static class TreeNode<K extends Comparable<K>> {
  ...
  public void traverse() {
      if (key==null)
          return;
      left.traverse();
      right.traverse();   
      System.out.print(” ” + key);
  }

Levelorder Iteratoren

Der Wurzelknoten wird in der Warteschlange eingefügt. Dann wird zuerst der linke und dann der rechte Knoten in die Warteschlange eingefügt. In dieser Implementierung wird die queue als LinkedList repräsentiert. Dies ist jedoch beliebig.

 class LevelorderIterator<K extends Comparable <K>>
         implements Iterator<K> {

   //Wurzelknoten in die Warteschlange (queue) einfügen
   java.util.Queue<TreeNode<K>> q =
         new java.util.LinkedList<TreeNode<K>>();

   public LevelorderIterator(BinarySearchTree<K> tree){
         TreeNode<K> node = tree.head.getRight();
         if (node != nullNode)
                q.addLast(node);}
  
   public K next(){
       TreeNode<K> node = q.getFirst();
       K obj = node.getKey();
       if (node.getLeft() != nullNode)
            q.addLast(node.getLeft());
       if (node.getRight() != nullNode)
            q.addLast(node.getRight());
       return obj;
   }
}

Bäume in Java

In Java gibt es keine hauseigene Implementierung für allgemeine Bäume. Einige Klassen (TreeMap, TreeSet) benutzen Bäume zur Realisierung anderer Datenstrukturen. Andere Klassen (JTree) benutzen Bäume als Datenmodell zur Visualisierung.

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14 zu finden.

Binäre Suchbäume

Auf dieser Seite werden die binären Suchbäume behandelt. Er ermöglicht einen schneller Zugriff auf Daten mit dem Aufwand O(log n) unter geeigneten Voraussetzungen. Des weiteren ermöglicht er effiziente Sortierung von Daten, durch Heapsort und effiziente Warteschlangen. Der binäre Suchbaum dient als Datenstruktur für kontextfreie Sprachen. In der Computergrafik sind Szenengraphen oft (Beinahe-)Bäume. Bei Informationssysteme dienen binäre Suchbäume zur Datenindizierung und Anfrageoptimierung.

Operationen

Auf Suchbäumen können die Operationen Suchen von Elementen, Einfügen von Elementen und Entfernen von Elementen angewandt werden, wobei letztere zwei voraussetzen, dass die Ordnung der Schlüssel erhalten bleibt.

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14 zu finden.

Suchen

Ein binärer Suchbaum kann für viele Anwendungen eingesetzt werden.

Hier ist der Baum ein Datenindex und eine Alternative zu Listen und Arrays. Beispielsweise kann dieser Baum als Suchbaum verwendet werden und nach "5" gesucht werden.

Bei der Anwendung von Bäumen zur effizienten Suche gibt es pro Knoten einen Schlüssel und ein Datenelement und die Ordnung der Knoten erfolgt anhand der Schlüssel. Bei einem binärer Suchbaum enthält der Knoten k einen Schlüsselwert k.key. Alle Schlüsselwerte im linken Teilbaum k.left sind kleiner als k.key und alle Schlüsselwerte im rechten Teilbaum k.right sind größer als k.key. Die Auswertung eines Suchbaums sieht wie folgt aus:

Vergleich des Suchschlüssels mit Schlüssel der Wurzel
Wenn kleiner, dann in linken Teilbaum weiter suchen
Wenn größer, dann in rechtem Teilbaum weiter suchen
Sonst gefunden/nicht gefunden

static class  TreeNode<K extends Comparable<K>>{
         
       K key;
       TreeNode<K> left = null;
       TreeNode<K> right = null;
        
       public TreeNode(K e) {key = e; }
       public TreeNode<K> getLeft() {return left; }
       public TreeNode<K> getRight()  {return right; }
       public K getKey() {return key; }
        
       public void setLeft(TreeNode<K> n) {left = n;}
       public void setRight(TreeNode<K> n) {right = n;}

         ...
        
 }

Knotenvergleich

class  TreeNode<...> { 
          ...

     public int compareKeyTo(K k) {
           return (key == null ? -1: 
                        key.compareTo(k));
     }
         ...
    
    
 }

Rekursives Suchen

protected  TreeNode<K>
         recursiveFindNode(TreeNode<K>  n, k){ 
          /* k wird gesucht */

          if (n!= nullNode) {
              int cmp = n.compareKeyTo(k.key);
              if (cmp == 0)
                  return n;
              else if (cmp > 0)
                  return 
                     recursiveFindNode(n.getLeft(),k);
              else 
                  return 
                     recursiveFindNode(n.getRight(),k);
          }
          else
                return null;
 }

Iteratives Suchen

protected  TreeNode<K> iterativeFindNode(TreeNode<K> k){ 
          /* k wird gesucht */
          TreeNode<K> n = head.getRight();
          while (n!= nullNode) {
              int cmp = n.compareKeyTo(k.key);
              if (cmp == 0)
                  return n;
              else 
                  n = (cmp > 0 ? 
                      n.getLeft(): n.getRight());
           }
           return null;
 }

Suchen des kleinsten Elements

protected  K findMinElement(){ 
          TreeNode<K> n = head.getRight();
          while (n.getLeft() != nullNode) 
              n = n.getLeft();
          return n.getKey();
}

Suchen des größten Elements

protected  K findMaxElement(){ 
          TreeNode<K> n = head.getRight();
          while (n.getRight() != nullNode) 
              n = n.getRight();
          return n.getKey();
}

Eine weitere Anwendungsmöglichkeit ist der Baum aus Termen. Wir haben den Term $(3+4)\cdot 5+2\cdot 3$ als Baumdarstellung sieht es so aus:

Bei der Auswertung müssen die Operatoren auf die beiden Werte der Teilbäume angewandt werden.

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.3 zu finden.

Einfügen

Das Finden der Einfügeposition erfolgt durch Suchen des Knotens, dessen Schlüsselwert größer als der einzufügende Schlüssel ist und der keinen linken Nachfolger hat oder durch Suchen des Knotens, dessen Schlüsselwert kleiner als der einzufügende Schlüssel ist und der keinen rechten Nachfolger hat. Das Einfügen erfolgt prinzipiell in 2 Schritten. Im ersten Schritt wird die Einfügeposition gesucht, sprich der Blattknoten mit dem nächstkleineren oder nächstgrößerem Schlüssel. Im zweiten Schritt wird ein neuer Knoten erzeugt und als Kindknoten des Knotens aus Schritt eins verlinkt. Wenn in Schritt eins der Schlüssel bereits existiert, dann wird nicht erneut eingefügt.

Programm in Java

 /* Einfügeposition suchen */
public boolean  insert(K k){ 
          TreeNode<K> parent = head;
          TreeNode<K> child = head.getRight();
          while (child != nullNode) {
              parent = child;
              int cmp = child.compareKeyTo(k);
              //Schlüssel bereits vorhanden
              if (cmp == 0)
                  return false;
              else if (cmp > 0)
                  child = child.getLeft();
              else
                  child = child.getRight();
           }
/* Neuen Knoten verlinken */  
  TreeNode<K> node = new TreeNode<K>(k);
            node.setLeft(nullNode);
            node.setRight(nullNode);
            if (parent.compareKeyTo(k) > 0)
                  parent.setLeft(node);
            else
                  parent.setRight(node);
            return true;

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.3.2 zu finden.

Löschen

Zuerst wird das zu löschendes Element gesucht, der Knoten k. Nun gibt es drei Fälle

k ist Blatt: löschen
k hat ein Kind: Kind „hochziehen“
k hat zwei Kinder: Tausche mit weitest links stehenden Kind des rechten Teilbaums, da dieser in der Sortierreihenfolge der nächste Knoten ist und entferne diesen nach den Regeln 1. oder 2.

Ein Schlüssel wird in drei Schritten gelöscht. Im ersten Schritt wird der zu löschende Knoten gefunden. Im zweiten Schritt wird der Nachrückknoten gefunden. Dafür gibt es mehrere Fälle. Im Fall 1 handelt es sich um einen externen Knoten, sprich ein Blatt, ohne Kinder. Dabei wird der Knoten durch einen nullNode ersetzt. Im Fall 2a gibt es nur einen rechten Kindknoten, dabei wird der gelöschte Knoten durch den rechten Kindknoten ersetzt. Im Fall 2b gibt es nur einen linken Kindknoten und der gelöschte Knoten wird durch diesen ersetzt. Im Fall 3 gibt es einen internen Knoten mit Kindern rechts und links. Dabei wird der gelöschte Knoten durch den Knoten mit dem kleinstem (alternativ größtem) Schlüssel im rechten (alternativ linken) Teilbaum ersetzt. im dritten und letzten Schritt wird nun der Baum reorganisiert. Während dem Löschen kann sich die Höhe von Teilbäumen ändern.

Programm in Java

 /* Knoten suchen */
public boolean  remove(K k){ 
          TreeNode<K> parent = head;
          TreeNode<K> node = head.getRight();
          TreeNode<K> child = null;
          TreeNode<K> tmp = null;
          while (node != nullNode) {
              int cmp = node.compareKeyTo(k);
              //Löschposition gefunden
              if (cmp == 0)
                 break;
              else {
                 parent = node;
                 node = (cmp > 0 ?
                      node.getLeft() : node.getRight());
             }
         }
         //Knoten k nicht im Baum
         if (node == nullNode)
            return false;
/* Nachrücker finden */
    if (node.getLeft() == nullNode  &&
            Node.getRight() == nullNode)  //Fall 1
         child = nullNode;
     else if (node.getLeft() == nullNode)  //Fall 2a
           child = node.getRight();
     else if (node.getRight() == nullNode)  //Fall 2b
           child = node.getLight();
          ...   
  //Fall 3
  else {
       child = node.getRight();
       tmp = node;
       while (child.getLeft() != nullNode) {
            tmp = child;
            child = child.getLeft();
       }
       child.setLeft(node.getLeft());
       if (tmp != node) {
            tmp.setLeft(child.getRight());
            child.setRight(node.getRight());
       }
  } 
/* Baum reorganisieren */
        if (parent.getLeft() == node)
                 parent.setLeft(child)
        else 
                 parent.setRight(child);
        return true;
      ...

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.3.2 zu finden.

Implementierung

Ein binärer Suchbaum ist eine häufig verwendete Hauptspeicherstruktur und ist besonders geeignet für Schlüssel fester Größe, z.B. numerische wie int, float und char[n]. Der Aufwand von O(log n) für Suchen, Einfügen und Löschen ist garantiert, vorausgesetzt der Baum ist balanciert. Später werden wir lernen, dass die Gewährleistung der Balancierung durch spezielle Algorithmen gesichert wird. Des weiteren sind größere, angepasste Knoten für Sekundärspeicher günstiger, diese nennt man B-Bäume. Für Zeichenketten benutzt man als Schlüssel variable Schlüsselgröße, sogenannte Tries.

public class   
      BinarySearchTree<K extends Comparable<K>>
           implements Iterable<K> {
         
          ...

    static class TreeNode<K extends Comparable<K>> {
         K key;
         TreeNode<K> left = null;
         TreeNode<K> right = null;
 
         ...
    
    }
 }

Die Schlüssel müssen Comparable-Interface, d.h. compareTo()-Methode, implementieren, da der Suchbaum auf Vergleichen der Schlüssel basiert. Der Baum selbst implementiert Iterable-Interface, d.h. iterator()-Methode, um Traversierung des Baums über Iterator zu erlauben (später Baumtraversierung).TreeNode und alles weitere werden als innere Klassen implementiert. Dadurch werden Zugriff auf Attribute und Methoden der Baumklasse erlaubt. Eine Besonderheit der Implementierung sind die „leeren“ Pseudoknoten head und nullNode zur Vereinfachung der Algorithmen (manchmal „Wächter“ / „sentinel“ genannt). Grundlegende Algorithmen sind

Suchen
Einfügen
Löschen

Implementierung mit Pseudoknoten

Wir vereinbaren an dieser Stelle, dass man auf dem Kopf kein getRight() anwenden kann.

public class   
      BinarySearchTree<K extends Comparable<K>>
           implements Iterable<K> {
         
          ...

       pulic BinarySearchTree(){
            head = new TreeNode<K>(null);
            nullNode = new TreeNode<K>(null);
            nullNode.setLeft(nullNode);
            nullNode.setRight(nullNode);
            head.setRight(nullNode);
       }
         ...
    
    
 }

Das Ziel der Implementierung ist, die Reduzierung der Zahl an Sonderfällen. Im head würde das Einfügen oder Löschen des Wurzelknotens spezielle Behandlung in der Baum-Klasse erfordern. Der nullNode erspart den Test, ob zum linken oder zum rechten Teilknoten navigiert werden kann. Des weiteren ist im NullNode ein einfaches Beenden der Navigation (z.B. Beenden der Rekursion) möglich.

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.2.1 zu finden.

Weitere Aspekte

Die Komplexität der Operation hängt von der Höhe ab. Der Aufwand für die Höhe des Baumes beträgt O(h). Die Höhe eines ausgeglichenen binären Baumes ist h=ld(n) für Knoten. Bei eines ausgeglichenen oder balancierten Baum unterscheiden sich zum einen der rechte und linke Teilbaum eines jeden Knotens in der Höhe um höchstens 1 und zum anderen unterscheiden sich je zwei Wege von der Wurzel zu einem Blattknoten höchstens in um 1 in der Länge. Rot-Schwarz Bäume und AVL Bäume benötigen einen Ausgleich nach dem Einfügen und Löschen.

Entartung von Bäumen

Ungünstige Einfüge- oder Löschreihenfolge führt zu extremer Unbalanciertheit. Im Extremfall wird der Baum zur Liste, dann haben die Operationen eine Komplexität von O(n). Beispiel:

for (int i = 0; i < 10; i++)
tree.insert(i);

Vermeiden kann man dies durch spezielle Algorithmen zum Einfügen und Löschen, z.B. mit Rot-Schwarz-Bäumen und AVL-Bäumen.