Kurs:Algorithmen und Datenstrukturen/Vorlesung/Graphen Druckversion
Typen von Graphen und Anwendungen
[Bearbeiten]In diesem Kapitel werden Graphen behandelt. Ein Graph ist das mathematische Modell eines Netzwerks bestehend aus Knoten und Kanten. Graphen haben einen vielfältigen Einsatz. So kommen sie bei Verbindungsnetzwerken (Bahnnetz, Flugververbindungen, Straßenkarten, ...), Verweisen (WWW, Literaturverweise, Wikipedia, symbolische Links, ...), Technischen Modellen (Platinen-layout, finite Elemente, Computergrafik) und Software Reengineering und - dokumentation zum Einsatz. Bäume und Listen sind spezielle Graphen.
Ungerichteter Graph
[Bearbeiten]Es gibt verschiedene Typen von Graphen. Der ungerichtete Graph ist beispielsweise eine Straßenverbindung, eine Telefonnetz oder ein soziales Netzwerk. Ein ungerichteter Graph ist ein Tupel G=(V,E). Wir haben eine endliche Menge V von Knoten (Vertices) und eine Menge E von Kanten (Edges), die aus ungeordneten Paaren aus V besteht. Es gilt, dass und jedes ist eine zweielementige Teilmenge der Knotenmenge . Im ungerichteten Graphen gibt es keine Schleifen, das heißt es gibt keine Kanten die von einem Knoten zu sich selbst laufen. Außerdem gibt es keine mehrfachen Kanten zwischen zwei Knoten, Parallelkanten genannt.
Hier können zum Beispiel die kürzesten Wege bei sozialen Netzwerken wie Facebook berechnet werden.
Spezielle Graphen
[Bearbeiten]Sei ein Graph.
G heißt planar, falls er ohne Überschneidungen der Kanten in der Ebene gezeichnet werden kann.
G heißt vollständig, falls
G heißt regulär, falls alle Knoten denselben Grad haben
G heißt bipartit, falls und
- keine zwei Knoten in sind adjazent
- keine zwei Knoten in sind adjazent
Beispiele
[Bearbeiten]Dieser Graph ist sowohl planar, regulär als auch vollständig.

Dieser Graph ist jedoch nur regulär und vollständig.

Hier handelt es sich nur um einen regulären Graphen.

Dies ist ein Beispiel für einen bipartiten Graph.

Gerichteter Graph
[Bearbeiten]Der gerichtete Graph ist beispielsweise eine Förderanlage oder ein Kontrollfluss in Programmen. Der gerichtete Graph (auch Digraph) ist ein Tupel G=(V,E) mit V als endliche Menge von Knoten und E einer Menge von Kanten, geordneten Paaren aus V. Jedes ist nun ein Tupel e=(a,b) mit . Schleifen der Form (a,a) sind nun erlaubt. Dazu ist (a,b) eine andere Kante als (b,a). Der Unterschied zwischen (a,b) und {a,b} besteht darin, dass das Tupel (a,b) geordnet ist. Die Reihenfolge kann nicht verändert werden. Hingegen ist {a,b} eine Menge, in der die Reihenfolge der Elemente keine Rolle spielt.
Gerichtete Graphen werden zum Beispiel als Web-Graph (Google`s PageRank) benutzt. Aber auch in der Scientometrie kommen sie zum Einsatz bei der Impact Faktoren Berechnung. Bei Datenstrukturen im Semantik Web werden gerichtete Graphen zum Speichern von Daten genutzt.
Gerichtete und ungerichtete Graphen
[Bearbeiten]Ein ungerichteter Graph kann in einen gerichteten Graphen transformiert werden, indem jede ungerichtete Kante {v,w} durch zwei gerichtete Kanten (v,w) und (w,v) ersetzt wird. Dann ist beispielsweise der Zusammenhang identisch mit dem starken Zusammenhang. Dazu haben gerichtete Graphen eine größere Ausdrucksstärke und daher wird "Graph" oft als Synonym für einen Digraph verwendet.
Gewichteter Graph
[Bearbeiten]Ein ungerichteter gewichteter Graph ist beispielsweise eine Flugverbindung mit Meilen oder Kosten, ein Straßennetz mit Kilometern oder ein Rohrsystem mit Durchfluss.
Ein gerichteter gewichteter Graph ist beispielsweise ein Straßennetz mit Einbahnstraßen, Rohre mit Ventilen oder ein Förderband.
Der Graph ist ein Paar G=(V,E) und wir haben eine Kantengewichtsfunktion g. Daraus erhalten wir G=(V,E,g) mit . Der Graph kann gerichtet oder ungerichtet sein und die Kantengewichte müssen nicht notwendigerweise natürliche Zahlen sein.
Ungerichtete gewichtete Graphen kommen zum Beispiel bei der Navigation beim Berechnen des kürzesten Weges zum Einsatz.
Gerichtete gewichtete Graphen kommen bei der Optimierung in der Telekommunikation zum Einsatz.
Hypergraph
[Bearbeiten]Es gibt aber noch viele weitere Varianten von Graphen wie Multigraphen oder Hypergraphen.
Ein Hypergraph ist ein Paar G=(V,E) mit einer Menge von Knoten V und einer Menge von Hyperkanten .
Definitionen
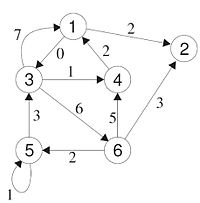
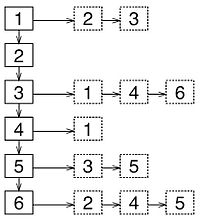
[Bearbeiten]Hier werden allgemeine Definitionen bezüglich der Graphen behandelt. Dazu werden immer wieder Beispiele gebracht, die sich auf folgende Graphen beziehen. Dabei gilt je nach Beispiel G=(V,E) entweder für den ungerichteten oder den gerichteten Graphen.
Adjazenz
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Zwei Knoten heißen adjazent, falls .
Hier heißt v auch Nachbar von w.
Beispiel:
- Knoten 1 und 3 sind adjazent
Gerichteter Graph
[Bearbeiten]Zwei Knoten heißen adjazent, falls oder .
Für heißt w Nachfolger von v und v Vorgänger von w.
Beispiele:
- Knoten 1 ist Vorgänger zu Knoten 3
- Knoten 4 ist Nachfolger zu Knoten 6
Inzidenz
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Eine Kante ist inzident zu einem Knoten , falls oder .
Gerichteter Graph
[Bearbeiten]Eine Kante ist inzident zu einem Knoten , falls oder .
Grad
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Der Grad (engl. degree) eines Knotens ist die Anzahl seiner inzidenten Kanten, das heißt: .
Beispiel:
- Der Grad von Knoten 4 ist 3
Gerichteter Graph
[Bearbeiten]Der Eingangsgrad (engl. in-degree) eines Knotens ist die Anzahl seiner Vorgänger: .
Der Ausgangsgrad (engl. out-degree) eines Knotens ist die Anzahl seiner Nachfolger: .
Beispiele:
- Der Eingangsgrad von Knoten 3 ist 2
- Der Ausgangsgrad von Knoten 3 ist 3
Weg
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Ein Weg W ist eine Sequenz von Knoten mit für die gilt:
Beispiel:
- (1,3,5,6,3,4) ist ein Weg
Gerichteter Graph
[Bearbeiten]Ein (gerichteter) Weg W ist eine Sequenz von Knoten .
Beispiel:
- (1,3,6,5,5,3,1) ist ein (gerichteter) Weg
Pfad
[Bearbeiten]Ein Weg W heißt Pfad, falls zusätzlich gilt . Das heißt, der Weg enthält keine doppelten Knoten. Diese Definition gilt sowohl für ungerichtete als auch gerichtete Graphen.
Beispiel:
- (1,4,6,5) ist ein Pfad
Kreis
[Bearbeiten]Ein Weg P heißt Kreis, falls . Dazu ist ein Kreis K elementar, falls . Der Kreis enthält also keine doppelten Knoten bis auf den Anfangs- und den Endpunkt. Diese Definition gilt sowohl für ungerichtete als auch gerichtete Graphen.
Beispiel:
- (1,3,4,6,3,4,1) ist ein Kreis
- (3,4,6,3) ist ein elementarer Kreis
Länge
[Bearbeiten]Die Länge eines Weges ist die Anzahl der durchlaufenen Kanten. Die Länge eines Pfades ist also n-1. Diese Definition gilt sowohl für ungerichtete als auch gerichtete Graphen.
Beispiel:
- Die Länge von (3,4,6,3,4,1) ist 4
- Die Länge von (1,3,6) ist 2
Teilgraph
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Ein Graph heißt Teilgraph von G, falls .
Beispiel:
- G'=({3,4,6},{{3,4},{4,6}}) ist ein Teilgraph von G
Gerichteter Graph
[Bearbeiten]Ein Graph heißt Teilgraph von G, falls und .
Beispiel:
- ist ein Teilgraph von .
Erreichbarkeit
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Ein Knoten heißt erreichbar von einem Knoten , falls ein Weg existiert mit und .
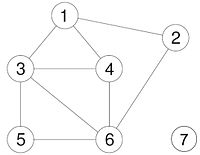
Beispiele:
- Knoten 6 ist erreichbar von Knoten 1
- Knoten 7 ist nicht erreichbar von Knoten 1
Gerichteter Graph
[Bearbeiten]Ein Knoten heißt erreichbar von einem Knoten , falls ein Weg existiert mit und .
Beispiele:
- Knoten 6 ist erreichbar von Knoten 1
- Knoten 5 ist nicht erreichbar von Knoten 2
Zusammenhang
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]G heißt (einfach) zusammenhängend, falls für alle gilt, dass w von v erreichbar ist
Ein Teilgraph von G heißt Zusammenhangskomponente von G, falls G' zusammenhängend ist und kein Teilgraph von G existert mit .
Beispiele:
- G ist nicht zusammenhängend
- Der Teilgraph ist eine Zusammenhangskomponente von G
- Der Teilgraph ist eine Zusammenhangskomponente von G
Gerichteter Graph
[Bearbeiten]G heißt (stark) zusammenhängend, falls für alle gilt, dass w von v und v von w erreichbar ist.
Ein Teilgraph von G heißt starke Zusammenhangskomponente von G, falls stark zusammenhängend ist und kein Teilgraph von G existiert mit .
Beispiel:
- Der Teilgraph mit und ist eine starke Zusammenhangskomponente von .
Repräsentation von Graphen
[Bearbeiten]Auf dieser Seite wird die Repräsentation von Graphen behandelt. Wir fragen uns wie effizient die Datenstruktur für Graphen ist.
Kanten- und Knotenlisten
[Bearbeiten]Bei durchnummerierten Knoten erfolgt eine einfache Realisierung. Historisch gesehen ist es die erste verwendete Datenstruktur. Außerdem ist sie als Austauschformat geeignet und die Auflistung ist nach Knoten oder nach Kanten sortiert.
Beispiel Kantenliste
[Bearbeiten]
Gegeben ist eine Kantenliste für
Die erste Zahl (6) steht für die Knotenzahl. Die zweite Zahl (11) steht für die Kantenzahl. Die weiteren Paare (1,2 ; 1,3...) stehen für die Kanten.
6,11,1,2,1,3,3,1,4,1,3,4,3,6,5,3,5,5,6,5,6,2,6,4
Beispiel Knotenliste
[Bearbeiten]
Gegeben ist eine Knotenliste für
6,11,2,2,3,0,3,1,4,6,1,1,2,3,5,3,2,4,5 Die Teilfolge 2,2,3 bedeutet, dass der Knoten 1 den Ausgangsgrad 2 hat und herausgehende Kanten zu den Knoten 2 und 3.
Vergleich Kanten-und Knotenliste
[Bearbeiten]Falls ein Graph mehr Kanten als Knoten hat (=„Normalfall“),benötigen Knotenlisten weniger Speicherbedarf als Kantenlisten. Das bedeutet für die Kantenlisten gilt und für die Knotenliste gilt .
Adjazenzmatrix
[Bearbeiten]Adjazenz bedeutet berühren oder aneinander grenzen. Hier werden die Graphen als Boole‘sche Matrix dargestellt. 1-Einträge werden für direkte Nachbarschaften verwendet. A ist eine Adjazenzmatrix für den Graph
Beispiel
[Bearbeiten]
Eigenschaften
[Bearbeiten]Bei ungerichteten Graphen reicht eine Halbmatrix (ein Dreieck) aus. Bei gewichteten Graphen werden Gewichte statt Boolsche Werte genutzt. Der Vorteil einer Adjazenzmatrix ist, dass einige Graphenoperationen als Matrixoperation möglich sind. So ist sie beispielsweise durch iterierte Matrixmultiplikation erreichbar und besitzt schöne Eigenschaften für die mathematische Analyse.
So sieht die Darstellung als Dreiecksmatrix aus. Die Diagonale kann ebenfalls weggelassen werden, wenn Schleifen verboten sind.
Adjazenzliste
[Bearbeiten]Wir haben eine Liste der 3b oder alternativ ein Array. Pro Knoten werden die von ihm ausgehenden Kanten als Liste, welche besonders geeignet für dünn besetzte Matrizen sind, oder als Array von Zeigern dargestellt. Der Graph wird durch |V|+1 verkettete Listen realisiert. In Adjazenzlisten sind dynamische Erweiterungen im Sinne verketteter Listen erlaubt. Knotenlisten können natürlich auch als verkettete Listen realisiert werden.

Speicherbedarf
[Bearbeiten]Seien n=|V| und m=|E|. Benötigt werden insgesamt Listenelemente. ag(i) ist die Anzahl der Nachbarn von i (gerichtet).
Transformation zwischen den Darstellungen
[Bearbeiten]Die vorgestellten Realisierungsvarianten sind äquivalent. Jede Darstellung kann in jede andere ohne Informationsverlust transformiert werden. Dafür wird die eigene Darstellung ausgelesen und anschließend die andere Darstellung erzeugt. Der Aufwand dieser Transformationen variiert von O(n+m) bis wobei im schlechtesten Fall gilt. tritt immer auf, wenn eine naive Matrixdarstellung beteiligt ist. Nicht naive Darstellungen sind für sehr dünn besetzte Matrizen nötig.
Komplexitätsbetrachtung
[Bearbeiten]Bei Kantenlisten ist das Einfügen von Kanten (Anhängen von zwei Zahlen) und von Knoten (Erhöhung der ersten Zahl um 1) besonders günstig. Das Löschen von Kanten zieht das Verschieben der nachfolgenden Kanten mit sich und die Knoten müssen neu nummeriert werden.
Bei Knotenlisten ist das Einfügen von Knoten, also die Erhöhung der ersten Zahl und das Anhängen einer 0, günstig.
Bei der Matrixdarstellung ist das Manipulieren von Kanten sehr effizient ausführbar. Der Aufwand beim Knoteneinfügen hängt von der Realisierung ab. Im worst case wird die Matrix in eine größere Matrix kopiert.
Bei Adjazenzlisten gibt es unterschiedlichen Aufwand, je nachdem, ob die Knotenliste ein Feld mit Direktzugriff oder eine verkettete Liste mit sequenziellem Durchlauf realisiert.
| Operation | Kantenliste | Knotenliste | Adjazenzmatrix | Adjazenzliste |
| Einfügen Kanten | Beta(1) | O(n+m) | O(1) | O(1)/O(n) |
| Löschen Kanten | O(m) | O(n+m) | O(1) | O(n) |
| Einfügen Knoten | O(1) | O(1) | O(1) | |
| Löschen Knoten | O(m) | O(n+m) | O(n+m) |
Das Löschen eines Knotens impliziert für gewöhnlich auch das Löschen der dazugehörigen Kanten.
Datenstrukturen für Graphen
[Bearbeiten]Auf dieser Seite werden die Datenstrukturen für Graphen behandelt. In Java gibt es keine hauseigene Graphimplementierung, aber es gibt diverse Pakete für verschiedene Anwendungen.
- Jung (http://jung.sourceforge.net)
Graph<Integer, String> g = new SparseMultigraph<Integer, String>();
g.addVertex((Integer)1);
g.addVertex((Integer)2);
g.addEdge("Edge1", 1, 2);
- Neo4j (http://www.neo4j.org)
GraphDatabaseService= new
"GraphDatabaseFactory().newEmbeddedDatabase(“PATH”);
Transaction tx = graphDb.beginTx();
try{
Node firstNode = graphDb.createNode();
Node secondNode = graphDb.createNode();
Relationship relationship = firstNode.createRelationshipTo(secondNode,
… );
tx.success();
}finally{
tx.finish();
}
Die allgemeine Schnittstelle für die Vorlesung ist:
public interface Graph {
public int addNode();
public boolean addEdge (int orig, int dest);
}
Implementierung Adjazenzliste
[Bearbeiten] public class AdjazenzListGraph implements Graph {
private int [][] adjacencyList=null;
//Knoten hinzufügen:
public int addNode() {
int nodeNumber = (adjacencyList ==null)?0: adjacencyList.length;
int [][] newAdjacencyList= new int [nodeNumber+1][];
//alte adjacencyList kopieren
for (int i=0; i< nodeNumber; i++)
newAdjacencyList [i]=adjacencyList[i];
//neuer Knoten hat noch keine Kanten
newAdjacencyList[nodeNumber] =null;
adjacencyList=newAdjacencyList;
return nodeNumber+1;
}
//Kante hinzufügen:
public boolean addEdge (int orig, int dest){
int nodeNumber = (adjacencyList == null)? 0: adjacencyList.length;
if (orig > nodeNumber || dest > nodeNumber || orig < 1 || dest < 1 )
return false;
if (adjacencyList[orig-1] != null)
for (int n : adjacencyList[orig-1])
//Kante bereits vorhanden?
if (n==dest) return false;
//Erste Kante am Knoten orig?
if ( adjacencyList[orig-1] == null ) {
adjacencyList [orig-1] = new int[1];
adjacencyList[orig-1][0]=dest;
}
else {
int[] newList= new int[adjacencyList[orig-1].length+1];
System.arraycopy(adjacencyList[orig-1],0,newList,0,adjacencyList[orig-1].length);
newList[adjacencyList[orig-1].length]=dest;
adjacencyList [orig-1]=newList;
}
return true;
}
}
Breitensuche
[Bearbeiten]Auf dieser Seite behandeln wir die Breitensuche. Wir fragen uns wie man die Knoten eines Graphen effizient aufzählt. Die Lösung ist der Breitendurchlauf ( Breadth-First-Search, BFS). Dabei werden die Knoten eines Graphen nach der Entfernung vom Zielknoten aufgezählt. Eine andere Methode ist der Tiefendurchlauf, zu dem kommen wir aber später. Bei dem Breitendurchlauf für ungerichtete Graphen gibt es eine Warteschlange als Zwischenspeicher. Farbmarkierungen beschreiben den Status der Knoten. Weiß bedeutet er ist unbearbeitet, grau bedeutet er ist in Bearbeitung und schwarz bedeutet, dass er abgearbeitet ist. Pro Knoten wird die Entfernung zum Startknoten berechnet. Bei der Initialisierung wird der Startknoten in eine Warteschlange eingefügt, die Farbe auf grau gesetzt und die Entfernung mit 0 berechnet. Die anderen Knoten haben eine unendliche Entfernung und sind weiß markiert.
Beim Breitendurchlauf wird der aktuelle Knoten k aus der Warteschlange genommen und schwarz gefärbt. Alle von k aus erreichbaren weißen Knoten werden grau gefärbt, die Entfernung ist der Entfernungswert von k+1 und sie werden in der Warteschlange aufgenommen.
Algorithmus
[Bearbeiten]Ergänzung zum Graph-Interface:
public interface Graph{
public int addNode();
public boolean addEdge(int orig, int dest);
public Collection<Integer> getChildren(int node);!
}
Breitendurchlauf als Iterator:
public class BfsIterator implements Iterator<Integer>{
private Graph g;
private Queue<Integer> q;
private Set<Integer> visited;
public BfsIterator(Graph g, int s){
this.g = g;
this.q = new LinkedList<Integer>();
q.add(s);
this.visited = new HashSet<Integer>();
}
public boolean hasNext() { return !this.q.isEmpty(); }
public Integer next() {
Integer n = this.q.poll();
for(Integer m: this.g.getChildren(n))
if(!this.visited.contains(m) && !this.q.contains(m))
this.q.add(m);
this.visited.add(n);
return n;
}
}
Ausgabe aller Knoten:
//Sei g ein Graph
Iterator<Integer> it = new BfsIterator(g,1);
while(it.hasNext())
System.out.println(it.next());
Analyse
[Bearbeiten]Theorem der Terminierung
[Bearbeiten]Die Breitensuche terminiert nach endlicher Zeit
Theorem der Korrektheit
[Bearbeiten]Ist G zusammenhängend, so werden alle Knoten von G genau einmal besucht.
Theorem der Laufzeit
[Bearbeiten]Ist G=(V,E) zusammenhängend und ist die Laufzeit von getChildren linear in der Anzahl der Kinder, so hat die Breitensuche eine Laufzeit von O(|V| + |E|).
Tiefendurchlauf
[Bearbeiten]Auf dieser Seite wird der Tiefendurchlauf behandelt. Der Tiefendurchlauf wird auch Depth-First-Search, oder abgekürzt DFS, genannt. Die Knoten werden aufgezählt indem vom Startknoten aus ein Pfad so weit wie möglich verfolgt wird und bei Bedarf ein Backtracking durchgeführt wird. Bei Tiefendurchlauf werden die Knoten ebenfalls farblich markiert. Weiß bedeutet der Knoten ist noch nicht bearbeitet, grau bedeutet der Knoten ist in Bearbeitung und schwarz bedeutet der Knoten ist bereits fertig abgearbeitet.
Ergänzung zum Graph Interface:
public interface Graph{
public int addNode();
public boolean addEdge(int orig, int dest);
public Collection<Integer> getChildren(int node);
public Collection<Integer> getNodes();
}
Algorithmus
[Bearbeiten]enum Color {WHITE, GRAY, BLACK};
Map<Integer,Color> color = new HashMap<Integer,Color>();
Map<Integer,Integer> pi = new HashMap<Integer,Integer>();
Map<Integer,Integer> f = new HashMap<Integer,Integer>();
Map<Integer,Integer> d = new HashMap<Integer,Integer>();
int time = 0;
color speichert die Farbe, bzw. den Bearbeitungszustand eines Knotens.
pi speichert den Vorgänger eines Knotens beim Durchlauf.
f speichert den Zeitpunkt des Bearbeitungsbeginns eines Knotens.
d speichert den Zeitpunkt des Bearbeitungsendes eines Knotens.
public void dfs(Graph g){
for(Integer n: g.getNodes())
color.put(n, Color.WHITE);
for(Integer n: g.getNodes())
if(color.get(n).equals(Color.WHITE))
dfsVisit(g,n);
}
public void dfsVisit(Graph g, Integer n){
color.put(n, Color.GRAY);
time++;
d.put(n, time);
for(Integer m: g.getChildren(n)){
if(color.get(m).equals(Color.WHITE)){
pi.put(m, n);
dfsVisit(g,m);
}
}
color.put(n, Color.BLACK);
time++;
f.put(n, time);
}
Vorgehen
[Bearbeiten]Der Tiefendurchlauf ist ein rekursiver Abstieg. Pro Knoten haben wir zwei Werte und deren Farbwerte. Beginn der Bearbeitung ist d und Ende der Bearbeitung ist f. Der rekursive Aufruf erfolgt nur bei weißen Knoten, die Terminierung der Rekursion ist hier garantiert. Die Ausführung von DFS resultiert in einer Folge von DFS-Bäumen. Der erste Baum wird aufgebaut bis keine Knoten mehr hinzugefügt werden können. Anschließend wird ein unbesuchter Knoten gewählt und fortgefahren. Bei den Kanten des aufgespannten Baumes ist der Zielknoten beim Test weiß. An den B-Kanten ist der Zielknoten beim Test grau. Hierbei handelt es sich um Back Edges oder Rückkanten im aufgespannten Baum. Eine mit B markierte Kante zeigt einen Zyklus an. Bei F Kanten werden beim Test schwarze Knoten gefunden, dessen Bearbeitungsintervall ins Intervall des aktuellen bearbeiteten Knotens passt. Es handelt sich hierbei um Forward Edges bzw. Vorwärtskanten in dem aufgespannten Baum. Bei C Kanten haben wir schwarze Zielknoten v, dessen Intervalle nicht in das aktuelle Intervall passen (d[u]>f[v]). Hierbei handelt es sich um Cross Edges, eine Kante die zwei aufgespannte Bäume verbindet.
Beispiel
[Bearbeiten]Die Notation an den Knoten ist dabei durch <Beginn der Bearbeitung d> / <Ende der Bearbeitung f> gegeben.
Analyse
[Bearbeiten]Theorem der Terminierung
[Bearbeiten]Die Tiefensuche terminiert nach endlicher Zeit.
Theorem der Korrektheit
[Bearbeiten]Es werden alle Knoten von G genau einmal besucht.
Theorem der Laufzeit
[Bearbeiten]Ist sowohl die Laufzeit von getChidlren linear in der Anzahl der Kinder als auch getNodes linear in der Anzahl der Knoten, so hat die Tiefensuche eine Laufzeit von O(|V|+|E|).
Anwendung
[Bearbeiten]Der Tiefendurchlauf wird beispielsweise bei dem Test auf Zyklenfreiheit verwendet. Damit ein Graph zyklenfrei ist, darf kein Kreis K in dem Graph G vorhanden sein. Deshalb basiert dieser Test auf dem Erkennen von Back Edges. Er ist effizienter als beispielsweise die Konstruktion einer transitiven Hülle. Die Tiefensuche wird aber auch beim topologischen Sortieren verwendet. Topologisch bedeutet sortieren nach Nachbarschaft, nicht nach totaler Ordnung.
Topologisches Sortieren
[Bearbeiten]Auf dieser Seite wird das topologische Sortieren behandelt. Wir fragen uns, wie Knoten unter Berücksichtigung von Abhängigkeiten aufgezählt werden können bei gegebenem azyklischem gerichteten Graph. Zur Anwendung kommt diese Sortierung bei Scheduling bei kausalen und zeitlichen Abhängigkeiten, zum Beispiel bei der Netzplantechnik. Mathematisch liegt hier eine Konstruktion einer totalen Ordnung aus einer Halbordnung vor.
Beispiel
[Bearbeiten]Die sorgfältige Mutter legt ihrem Kind morgens die Kleidungsstücke so auf einen Stapel, dass das Kind nur die Kleidungsstücke vom Stapel nehmen und anziehen muss und dann richtig gekleidet ist. Hierfür legt sie die Reihenfolgebedingungen fest:
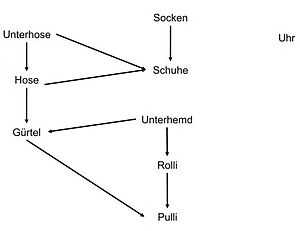
Unterhose vor Hose
Hose vor Gürtel
Unterhemd vor Gürtel
Gürtel vor Pulli
Unterhemd vor Rolli
Rolli vor Pulli
Socken vor Schuhen
Hose vor Schuhen
Uhr: egal
DFS erstellt die topologische Ordnung on the fly. Das Sortieren nach f-Wert (invers) ergibt eine korrekte Reihenfolge. Statt der expliziten Sortierung nach f werden beim Setzen des f-Wertes die Knoten vorne in eine verkettete Liste eingehängt.

18 Socken
16 Unterhose
15 Hose
14 Schuhe
10 Uhr
8 Unterhemd
7 Gürtel
5 Rolli
4 Pulli
Alternativer Durchlauf:
Berechnung kürzester Wege
[Bearbeiten]Auf dieser Seite wird die Berechnung der kürzesten Wege behandelt.
Gegeben ist ein (Di-)Graph mit einer Gewichtsfunktion: . Der Pfad durch G ist eine Liste von aneinanderstoßenden Kanten . Das Gewicht oder die Länge eines Pfades ist die Aufsummierung der einzelnen Kantengewichte. . Die Distanz zweier Punkte d(u,v) ist das Gewicht des kürzesten Pfades von u nach v.
Es existieren verschiedene kürzeste Wege Probleme.
SPSP: Single pari shortest path
- Eingabe: Graph G, Startknoten s, Endknoten t
- Ausgabe: Distanz d(s,t)
SSSP: Single source shortest paths
- Eingabe: Graph G, Startknoten s
- Ausgabe: Distanzen d(s,v) für alle Knoten v
APSP: All-pairs shortest paths
- Eingabe: Graph G
- Ausgabe: Distanzen d(v,w) für alle Knoten v,w
Auf den nächsten Seiten lernen wir zwei Algorithmen zum Berechnen des kürzesten Weges kennen.
Dijkstra Algorithmus
[Bearbeiten]Auf dieser Seite wird der Dijkstra Algorithmus behandelt. Der Dijkstra Algorithmus wird zur Berechnung des kürzesten Weges benutzt (SSSP). Der Algorithmus stammt von 1959. Es erfolgt eine iterative Erweiterung einer Menge von günstig erreichbaren Knoten. Der Greedy Algorithmus hat eine ähnliche Breitensuche ist aber nur für nichtnegative Gewichte. Er berechnet iterativ verfeinert die Distanzwerte d(v,w) und es gibt eine Prioritätswarteschlange zum Herauslesen des jeweils minimalen Elements.
Priority Queues
[Bearbeiten]Eine Priority‐Queue P ist eine dynamische Datenstruktur, die (mindestens) die folgenden Operationen unterstützt:
- P.add(Element): Element hinzufügen
- P.poll(): Minimalste Element zurückgeben
- P.contains(Element): Enthält P das Element?
Die Ordnung zur Sortierung muss dabei vorab definiert sein.
Ein Heap kann beispielsweise zur Implementierung einer Priority‐Queue benutzt werden (add‐Operation ist dann O(log n), poll‐Operation O(log n), und contains‐Operation ist O(n)). Benutzt man zusätzlich zum Heap noch einen binären Suchbaum auf denselben Element so ist auch contains in O(log n) realisierbar.
Priority Queue in Java
[Bearbeiten]class DijkstraComparator implements Comparator<Integer>{
Map<Integer,Integer> d = new HashMap<Integer,Integer>();
public DijComparator(Map<Integer,Integer> d){
this.d = d;
}
public int compare(Integer o1, Integer o2) {
return d.get(o1).compareTo(d.get(o2));
}
}
Ist d eine Map “Knoten”‐>”Aktueller Distanzwert von s aus”, so ist PriorityQueue<Integer> queue = new PriorityQueue<Integer>(g.getNumberOfNodes(),new DijkstraComparator(d)); eine Priority‐Queue, die bei iterativen Aufruf queue.poll() immer das Element mit dem minimalsten d‐Wert zurückliefert.
Idee
[Bearbeiten]- Initialisiere alle Distanzwerte von s zu v mit ∞ (und von s zu s mit 0)
- Initialisiere eine Priority‐Queue Q mit allen v
- Extrahiere das minimale Element aus Q
- Aktualisiere alle Distanzwerte der Nachfolger von in Q:
- Ist es günstiger über zu einem Knoten w zu kommen?
- Falls ja setzte d(s,w)=d(s,)+y(,w)
- 5. Wiederhole bei 3 solange Q noch Elemente hat
Algorithmus in Java
[Bearbeiten]Map<Integer,Integer> dijkstra(Graph g, int s){
Map<Integer,Integer> d = new HashMap<Integer, Integer>();
PriorityQueue<Integer> queue = //Initialisiere Priority-Queue entsprechend
for(Integer n: g){
if(!n.equals(s)){
d.put(n, Integer.MAX_VALUE);
queue.add(n);
}
}
d.put(s, 0);
queue.add(s);
while(!queue.isEmpty()){
Integer u = queue.poll();
for(Integer v: g.getChildren(u)){
if(queue.contains(v)){
if(d.get(u) + g.getWeight(u,v) < d.get(v){
d.put(v, d.get(u) + g.getWeight(u,v));
}
}
}
}
return d;
}
Algorithmus
[Bearbeiten]algorithm Dijkstra (G,s)
- Eingabe: Graph G mit Startknoten s
- for each Knoten u V[G] -s do // Initialisierung
- D[u] :=
- od;
- D[s]:= O; PriorityQueue Q := V;
- while not isEmpty (Q) do
- U := extractMinimal (Q);
- for each v ZielknotenAusgehenderKanten (u) Q do
- if D[u] + ((u,v)) < D[v] then // Entfernung über u nach v kleiner als aktuelle Entfernung D[v]
- D[v] := D[u] + ((u,v));
- adjustiere Q an neuen Wert D[v]
- fi
- if D[u] + ((u,v)) < D[v] then // Entfernung über u nach v kleiner als aktuelle Entfernung D[v]
- od
- od
- for each Knoten u V[G] -s do // Initialisierung
Initialisierung
[Bearbeiten]

Der Iterationsstart ist korrekt für die Tiefe 0. Wir nehmen an, dass der vorherige Iterationsschritt korrekt war ( Induktionsbeweis). Der Ein Iterationsschritt ist jeweils die günstigste Verbindung zu einem noch nicht bearbeiteten Knoten hinzunehmen. Da die bisher bearbeiteten Knoten den korrekten Distanzwert haben, ist der neue Distanzwert durch den „günstigsten“ aus dem bisher bearbeiteten Teilgraphen um genau eine Kante hinausgehenden Pfad bestimmt. Jeder Pfad zum Zielknoten dieses Pfades, der um mehr als eine Kante aus dem bearbeiteten Bereich hinausgeht, ist teurer als die gewählte, da Kosten mit zusätzlich hinzu genommenen Kanten nicht sinken können.
Analyse
[Bearbeiten]Terminierungstheorem
[Bearbeiten]Der Algorithmus von Dijkstra terminiert für eine endliche Eingabe nach endlicher Zeit.
Beweis
[Bearbeiten]In jedem Schritt der while‐Schleife wird ein Element aus queue entfernt und die Schleife endet sobald queue leer ist. Jeder Knoten hat nur endliche viele Kinder, deswegen ist auch die Laufzeit der inneren for‐Schleife endlich.
Korrektheitstheorem
[Bearbeiten]Sind alle Kantengewichte nicht‐negativ, so enthält d am Ende die Distanzwerte von s zu allen anderen Knoten.
Beweis
[Bearbeiten]Beachte, dass sobald ein Knoten v aus queue entfernt wird, der Wert für v in d nicht mehr geändert wird.
Zeige nun, dass gilt: Wird v aus queue entfernt, so enthält d den Distanzwert von s nach v. Zeige dies durch Induktion nach i=„Anzahl bisher aus queue entfernter Knoten“:
- i=0: Am Anfang hat queue nur für s einen endlichen Wert gespeichert, alle anderen Werte sind ∞. Der Knoten s wird auch stets zuerst entfernt und der Distanzwert ist 0. Dies ist auch korrekt, da s zu sich selbst Distanz 0 hat und alle anderen Knoten keine geringere Distanz von s aus haben können (da alle Kanten nicht‐negative Gewichte haben).
- i → i+1: Sei v der (i+1)te Knoten, der aus queue entfernt wird.
- Da die bisher bearbeiteten Knoten den korrekten Distanzwert haben, ist der neue Distanzwert durch den „günstigsten“ aus dem bisher bearbeiteten Teilgraphen um genau eine Kante hinausgehenden Pfad bestimmt.
- Jeder Pfad zum Zielknoten dieses Pfades, der um mehr als eine Kante aus dem bearbeiteten Bereich hinausgeht, ist teurer als die gewählte, da Kosten mit zusätzlich hinzugenommenen Kanten nicht sinken können.
Laufzeittheorem
[Bearbeiten]Sei G=(V,E,g) ein gerichteter Graph. Der Laufzeitaufwand von Dijkstras Algorithmus für einen beliebigen Knoten s in G ist O((|E| + |V|) log |V|).
Beweis
[Bearbeiten]Beachte: Wird für die Priority‐Queue beispielsweise ein Heap verwendet, so hat die Operation poll() einen Aufwand von O(log k) (mit k=„Anzahl Elemente in Queue“). Sei |V|=n und |E|=m. Insgesamt: O(n log n) + O(n) + n* O(log n) + m *O(log n) = O((m + n) log n) Durch Benutzung sog. Fibonacci‐Heaps (anstatt normaler Heaps) kann die Laufzeit von O((m + n) log n) verbessert werden zu O(m + n log n)
Nachteile
[Bearbeiten]Der kürzeste Weg wird immer gefunden, aber es werden viele unnötige und sinnlose Wege gegangen. Bei negativen Kanten resultieren auch falsche Ergebnisse.
Bellmann-Ford
[Bearbeiten]Auf dieser Seite wird der Bellmann-Ford Algorithmus behandelt. Bei Dijkstra dürfen nur nichtnegative Gewichte benutzt werden. Doch gibt es auch eine Variante mit negativen Gewichten? Das würde nur bei gerichteten Graphen Sinn machen. Das Problem sind Zyklen mit negativem Gesamtgewicht. Ein Beispiel für Gewinn statt Kosten ist beispielsweise ein Verbindungsnetz mit Bonus Gewinnen für bestimmte Verbindungen um Auslastungen zu erhöhen. Dies ist bei Flügen mit Zwischenstopps der Fall, die oft billiger sind. Dieser Algorithmus löst ebenfalls das SSSP Problem.
Prinzip
[Bearbeiten]Der Algorithmus erfolgt in mehreren Durchläufen. Es wird zunächst die bisher beste mögliche Verbindung bestimmtl, die die um eine Kante länger ist. Der i-te Durchlauf berechnet korrekt alle Pfade vom Startknoten der Länge i. Der längste Pfad ohne Zyklus hat eine Länge kleiner als |V|-1, somit hat man spätestens nach |V|-1 Durchläufen ein stabiles Ergebnis. Sollte das Ergebnis nach |V|-1 Durchläufen nicht stabil sein, so ist ein negativ bewerteter Zyklus enthalten. Hierbei wird das Prinzip der dynamischen Programmierung verwendet.
Algorithmus
[Bearbeiten]algorithm BF(G, s)
Eingabe: ein Graph G mit Startknoten s
D[s] = 0
D[t] = ∞ for all other t
for i := 1 to |V|-1 do
for each (u,v)∈ E do
if D[u]+γ((u,v)) < D[v] then
D[v] := D[u] + γ((u,v))
fi
od
od
Beispiel
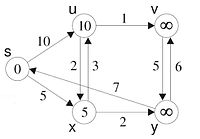
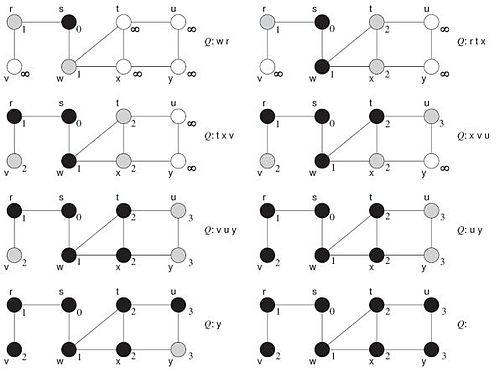
[Bearbeiten]Bei der Initialisierung wird der Startknoten auf den Wert 0 gesetzt und alle weiteren Knoten erhalten den Wert ∞.
Beim ersten Schleifendurchlauf bekommt x den Wert 5 und u den Wert 10 zugewiesen.
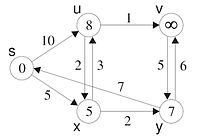
Im zweiten Schleifendurchlauf werden alle weiteren Verbindungen aktualisiert, sowohl von u als auch von x. Dabei ändern sich die Werte von v, y und auch u. Die Änderung an u wird aber erst im nächsten Schritt an v propagiert.
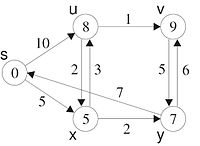
Im dritten, i=3, Schleifendurchlauf verändern sich diesmal nur noch die Werte der Knoten v und y. Der neue Wert aus y berechnet sich durch den vorherigen Wert aus v=11 und der negativ gewichteten Kante -5. Hier wird also die negativ gewichtete Kante (v,y) zur Berechnung von D[y] genutzt.
Im vierten, i=4, Schleifendurchlauf wird nochmals die negativ gewichtete Kante (v,y) zur Berechnung von D[y] genutzt. Das Greedy-Verfahren, das jeden Knoten nur einmal besucht, hätte für y den in jedem Schritt lokal optimalen Pfas gewählt und nicht das beste Ergebnis geliefert.
Analyse
[Bearbeiten]Terminierungstheorem
[Bearbeiten]Der Algorithmus BF(G,s) terminiert für eine endliche Eingabe G in endlicher Zeit.
Beweis
[Bearbeiten]Alle Schleifen sind endlich.
Korrektheitstheorem
[Bearbeiten]Ist G ein Graph, der keinen Zyklus mit negativem Gewicht hat, so enthält D nach Aufruf BF(G,s) die Distanzwerte von s zu allen Knoten.
Beweis
[Bearbeiten]Wir zeigen, dass die folgenden Aussagen Schleifeninvariante der for‐ Schleife (Schleifenvariable i) sind:
- Ist D[v] < ∞, so ist D[v] der Wert eines Pfades von s nach v
- Ist D[v] < ∞, so ist D[v] der kleinste Wert eines Pfades von s nach v mit maximal i Kanten
- D[v] < ∞ gdw. es einen Pfad von s nach v mit gleich oder weniger als i Kanten gibt
Da G keine Zyklen mit negativem Gewicht hat, ist die Länge des längsten kürzesten Pfades maximal |Anzahl Knoten|‐1 (jeder Knoten wird auf diesem Pfad einmal besucht). Also gilt nach dem letzten Schleifendurchlauf nach 2 und 3. die Aussage des Theorems. Wir zeigen diese Aussagen durch Induktion nach i(=#Schleifendurchläufe).
- Bei i=0 gilt vor dem ersten Schleifendurchlauf nur D[s]=0 < ∞. Daraus folgt direkt 1., 2., 3.
- Bei i -> i+1 beweisen wir zunächst Aussage 3.
- War D[v] schon vorher endlich, so gilt die Aussage nach IV.
- Ist D[v] in diesem Schritt auf einen endlichen Wert gesetzt worden, so gab es ein u, so dass D[u] vorher schon endlich war und D[v]=D[u]+γ(u,v). Nach IV gibt es einen Pfad von s nach u der Länge i. Damit gibt es einen Pfad der Länge i+1 von s nach v.
- Umgekehrt wird bei Existenz eines Pfades der Länge i+1 dieser auch gefunden und D[v] auf einen endlichen Wert gesetzt.
- Die Aussage 1 wird dadurch bewiesen, dass nach IV der Wert eines Pfades von s nach u D[u] ist. Wird D[v]=D[u]+γ(u,v) gesetzt so ist somit D[v] der Wert des Pfades von s nach v über u.
- Die Aussage 2 wird dadurch bewiesen, dass nach IV der kleinste Wert eines Pfades von s nach v mit maximal i Kanten D[v] ist. Mache folgende Fallunterscheidung:
- 1.Fall: Es existiere ein Pfad P1 von s nach v mit i+1 Kanten, der minimalen Wert unter allen Pfaden von s nach v mit gleich oder weniger als i+1 Kanten hat. Betrachte den vorletzten Knoten u auf diesem Pfad und den Teilpfad P2 von P1 von s nach u. Dieser Teilpfad hat minimalen Wert unter allen Pfaden der maximalen Länge i von s nach u (ansonsten wäre P1 kein Pfad mit minimalem Wert). Nach IV ist D[u] genau dieser Wert und D[u]+γ(u,v) der Wert von P1, der dann im i+1ten Durchgang aktualisiert wird.
- 2.Fall: Es existiere kein Pfad von s nach v mit i+1 Kanten, der minimalen Wert unter allen Pfaden von s nach v mit gleich oder weniger als i+1 Kanten hat.
- 1. Unterfall: Es existiert kein Pfad von s nach v mit maximal i+1 Kanten. Dann bleibt nach 3. D[v]=∞.
- 2. Unterfall: Es existiert ein Pfad von s nach v mit k<i+1 Kanten, der minimalen Wert unter allen Pfaden von s nach v mit gleich oder weniger als i+1 Kanten hat. Dann ist nach IV D[v] genau dieser Wert und wird im i+1ten Durchgang auch nicht aktualisiert.
Graph mit negativ gewichtetem Zyklus
[Bearbeiten]
Betrachten wir die Situation nach |V|-1 Iterationen. Eine Kante könnte noch verbessert werden genau dann wenn der Graph einen Zyklus negativer Länge enthält. Der Zyklus s,x,u,v,y,s hat die Kosten 5+3+1-5-7=-3. Jeder Durchlauf durch den Zyklus erzeugt also einen Gewinn. Es gibt hier keinen günstigen Pfad endlicher Länge!
Laufzeittheorem
[Bearbeiten]Sei G=(V,E,g) ein gerichteter Graph. Der Laufzeitaufwand vom Algorithmus von Bellmann‐Ford für einen beliebigen Knoten s in G ist O(|V||E|).
Beweis
[Bearbeiten]Einfache Schleifenanalyse.
Floyd-Warshall
[Bearbeiten]Auf dieser Seite wird der Floyd-Warshall Algorithmus behandelt. Der Dijkstras Algorithmus und Bellman-Ford berechnen zu einem gegebenen Startknoten die kürzesten Wege zu allen anderen Knoten (Single Source Shortest Paths – SSSP. Aber wie kann man die kürzesten Wege zwischen zwei Knoten v und w berechnen? Man könnte die bereits kennengelernten Algorithmen für jeden einzelnen Startknoten neu aufrufen, doch das geht auch geschickter. Hier kommt der Floyd-Warshall Algorithmus ins Spiel, welcher das All Pairs Shortest Path Problem löst. Zwar nicht unbedingt effizienter, aber eleganter. Dies geschieht nach dem Prinzip der dynamischen Programmierung.
Problemdefinition
[Bearbeiten]Gegeben ist ein Graph G=(V,E). Wir möchten für jedes Paar den Wert D(v,w) eines kürzesten Pfades finden. Wir nehmen an, dass es keine negativen Kreise gibt.

| D | s | u | v | x | y |
| s | 0 | 8 | 9 | 5 | 4 |
| u | 3 | 0 | 1 | -2 | -4 |
| v | 2 | 10 | 0 | 7 | -5 |
| x | 6 | 3 | 4 | 0 | -1 |
| y | 7 | 15 | 6 | 12 | 0 |
Idee
[Bearbeiten]Die Grundidee des Floyd-Warshall Algorithmus ist, dass wenn ein kürzester Weg von v nach w über k geht, dann gilt:
- ist ein kürzester Weg von v nach k
- ist ein kürzester Weg von k nach w
Im obigen Beispiel gilt folgendes:
Die Umkehrung gilt jedoch nicht. Ist ein kürzester Weg von v nach k und ist ein kürzester Weg von k nach w dann gilt nicht notwendigerweise, dass ein kürzester Weg von v nach w ist!
Im obigen Beispiel bedeutet dies:
- ist nicht der kürzeste Weg!
Jedoch gilt, wenn bekannt ist, dass ein kürzester Weg zwischen v und w nur Knoten aus enthält, so gilt entweder der kürzeste Weg zwischen v und w benutzt nur Knoten aus oder der kürzeste Weg zwischen v und w ist Konkatenation aus dem kürzesten Weg zwischen v und k und dem kürzesten Weg zwischen k und w und beide Wege enthalten nur Knoten aus .
Algorithmus
[Bearbeiten]algorithm FW(G)
Eingabe: ein Graph G
for each v,v‘∈V
D[v,v‘] = γ((v,v‘)) (or ∞)
for each k ∈ V do
for each i ∈ V do
for each j ∈ V do
if D[i,k]+D[k,j] < D[i,j] then
D[i,j] := D[i,k]+D[k,j]
fi
od
od
od
Beispiel
[Bearbeiten]Initialisiere D mit den Kantengewichten. Nicht vorhandene Kanten haben das Gewicht . Die Kantengewichte zum Knoten selber sind 0. Im folgenden betrachten wir nur Schleifendurchgänge mit

| D | s | u | v | x | y |
| s | 0 | 10 | 5 | ||
| u | 0 | 1 | -2 | ||
| v | 0 | -5 | |||
| x | 3 | 0 | 2 | ||
| y | 7 | 6 | 0 |










| D | s | u | v | x | y |
| s | 0 | 10 | 5 | ||
| u | 0 | 1 | -2 | ||
| v | 0 | -5 | |||
| x | 3 | 0 | 2 | ||
| y | 7 | 17 | 6 | 0 |


| D | s | u | v | x | y |
| s | 0 | 10 | 5 | ||
| u | 0 | 1 | -2 | ||
| v | 0 | -5 | |||
| x | 3 | 0 | 2 | ||
| y | 7 | 17 | 6 | 12 | 0 |

Führt man den Algorithmus weiter durch, kommt man zu folgendem Endergebnis:
| D | s | u | v | x | y |
| s | 0 | 8 | 9 | 5 | 4 |
| u | 3 | 0 | 1 | -2 | -4 |
| v | 2 | 10 | 0 | 7 | -5 |
| x | 6 | 3 | 4 | 0 | -1 |
| y | 7 | 15 | 6 | 12 | 0 |
Analyse
[Bearbeiten]Terminierungstheorem
[Bearbeiten]Der Algorithmus FW(G) terminiert für eine endliche Eingabe G in endlicher Zeit.
Beweis
[Bearbeiten]Alle Schleifen sind endlich.
Korrektheitstheorem
[Bearbeiten]Ist G ein Graph, der keinen Zyklus mit negativem Gewicht hat, so enthält D nach Aufruf FW(G) die Distanzwerte von allen Knoten zu allen anderen Knoten.
Beweis
[Bearbeiten]Betrachte dazu folgende Schleifeninvariante, die äußerste for-Schleife mit der Laufvariablen k): Nach der k-ten Schleifeniteration gilt, dass D[v,w], für alle v,w, der Wert eines kürzesten Pfades ist, der nur Knoten 1,...,k benutzt. Wenn der Algorithmus endet, gilt damit die Aussage des Theorems. Dies zeigen wir durch Induktion.
- k=0 (bei der Initialisierung): Nach der Initialisierung gilt D[v,w]= ∞ gdw. es keine Kante von v nach w gibt. Das bedeutet, dass jeder Pfad zwischen v und w mindestens einen anderen Knoten enthalten haben muss. Ist D[v,w] endlich, so ist dies genau der Wert der Kante. Dann gibt es also einen Pfad, der keine weiteren Knoten beinhaltet.
- k -> k+1: Nach der Induktionsannahme ist D[v,w] der Wert eines kürzestens Pfades, der nur Knoten aus 1,...,k enthält. Im k+1-Schleifendurchgang wird überprüft, ob es einen kürzeren Weg über k+1 gibt und ggfs. aktualisiert. Es wird also genau folgende Gleichung ausgenutzt:
Anschließend ist also D[v,w] der Wert eines kürzestens Pfades, der nur Knoten 1,...,k+1 benutzt.
Ein anderer Ansatz ist dies per Induktion nach der kürzesten Länge eines kürzesten Weges für jedes Knotenpaar (v,w) zu zeigen. Anmerkung: zwischen v und w können mehrere Wege mit minimalem Gewicht existieren, diese können auch unterschiedliche Länge haben. Angenommen zwischen v und w existiert ein kürzester Weg der Länge 1, dann ist der Wert dieses Weges gleich dem Wert der Kante (die existieren muss. Dieser wird in der Initialisierungsphase gesetzt und später nicht mehr geändert. Angenommen zwischen v und w gibt es einen kürzesten Pfad (=minimales Gewicht) der Länge l≥ 2 , dann gibt es einen Knoten k auf diesem Pfad, so dass zum einen der Teilpfad von v nach k ein kürzester Weg von v nach k ist und zum anderen, dass der Teilpfad von k nach w ein kürzester Weg von k nach w ist. Somit haben beide Pfade haben Länge < l, d.h. die Werte D[v,k] und D[k,w] müssen schon korrekt berechnet sein (die Induktionsvoraussetzung greift). Da alle potentiellen “Mi5elknoten” überprüft werden, wird ein geeignetes k gefunden und der Wert D[v,w] aktualisiert.
Laufzeittheorem
[Bearbeiten]Sei G=(V,E,g) ein gerichteter Graph. Der Laufzeitaufwand vom Algorithmus von Floyd‐Warshall auf G ist ).
Beweis
[Bearbeiten]Einfache Schleifenanalyse.
Flussproblem
[Bearbeiten]Auf dieser Seite wird das Flussproblem behandelt. Die Bestimmung des maximalen Flusses muss in vielen logischen Aufgaben angewandt werden. Beispielsweise bei Verteilungsnetzen mit Kapazitäten wie Wasserrohren, Förderbändern oder Paketvermittlungen mit Rechnernetzen. Die Quellen liefert beliebig viele Objekte pro Zeiteinheit und die Senke verbraucht diese. Jede Verbindung hat eine maximale Kapazität c und einen aktuellen Fluss f. Wie hoch ist nun die Übertragungskapazität?
Definition Fluss
[Bearbeiten]Ein Fluss f von nach ist eine Funktion . Für diese Funktion gelten folgende zwei Bedingungen:
- Die Kapazitäten werden eingehalten:
- Was in einen Knoten hereinfließt, muss wieder herausfließen, mit Ausnahme von q und z: , wobei der Vorgänger von v ist und der Nachfolger von v ist.
Einschränkungen der Kapazität der Kanten werden eingehalten, auch bei negativem Fluss:
Außerdem ist der Fluss konsistent. Bei in beiden Richtungen nutzbaren Verbindungen wird als Nettoeffekt nur in eine Richtung gesendet und der entstehende negative Fluss nimmt den korrekten Wert an:
Der Fluss wird für jeden Knoten mit Ausnahme der Quelle q und des Ziels z bewahrt:
Der Wert eines Flusses beträgt:
Gesucht wird der maximale Fluss:
f ist korrekter Fluss von q nach z}
Beispiel
[Bearbeiten]Definiere durch
.
Daraus folgt, dass der Wert des Flusses 6 ist: .

Definiere durch
.
Daraus folgt, dass kein Fluss ist.
Definiere durch
.
Daraus folgt, dass der Wert des Flusses 14 ist: . Damit ist der Fluss maximal.

Ford-Fulkerson
[Bearbeiten]Auf dieser Seite wird der Ford Fulkerson Algorithmus zur Berechnung des maximalen Flusses behandelt.
Berechnung des maximalen Flusses
[Bearbeiten]Der Ford-Fulkerson Algorithmus ist ein effizienter Algorithmus zur Bestimmung eines maximalen Flusses von q nach z. Dabei wird der Greedy Algorithmus mit Zufallsauswahlen gemischt. Hier wird das Prinzip "Füge so lange verfügbare Pfade zum Gesamtfluss hinzu wie möglich" verfolgt. Zuerst soll ein nutzbarere Pfad durch Tiefensuche gefunden werden. Für die Kanten werden dann drei Werte notiert. Zum einen der aktuellen Fluss entlang der Kante. Im initialisierten Graphen ist dieser Wert überall 0. Zudem wird die vorgegebene Kapazität c notiert und die abgeleitete noch verfügbare Restkapazität von c-f.
Algorithmus
[Bearbeiten]initialisiere Graph mit leerem Fluss;
do
wähle nutzbaren Pfad aus;
füge Fluss des Pfades zum Gesamtfluss hinzu;
while noch nutzbarer Pfad verfügbar
Ein nutzbarere Pfad ist ein zyklenfreier Pfad von der Quelle q zum Ziel z, der an allen Kanten eine verfügbare Kapazität hat. Ein nutzbarer Fluss ist das Minimum der verfügbaren Kapazitäten der einzelnen Kanten.
Der nachfolgende Pseudocode realisiert das Problem mit zusätzlichen Rückkanten.
für jede Kante(u,v) füge Kante (v,u) mit Kapazität 0 ein;
initialisiere Graph mit leerem Fluss;
do
wähle nutzbaren Pfad aus;
füge Fluss des Pfades zum Gesamtfluss hinzu;
while noch nutzbarer Pfad verfügbar
Beispiele
[Bearbeiten]
Wir haben einen Graph mit Kapazitäten gegeben

Es wird mit dem Fluss 0 initialisiert. Notation: <aktueller Fluss f> / <Kapazität c> / <verfügbare Kapazität c-f>

Die Auswahl der nutzbaren Pfade geschieht zufällig oder durch geeignete Heuristik. Es gibt auch kürzere Pfade mit höheren Kapazitäten. Die Rückkanten werden mit der Kapazität 0 eingefügt. Die Auswahl eines Pfades geschieht durch Der nutzbare Fluss beträgt 4.

Der Fluss wird aktualisiert. Die Auswahl des Pfades ist nun : . Der nutzbare Fluss beträgt 5.

Der Fluss wird aktualisiert. Die Auswahl des Pfades ist nun : . Der nutzbare Fluss beträgt 3.
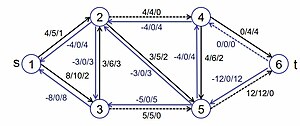
Der Fluss wird aktualisiert. Die Auswahl des Pfades ist nun : . Der nutzbare Fluss beträgt 2.

An dieser Stelle sind keine Kapazitäten mehr über und die Berechnung wir beendet. Der maximale Fluss beträgt 14.
Der Algorithmus kann dabei auf verschiedene Ergebnisse kommen, jedoch ist der maximale Fluss immer gleich. Eine weitere Lösung ist folgende:
Zunächst wird der Pfad mit dem nutzbaren Fluss 5 ausgewählt.

Anschließend wird der Fluss aktualisiert. Im nächsten Schritt wird dann der Pfad gewählt. Ebenfalls ist hier wieder ein nutzbarer Fluss von 5.

Nach der zweiten Aktualisierung ist nur noch ein Pfad vom Start zum Ziel möglich. Also wird der Pfad ausgewählt. Dieser Fluss enthält allerdings nur noch einen nutzbaren Fluss von 4.

Nach dem Aktualisieren des Flusses ist es nicht mehr möglich einen Pfad vom Start zum Ziel zu finden. Damit ist die Berechnung beendet. Wie zuvor berechnet ist der maximale Fluss 14.

Problem: Ungünstige Pfadwahl
[Bearbeiten]Die bisher betrachtete Version des Algorithmus ist nicht immer optimal.
Wählen der Pfad ausgewählt, besitzt dieser Pfad einen nutzbaren Fluss von 5.
Nun wird der Fluss aktualisiert. Daraus folgt, dass keine weitere Pfadwahl mehr möglich ist. Dabei wäre die optimale Lösung über die Pfade und .
Das Problem ist, dass der Fluss nicht zurückgenommen werden kann. Die Lösung dazu ist, dass man entgegengesetzte Flussrichtung durch Rückkanten erlaubt. Auch hier wird wieder der ungünstige Pfad mit einem nutzbaren Fluss von 5 im ersten Schritt ausgewählt.
Anschließend wird der Fluss aktualisiert. Dabei wird der Pfad mit dem nutzbaren Fluss von 5 ausgewählt.
Beim erneuten aktualisieren des Flusses, stellt sich heraus, dass keine weiteren Pfade möglich sind. Damit ist die Berechnung, bei einem maximalen Fluss von 10, beendet.
Analyse
[Bearbeiten]Terminierungstheorem
[Bearbeiten]Sind alle Kapazitäten in G nicht-negativ und rational, dann terminiert der Algorithmus von Ford‐Fulkerson nach endlicher Zeit.
Laufzeittheorem
[Bearbeiten]Ist X der Wert eines maximales Flusses in G=(V,E) und sind alle Kapazitäten in G nicht-negativ und ganzzahlig, so hat der Algorithmus von Ford‐Fulkerson eine Laufzeit von O(|E|X).
Korrektheitstheorem
[Bearbeiten]Sind alle Kapazitäten in G nicht‐negativ und rational, dann berechnet der Algorithmus von Ford‐Fulkerson den Wert eines maximalen Flusses.
Anmerkung
[Bearbeiten]Die Wahl des Pfades beeinflusst die Anzahl benötigter Iteratoren. Bei dem Verfahren von Edmons und Karp muss die Anzahl der Pfade die in einem Graphen G = (V,E) bis zum Finden des maximalen Flusses verfolgt werden, kleiner sein als |V||E|, wenn jeweils der kürzeste Pfad von Quelle q zu Ziel z gewählt wird. Daher kann die Auswahl des nächsten kürzesten Pfades basierend auf einer Variante der Breitensuche erfolgen. Dadurch wird die Laufzeit auf verbessert.
Spannbäume
[Bearbeiten]Auf dieser Seite werden Spannbäume und in diesem Zusammenhang der Algorithmus von Prim behandelt.
Beispiel Kommunikationsnetz
[Bearbeiten]Zwischen n Knotenpunkten soll ein möglichst billiges Kommunikationsnetz geschaltet werden, so dass jeder Knotenpunkt mit jedem anderen verbunden ist, ggf. auf einem Umweg über andere Knotenpunkte. Bekannt sind die Kosten für die direkte Verbindung zwischen und . Alle Kosten seien verschieden und größer Null. Die Modellierung geschieht somit als gewichteter, ungerichteter und vollständiger Graph mit einer Gewichtungsfunktion c.

etc; abgekürzt etc
Problemstellung: Finde minimal aufspannenden Baum
[Bearbeiten]Einige Definitionen für ungerichtete Graphen:
Ein Graph G=(V,E) heißt zusammenhängend, wenn für alle v,w∈V ein Pfad von v nach w in G existiert.
Ein Graph G=(V,E) enthält einen Zyklus, wenn es unterschiedliche Knoten gibt, so dass . Ein Graph G=(V,E) heißt Baum, wenn er zusammenhängend ist und keinen Zyklus enthält.
Ein Graph G’=(V’,E’) heißt Teilgraph von G=(V,E), wenn und .
Ein Graph G’=(V’,E’) heißt induzierter Teilgraph von G=(V,E) bzgl. , wenn
Ein Graph G‘=(V‘,E‘) heißt Spannbaum von G=(V,E), wenn V'=V und G' ein Teilgraph von G und ein Baum ist.
Das Gewicht einen Graphen G=(V,E) ist .
Ein Graph G'=(V',E') ist ein minimaler Spannbaum von G=(V,E), wenn G' ein Spannbaum von G ist und G' unter allen Spannbäumen von G das minimalste Gewicht hat.
Algorithmus von Prim
[Bearbeiten]Der Algorithmus wird schrittweise verfeinert und der Aufbau eines aufgespannten Baumes erfolgt durch das Hinzufügen von Kanten. Das Greedy Muster, also jeweils die Wahl der kostengünstigsten Kante als Erweiterung, wird hier benutzt.
Aufspannender minimaler Baum
[Bearbeiten]//Teilbaum B besteht anfangs aus einem beliebigen Knoten
while [ B noch nicht GV aufspannt ]
do [ suche kostengünstige von B ausgehende Kante ];
[ füge diese Kante zu B hinzu ];
od
Eine Verfeinerung der Suche nach der kostengünstigsten Kante ist notwendig!
Suche nach kostengünstigster Kante
[Bearbeiten]Die intuitive Vorgehensweise erfordert jeweils |W|(|V|-|W|) Vergleiche für ein gegebenes W. Das ganze |V| mal, also eine Gesamtlaufzeit von . Man kann die Suche auf die Teilmengen beschränken, so dass F immer die günstigste aus b ausgehende Kante enthält, wesentlich weniger Kanten hat als |W|(|V|-|W|) und im Verlauf des Algorithmus einfach anpassbar ist.
Wahl von F
[Bearbeiten]Alternativen:
a) F enthält für jeden Knoten v in B die günstigste von v aus B herausführende Kante
b) F enthält für jeden Knoten v außerhalb B die günstigste von v in B hineinführende Kante
Bewertung:
a) Mehrere Kanten können zum gleichen Knoten herausführen – redundant und änderungsaufwändig (bei Wahl dieses Knotens darf er nicht mehr verwendet werden und alle Verbindungen zu diesem Knoten müssen gelöscht werden)
b) Daher: Wahl von b)
Erste Verfeinerung
[Bearbeiten]// Teilbaum B
[ B:= ({ beliebiger Knoten v }, {}) ]
// Menge der Kandidatenkanten F
[ F:= alle nach v führenden Kanten ]
// alle Knoten betrachten
for i := 1 to |V|-1
do [ suche günstigste Kante f=(u,w) in F ];
[ Füge f zu B hinzu (natürlich auch w) ];
[ Aktualisiere F ];
od
F muss nach jedem Durchlauf angepasst werden. Wenn f aus F entfernt wird erkennt man, dass der Teilgraph B tatsächlich ein Baum ist. Nun haben wir den neu verbundenen Knoten w. Jeder noch nicht verbundene Knoten x hat nun eine günstigste Verbindung entweder wie zuvor, oder aber mit dem neu hinzugefügten Knoten w!
Zweite Verfeinerung
[Bearbeiten]// Teilbaum B
[ B:= ({ beliebiger Knoten v },{}) ]
// Menge der Kandidatenkanten F
[ F:= alle nach v führenden Kanten ]
for i := 1 to |V|-1
do
// Sei v∈B, w∈B
[ suche günstigste Kante f=(v,w) in F ];
[ Füge f zu B hinzu ];
// Aktualisiere F
[ Entferne f aus F ];
// x in B, w neuerdings in B, y noch nicht in B
for [ alle Kanten e=(x,y)∈F]
do
if [ c((w,y))<c(e)] then [ Ersetze e durch (w,y) ] fi
od
od
Kommunikationsnetz
[Bearbeiten]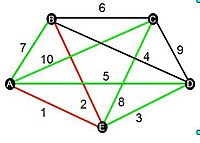
i:
ist am günstigsten
….
Analyse
[Bearbeiten]Terminierungstheorem
[Bearbeiten]Der Algorithmus von Prim terminiert nach endlicher Zeit.
Beweis
[Bearbeiten]Einfache Schleifenanalyse
Laufzeittheorem
[Bearbeiten]Wird für die Implementierung von F ein Fibonacci‐Heap benutzt, so hat der Algorithmus von Prim eine Laufzeit von O(|E| + |V| log |V|).
Korrektheitstheorem
[Bearbeiten]Ist G ein verbundener ungerichteter gewichteter Graph, so berechnet der Algorithmus von Prim einen minimalen Spannbaum von G.
Beweis
[Bearbeiten]Wir betrachten eine einfache Version des Algorithmus.
while [ B noch nicht GV aufspannt ]
do [ suche kostengünstige von B ausgehende Kante ];
[ füge diese Kante zu B hinzu ];
od
Wir beobachten, dass B am Ende ein Spannbaum ist. Jetzt ist noch zu zeigen, dass B am Ende ein minimaler Spannbaum ist.
Sei B‘ ein minimaler Spannbaum von G und B≠B‘. Betrachte den Zeitpunkt in der Hauptschleife, an dem sich die Konstruktion von B von B‘ unterscheidet. Sei e die Kante, die dann zu B hinzugefügt wird. Sei die Menge der Knoten, die schon in B sind und \ Da B‘ ein minimaler Spannbaum ist, gibt es eine Kante e', die mit verbindet. Da im Algorithmus stets eine günstigste Kante gewählt wird, muss gelten g(e)≤g(e‘). Tauschen wir in B‘ die Kante e‘ durch e erhalten wir also einen minimalen Spannbaum, der nicht mehr kostet als B‘, es folgt g(e)=g(e‘). Induktiv folgt damit die Korrektheit.















































































![{\displaystyle D[s]+\gamma (s,u)<D[u]?}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c738ddab1c09a24b922d405a821a042339ef1317)

![{\displaystyle \Rightarrow D[u]=10}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71317c99dbf3d74df30200ee1693f2f3b3b427b5)
![{\displaystyle D[s]+\gamma (s,x)<D[x]?}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1f379f2308dd6ac3b8764fb38919f07e18d61eb)

![{\displaystyle \Rightarrow D[x]=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1b4a0320223418c33a7338081e03f0a4141161)

![{\displaystyle D[x]+\gamma (x,u)<D[u]?}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d4556cb5d2c3bfc966d2ef2ced8ce1efc25af76)

![{\displaystyle \Rightarrow D[u]=8}](https://wikimedia.org/api/rest_v1/media/math/render/svg/331ce6731fa686c7b80487c3ac7454ab4eaa772a)
![{\displaystyle D[y]analog}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c32c7936bdfff2c96f467e84db2fc70c86592a)
























![{\displaystyle D^{V'}[i,j]=fac(x):=\left\{{\begin{array}{ll}\gamma (i,j)&falls~k=0\\min\{D^{V'\backslash \{k\}}[i,j],D^{V'\backslash \{k\}}[i,k]+D^{V'\backslash \{k\}}[k,j]\}&falls~k\geq 1\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33f124e4ecac61a071702f5e26bb81979f2172e9)

![{\displaystyle D^{V'}[i,j]=\left\{{\begin{array}{ll}\gamma (i,j)&{\text{falls}}\ V'=\emptyset \\min\{D^{V'\backslash \{k\}}[i,j],D^{V'\backslash \{k\}}[i,k]+D^{V'\backslash \{k\}}[k,j]\}&{\text{für}}\ k\in V'\end{array}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbaf77bd5703a50998036270ecc76360729ad8fb)



































































