Kurs:Algorithmen und Datenstrukturen/Vorlesung/Laufzeitanalysen Druckversion

Komplexität

Auf dieser Seite wird das Thema Komplexität behandelt. Gegeben ist ein zu lösendes Problem. Es ist wünschenswert, dass der Algorithmus zur Berechnung der Lösung einen möglichst geringen Aufwand hat. Daher wird der Aufwand des Algorithmus (Komplexität) abgeschätzt . Zur Lösung von Problemen einer bestimmten Klasse gibt es einen Mindestaufwand.

Motivierendes Beispiel

Als Beispiel nutzen wir die sequentielle Suche in Folgen. Gegeben ist die Zahl b und n Zahlen, z.B. mit A[0...n-1] mit n>0, wobei die Zahlen verschieden sind. Gesucht ist ein Index $i\in \{0,...,n-1\}~mit~b=A[i]$, falls der Index existiert, sonst ist i = n. Die Lösung für das Problem ist:

i = 0; 
  while (i < n  &&  b != A[i]) 
    i++;

Der Aufwand der Suche hängt nun von der Eingabe ab, d.h vom gewählten Wert n, den Zahlen A[0],...,A[n] und von b. Es gibt zwei Möglichkeiten, eine erfolgreiche oder eine erfolglose Suche. Eine erfolgreiche Suche haben wir, wenn b=A[i] dann ist S=i+1 Schritte. Ist die Suche jedoch erfolglos, dann ist S=n+1 Schritte. Das Problem ist, dass die Aussage von zu vielen Parametern abhängt und unser Ziel ist eine globale Aussage zu finden, die nur von einer einfachen Größe abhängt, z.B. der Länge n der Folge.

Analyse erfolgreiche Suche

Im schlechtesten Fall wird b erst im letzten Schritt gefunden, d.h. b=A[n-1]. Dann wäre S=n. Im Mittel wird die Anwendung mit verschiedenen Eingaben wiederholt. Wenn man beobachtet wie oft b an erster, zweiter,..., letzter Stelle gefunden wird, hat man eine Annahme über die Häufigkeit. Läuft der Algorithmus k mal (k>1), so wird b gleich oft an erster, zweiter,....,letzter Stelle gefunden und somit k/n mal an jeder Stelle. Die Anzahl der Schritte insgesamt für k Suchvorgänge lässt sich folgendermaßen berechnen:

$M={\frac {k}{n}}\cdot 1+{\frac {k}{n}}\cdot 2+...+{\frac {k}{n}}\cdot n$

$={\frac {k}{n}}\cdot (1+2+...+n)$

$={\frac {k}{n}}\cdot {\frac {n\cdot (n+1)}{2}}$

$=k\cdot {\frac {n+1}{2}}$

Für eine Suche benötigt man $S={\frac {M}{k}}$ Schritte Daraus folgt, dass im Mittel ( bei einer Gleichverteilung) $S={\frac {n+1}{2}}$

Asymptotische Analyse

Zur Analyse der Komplexität geben wir eine Funktion als Maß für den Aufwand an. $f:\mathbb {N} \to \mathbb {N}$. Das bedeutet f(n)=a bei Problemen der Größe n beträgt der Aufwand a. Die Problemgröße ist der Umfang der Eingabe, wie z.B. die Anzahl der zu sortierenden oder zu durchsuchenden Elemente. Der Aufwand ist die Rechenzeit( Abschätzung der Anzahl der Operationen, wie z.B. Vergleiche) und der Speicherplatz.

Aufwand für Schleifen

Wie oft wird die Wertezuweisung x=x+1 in folgenden Anweisungen ausgeführt?

 x = x +1

1-mal

  for (i = 1; i <= n; i++)   
    x = x + 1;

n-mal

  for (i = 1; i <= n; i++)
   for (j = 1; j <= n; j++) 
         x = x + 1;

$n^{2}$-mal

Aufwandsfunktion

Die Aufwandsfunktion $f:\mathbb {N} \to \mathbb {N}$ ist meist nicht exakt bestimmbar. Daher wird der Aufwand im schlechtesten Fall und im mittleren Fall abgeschätzt und die Größenordnung ungefähr errechnet.

Vergleich Größenordnung

Funktion	n=100	n=10.000	n=100.000
log n	4,6	9,2	11,5
$n^{2}$	10.000	100.000.000	10.000.000.000
$n^{3}$	1.000.000	$10^{12}$	$10^{15}$

Problemstellung

Wie können wir das Wachstum von Funktionen abschätzen und wie verhalten sich die Funktionen zueinander? Das Ziel ist, die Funktion $t_{i}(n)$ zu wählen, die $f(n)$ nach oben beschränkt.

$f(n)={\frac {1}{3}}~n^{2}$

$t_{1}(n)={\frac {1}{4}}~n^{2}$

$t_{2}(n)=n$

$t_{3}(n)={\frac {1}{3}}~n^{2}+2$

$t_{4}(n)=2^{n}$

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3 zu finden.

O-Notation

Auf dieser Seite wird die O-Notation behandelt. Bei der O-Notation werden die asymptotischen oberen Schranke für Aufwandsfunktion angegeben. Das heißt deren Wachstumsgeschwindigkeit bzw. Größenordnung. Eine Asymptote ist eine Gerade, der sich eine Kurve bei immer größer werdender Entfernung vom Koordinatenursprung unbegrenzt nähert. Eine einfache Vergleichsfunktion ist $f(n)\in O(g(n))$ für Aufwandsfunktionen mit $g:\mathbb {N} \to \mathbb {N}$

Definition

Für eine Funktion $f:\mathbb {N} \to \mathbb {N}$ ist die Menge $O(f(n))$ wie folgt definiert:

$O(f(n))=\{g:\mathbb {N} \to \mathbb {N} |\exists c\in \mathbb {R} ^{>0},\exists n_{o}\in \mathbb {N} \ \forall n\geq n_{0}:g(n)\leq c\cdot f(n)\}$

Anschaulich formuliert bedeutet das, dass O(f(n)) die Menge aller durch f nach oben beschränkter Funktionen ist und somit die asymptotische obere Schranke ist.

Die Definition veranschaulichst sieht folgendermaßen aus:

$g(n)\in O(f(n))\Leftrightarrow \exists c>0,\exists n_{0}\forall n\geq n_{0}:g(n)\leq c\cdot f(n)$

Das heißt g wächst nicht schneller als f. Das bedeutet wiederrum ${\frac {g(n)}{f(n)}}$ ist für genügend große n durch eine Konstante c nach oben beschränkt.

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.2 zu finden.

$\Omega$ -Notation

Für eine Funktion $f:\mathbb {N} \to \mathbb {N}$ ist die Menge $\Omega (f(n))$ wie folgt definiert:

$\Omega (f(n))=\{g:\mathbb {N} \to \mathbb {N} |\exists c\in \mathbb {R} ^{>0},\exists n_{o}\in \mathbb {N} \ \forall n\geq n_{0}:g(n)\geq c\cdot f(n)\}$

Anschaulich formuliert bedeutet das, dass $\Omega (f(n))$ die Menge aller durch f nach unten beschränkter Funktionen ist und somit die asymptotische untere Schranke ist.

$\Theta$ -Notation

Die exakte Ordnung $\Theta$ von f(n) ist definiert als:

$\Theta (f(n))=\{g:\mathbb {N} \to \mathbb {N} |\exists c_{1}\in \mathbb {R} ^{>0},\exists c_{2}\in \mathbb {R} ^{>0},\exists n_{o}\in \mathbb {N} \ \forall n\geq n_{0}:c_{1}\cdot f(n)\geq g(n)\geq c_{2}\cdot f(n)\}$

Oder etwas kompakter:

$\Theta (f(n))=O(f(n))\bigcap \Omega (f(n))$

Anschaulich formuliert bedeutet das, dass $\Theta$ die Menge aller durch f nach unten und oben beschränkter Funktionen und somit die asymptotische untere und obere Schranke ist.

Beweis

Zu zeigen: $\Theta (f(n))\subseteq O(f(n))\cap \Omega (f(n))~und~\Theta (f(n))\supseteq O(f(n))\cap \Omega (f(n))$

$\Theta (f(n))\subseteq O(f(n))\cap \Omega (f(n)):$

Zeige $g(n)\in \Theta (f(n))\Rightarrow g(n)\in O(f(n))\cap \Omega (f(n)).$

• $g(n)\in \Theta (f(n))\Rightarrow \exists c_{1},c_{2},n_{0}:\forall n\geq n_{0}:c_{1}f(n)\geq g(n)\geq c_{2}f(n)$

$\Rightarrow \exists c_{1},n_{0}:\forall n\geq n_{0}:c_{1}f(n)\geq g(n)~und~\exists c_{2},n_{0}:\forall n\geq n_{0}:c_{1}f(n)\geq g(n)\geq c_{2}f(n)$

$\Rightarrow g(n)\in O(f(n))~und~g(n)\in \Omega (f(n))$

$\Rightarrow g(n)\in O(f(n))\cap \Omega (f(n))$

Beispiel 1

Wir stellen uns die Frage, ob $n^{2}\in O(n^{3})$ bzw. ob $n^{3}$ eine obere Schranke für $n^{2}$ ist. Die Antwort ist ja. Die Begründung dazu lautet folgendermaßen:

$n_{0}=1,c=1$

$\Rightarrow n^{2}\leq n^{3}$

$\Rightarrow 1\leq n\ {\text{für}}\ n\geq 1$

Beispiel 2

Wir stellen uns die Frage, ob $n^{3}\in O(n^{2})$ bzw. ob $n^{2}$ eine obere Schranke für $n^{3}$ ist. Die Antwort ist nein. Beweisen kann man das durch Widerspruch. Unsere Annahme ist: $\exists c,n_{0}\in \mathbb {N} :n^{3}\leq c\cdot n^{2},{\text{für alle }}n>n_{0}$

$n^{3}\leq c\cdot n^{2},{\text{für alle }}n>n_{0}$

$\Rightarrow n\leq c,{\text{für alle }}n>n_{0}$

Wähle $n=c+n_{0}\Rightarrow c+n_{0}\leq c$ Widerspruch!!

Lemma

Für beliebige Funktionen f,g gilt:
$O(f(n)+g(n))=O(max(f(n),g(n))$

Beweis in beide Richtungen

$t(n)\in O(f(n)+g(n))\Rightarrow t(n)\in O(max(f(n),g(n)))$

$t(n)\in O(f(n)+g(n))\Leftarrow t(n)\in O(max(f(n),g(n)))$

Als erstes machen wir den Beweis nach rechts ($\Rightarrow$)

$\exists c,n_{0}\in \mathbb {N} :t(n)\leq c\cdot (f(n)+g(n))\ \forall n>n_{o}$

$\Rightarrow t(n)\leq 2\cdot c\cdot max(f(n),g(n))\ \forall n>n_{0}$

$\Rightarrow t(n)\in O(max(f(n)),g(n)))$

nun der Beweis nach links ($\Leftarrow$)

$\exists c,n_{0}\in \mathbb {N} :t(n)\leq c\cdot (max(f(n),g(n)))\ \forall n>n_{0}$

$\Rightarrow t(n)\leq c\cdot (f(n)+g(n))\ \forall n>n_{0}$

$\Rightarrow t(n)\in O(f(n),g(n))$

Beispiel

$O(n^{4}+n^{2})=O(n^{4})$

$O(n^{4}+4\cdot n^{3})=O(n^{4})$

$O(n^{4}+2^{n})=O(2^{n})$

Lemma

1. $O(f(n))\subseteq O(g(n))\ {\text{genau dann wenn }}f(n)\in O(g(n))$
2. $O(f(n))=O(g(n))\ {\text{genau dann wenn }}f(n)\in O(g(n))\land g(n)\in O(f(n))$
3. $O(f(n))\subset O(g(n))\ {\text{genau dann wenn }}f(n)\in O(g(n))\land g(n)\notin O(f(n))$

Beweis in beide Richtungen

Beweis zu 1. nach rechts ($\Rightarrow$)

$O(f(n))\subseteq O(g(n))\Rightarrow f(n)\in O(g(n))$

$f(n)\in O(f(n))\subseteq O(g(n))\Rightarrow f(n)\in O(g(n))$

Beweis zu 1. nach links ($\Leftarrow$)

$O(f(n))\subseteq O(g(n))\Leftarrow f(n)\in O(g(n))$

$f(n)\in O(g(n))\Rightarrow \exists c_{0},n_{0}\in \mathbb {N} :f(n)\leq c_{0}\cdot g(n)\ \forall n>n_{0}$ (siehe Definition)

und sei t(n) ein beliebiges Element der Menge O(f(n))

$t(n)\in O(f(n))\Rightarrow \exists c_{1},n_{1}\in \mathbb {N} :t(n)\leq c_{1}\cdot f(n)\ \forall n>n_{1}$ (siehe Definition)

$\Rightarrow t(n)\leq c_{1}\cdot f(n)\leq c_{1}\cdot c_{0}\cdot g(n)\ \forall n>max(n_{0},n_{1})$

$t(n)\in O(f(n))\Rightarrow t(n)\in O(g(n))$

$O(f(n))\subseteq O(g(n))$ (Definition der Teilmenge, da t(n) ein beliebiges Element ist)

Beispiele

$O(n^{2})=\{n^{2},2n^{2}-6,3n^{2}+5,{\frac {1}{2}}n^{2}+8,...\}$

Damit ist

$(3n^{2}+5)\in O(n^{2})$

$O(3n^{2}+5)\subseteq O(n^{2})$

$O(3n^{2}+5)=\{n^{2},2n^{2}-6,3n^{2}+5,{\frac {1}{2}}n^{2}+8,...\}$

Damit ist

$n^{2}\in O(3n^{2}+5)$

$O(n^{2})\subseteq O(3n^{2}+5)$

Damit ist

$O(n^{2})=O(3n^{2}+5)$

Lemma

Falls $f(n)\in O(g(n))~und~g(n)\in O(h(n))$, dann ist auch $f(n)\in O(h(n))$. 

Beweis

$f(n)\leq c_{0}\cdot g(n)\ \forall n>n_{0}~und$

$g(n)\leq c_{1}\cdot h(n)\ \forall n>n_{1}~und$

$\Rightarrow f(n)\leq c_{0}\cdot g(n)\leq c_{0}\cdot c_{1}\cdot h(n)\ \forall n\geq max(n_{0},n_{1})$

Dabei ist $c_{0}\cdot c_{1}$ eine Konstante.

Beispiel

$O(n^{2})=O(3n^{2})=O({\frac {1}{2}}n^{2})$

$O(n^{2})\subseteq O(3n^{2})\subseteq O({\frac {1}{2}}n^{2})$

$O(n^{2})\subseteq O(n^{2,5})\subseteq O(n^{3})$

$O(n^{2})\subset O(n^{2,5})\subset O(n^{3})$

Lemma

1. $lim_{n\to \infty }(f(n)/g(n))=c,c>0\Rightarrow O(f(n))=O(g(n))$
2. $lim_{n\to \infty }(f(n)/g(n))=0\Rightarrow O(f(n))\subset O(g(n))$

Ein häufiges Problem sind Grenzwerte der Art ${\frac {\infty }{\infty }}$ oder ${\frac {0}{0}}$ Bei diesem Problem kann man als Ansatz die Regel von de l'Hospital verwenden.

Satz(Regel von de L'Hospital) $x\to \infty$
Seien f und g auf dem Intervall $[\alpha ,\infty )$ differenzierbar.
Es gelte $lim_{x\to \infty }f(x)=lim_{x\to \infty }g(x)=0(bzw.=\infty )$ 
und es existiere $lim_{x\to \infty }{\frac {f'(x)}{g'(x)}}$.
Dann existiert auch $lim_{x\to \infty }{\frac {f(x)}{g(x)}}$ und es gilt:
$lim_{x\to \infty }{\frac {f'(x)}{g'(x)}}=lim_{x\to \infty }{\frac {f(x)}{g(x)}}$

Beispiel

1. $f(n)=3n+5,g(n)=n$

$lim_{n\to \infty }{\frac {3n+5}{n}}\Rightarrow lim_{n\to \infty }{\frac {3}{1}}=3>0\Rightarrow O(3n+5)=O(n)$

2. $f(n)=n^{2}+5,g(n)=n^{3}$

$lim_{n\to \infty }{\frac {n^{2}+5}{n^{3}}}\Rightarrow lim_{n\to \infty }{\frac {2n}{3n^{2}}}\Rightarrow lim_{n\to \infty }{\frac {2}{6n}}=0\Rightarrow O(n^{2}+5)\subset O(n^{3})$

Beim zweiten Beispiel musste die Regel von de l'Hospital wiederholt angewandt werden.

Lemma

Gibt es immer eine Ordnung zwischen den Funktionen? Es gibt Funktionen f und g mit $f(n)\notin O(g(n))~und~g(n)\notin O(f(n))$. Ein Beispiel sind die Funktionen sin(n) und cos(n).

Für alle $m\in \mathbb {N} ~gilt:O(n^{m})\subseteq O(n^{m+1})$

Beweis durch Widerspruch

Wir nehmen an, dass $s(n)\in O(n^{k})$,

das heißt $\exists c,n_{0},\forall n>n_{0}:s(n)\leq c\cdot n^{k}$.

Aber es muss auch $s(n)\notin O(n^{k+1})$ gelten,

das heißt $\exists n>n_{0}:s(n)>c\cdot n^{k+1}$

$\Rightarrow \exists n>n_{0}:und~n<1$

Komplexitätsklassen

Auf dieser Seite werden die Komplexitätsklassen behandelt.

Wir sagen sei $f(n)=a_{m}\cdot n^{m}+a_{m-1}\cdot n^{m-1}+...+a_{1}\cdot n+a_{0},~wobei~a_{i}\in \mathbb {R} ^{+}{\text{für}}~0\leq i\leq m.~Dann~gilt~f(n)\in O(n^{m}).$ Und wir sagen, ein Algorithmus mit Komplexität f(n) benötigt höchstens polynomielle Rechenzeit, falls es ein Polynom p(n) gibt, mit $f(n)\in O(p(n))$. Des weiteren sagen wir, dass ein Algorithmus höchstens exponentielle Rechenzeit benötigt, falls es eine Konstante $a\in \mathbb {R} ^{+}$ gibt, mit $f(n)\in O(a^{n})$.

Die Komplexitätsklassen sind:

$O(1)$	der konstante Aufwand, das bedeutet der Aufwand ist nicht abhängig von der Eingabe
$O(log~n)$	der logarithmische Aufwand
$O(n)$	der lineare Aufwand
$O(n\cdot log~n)$
$O(n^{2})$	der quadratische Aufwand
$O(n^{k})\ {\text{für}}\ k\geq 0$	der polynomiale Aufwand
$O(2^{n})$	der exponentielle Aufwand

Wachstum

f(n)	n=2	$2^{4}=16$	$2^{8}=256$	$2^{10}=1024$	$2^{20}=1048576$
ldn	1	4	8	10	20
n	2	16	256	1024	1048576
$n\cdot ldn$	2	64	2048	10240	20971520
$n^{2}$	4	256	65536	1048576	$\approx 10^{12}$
$n^{3}$	8	4096	16777200	$\approx 10^{9}$	$\approx 10^{18}$
$2^{n}$	4	65536	$\approx 10^{77}$	$\approx 10^{308}$	$\approx 10^{315653}$

Zeitaufwand

Nun stellen wir uns die Frage, wie groß bezüglich der Rechenschritte darf, oder kann ein Problem sein, je nach Komplexitätsklasse, wenn die Zeit T begrenzt ist? Wir nehmen an, dass wir pro Schritt eine Rechenzeit von $1\mu s=(10^{-6}s)$ brauchen. In der folgenden Tabelle steht T für die Zeitbegrenzung und G für die maximale Problemgröße.

G	T=1Min.	1 Std.	1 Tag	1 Woche	1 Jahr
n	$6\cdot 10^{7}$	$3,6\cdot 10^{9}$	$8,6\cdot 10^{10}$	$6\cdot 10^{11}$	$3\cdot 10^{13}$
$n^{2}$	7750	$6\cdot 10^{4}$	$2,9\cdot 10^{5}$	$7,8\cdot 10^{5}$	$5,6\cdot 10^{6}$
$n^{3}$	391	1530	4420	8450	31600
$2^{n}$	25	31	36	39	44

Ein Beispiel ist für T=1 Min. : $1000\cdot 1000\cdot 60=6\cdot 10^{7}\mu s~(10^{7}~Schritte)$

Typische Problemklassen

Aufwand	Problemklasse
$O(1)$	für einige Suchverfahren für Tabellen (Hashing)
$O(log~n)$	für allgemeine Suchverfahren für Tabellen (Baum-Suchverfahren)
$O(n)$	für sequenzielle Suche, Suche in Texten, syntaktische Analyse von Programmen (bei "guter" Grammatik)
$O(n\cdot log~n)$	für Sortieren
$O(n^{2})$	für einige dynamische Optimierungsverfahren (z.B. optimale Suchbäume), einfache Multiplikation von Matrix-Vektor
$O(n^{3})$	für einfache Matrizen Multiplikationen
$O(2^{n})$	für viele Optimierungsprobleme (z.B. optimale Schaltwerke), automatisches Beweisen (im Prädikatenkalkül 1.Stufe)

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.3 zu finden.

Aufwandsanalyse von iterativen Algorithmen

Auf dieser Seite wird der Aufwand von iterativen Algorithmen analysiert. Als Aufwand wird die Anzahl der durchlaufenen Operationen zur Lösung des Problems bezeichnet ( Zuweisungen, Vergleiche...). Häufig ist der Aufwand abhängig vom Eingabeparameter (Problemgröße). Die Aufwandsklasse sagt, wie der Aufwand in Abhängigkeit von der Problemgröße wächst. Doch wie kann man nun bei beliebigem Java Code die Aufwandsklasse bestimmen?

Aufwand von Programmen ablesen

void alg1(int n){
     int m = 2;
     int i;
     int k = n;
     while (n > 0){
         i = k;
         while (i > 0) {
               m = m + i;
               i = i / 2;
         }
         n = n - 1;
    }
}

Die Aufwandsklasse ist $O(n\cdot log~n)$. Die äußere Schleife wird n-mal durchlaufen und die Innere Schleife log n-mal.

void alg1(int n) {
      int m = 1;
      int i = 0;
      while (m < n) {
         while (i < m) 
              i = i + 1;
      m = m + i;
      }
}

Hier ist die Aufwandsklasse O(n+log n). In jedem Durchlauf der äußeren Schleife wird m verdoppelt, d.h. sie läuft log n Mal. Die innere Schleife läuft bis n/2, aber nicht jedes Mal, weil i nur ein Mal auf 0 gesetzt wird. Man könnte als Aufwandsklasse auch O(n) sagen, da der Summand log n nicht ins Gewicht fällt.

Bestandteile iterativer Algorithmen

Zum einen haben wir elementare Anweisungen wie Zuweisungen und Vergleiche. Diese haben einen Aufwand von 1.

Des Weiteren haben wir Sequenzen $\alpha _{1}~und~\alpha _{2}$ oder auch $\alpha _{1};\alpha _{2}$ geschrieben. Die obere Grenze ist $O(f_{\alpha _{1}}(n))+O(f_{\alpha _{2}}(n))$ und die untere Grenze ist $\Omega (f_{\alpha _{1}}(n))+\Omega (f_{\alpha _{2}}(n))$. Dabei ist $f_{\alpha _{1}}(n)$ der Aufwand, der bei der Ausführung von $\alpha _{1}$ entsteht.

Ein weiterer Bestandteil ist die Selektion. $if(B)\{\alpha _{1}\}else\{\alpha _{2}\}$. Hier ist die obere Grenze $O(f_{B}(n))+O(max(f_{\alpha _{1}}(n),f_{\alpha _{2}}(n)))$ und die untere Grenze $\Omega (f_{B}(n))+\Omega (min(f_{\alpha _{1}}(n),f_{\alpha _{2}}(n)))$.

Außerdem haben wir Iterationen $while(B)\{\alpha \}$. Hierbei ist die obere und die untere Grenze die Anzahl der Schleifendurchläufe, $(O(f_{B}(n))+O(f_{\alpha }(n)))$ und die untere Grenze $(\Omega (f_{B}(n))+\Omega (f_{\alpha }(n)))$. Doch wie ist der Aufwand für eine for-Schleife? Ein Beispiel ist $for(\alpha _{1};B;\alpha _{2})\{\alpha _{3}\}$. Die Antwort ist die Abbildung auf eine while-Schleife.

$\alpha _{1};$

while(B) {

     $\alpha _{3};$

     $\alpha _{2};$

}

Beispiel Sequenz

public int berechne(int n) {
  int x = 0;
  x = x + 1;
  return x;
}

Jede Zeile hat den Aufwand $\Theta (1)$. Wie viele Operationen werden nun durchlaufen? Und ist die Anzahl abhängig vom Eingabeparameter? Der Aufwand ist $f(n)=\Theta (1)+\Theta (1)+\Theta (1)=3\cdot \Theta (1)$

Die Aufwandsklasse ist somit $\Theta (f(n))=\Theta (1)$

Beispiel Schleifen

public int berechne(int n) {
  int x = 0;
  for (int i=0; i < n; i++) {
    x = x + 1;
  }
  return x;
}

Die for Schleife hat den Aufwand $n\cdot \Theta (1)$. Die Initialisierung und das return haben jeweils den Aufwand $\Theta (1)$.

Der Gesamtaufwand ist somit $f(n)=\Theta (1)+n\cdot \Theta (1)+\Theta (1)=2\cdot \Theta (1)+\Theta (n)$. Somit ist die Aufwandsklasse $\Theta (f(n))=\Theta (n)$.

public int berechne(int n) {
  int x = 0;
  for (int i=0; i < n; i++) {
    for (int j=0; j < n; j++) {
      x = x + 1;
    }
  }
  return x;
}

Hier hat die for-Schleife den Aufwand $n\cdot (n\cdot \Theta (1))$ und die Initialisierung und das return wieder $\Theta (1)$. Damit ergibt der sich Gesamtaufwand $f(n)=\Theta (1)+n^{2}\cdot \Theta (1)+\Theta (1)=2\cdot \Theta (1)+\Theta (n^{2})$. Daraus folgt die Aufwandsklasse $\Theta (f(n))=\Theta (n^{2})$.

Beispiel Selektion

public int berechne(int n) {

   if (n % 2 == 0) {

      int x = 0;
      for (int i=0; i < n; i++) {

         x = x + 1;

      }
      return x;
   }else{
      return n;
   }
}


Hier hat die for-Schleife einen Aufwand von $\Theta (n)$. Die Initialisierung und das return wieder $\Theta (1)$.

Die obere Grenze ist somit $O(f(n))=\Theta (1)+O(max(\Theta (n),\Theta (1))=O(n)$ und die untere Grenze $\Omega (f(n))=\Theta (1)+\Omega (min(\Theta (n),\Theta (1))=\Omega (1)$

Faustregeln

Zu den häufig verwendeten Faustregeln gehört, dass wenn wir keine Schleife haben, der Aufwand konstant ist. Eine weitere ist, dass bei einer Schleife immer ein linearer Aufwand vorliegt. Bei zwei geschachtelten Schleifen haben wir immer einen quadratischen Aufwand. Doch die Faustegeln gelten nicht ohne Ausnahmen. Besonders Acht geben muss man bei Aufwandsbestimmungen für Schleifen, bei mehreren Eingabevariablen, bei Funktionsaufrufen und bei Rekursionen.

Aufwandsbestimmung für Schleifen

public int berechne(int n) {

  int x = 0;

  for (int i=0; i < 5; i++) {

    x = x + 1;

  }

  return x;

}


Der Schleifenabbruch hängt nicht vom Eingabeparameter ab. Der Aufwand beträgt $f(n)=\Theta (1)+5\cdot \Theta (1)+\Theta (1)=7\cdot \Theta (1)$ somit haben wir die Aufwandsklasse $\Theta (fn))=\Theta (1)$

public int berechne(int n) {

  int x = 0;

  for (int i=1; i < n; i = 2*i) {

    x = x + 1;

  }

  return x;

}


Hier wächst die Laufvariable nicht linear an.Daher ist der Aufwand $f(n)=\Theta (1)+log_{2}n\cdot \Theta (1)+\Theta (1)$ und wir haben die Aufwandsklasse $\Theta (f(n))=\Theta (log~n)$.

Doch gibt es eine allgemeine Methodik zum Bestimmen des Schleifenaufwands?

for (int i=1; i < n; i=2*i) {

  x = x + 1;
}


Schritt 1: Wie entwickelt sich hier die Laufvariable? Der Startwert i ist 1 und die Veränderung in jedem Schritt ist $i=2\cdot i$. Die Laufvariable entwickelt sich somit wie folgt:

Nach dem 1. Durchlauf $i=1\cdot 2=2^{1}$

Nach dem 2. Durchlauf $i=(1\cdot 2)\cdot 2=2^{2}$

Nach dem 3. Durchlauf $i=((1\cdot 2)\cdot 2)\cdot 2=2^{3}$

Nach dem k. Durchlauf $i=2^{k}$

Schritt 2: Nach wie vielen Durchläufen wird die Schleife abgebrochen?

Der Abbruch erfolgt, wenn $i\geq n$

     :$i\geq n\ \ \ \ \ \ \ |i=2^{k}$

$\Leftrightarrow 2^{k}\geq n\ \ \ \ \ |log_{2}$

$\Leftrightarrow k\geq log_{2}n$

Somit erfolgt ein Abbruch nach $k=$ ⌈ $log_{2}n$ ⌉ Durchläufen.

public int berechne(int[] f1, int[] f2) {

   int result = 0;

   for (int i=0; i < f1.length; i++) {

      for (int j=0; j < f2.length; j++) {

         if (f1[i] == f2[j]) result++;

      }

   }

   return result;

}


Hier haben wir nun eine for Schleife mit mehreren Eingabevariablen. Die Problemgrößen sind $n=f1.length~und~m=f2.length$.

public int berechne2(int[] f1, int[] f2){

   f2 = mergeSort(f2);
   int result = 0;

   for (int i=0; i < f1.length; i++) {
      if (binarySearch(f2, f1[i])) result++;

   }

   return result;
}


Der Aufwand ist hier $f(n,m)=\Theta (m\cdot log~m)+\Theta (1)+n\cdot (\Theta (log~m)+O(1))+\Theta (1)$. Somit ist die Aufwandsklasse $\Theta (f(n,m))=\Theta (m\cdot log~m+n\cdot log~m)$.

In diesem Beispiel haben wir wieder mehreren Eingabevariablen. Diese sind die gleichen Problemgrößen $n=f1.length~und~m=f2.length$.

public int berechne2(int[] f1, int[] f2){

   int result = 0;

   for (int i=0; i < f1.length; i++) {
      for (int j=0; j < f2.length; j++) {
         if (f1[i] == f2[j]) result++;

      }
   }

   return result;
}


Der Aufwand ist hier wie folgt: $f(n,m)=\Theta (1)+n\cdot (m\cdot (\Theta (1)+O(1)))+\Theta (1)$. Somit ist die Aufwandsklasse $\Theta (f(n,m))=\Theta (n\cdot m)$.

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.4 zu finden.

Aufwandsanalyse von rekursiven Algorithmen

Auf dieser Seite wird der Aufwand von rekursiven Algorithmen untersucht.

public int fib(int n) {

   if (n == 0 || n == 1) {
      return 1;
   } else {
      return fib(n-1) + fib(n-2);
   }
}


Wie ist nun der Aufwand für Fibonacci? Bei Rekursionsabbruch $f(n)=\Theta (1)+\Theta (1)$ und im Rekursionsfall $f(n)=\Theta (1)+???$. Zur Bestimmung benutzen wir Rekursionsgleichungen.

Rekursionsgleichungen

Eine Rekursionsgleichung ist eine Gleichung oder Ungleichung, die eine Funktion anhand ihrer Anwendung auf kleinere Werte beschreibt.

Rekursionsgleichung für Fibonacci:

$T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n=0\lor n=1)\\\Theta (1)+T(n-1)+T(n-2)&sonst\end{array}}\right.$

Lösung von Rekursionsgleichungen

Die Frage ist nun, welche Aufwandklasse T(n) beschreibt. Dies könnten alle möglichen Aufwandsklassen sein. Methoden um dieses Problem zu lösen, sind die vollständige Induktion und das Master-Theorem.

Spezialfall Divide and Conquer Algorithmus

Ein Divide-and-Conquer Algorithmus stellt im Allgemeinen eine einfache, rekursive Version eines Algorithmus dar und hat drei Schritte:

1. Divide: Unterteile das Problem in eine Zahl von Teilproblemen
2. Conquer: Löse das Teilproblem rekursiv. Wenn das

Teilproblem klein genug ist, dann löse das Teilproblem direkt (z.B. bei leeren oder einelementigen Listen)

1. Combine: Die Lösungen der Teilprobleme werden zu einer Gesamtlösung kombiniert.

Merge Sort ist beispielsweise ein Divide and Conquer Algorithmus.

1. Divide: Zerteile eine Folge mit n Elementen in zwei Folgen mit je n/2 Elementen.
2. Conquer: Wenn die resultierende Folge 1 oder 0 Elemente enthält, dann ist sie sortiert.Ansonsten wende Merge Sort rekursiv an.
3. Combine: Mische die zwei sortierten Teilfolgen.

public List mergeSort(List f) {
  if (f.size() <= 1) {
    return f;
  } else {
    int m = f.size() / 2;
    List left = mergeSort(f.subList(0,m));
    List right = mergeSort(f.subList(m,f.size());
    return merge(left, right);
  }
}

Die dazugehörige Rekursionsgleichung lautet:

$T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n\leq 1)\\\Theta (1)+2\cdot T(n/2)+\Theta (n)&sonst\end{array}}\right.$

Im Allgemeinen ist die Rekursionsgleichung für Divide and Conquer Algorithmen:

$T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n\leq 1)\\D(n)+a\cdot T(n/b)+C(n)&sonst\end{array}}\right.$

mit D(n) als Aufwand für Divide, T(n/b) als Aufwand für Conquer und C(n) als Aufwand für Combine.

Ab- und Aufrunden

Die Rekursionsgleichung von MergeSort beschreibt den Aufwand für den schlechtesten Fall.

$T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n\leq 1)\\\Theta (1)+T(n/2)+T(n/2)+\Theta (n)&sonst\end{array}}\right.$

Aber die Annahme, dass n eine geeignete ganze Zahl ist ergibt normalerweise das gleiche Ergebnis wie eine beliebige Zahl mit Auf- bzw. Abrunden. Dies führt zur einfacheren Rekursionsgleichung:

$T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n\leq 1)\\\Theta (1)+2\cdot T(n/2)+\Theta (n)&sonst\end{array}}\right.$

Beispiel Binäre Suche

public List binarySearch(ArrayList<Integer> f, int e) {
  if (f.size() == 0) {
    return -1;
  } else {
    int m = f.size() / 2;
    if (f.get(m) == e) {
      return m;
    } else if (f.get(m) < e) {
      return binarySearch(f.subList(0, m), e);
    } else {
      return binarySearch(f.subList(m+1, f.size()), e);
    }
  }
}

Die Rekursionsgleichung lautet $T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n=0)\\\Theta (1)+T(n/2)&sonst\end{array}}\right.$

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.4 zu finden.

Vollständige Induktion

Auf dieser Seite wird die vollständige Induktion behandelt. Es handelt sich hierbei um eine rekursive Beweistechnik aus der Mathematik. Sie ist gut geeignet, um Eigenschaften von rekursiv definierten Funktionen zu beweisen.

Vorgehen

Zunächst vermutet man eine Eigenschaft (z.B. Aufwandsklasse einer Rekursionsgleichung). Nun folgt der Induktionsanfang: Eigenschaft hält für ein kleines n. Als nächstes folgt der Induktionsschritt: Die Annahme ist, dass wir es bereits für ein kleineres n gezeigt haben und wenn die Eigenschaft für kleinere n hält, dann hält sie auch für das nächstgrößere n!

Beispiel 1

$T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für}}\ n\leq 1\\4\cdot T({\frac {n}{2}})+\Theta (n^{3})&sonst\end{array}}\right.$

Nun wollen wir die obere Grenze für den Aufwand bestimmen. Unsere Vermutung ist, dass $T(n)\in O(n^{3})$. Nun müssen wir zeigen, dass $\exists n_{0},c:\forall n\geq n_{o}:T(n)\leq c\cdot n^{3}$ ( siehe Definition der O-Notation). Die vereinfachte Annahme lautet $n=2^{k}$. Hierbei werden keine Spezialfälle behandelt und im Induktionsschritt wird von ${\frac {n}{2}}$ nach n gegangen.

Induktionsvermutung: $T({\frac {n}{2}})\leq c\cdot ({\frac {n}{2}})^{3}$

Induktionsschritt: Wir beweisen von ${\frac {n}{2}}~nach~n$

zu zeigende obere Grenze:

$T(n)\leq c\cdot n^{3}\ \ \ |T(n)=4\cdot T({\frac {n}{2}})+n^{3}$

Rekursionsgleichung einsetzen:

$\Leftrightarrow 4\cdot T({\frac {n}{2}})+n^{3}\leq c\cdot n^{3}|T({\frac {n}{2}})\leq c\cdot ({\frac {n}{2}})^{3}$

Induktionsvermutung einsetzen:

$\ \Leftarrow 4\cdot c\cdot ({\frac {n}{2}})^{3}+n^{3}\leq c\cdot n^{3}$

$\ \Leftrightarrow 4\cdot c\cdot ({\frac {n^{3}}{8}})+n^{3}\leq c\cdot n^{3}|-c\cdot n^{3}$

$\ \Leftrightarrow -{\frac {1}{2}}\cdot c\cdot n^{3}+n^{3}\leq 0|:n^{3}$

$\ \Leftrightarrow -{\frac {1}{2}}\cdot c+1\leq 0|+{\frac {1}{2}}\cdot c$

$\ \Leftrightarrow 1\leq {\frac {1}{2}}\cdot c|\cdot 2$

$\ \Leftrightarrow 2\leq c$

Somit ist der Induktionsschritt erfolgreich, wenn $c\geq 2$.

Induktionsanfang

Wir zeigen die Induktionsvermutung für einen Anfangswert, am einfachsten ist es, dies für den Rekursionsabbruch zu zeigen.

Zu zeigende obere Grenze:

$T(1)\leq c\cdot 1^{3}|T(1)=1$

Rekursionsgleichung einsetzen:

$\Leftrightarrow 1\leq c$

Der Induktionsanfang ist erfolgreich, wenn $c\geq 1$ ist. Doch wann können wir zeigen, dass $T(n)\leq c\cdot n^{3}$ ist? Für den Wert, den wir im Induktionsanfang gezeigt haben, also für $n_{0}=1$ und wenn $(c\geq 2\land c\geq 1)\Rightarrow c\geq 2$.

Beispiel 2

$T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für}}\ n\leq 1\\4\cdot T({\frac {n}{2}})+\Theta (n)&sonst\end{array}}\right.$

Nun wollen wir die obere Grenze für den Aufwand bestimmen. Unsere Vermutung ist, dass $T(n)\in O(n^{2})$. Nun müssen wir zeigen, dass $\exists n_{0},c:\forall n\geq n_{0}:T(n)\leq c\cdot n^{2}$. Die vereinfachte Annahme lautet $n=2^{k}$.

Induktionsvermutung: $T({\frac {n}{2}})\leq c\cdot ({\frac {n}{2}})^{2}$

Induktionsschritt: Wir beweisen von ${\frac {n}{2}}~nach~n$

$T(n)\leq c\cdot n^{2}|T(n)=4\cdot T({\frac {n}{2}})+n$

$\Leftrightarrow 4\cdot T({\frac {n}{2}})+n\leq c\cdot n^{2}|T({\frac {n}{2}})\leq c\cdot ({\frac {n}{2}})^{2}$

$\Leftarrow 4\cdot c\cdot ({\frac {n}{2}})^{2}+n\leq c\cdot n^{2}$

$\Leftrightarrow 4\cdot c\cdot ({\frac {n^{2}}{4}})+n\leq c\cdot n^{2}|-c\cdot n^{2}$

$\Leftrightarrow n\leq 0$

Das Problem ist nun, dass wir den Induktionsschritt für positive n zeigen wollen und nicht für negative, daher müssen wir neu ansetzen.

Induktionsvermutung:

Dabei gibt es folgenden Trick: Modifiziere die Induktionsvermutung, in dem ein kleineres Polynom addiert wird.

$T({\frac {n}{2}})\leq c_{1}\cdot ({\frac {n}{2}})^{2}+c_{2}\cdot {\frac {n}{2}}$

Induktionsschritt: Wir beweisen von ${\frac {n}{2}}~nach~n$

$T(n)\leq c_{1}\cdot n^{2}+c_{2}\cdot n$

$\Leftrightarrow 4\cdot T({\frac {n}{2}})+n\leq c_{1}\cdot n^{2}+c_{2}\cdot n$

$\Leftarrow 4\cdot (c_{1}\cdot ({\frac {n}{2}})^{2}+c_{2}\cdot {\frac {n}{2}})+n\leq c_{1}\cdot n^{2}+c_{2}\cdot n$

$\Leftrightarrow c_{1}\cdot n^{2}+2\cdot c_{2}\cdot n+n\leq c_{1}\cdot n^{2}+c_{2}\cdot n|-c_{1}\cdot n^{2};-c_{2}\cdot n$

$\Leftrightarrow c_{2}\cdot n+n\leq 0$

$\Leftrightarrow c_{2}+1\leq 0$

$\Leftrightarrow c_{2}\leq -1$

Induktionsanfang für n=1

$T(1)\leq c_{1}\cdot 1^{2}+c_{2}\cdot 1|T(1)=1$

$\Leftrightarrow 1\leq c_{1}+c_{2}|-c_{2}$

$\Leftrightarrow 1-c_{2}\leq c_{1}$

Wann können wir nun zeigen, dass $T(n)\leq c_{1}\cdot n^{2}+c_{2}\cdot n$?

Für $n_{0}=1~und~wenn~(c_{2}\leq -1\land c_{1}\geq 1-c_{2})$. Somit haben wir gezeigt, dass $T(n)\in O(n^{2}+n)\Rightarrow T(n)\in O(max(n^{2},n))\Rightarrow T(n)\in O(n^{2})$

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.2.5 zu finden.

Mastertheorem

Auf dieser Seite wird das Master Theorem behandelt. Die Mastermethode ist ein „Kochrezept“ zur Lösung von Rekursionsgleichungen der Form:

$T(n)=aT(n/b)+f(n)$ mit den Konstanten $a\geq 1~und~b>1$, f(n) ist eine asymptotische, positive Funktion, d.h. $f(n)>0\forall n>n_{0}$

• a steht dabei für die Anzahl der Unterprobleme.

• n/b ist die Größe eines Unterproblems

• T(n/b) ist der Aufwand zum Lösen eines Unterproblems (der Größe n/b)

• f(n) ist der Aufwand für das Zerlegen und Kombinieren in bzw. von Unterproblemen

Bei der Mastermethode handelt es sich um ein schnelles Lösungsverfahren zur Bestimmung der Laufzeitklasse einer gegebenen rekursiv definierten Funktion. Dabei gibt es 3 gängige Fälle:

• Fall 1: Obere Abschätzung
• Fall 2: Exakte Abschätzung
• Fall 3: Untere Abschätzung

Lässt sich keiner dieser 3 Fälle anwenden, so muss die Komplexität anderweitig bestimmt werden und wir müssen Voraussetzungen für die Anwendung des Mastertheorems überprüfen.

Dafür vergleicht man $f(n)$ mit $n^{log_{b}a}$. Wir verstehen n/b als $\llcorner n/b\lrcorner ~oder~\ulcorner n/b\urcorner$. Im Folgenden verwenden wir die verkürzte Notation $log_{2}n~als~ld~n$.

Fall 1

Wenn $f(n)\in O(n^{log_{b}a-\epsilon }){\text{für ein }}\epsilon >0$. Daraus folgt, dass f(n) polynomiell langsamer wächst als $n^{log_{b}a}$ um einen Faktor $n^{\epsilon }$. Damit haben wir die Lösung $T(n)=\Theta (n^{log_{b}a})$.

Fall 2

Wenn $f(n)\in \Theta (n^{log_{b}a}\cdot ld^{k}n){\text{für ein }}k\geq 0$. Daraus folgt, dass f(n) und $n^{log_{b}a}\cdot ld^{k}n$ vergleichbar schnell wachsen. Damit haben wir die Lösung $T(n)=\Theta (n^{log_{b}a}\cdot ld^{k+1}n)$.

Fall 3

Wenn $f(n)\in \Omega (n^{log_{b}a+\epsilon }){\text{für ein }}\epsilon >0$ und die Regularitätsbedingung $a\cdot f(n/b)\leq c\cdot f(n)$ für eine Konstante $c\in (0,1)$ und genügend große n erfüllt. Daraus folgt, dass f(n) polynomiell schneller wächst als $n^{log_{b}a}$ um einen Faktor $n^{\epsilon }$ und f(n) erfüllt die sogenannte Regularitätsbedingung. Damit haben wir die Lösung $T(n)\in \Theta (f(n))$.

Bedeutung

In jedem Fall vergleichen wir f(n) mit $n^{lob_{b}a}$. Intuitiv kann man sagen, dass die Lösung durch die größere Funktion bestimmt wird. Im zweiten Fall wachsen sie ungefähr gleich schnell. Im ersten und dritten Fall muss f(n) nicht nur kleiner oder größer als $n^{lob_{b}a}$ sein, sondern auch polynomiell kleiner oder größer um einen Faktor $n^{\epsilon }$. Der dritte Fall kann nur angewandt werden, wenn die Regularitätsbedingung erfüllt ist.

Regularitätsbedingung

Doch wozu wird die Regularitätsbedingung benötigt? Zur Erinnerung, im dritten Fall dominiert f(n) das Wachstum von T(n). Wir müssen an dieser Stelle sicherstellen, dass auch bei rekursivem Anwenden, also wenn die Argumente kleiner werden, T(n) von f(n) dominiert wird. Veranschaulicht heißt das:

$T(n)=aT(n/b)+f(n)$

$=a(aT(n/b^{2})+f(n/b))+f(n)$

$=a^{2}T(n/b^{2})+af(n/b)+f(n)$

für $af(n/b)\leq cf(n)(c\in (0,1))$ Das Wachstum muss durch f(n) dominiert werden und darf f(n) nicht dominieren.

Die Regularitätsbedingung gilt wenn sie für f(n) und g(n) gilt auch für $f(n)\cdot g(n)$ und auch für $f(n)+g(n)$

Nachweis für $f(n)\cdot g(n)$

Voraussetzung ist, dass die Regularitätsbedingung für f(n) und g(n) gilt, d.h.:

$\exists c_{1}\in (0,1),\exists n_{1}\in \mathbb {N} ~\forall n\geq n_{1}:af(n/b)\leq c_{1}f(n)$

$\exists c_{2}\in (0,1),\exists n_{2}\in \mathbb {N} ~\forall n\geq n_{2}:ag(n/b)\leq c_{2}g(n)$

Für $(f\cdot g)(n)$ gilt:

$a(f\cdot g)(n/b)=af(n/b)\cdot ag(n/b)$

man wählt $c=c_{1}\cdot c_{2}\in (0,1)$

und $n_{0}=max~\{n_{1},n_{2}\}$

$\forall n\geq n_{0}:af(n/b)\cdot ag(n/b)\leq c_{1}f(n)\cdot c_{2}g(n)=c(f\cdot g)(n)$

Nachweis für $f(n)+g(n)$

Voraussetzung ist, dass die Regularitätsbedingung für f(n) und g(n) gilt, d.h.:

$\exists c_{1}\in (0,1),\exists n_{1}\in \mathbb {N} ~\forall n\geq n_{1}:af(n/b)\leq c_{1}f(n)$

$\exists c_{2}\in (0,1),\exists n_{2}\in \mathbb {N} ~\forall n\geq n_{2}:ag(n/b)\leq c_{2}g(n)$

Für $(f+g)(n)$ gilt:

$a(f+g)(n/b)=af(n/b)+ag(n/b)$

man wählt $c=max~\{c_{1},c_{2}\}$

und $n_{0}=max~\{n_{1},n_{2}\}$

$\forall n\geq n_{0}:af(n/b)+ag(n/b)\leq c_{1}f(n)+c_{2}g(n)\leq c(f+g)(n)$

Überblick

Ist T(n) eine rekursiv definierte Funktion der Form

$T(n)=aT(n/b)+f(n)~mit~a\geq 1,b>1,\forall n>n_{0}:f(n)>0$

Dann gilt:

• 1. Fall: Wenn $f(n)\in O(n^{log_{b}a-\epsilon })~{\text{für ein }}\epsilon >0~dann~T(n)=\Theta (n^{log_{b}a})$
• 2. Fall: Wenn $f(n)\in \Theta (n^{log_{b}a}\cdot ld^{k}n)~{\text{für ein }}k\geq 0~dann~T(n)=\Theta (n^{log_{b}a}\cdot ld^{k+1}n)$
• 3. Fall: Wenn $f(n)\in \Omega (n^{log_{b}a+\epsilon })\ {\text{für ein}}\ \epsilon >0$ und $a\cdot f(n/b)\leq c\cdot f(n)\ {\text{für eine Konstante }}c\in (0,1)$ und genügend große n dann $T(n)=\Theta (f(n))$

Idee

Wir haben folgenden Rekursionsbaum:

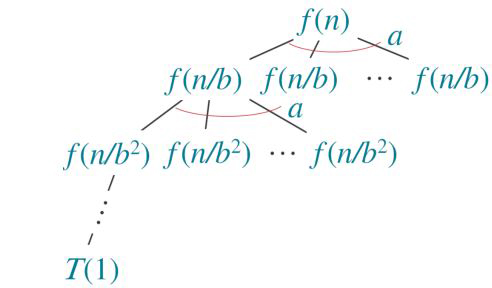
Auf der ersten Ebene ist der Aufwand f(n), auf der zweiten Ebene $af(n/b)$ und auf der dritten Ebene $a^{2}f(n/b^{2})$. Die Höhe des Baumes beträgt $h=log_{b}n$. Die Anzahl der Blätter berechnet sich durch $a^{h}$ und beträgt somit $a^{log_{b}n}=n^{log_{b}a}$.

Fall 1: Das Gewicht wächst geometrisch von der Wurzel zu den Blättern. Die Blätter erhalten einen konstanten Anteil des Gesamtgewichts.

$\Theta (n^{log_{b}a})$

Fall 2: k ist 0 und das Gewicht ist ungefähr das Gleiche auf jedem der $log_{b}a$ Ebenen.

$\Theta (n^{log_{b}a}\cdot ld~n)$

Fall 3: Das Gewicht reduziert sich geometrisch von der Wurzel zu den Blättern. Die Wurzel erhält einen konstanten Anteil am Gesamtgewicht.

$\Theta (f(n))$

Beispiel 1

$T(n)=4T(n/2)+n$

$a=4,b=2\Rightarrow n^{log_{b}a}=n^{log_{2}4}=n^{2}$

$f(n)=n$

Fall 1: $f(n)\in O(n^{2-\epsilon }){\text{für }}\epsilon >0$

$\Rightarrow T(n)=\Theta (n^{2})$

Beispiel 2

$T(n)=4T(n/2)+n^{2}$

$a=4,b=2\Rightarrow n^{log_{b}a}=n^{log_{2}4}=n^{2}$

$f(n)=n^{2}$

Fall 2: $f(n)\in \Theta (n^{2}~ld^{k}~n)\ {\text{für }}k=0$

$\Rightarrow T(n)=\Theta (n^{2}~ld~n)$

Beispiel 3

$T(n)=4T(n/2)+n^{3}$

$a=4,b=2\Rightarrow n^{log_{b}a}=n^{log_{2}4}=n^{2}$

$f(n)=n^{3}$

Fall 3: $f(n)\in \Omega (n^{2+\epsilon }){\text{für }}\epsilon >0$

und $4({\frac {n}{2}})^{3}\leq cn^{3}$ (Regularitätsbedingung)

für $c={\frac {1}{2}}$

$\Rightarrow T(n)=\Theta (n^{3})$

Beispiel 4

$T(n)=4T(n/2)+{\frac {n^{2}}{log~n}}$

$a=4,b=2\Rightarrow n^{log_{b}a}=n^{log_{2}4}=n^{2}$

$f(n)={\frac {n^{2}}{log~n}}$

Welcher Fall liegt nun vor? Das Mastertheorem kann an dieser Stelle nicht benutzt werden, da

• 1. Fall $f(n)\notin O(n^{2-\epsilon })$
• 2. Fall $f(n)\notin \Theta (n^{2}\cdot ld^{k}~n){\text{ für }}k\geq 0$
• 3. Fall $f(n)\notin \Omega (n^{2+\epsilon })$

Nützliche Hinweise

• Basisumrechnung

$log_{b}x={\frac {log_{a}x}{log_{a}b}}\Rightarrow O(log_{b}x)=O(log_{a}x)$

• de L'Hospital

$lim_{x\to \infty }{\frac {f(x)}{g(x)}}=lim_{x\to \infty }{\frac {f'(x)}{g'(x)}}$

• Vergleiche Logarithmus vs. Polynom

$lim_{x\to \infty }log_{b}x=\infty$

$lim_{x\to \infty }x^{\epsilon }=\infty \ {\text{ für }}\epsilon >0$

$lim_{x\to \infty }{\frac {log_{b}x}{x^{\epsilon }}}=lim_{x\to \infty }{\frac {(log_{b}x)'}{(x^{\epsilon })'}}=lim_{x\to \infty }{\frac {\frac {1}{x}}{\epsilon x^{\epsilon -1}}}$ $=lim_{x\to \infty }{\frac {1}{x\epsilon x^{\epsilon -1}}}=lim_{x\to \infty }{\frac {1}{\epsilon x^{\epsilon }}}=0{\text{ für }}\epsilon >0$

Rekursionsbäume

Auf dieser Seite wird das Thema Rekursionsbäume behandelt. Das allgemeine Problem ist, dass man zum Abschätzen von der Aufwandsklasse einer Rekursionsgleichung gute Vermutungen braucht. Doch wie kommt man darauf? Ein Ansatz ist die Veranschaulichung durch einen Rekursionsbaum. Die Aufwandsklasse wird dann durch die Rekursionsbaummethode bestimmt. Das ist sehr nützlich, um eine Lösung zu raten, die danach durch eine andere Methode (z.B. Induktion) gezeigt wird. Rekursionsbäume sind besonders anschaulich bei Divide-and-Conquer-Algorithmen.

Spezialfall Divide and Conquer

Bei MergeSort sehen die Divide and Conquer Schritte wie folgt aus:

1. Divide: Zerteile eine Folge mit n Elementen in zwei Folgen mit je n/2 Elementen.
2. Conquer: Wenn die resultierende Folge 1 oder 0 Elemente enthält,dann ist sie sortiert. Ansonsten wende MergeSort rekursiv an.
3. Combine: Mische die zwei sortierten Teilfolgen.

$T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n\leq 1)\\D(n)+\alpha \cdot T(n/b)+C(n)&{\text{sonst}}\end{array}}\right.$

public List mergeSort(List f) {
  if (f.size() <= 1) {
    return f;
  } else {
    int m = f.size() / 2;
    List left = mergeSort(f.subList(0,m));
    List right = mergeSort(f.subList(m,f.size());
    return merge(left, right);
  }
}

$T(n):=\left\{{\begin{array}{ll}\Theta (1)&{\text{für }}(n\leq 1)\\2\cdot T(n/2)+\Theta (n)&{\text{sonst}}\end{array}}\right.$

Rekursionsbaum

Herleitung des Aufwandes

Die Grundidee ist das wiederholte Einsetzen der Rekursionsgleichung in sich selbst als Baum dargestellt. Das Ziel ist ein Muster zu erkennen. Bei einem Rekursionsbaum beschreibt ein Knoten die Kosten eines Teilproblems. Die Blätter sind die Kosten der Basis fällt T(0) und T(1). Der Aufwand bestimmt sich aus der Summe über alle Ebenen.

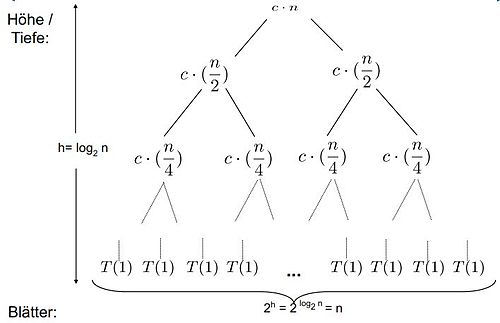
1. Ebene $c\cdot n$

2. Ebene $2\cdot {\frac {1}{2}}\cdot c\cdot n$

3. Ebene $4\cdot {\frac {1}{4}}\cdot c\cdot n$

....

n. Ebene $\Theta (1)\cdot n=\Theta (n)$

Der Aufwand berechnet sich nun wie folgt:

$T(n)=c\cdot n+2\cdot {\frac {1}{2}}\cdot c\cdot n+4\cdot {\frac {1}{4}}\cdot c\cdot n+2^{log_{2}n-1}\cdot {\frac {1}{2^{log_{2}n-1}}}\cdot c\cdot n+\Theta (n)$

$=\sum _{i=0}^{log_{2}n-1}c\cdot n+\Theta (n)$

$=c\cdot n\cdot \sum _{i=0}^{log_{2}n-1}1+\Theta (n)$

$=c\cdot n\cdot log_{2}n+\Theta (n)$

$=\Theta (n\cdot log_{2}n)+\Theta (n)=\Theta (n\cdot log_{2}n)$

Allgemein bestimmt sich der Aufwand T(n) durch die Summe des Aufwands je Ebene und des Aufwands der Blattebene.

Bezogen auf den gegebenen Rekursionsbaum wäre das $T(n)=3\cdot T(n/4)+c\cdot n^{2}$

Literatur

Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 8.3 zu finden.