Kurs:Algorithmen und Datenstrukturen (hsrw)/Druckversion
Pseudocode
[Bearbeiten]Pseudocode ist eine neutrale Sprache, die verständlicher und kürzer ist als reale Programmiersprachen. Die Syntax des hier verwendeten Pseudocodes ist an Pascal angelehnt. Darüberhinaus werden einzelne Sprachelemente von Java (z. B. return) verwendet.
Blöcke
[Bearbeiten]Auf die in Java verwendeten geschwungenen Klammern wird verzichtet. Blöcke sind eingerückt. Auf Semikola zum Abschließen von Anweisungen wird verzichtet.
<Kopf des Blocks>
<Anweisung>
<Anweisung>
<Anweisung hinter dem Block>
Bedingte Ausführung
[Bearbeiten]Auch if Bedingungen mit optionalem else Zweig gibt es analog zu Java. Die Spitzen Klammern haben die Bedeutung, dass es sich bei dem entsprechenden Text nicht um ein Schlüsselwort, sondern um einen Ausdruck (Bedingung oder Anweisung) handelt.
if <Bedingung>
<Anweisung>*
[else
<Anweisung>*]
Schleifen
[Bearbeiten]Es gibt die bekannten kopf- und fußgesteuerten Schleifen sowie Schleifen mit fester Anzahl von Durchläufen.
Kopfgesteuerte Schleifen werden mit while realisiert. Im eingerückten Block stehen eine oder mehrere Anweisungen. Dies wird durch den aus der Vorlesung "Grundlagen der Informatik" bekannten Kleene Stern angezeigt, welcher null bis beliebig viele Wiederholungen des vor ihm stehenden Ausdrucks bedeutet.
while <Bedingung>
<Anweisung>*
Schleifen mit fester Anzahl der Durchläufe werden mit for realisiert. Dort wird eine Zählvariable von einem Initialwert in Einerschritten entweder aufwärts oder abwärts bis zum festgelegten Endwert gezählt. Auch hier gibt es einen eingerückten Block mit Anweisungen.
for <Initialwert> to | downto <Endwert>
<Anweisung>*
Weiterhin gibt es eine fußgesteuerte Schleife. Hier in Form der repeat until Schleife. Wir beginnen mit repeat anschließend folgt ein eingerückter Block mit Anweisungen und schließlich das Schlüsselwort until mit der Endbedingung, mit deren Erfüllung die Schleife verlassen wird.
repeat
<Anweisung>*
until <Endbedingung>
Kommentar
[Bearbeiten]Kommentare leiten wir mit dem doppelten Querstrich ein, sie reichen jeweils bis zum Ende der Zeile.
<Anweisung> // <Kommentar> <Anweisung> <Anweisung> // <Kommentar>
Zuweisungen
[Bearbeiten]Bei Zuweisungen orientieren wir uns an der Syntax von Pascal x := 42. Alternativ findet man in der Literatur häufig die Schreibweise x <- 42.
- Zuweisung x := 42
Vergleichsoperatoren
[Bearbeiten]Weiterhin haben wir Vergleichsoperatoren. Hier verwenden wir ein einzelnes Gleichheitszeichen für die Gleichheit und auch in den weiteren Fällen die üblichen mathematischen Symbole.
- Vergleich = ≠ < > ≤ ≥
Für boolesche Ausdrücke haben wir die Schüsselwörter and, or, not und xor.
Boolesche Operatoren
[Bearbeiten]- Boolsche Ausdrücke and or not xor
Typangaben
[Bearbeiten]Typisierung geben wir nur an, sofern sie nicht aus dem Kontext klar wird. Wir orientieren uns hier auch an der Pascalsyntax x : int.
- Typisierung x : int
In Abweichung zur Literatur verwendeten wir nullbasierte Arrays. Der kleinste Index eines Arrays ist bei uns 0, weil wir dies von Java bereits kennen.
Arrays
[Bearbeiten]- Arrays nullbasiert
Als Buch empfehlen wir Ottmann und Widmeyer: Algorithmen und Datenstrukturen.
Beispielhaft geben wir die Maximumsbestimmung im Pseudocode an. Hierzu legen wir einen Zwischenspeicher an, welchen wir mit jedem Element des Arrays vergleichen und auf das aktuelle Element hochsetzen, falls es größer ist als der aktuelle Wert des Zwischenspeichers. Schlussendlich geben wir den Zwischenspeicher zurück.
max(a : array) : int
m := a[0]
for i := 0 to a.length - 1
if a[i] > m
m := a[i]
return m
Die Länge des Arrays a bezeichnen wir analog zu Java mit a.length.
Suchen
[Bearbeiten]Einleitung Suchen
[Bearbeiten]In diesem Kapitel geben wir einen Überblick über das Thema Suchen. Suchprobleme sind eine der häufigsten Probleme in der Informatik. Man kann in sortierten Folgen suchen, Zeichenketten im Text suchen, Dokumente in Textkorpora suchen, oder allgemeine Lösungen von Problemräumen, wie der Spielbaumsuche oder der Plansuche, suchen. Hier behandeln wir zunächst die Suche in sortierten Folgen.
Motivation
[Bearbeiten]Beim Suchen wiederholt man häufig sehr nützliche Beispielalgorithmen, oder lernt diese sogar neu kennen. Außerdem dient es der Vorbereitung der theoretischen Betrachtungen zur Komplexität von Algorithmen. Des weiteren dient es der informellen Diskussion von Entwurfsentscheidungen.
Suchen in sortierten Folgen
[Bearbeiten]- Annahme:
- Die Folge F ist ein Feld mit numerischen Werten. Dazu ist die Folge sortiert, das heißt, wenn i<j, dann ist F[i]<F[j]. Auf das i-te Element hat man Zugriff über F[i]. Es wird nur der Suchschlüssel berücksichtigt.
Ein Beispiel ist ein Telefonbuch, in dem wir nach Namen suchen möchten. Doch wie repräsentiert man diese Daten?
Einschub lineare Datenstrukturen
[Bearbeiten]Definition
[Bearbeiten]Eine lineare Datenstruktur L ist eine Sequenz . Die lineare Datenstruktur ordnet Elemente (entweder primitive Datentypen oder komplexere Datenstrukturen) in einer linearen Anordnung an.
Beispiel
[Bearbeiten]Zahlenfolgen
| 5 | 4 | 6 | 1 | 3 | 2 |
Strings
| L | I | N | E | A | R |
Atomare Operationen
[Bearbeiten]Zu den Operationen gehören Lesen mit
- get(i): Element an Position i lesen
- first(): erstes Element lesen
- last(): letztes Element lesen
- next(e): Element nach Element e lesen
und Schreiben mit
- set(i,e): Element an Position i auf e setzen
- add(i,e): Element e an Position i einfügen
- del(i): Element an Position i löschen
Arrays und Listen
[Bearbeiten]Es gibt zwei Möglichkeiten lineare Datenstrukturen zu realisieren. Entweder Arrays oder (verlinkte) Listen. Arrays belegen einen zusammenhängenden Bereich im Speicher. Elemente einer verlinkten Liste können beliebig verteilt sein. Ob zur Realisierung einer linearen Datenstruktur ein Array oder eine Liste verwendet wird, hängt von der Anwendung ab. Arrays werden meist für statische Datenstrukturen verwendet, d.h. wenn die Länge des Arrays nicht verändert wird. Listen werden meist für dynamische Datenstrukturen verwendet, d.h. wenn die Länge variabel ist. Zu den positiven Eigenschaften von Arrays zählen der schneller Zugriff auf Einzelelemente durch den Index. Zu den negativen Eigenschaften von Arrays zählen das sehr aufwändige Einfügen der Elemente. Zu den positiven Eigenschaften von Listen zählen die relativ effiziente Manipulation, zu den negativen Eigenschaften der ineffiziente Direktzugriff.
Einfache verlinkte Liste von Zahlen in Java
[Bearbeiten]public class IntegerList {
private class IntegerListElement{
int value;
IntegerListElement next;
}
IntegerListElement first;
int size = 0;
private IntegerListElement getElement(int i){
if(i+1 > size)
throw new IllegalArgumentExcepHon();
int idx = 0;
IntegerListElement current = first;
while(idx != i){
current = current.next;
idx ++;
}
return current;
}
public int get(int i){
return this.getElement(i).value;
}
public int add(int pos, int val){
IntegerListElement newElem = new IntegerListElement();
newElem.value = val;
if(pos > 0){
IntegerListElement e = this.getElement(pos‐1);
newElem.next = e.next;
e.next = newElem;
}else{
newElem.next = this.first;
this.first = newElem;
}
Suchen und Sortieren
[Bearbeiten]Suchen und Sortieren sind voneinander abhängige Operationen. Dabei gibt es zwei Ansätze: Wenn Elemente nie sortiert sind, dann ist die Suche sehr aufwändig. Wenn die Elemente sortiert sind, wird die Suche erleichtert, jedoch kann das Sortieren an sich sehr aufwändig sein. Wenn Elemente hinzugefügt oder gelöscht werden ist diese Problematik noch sichtbarer. Nur ein unsortiertes Element macht die Suche aufwändig, doch bei jeder Einfügung oder Löschung zu sortieren ist ebenfalls sehr aufwändig. Spezielle dynamische Datenstrukturen erlauben eine automatische und effiziente Sortierung bei Einfügung oder Löschung.
Lineare Datenstruktur in Java
[Bearbeiten]- Arrays:
- int[] arr = new int[10];
- arr[1] = 4;
- Listen:
- List<Integer> myList = new LinkedList<Integer>();
- myList.add(5);
- Neben LinkedList unterstützt Java eine Reihe weiterer Listenimplementierungen mit unterschiedlichen Vor- und Nachteilen
- Schnittstelle List<Type> beinhaltet die gemeinsamen Methoden
Suche
[Bearbeiten]- Problembeschreibung
- Die Eingabe ist eine Folge F mit n Elementen von Zahlen und Suchelementen k. Die Ausgabe ist eine erfolgreiche oder nicht erfolgreiche Suche. Erfolgreich ist sie, wenn der Index p ist. Eventuell muss man festlegen, was bei Mehrfachvorkommen passiert. Normalerweise gilt dann das erste Vorkommen. Ist die Suche nicht erfolgreich, dann ist die Ausgabe -1.
- Merkmale der Suche
- Es gibt immer einen Suchschlüssel für Suchelemente, z.B. Zahlen. Außerdem ist eine Suche immer erfolgreich oder erfolglos. Die Suche basiert auf Vergleichsoperationen und die Daten sind zunächst als Feld, bzw. Array, oder Liste dargestellt.
Suchverfahren
[Bearbeiten]In den nachfolgenden Kapiteln lernen Sie die sequentielle, binäre und Fibonacci Suche kennen.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5 zu finden.
Lineare Suche
[Bearbeiten]Dieses Kapitel handelt von der linearen oder sequentiellen Suche. Die Idee dieses Suchalgorithmus ist, dass zuerst das erste Elemente der Liste mit dem gesuchten Elemente verglichen wird, wenn sie übereinstimmen wird der aktuelle Index zurückgegeben. Wenn nicht wird der Schritt mit dem nächsten Element wiederholt. Sollte das gesuchte Element bis zum Ende der Folge nicht gefunden werden, war die Suche erfolglos und -1 wird zurückgegeben.
Algorithmus
[Bearbeiten]
int SeqSearch(int[] F, int k) {
/ * output: Position p (0 ≤ p ≤ n-1) */
}
int n = F.length;
for (int i = 0; i < n; i++) {
if (F[i] == k) {
return i;
}
return -1; }
Dabei ist Int[] die sortierte Folge von int, int k der Suchschlüssel und die Folge F hat die Länge n.
Aufwands Analyse
[Bearbeiten]Das Terminierungs-Theorem besagt, dass der Algorithmus SeqSearch für eine endliche Eingabe nach endlicher Zeit terminiert. Das Korrektheits-Theorem besagt, falls das Array F ein Element k enthält, gibt SeqSearch(F,k) den Indes des ersten Vorkommens von k zurück. Ansonsten gibt SeqSearch(F,k) den Wert -1 zurück Im besten Fall beträgt die Anzahl der Vergleiche 1, das heißt direkt bei dem ersten Suchdurchlauf wird der Suchschlüssel gefunden. Im schlechtesten Fall beträgt die Anzahl der Vergleiche n, das heißt im letzten Suchdurchlauf wird der Suchschlüssel gefunden. Der Durchschnitt bei einer erfolgreichen Suche beträgt (n+1)/2 und der Durchschnitt einer erfolglosen Suche n. Die Folgen müssen nicht sortiert sein. Der Algorithmus SeqSearch hat also eine Worst-Case Laufzeit von .
Sequentielle Suche in Java
[Bearbeiten]
public class SequentialSearch{
public final static int NO_KEY = -1;
static int SeqSearch(int[] F, int k) {
for (int i = 0; i < F.length; i++){
if (F[i] == k)
return i;
} return NO_KEY;
}
public static void main(String[ ] args){
if (args.length != 1) {
System.out.println(''usage: SequentialSearch
<key>'');
return;
}
int[ ] f = {2, 4, 5, 6, 7, 8, 9, 11};
int k = Integer.parseInt(args[0]);
System.out.println(''Sequentiell:“+seqSearch(f,k));
}
}
In der Klasse SeqSearch ist eine Konstante NO_KEY definiert, die als Ergebnis zurückgegeben wird, wenn der gesuchte Wert nicht im Feld gefunden wurde. Die Methode search wird schließlich in der Klassenmethode main aufgerufen, um das Feld f nach dem Schlüsselwert k zu durchsuchen. Dieser Wert ist als Parameter beim Programmaufruf anzugeben. Da die Programmparameter als Feld args von Zeichenketten übergeben werden, ist zuvor noch eine Konvertierung in einen int-Wert mit Hilfe der Methode parseInt der Klasse java.lang.Integer vorzunehmen. Somit bedeutet der Programmaufruf "java SeqSearch 4" die Suche nach dem Wert 4 in der gegebenen Folge. Der Aufruf erfolgt mit java SequentialSearch 4
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.1.1 zu finden.
Binäre Suche
[Bearbeiten]Dieses Kapitel behandelt die binäre Suche. Wir stellen uns die Frage, wie die Suche effizienter werden könnte. Das Prinzip der binären Suche ist zuerst den mittleren Eintrag zu wählen und zu prüfen ob sich der gesuchte Wert in der linken oder rechten Hälfte der Liste befindet. Anschließend fährt man rekursiv mit der Hälfte fort, in der sich der Eintrag befindet. Voraussetzung für das binäre Suchverfahren ist, dass die Folge sortiert ist. Das Suchverfahren entspricht dem Entwurfsmuster von Divide-and-Conquer.
Beispiel
[Bearbeiten]Rekursiver Algorithmus
[Bearbeiten]int BinarySearch(int[] F, int k){
/*input: Folge F der Länge n, Schlüssel k */
/*output: Position p */
return BinarySearchRec(F, k, 0, F.length-1); //initialer Aufruf
}
int BinarySearchRec (int[] F, int k, int u, int o) {
/* input: Folge F der Länge n, Schlüssel k,
untere Schranke u, obere Schranke o */
/* output: Position p */
m = (u+o)/2;
if (F[m] == k) return m;
if ( u == o) return -1;
if (F[m] > k) return BinarySearchRec(F,k,u,m-1);
return BinarySearchRec(F,k,m+1,o);
}
Aufwands Analyse
[Bearbeiten]Das Terminierungs-Theorem besagt, dass der Algorithmus BinarySearch für jede endliche Eingabe F nach endlicher Zeit terminiert. In jedem Rekursionsschritt verkürzt sich die Länge des betrachteten Arrays F um mehr als die Hälfte. Nach endlichen vielen Schritten hat das Array nur noch ein Element und die Suche endet entweder erfolgreich oder erfolglos. Falls das Element vorher gefunden wird terminiert der Algorithmus schon früher.
Das Korrektheits-Theorem besagt, dass falls das Array F ein Element k enthält, gibt BinarySearch(F.k) den Index eines Vorkommens von k zurück. Ansonsten gibt BinarySearch (F,k) den Wert ‐1 zurück. Beweisen kann man das durch die verallgemeinerte Induktion nach der Länge n von F. n=1: Der erste Aufruf von BinarySearchRec ist BinarySearchRec(F,k,0,0) und somit m=0. Ist F[0]=k so wird 0 zurückgegeben, ansonsten ‐1 da 0=0. n>1: Der erste Aufruf von BinarySearchRec ist BinarySearchRec(F,k,0,n‐1) und somit m=(n‐1)/2. Ist F[m]=k, so wird m zurückgegeben. Ansonsten wird rekursiv auf F[0...m‐1] oder F[m+1...n] fortgefahren. Da die Folge sortiert ist, kann k nur in einem der beiden Teile vorhanden sein.
Da die Liste nach jedem Aufruf halbiert wird, haben wir nach dem ersten Teilen der Folge noch n/2 Elemente, nach dem zweiten Schritt n/4 Elemente, nach dem dritten Schritt n/8 Elemente... daher lässt sich allgemein sagen, dass in jedem i-ten Schritt maximal Elemente, das heißt Vergleiche bei der Suche. Im besten Fall hat die Suche nur einen Vergleich, weil der Suchschlüssel genau in der Mitte liegt. Im schlechtesten Fall und im Durchschnitt für eine erfolgreiche und eine erfolglose Suche liegt die Anzahl der Vergleiche bei .
Rekursionsgleichung
[Bearbeiten]Für die erfolglose Suche ergibt sich folgende Rekursionsgleichung.
Das Auflösen von T(n) nach Induktion ergibt eine Laufzeit für eine erfolglose, also Worst-Case, Suche.
Iterativer Algorithmus
[Bearbeiten]int BinarySearch(int[] F, int k) {
/* input: Folge F der Länge n, Schlüssel k */
/* output: Position p (0 ≤ p ≤ n-1) */
int u = 0;
int o = F.length-1;
int m;
while (u <= o) {
m = (u+o)/2;
if (F[m] == k)
return m;
else
if (k < F[m])
o = m-1;
else
u = m+1;
}
return -1;
}
Der erste Teil des Algorithmus ist die Initialisierung. Die while Schleife, besagt, dass so lange wiederholt werden soll, bis die angegebenen Schranken erreicht sind. Die if Anweisung ist die Abbruchbedingung. Der letzte Teil des Algorithmus (else) passt die obere, bzw. untere Schranke an.
Vergleich der Suchverfahren
[Bearbeiten]| Verfahren / #Elemente | ||||
|---|---|---|---|---|
| sequenziell (n/2) | ||||
| binär |
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.1.2 zu finden.
Komplexität
[Bearbeiten]Einführung Komplexität
[Bearbeiten]Auf dieser Seite wird das Thema Komplexität behandelt. Gegeben ist ein zu lösendes Problem. Es ist wünschenswert, dass der Algorithmus zur Berechnung der Lösung einen möglichst geringen Aufwand hat. Daher wird der Aufwand des Algorithmus (Komplexität) abgeschätzt . Zur Lösung von Problemen einer bestimmten Klasse gibt es einen Mindestaufwand.
Motivierendes Beispiel
[Bearbeiten]Als Beispiel nutzen wir die sequentielle Suche in Folgen. Gegeben ist die Zahl b und n Zahlen, z.B. mit A[0...n-1] mit n>0, wobei die Zahlen verschieden sind. Gesucht ist ein Index , falls der Index existiert, sonst ist i = n. Die Lösung für das Problem ist:
i = 0;
while (i < n && b != A[i])
i++;
Der Aufwand der Suche hängt nun von der Eingabe ab, d.h vom gewählten Wert n, den Zahlen A[0],...,A[n] und von b. Es gibt zwei Möglichkeiten, eine erfolgreiche oder eine erfolglose Suche. Eine erfolgreiche Suche haben wir, wenn b=A[i] dann ist S=i+1 Schritte. Ist die Suche jedoch erfolglos, dann ist S=n+1 Schritte. Das Problem ist, dass die Aussage von zu vielen Parametern abhängt und unser Ziel ist eine globale Aussage zu finden, die nur von einer einfachen Größe abhängt, z.B. der Länge n der Folge.
Analyse erfolgreiche Suche
[Bearbeiten]Im schlechtesten Fall wird b erst im letzten Schritt gefunden, d.h. b=A[n-1]. Dann wäre S=n. Im Mittel wird die Anwendung mit verschiedenen Eingaben wiederholt. Wenn man beobachtet wie oft b an erster, zweiter,..., letzter Stelle gefunden wird, hat man eine Annahme über die Häufigkeit. Läuft der Algorithmus k mal (k>1), so wird b gleich oft an erster, zweiter,....,letzter Stelle gefunden und somit k/n mal an jeder Stelle. Die Anzahl der Schritte insgesamt für k Suchvorgänge lässt sich folgendermaßen berechnen:
Für eine Suche benötigt man Schritte Daraus folgt, dass im Mittel ( bei einer Gleichverteilung)
Asymptotische Analyse
[Bearbeiten]Zur Analyse der Komplexität geben wir eine Funktion als Maß für den Aufwand an. . Das bedeutet f(n)=a bei Problemen der Größe n beträgt der Aufwand a. Die Problemgröße ist der Umfang der Eingabe, wie z.B. die Anzahl der zu sortierenden oder zu durchsuchenden Elemente. Der Aufwand ist die Rechenzeit( Abschätzung der Anzahl der Operationen, wie z.B. Vergleiche) und der Speicherplatz.
Aufwand für Schleifen
[Bearbeiten]Wie oft wird die Wertezuweisung x=x+1 in folgenden Anweisungen ausgeführt?
x = x +1
1-mal
for (i = 1; i <= n; i++)
x = x + 1;
n-mal
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
x = x + 1;
-mal
Aufwandsfunktion
[Bearbeiten]Die Aufwandsfunktion ist meist nicht exakt bestimmbar. Daher wird der Aufwand im schlechtesten Fall und im mittleren Fall abgeschätzt und die Größenordnung ungefähr errechnet.
Vergleich Größenordnung
[Bearbeiten]| Funktion | n=100 | n=10.000 | n=100.000 |
| log n | 4,6 | 9,2 | 11,5 |
| 10.000 | 100.000.000 | 10.000.000.000 | |
| 1.000.000 |
Problemstellung
[Bearbeiten]Wie können wir das Wachstum von Funktionen abschätzen und wie verhalten sich die Funktionen zueinander? Das Ziel ist, die Funktion zu wählen, die nach oben beschränkt.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3 zu finden.
O-Notation
[Bearbeiten]Auf dieser Seite wird die O-Notation behandelt. Bei der O-Notation werden die asymptotischen oberen Schranke für Aufwandsfunktion angegeben. Das heißt deren Wachstumsgeschwindigkeit bzw. Größenordnung. Eine Asymptote ist eine Gerade, der sich eine Kurve bei immer größer werdender Entfernung vom Koordinatenursprung unbegrenzt nähert. Eine einfache Vergleichsfunktion ist für Aufwandsfunktionen mit
Definition
[Bearbeiten]Für eine Funktion ist die Menge wie folgt definiert:
Anschaulich formuliert bedeutet das, dass O(f(n)) die Menge aller durch f nach oben beschränkter Funktionen ist und somit die asymptotische obere Schranke ist.
Die Definition veranschaulichst sieht folgendermaßen aus:
Das heißt g wächst nicht schneller als f. Das bedeutet wiederrum ist für genügend große n durch eine Konstante c nach oben beschränkt.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.2 zu finden.
-Notation
[Bearbeiten]Für eine Funktion ist die Menge wie folgt definiert:
Anschaulich formuliert bedeutet das, dass die Menge aller durch f nach unten beschränkter Funktionen ist und somit die asymptotische untere Schranke ist.
-Notation
[Bearbeiten]Die exakte Ordnung von f(n) ist definiert als:
Oder etwas kompakter:
Anschaulich formuliert bedeutet das, dass die Menge aller durch f nach unten und oben beschränkter Funktionen und somit die asymptotische untere und obere Schranke ist.
Beweis
[Bearbeiten]Zu zeigen:
Zeige
Beispiel 1
[Bearbeiten]Wir stellen uns die Frage, ob bzw. ob eine obere Schranke für ist. Die Antwort ist ja. Die Begründung dazu lautet folgendermaßen:
Beispiel 2
[Bearbeiten]Wir stellen uns die Frage, ob bzw. ob eine obere Schranke für ist. Die Antwort ist nein. Beweisen kann man das durch Widerspruch. Unsere Annahme ist:
Wähle Widerspruch!!
Notation Eigenschaften
[Bearbeiten]Lemma
[Bearbeiten]Für beliebige Funktionen f,g gilt:
Beweis in beide Richtungen
[Bearbeiten]
Als erstes machen wir den Beweis nach rechts ()
nun der Beweis nach links ()
Beispiel
[Bearbeiten]
Lemma
[Bearbeiten]1. 2. 3.
Beweis in beide Richtungen
[Bearbeiten]Beweis zu 1. nach rechts ()
Beweis zu 1. nach links ()
(siehe Definition)
und sei t(n) ein beliebiges Element der Menge O(f(n))
(siehe Definition)
(Definition der Teilmenge, da t(n) ein beliebiges Element ist)
Beispiele
[Bearbeiten]
Damit ist
Damit ist
Damit ist
Lemma
[Bearbeiten]Falls , dann ist auch .
Beweis
[Bearbeiten]
Dabei ist eine Konstante.
Beispiel
[Bearbeiten]
Lemma
[Bearbeiten]1. 2.
Ein häufiges Problem sind Grenzwerte der Art oder Bei diesem Problem kann man als Ansatz die Regel von de l'Hospital verwenden.
Satz(Regel von de L'Hospital) Seien f und g auf dem Intervall differenzierbar. Es gelte und es existiere . Dann existiert auch und es gilt:
Beispiel
[Bearbeiten]1.
2.
Beim zweiten Beispiel musste die Regel von de l'Hospital wiederholt angewandt werden.
Lemma
[Bearbeiten]Gibt es immer eine Ordnung zwischen den Funktionen? Es gibt Funktionen f und g mit . Ein Beispiel sind die Funktionen sin(n) und cos(n).
Für alle
Beweis durch Widerspruch
[Bearbeiten]Wir nehmen an, dass ,
das heißt .
Aber es muss auch gelten,
das heißt
Komplexitätsklassen
[Bearbeiten]Auf dieser Seite werden die Komplexitätsklassen behandelt.
Wir sagen sei Und wir sagen, ein Algorithmus mit Komplexität f(n) benötigt höchstens polynomielle Rechenzeit, falls es ein Polynom p(n) gibt, mit . Des weiteren sagen wir, dass ein Algorithmus höchstens exponentielle Rechenzeit benötigt, falls es eine Konstante gibt, mit .
Die Komplexitätsklassen sind:
| der konstante Aufwand, das bedeutet der Aufwand ist nicht abhängig von der Eingabe | |
| der logarithmische Aufwand | |
| der lineare Aufwand | |
| der quadratische Aufwand | |
| der polynomiale Aufwand | |
| der exponentielle Aufwand |
Wachstum
[Bearbeiten]| f(n) | n=2 | ||||
| ldn | 1 | 4 | 8 | 10 | 20 |
| n | 2 | 16 | 256 | 1024 | 1048576 |
| 2 | 64 | 2048 | 10240 | 20971520 | |
| 4 | 256 | 65536 | 1048576 | ||
| 8 | 4096 | 16777200 | |||
| 4 | 65536 |
Zeitaufwand
[Bearbeiten]Nun stellen wir uns die Frage, wie groß bezüglich der Rechenschritte darf, oder kann ein Problem sein, je nach Komplexitätsklasse, wenn die Zeit T begrenzt ist? Wir nehmen an, dass wir pro Schritt eine Rechenzeit von brauchen. In der folgenden Tabelle steht T für die Zeitbegrenzung und G für die maximale Problemgröße.
| G | T=1Min. | 1 Std. | 1 Tag | 1 Woche | 1 Jahr |
| n | |||||
| 7750 | |||||
| 391 | 1530 | 4420 | 8450 | 31600 | |
| 25 | 31 | 36 | 39 | 44 |
Ein Beispiel ist für T=1 Min. :
Typische Problemklassen
[Bearbeiten]| Aufwand | Problemklasse |
|---|---|
| für einige Suchverfahren für Tabellen (Hashing) | |
| für allgemeine Suchverfahren für Tabellen (Baum-Suchverfahren) | |
| für sequenzielle Suche, Suche in Texten, syntaktische Analyse von Programmen (bei "guter" Grammatik) | |
| für Sortieren | |
| für einige dynamische Optimierungsverfahren (z.B. optimale Suchbäume), einfache Multiplikation von Matrix-Vektor | |
| für einfache Matrizen Multiplikationen | |
| für viele Optimierungsprobleme (z.B. optimale Schaltwerke), automatisches Beweisen (im Prädikatenkalkül 1.Stufe) |
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.3 zu finden.
Aufwandsanalyse von iterativen Algorithmen
[Bearbeiten]Auf dieser Seite wird der Aufwand von iterativen Algorithmen analysiert. Als Aufwand wird die Anzahl der durchlaufenen Operationen zur Lösung des Problems bezeichnet ( Zuweisungen, Vergleiche...). Häufig ist der Aufwand abhängig vom Eingabeparameter (Problemgröße). Die Aufwandsklasse sagt, wie der Aufwand in Abhängigkeit von der Problemgröße wächst. Doch wie kann man nun bei beliebigem Java Code die Aufwandsklasse bestimmen?
Aufwand von Programmen ablesen
[Bearbeiten]void alg1(int n){
int m = 2;
int i;
int k = n;
while (n > 0){
i = k;
while (i > 0) {
m = m + i;
i = i / 2;
}
n = n - 1;
}
}
Die Aufwandsklasse ist . Die äußere Schleife wird n-mal durchlaufen und die Innere Schleife log n-mal.
void alg1(int n) {
int m = 1;
int i = 0;
while (m < n) {
while (i < m)
i = i + 1;
m = m + i;
}
}
Hier ist die Aufwandsklasse O(n+log n). In jedem Durchlauf der äußeren Schleife wird m verdoppelt, d.h. sie läuft log n Mal. Die innere Schleife läuft bis n/2, aber nicht jedes Mal, weil i nur ein Mal auf 0 gesetzt wird. Man könnte als Aufwandsklasse auch O(n) sagen, da der Summand log n nicht ins Gewicht fällt.
Bestandteile iterativer Algorithmen
[Bearbeiten]Zum einen haben wir elementare Anweisungen wie Zuweisungen und Vergleiche. Diese haben einen Aufwand von 1.
Des Weiteren haben wir Sequenzen oder auch geschrieben. Die obere Grenze ist und die untere Grenze ist . Dabei ist der Aufwand, der bei der Ausführung von entsteht.
Ein weiterer Bestandteil ist die Selektion. . Hier ist die obere Grenze und die untere Grenze .
Außerdem haben wir Iterationen . Hierbei ist die obere und die untere Grenze die Anzahl der Schleifendurchläufe, und die untere Grenze . Doch wie ist der Aufwand für eine for-Schleife? Ein Beispiel ist . Die Antwort ist die Abbildung auf eine while-Schleife.
while(B) {
}
Beispiel Sequenz
[Bearbeiten]public int berechne(int n) {
int x = 0;
x = x + 1;
return x;
}
Jede Zeile hat den Aufwand . Wie viele Operationen werden nun durchlaufen? Und ist die Anzahl abhängig vom Eingabeparameter? Der Aufwand ist
Die Aufwandsklasse ist somit
Beispiel Schleifen
[Bearbeiten]public int berechne(int n) {
int x = 0;
for (int i=0; i < n; i++) {
x = x + 1;
}
return x;
}
Die for Schleife hat den Aufwand . Die Initialisierung und das return haben jeweils den Aufwand .
Der Gesamtaufwand ist somit . Somit ist die Aufwandsklasse .
public int berechne(int n) {
int x = 0;
for (int i=0; i < n; i++) {
for (int j=0; j < n; j++) {
x = x + 1;
}
}
return x;
}
Hier hat die for-Schleife den Aufwand und die Initialisierung und das return wieder . Damit ergibt der sich Gesamtaufwand . Daraus folgt die Aufwandsklasse .
Beispiel Selektion
[Bearbeiten]public int berechne(int n) {
if (n % 2 == 0) {
int x = 0;
for (int i=0; i < n; i++) {
x = x + 1;
}
return x;
}else{
return n;
}
}
Hier hat die for-Schleife einen Aufwand von . Die Initialisierung und das return wieder .
Die obere Grenze ist somit und die untere Grenze
Faustregeln
[Bearbeiten]Zu den häufig verwendeten Faustregeln gehört, dass wenn wir keine Schleife haben, der Aufwand konstant ist. Eine weitere ist, dass bei einer Schleife immer ein linearer Aufwand vorliegt. Bei zwei geschachtelten Schleifen haben wir immer einen quadratischen Aufwand. Doch die Faustegeln gelten nicht ohne Ausnahmen. Besonders Acht geben muss man bei Aufwandsbestimmungen für Schleifen, bei mehreren Eingabevariablen, bei Funktionsaufrufen und bei Rekursionen.
Aufwandsbestimmung für Schleifen
[Bearbeiten]public int berechne(int n) {
int x = 0;
for (int i=0; i < 5; i++) {
x = x + 1;
}
return x;
}
Der Schleifenabbruch hängt nicht vom Eingabeparameter ab. Der Aufwand beträgt somit haben wir die Aufwandsklasse
public int berechne(int n) {
int x = 0;
for (int i=1; i < n; i = 2*i) {
x = x + 1;
}
return x;
}
Hier wächst die Laufvariable nicht linear an.Daher ist der Aufwand und wir haben die Aufwandsklasse .
Doch gibt es eine allgemeine Methodik zum Bestimmen des Schleifenaufwands?
for (int i=1; i < n; i=2*i) {
x = x + 1;
}
Schritt 1: Wie entwickelt sich hier die Laufvariable? Der Startwert i ist 1 und die Veränderung in jedem Schritt ist . Die Laufvariable entwickelt sich somit wie folgt:
Nach dem 1. Durchlauf
Nach dem 2. Durchlauf
Nach dem 3. Durchlauf
Nach dem k. Durchlauf
Schritt 2: Nach wie vielen Durchläufen wird die Schleife abgebrochen?
Der Abbruch erfolgt, wenn
:
Somit erfolgt ein Abbruch nach ⌈ ⌉ Durchläufen.
public int berechne(int[] f1, int[] f2) {
int result = 0;
for (int i=0; i < f1.length; i++) {
for (int j=0; j < f2.length; j++) {
if (f1[i] == f2[j]) result++;
}
}
return result;
}
Hier haben wir nun eine for Schleife mit mehreren Eingabevariablen. Die Problemgrößen sind .
public int berechne2(int[] f1, int[] f2){
f2 = mergeSort(f2);
int result = 0;
for (int i=0; i < f1.length; i++) {
if (binarySearch(f2, f1[i])) result++;
}
return result;
}
Der Aufwand ist hier . Somit ist die Aufwandsklasse .
In diesem Beispiel haben wir wieder mehreren Eingabevariablen. Diese sind die gleichen Problemgrößen .
public int berechne2(int[] f1, int[] f2){
int result = 0;
for (int i=0; i < f1.length; i++) {
for (int j=0; j < f2.length; j++) {
if (f1[i] == f2[j]) result++;
}
}
return result;
}
Der Aufwand ist hier wie folgt: . Somit ist die Aufwandsklasse .
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.4 zu finden.
Aufwandsanalyse von rekursiven Algorithmen
[Bearbeiten]Auf dieser Seite wird der Aufwand von rekursiven Algorithmen untersucht.
public int fib(int n) {
if (n == 0 || n == 1) {
return 1;
} else {
return fib(n-1) + fib(n-2);
}
}
Wie ist nun der Aufwand für Fibonacci? Bei Rekursionsabbruch und im Rekursionsfall . Zur Bestimmung benutzen wir Rekursionsgleichungen.
Rekursionsgleichungen
[Bearbeiten]Eine Rekursionsgleichung ist eine Gleichung oder Ungleichung, die eine Funktion anhand ihrer Anwendung auf kleinere Werte beschreibt.
Rekursionsgleichung für Fibonacci:
Lösung von Rekursionsgleichungen
[Bearbeiten]Die Frage ist nun welche Aufwandklasse T(n) beschreibt. Dies könnten alle möglichen Aufwandsklassen sein. Methoden um dieses Problem zu lösen sind die vollständige Induktion und das Master-Theorem.
Spezialfall Divide and Conquer Algorithmus
[Bearbeiten]Ein Divide-and-Conquer Algorithmus stellt im Allgemeinen eine einfache, rekursive Version eines Algorithmus dar und hat drei Schritte:
- Divide: Unterteile das Problem in eine Zahl von Teilproblemen
- Conquer: Löse das Teilproblem rekursiv. Wenn das
Teilproblem klein genug ist, dann löse das Teilproblem direkt (z.B. bei leeren oder einelementigen Listen)
- Combine: Die Lösungen der Teilprobleme werden zu einer Gesamtlösung kombiniert.
Merge Sort ist beispielsweise ein Divide and Conquer Algorithmus.
- Divide: Zerteile eine Folge mit n Elementen in zwei Folgen mit je n/2 Elementen.
- Conquer: Wenn die resultierende Folge 1 oder 0 Elemente enthält, dann ist sie sortiert.Ansonsten wende Merge Sort rekursiv an.
- Combine: Mische die zwei sortierten Teilfolgen.
public List mergeSort(List f) {
if (f.size() <= 1) {
return f;
} else {
int m = f.size() / 2;
List left = mergeSort(f.subList(0,m));
List right = mergeSort(f.subList(m,f.size());
return merge(left, right);
}
}
Die dazugehörige Rekursionsgleichung lautet:
Im Allgemeinen ist die Rekursionsgleichung für Divide and Conquer Algorithmen:
mit D(n) als Aufwand für Divide, T(n/b) als Aufwand für Conquer und C(n) als Aufwand für Combine.
Ab- und Aufrunden
[Bearbeiten]Die Rekursionsgleichung von MergeSort beschreibt den Aufwand für den schlechtesten Fall.
Aber die Annahme, dass n eine geeignete ganze Zahl ist ergibt normalerweise das gleiche Ergebnis wie
eine beliebige Zahl mit Auf- bzw. Abrunden. Dies führt zur einfacheren Rekursionsgleichung:
Beispiel Binäre Suche
[Bearbeiten]public List binarySearch(ArrayList<Integer> f, int e) {
if (f.size() == 0) {
return -1;
} else {
int m = f.size() / 2;
if (f.get(m) == e) {
return m;
} else if (f.get(m) < e) {
return binarySearch(f.subList(0, m), e);
} else {
return binarySearch(f.subList(m+1, f.size()), e);
}
}
}
Die Rekursionsgleichung lautet
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.3.4 zu finden.
Vollständige Induktion
[Bearbeiten]Auf dieser Seite wird die vollständige Induktion behandelt. Es handelt sich hierbei um eine rekursive Beweistechnik aus der Mathematik. Sie ist gut geeignet, um Eigenschaften von rekursiv definierten Funktionen zu beweisen.
Vorgehen
[Bearbeiten]Zunächst vermutet man eine Eigenschaft (z.B. Aufwandsklasse einer Rekursionsgleichung). Nun folgt der Induktionsanfang: Eigenschaft hält für ein kleines n. Als nächstes folgt der Induktionsschritt: Die Annahme ist, dass wir es bereits für ein kleineres n gezeigt haben und wenn die Eigenschaft für kleinere n hält, dann hält sie auch für das nächstgrößere n!
Beispiel 1
[Bearbeiten]
Nun wollen wir die obere Grenze für den Aufwand bestimmen. Unsere Vermutung ist, dass . Nun müssen wir zeigen, dass ( siehe Definition der O-Notation). Die vereinfachte Annahme lautet . Hierbei werden keine Spezialfälle behandelt und im Induktionsschritt wird von nach n gegangen.
Induktionsvermutung:
Induktionsschritt: Wir beweisen von
zu zeigende obere Grenze:
Rekursionsgleichung einsetzen:
Induktionsvermutung einsetzen:
Somit ist der Induktionsschritt erfolgreich, wenn .
Induktionsanfang
Wir zeigen die Induktionsvermutung für einen Anfangswert, am einfachsten ist es, dies für den Rekursionsabbruch zu zeigen.
Zu zeigende obere Grenze:
Rekursionsgleichung einsetzen:
Der Induktionsanfang ist erfolgreich, wenn ist. Doch wann können wir zeigen, dass ist? Für den Wert, den wir im Induktionsanfang gezeigt haben, also für und wenn .
Beispiel 2
[Bearbeiten]
Nun wollen wir die obere Grenze für den Aufwand bestimmen. Unsere Vermutung ist, dass . Nun müssen wir zeigen, dass . Die vereinfachte Annahme lautet .
Induktionsvermutung:
Induktionsschritt: Wir beweisen von
Das Problem ist nun, dass wir den Induktionsschritt für positive n zeigen wollen und nicht für negative, daher müssen wir neu ansetzen.
Induktionsvermutung:
Dabei gibt es folgenden Trick: Modifiziere die Induktionsvermutung, in dem ein kleineres Polynom addiert wird.
Induktionsschritt: Wir beweisen von
Induktionsanfang für n=1
Wann können wir nun zeigen, dass ?
Für . Somit haben wir gezeigt, dass
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 7.2.5 zu finden.
Mastertheorem
[Bearbeiten]Auf dieser Seite wird das Master Theorem behandelt. Die Mastermethode ist ein „Kochrezept“ zur Lösung von Rekursionsgleichungen der Form:
mit den Konstanten , f(n) ist eine asymptotische, positive Funktion, d.h.
- a steht dabei für die Anzahl der Unterprobleme.
- n/b ist die Größe eines Unterproblems
- T(n/b) ist der Aufwand zum Lösen eines Unterproblems (der Größe n/b)
- f(n) ist der Aufwand für das Zerlegen und Kombinieren in bzw. von Unterproblemen
Bei der Mastermethode handelt es sich um ein schnelles Lösungsverfahren zur Bestimmung der Laufzeitklasse einer gegebenen rekursiv definierten Funktion. Dabei gibt es 3 gängige Fälle:
- Fall 1: Obere Abschätzung
- Fall 2: Exakte Abschätzung
- Fall 3: Untere Abschätzung
Lässt sich keiner dieser 3 Fälle anwenden, so muss die Komplexität anderweitig bestimmt werden und wir müssen Voraussetzungen für die Anwendung des Mastertheorems überprüfen.
Dafür vergleicht man mit . Wir verstehen n/b als . Im Folgenden verwenden wir die verkürzte Notation .
Fall 1
[Bearbeiten]Wenn . Daraus folgt, dass f(n) polynomiell langsamer wächst als um einen Faktor . Damit haben wir die Lösung .
Fall 2
[Bearbeiten]Wenn . Daraus folgt, dass f(n) und vergleichbar schnell wachsen. Damit haben wir die Lösung .
Fall 3
[Bearbeiten]Wenn und die Regularitätsbedingung für eine Konstante und genügend große n erfüllt. Daraus folgt, dass f(n) polynomiell schneller wächst als um einen Faktor und f(n) erfüllt die sogenannte Regularitätsbedingung. Damit haben wir die Lösung .
Bedeutung
[Bearbeiten]In jedem Fall vergleichen wir f(n) mit . Intuitiv kann man sagen, dass die Lösung durch die größere Funktion bestimmt wird. Im zweiten Fall wachsen sie ungefähr gleich schnell. Im ersten und dritten Fall muss f(n) nicht nur kleiner oder größer als sein, sondern auch polynomiell kleiner oder größer um einen Faktor . Der dritte Fall kann nur angewandt werden, wenn die Regularitätsbedingung erfüllt ist.
Regularitätsbedingung
[Bearbeiten]Doch wozu wird die Regularitätsbedingung benötigt? Zur Erinnerung, im dritten Fall dominiert f(n) das Wachstum von T(n). Wir müssen an dieser Stelle sicherstellen, dass auch bei rekursivem Anwenden, also wenn die Argumente kleiner werden, T(n) von f(n) dominiert wird. Veranschaulicht heißt das:
für Das Wachstum muss durch f(n) dominiert werden und darf f(n) nicht dominieren.
Die Regularitätsbedingung gilt wenn sie für f(n) und g(n) gilt auch für und auch für
Nachweis für
Voraussetzung ist, dass die Regularitätsbedingung für f(n) und g(n) gilt, d.h.:
Für gilt:
man wählt
und
Nachweis für
Voraussetzung ist, dass die Regularitätsbedingung für f(n) und g(n) gilt, d.h.:
Für gilt:
man wählt
und
Überblick
[Bearbeiten]Ist T(n) eine rekursiv definierte Funktion der Form
Dann gilt:
- 1. Fall: Wenn
- 2. Fall: Wenn
- 3. Fall: Wenn und und genügend große n dann
Idee
[Bearbeiten]Wir haben folgenden Rekursionsbaum:
Auf der ersten Ebene ist der Aufwand f(n), auf der zweiten Ebene und auf der dritten Ebene . Die Höhe des Baumes beträgt . Die Anzahl der Blätter berechnet sich durch und beträgt somit .
Fall 1: Das Gewicht wächst geometrisch von der Wurzel zu den Blättern. Die Blätter erhalten einen konstanten Anteil des Gesamtgewichts.
Fall 2: k ist 0 und das Gewicht ist ungefähr das Gleiche auf jedem der Ebenen.
Fall 3: Das Gewicht reduziert sich geometrisch von der Wurzel zu den Blättern. Die Wurzel erhält einen konstanten Anteil am Gesamtgewicht.
Beispiel 1
[Bearbeiten]
Fall 1:
Beispiel 2
[Bearbeiten]
Fall 2:
Beispiel 3
[Bearbeiten]
Fall 3:
und (Regularitätsbedingung)
für
Beispiel 4
[Bearbeiten]
Welcher Fall liegt nun vor? Das Mastertheorem kann an dieser Stelle nicht benutzt werden, da
- 1. Fall
- 2. Fall
- 3. Fall
Nützliche Hinweise
[Bearbeiten]- Basisumrechnung
- de L'Hospital
- Vergleiche Logarithmus vs. Polynom
Rekursionsbäume
[Bearbeiten]Auf dieser Seite wird das Thema Rekursionsbäume behandelt. Das allgemeine Problem ist, dass man zum Abschätzen von der Aufwandsklasse einer Rekursionsgleichung gute Vermutungen braucht. Doch wie kommt man darauf? Ein Ansatz ist die Veranschaulichung durch einen Rekursionsbaum. Die Aufwandsklasse wird dann durch die Rekursionsbaummethode bestimmt. Das ist sehr nützlich, um eine Lösung zu raten, die danach durch eine andere Methode (z.B. Induktion) gezeigt wird. Rekursionsbäume sind besonders anschaulich bei Divide-and-Conquer-Algorithmen.
Spezialfall Divide and Conquer
[Bearbeiten]Bei MergeSort sehen die Divide and Conquer Schritte wie folgt aus:
- Divide: Zerteile eine Folge mit n Elementen in zwei Folgen mit je n/2 Elementen.
- Conquer: Wenn die resultierende Folge 1 oder 0 Elemente enthält,dann ist sie sortiert. Ansonsten wende MergeSort rekursiv an.
- Combine: Mische die zwei sortierten Teilfolgen.
public List mergeSort(List f) {
if (f.size() <= 1) {
return f;
} else {
int m = f.size() / 2;
List left = mergeSort(f.subList(0,m));
List right = mergeSort(f.subList(m,f.size());
return merge(left, right);
}
}
Rekursionsbaum
[Bearbeiten]Herleitung des Aufwandes
[Bearbeiten]Die Grundidee ist das wiederholte Einsetzen der Rekursionsgleichung in sich selbst als Baum dargestellt. Das Ziel ist ein Muster zu erkennen. Bei einem Rekursionsbaum beschreibt ein Knoten die Kosten eines Teilproblems. Die Blätter sind die Kosten der Basis fällt T(0) und T(1). Der Aufwand bestimmt sich aus der Summe über alle Ebenen.
1. Ebene
2. Ebene
3. Ebene
....
n. Ebene
Der Aufwand berechnet sich nun wie folgt:
Allgemein bestimmt sich der Aufwand T(n) durch die Summe des Aufwands je Ebene und des Aufwands der Blattebene.
Bezogen auf den gegebenen Rekursionsbaum wäre das
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 8.3 zu finden.
Sortieren
[Bearbeiten]Sortieren Grundlagen
[Bearbeiten]Dieses Kapitel gibt eine grundlegende Einführung in das Thema Sortieren. Sortieren ist ein grundlegendes Problem in der Informatik. Es beinhaltet das Ordnen von Dateien mit Datensätzen, die Schlüssel enthalten und das Umordnen der Datensätze, so, dass eine klar definierte Ordnung der Schlüssel (numerisch/alphabetisch) besteht. Eine Vereinfachung ist die Betrachtung der Schlüssel, z.B. ein Feld von int-Werten.
Ordnung
[Bearbeiten]- Partielle Ordnung
- Sei M eine Menge und binäre Relation.
- Es gilt:
- Reflexivität
- Transitivität
- Antisymmetrie
- Es gilt:
- Strikter Anteil einer Ordnungsrelation
- Totale Ordnung
- Partielle Ordnung
- Trichotomie ("Dreiteilung")
Grundbegriffe
[Bearbeiten]Das Verfahren ist intern, wenn auf Hauptspeicherstruktur, wie Felder und Listen sortiert wird. Hingegen ist es extern, wenn die Datensätze auf externen Medien, wie Festplatten und weitere sortiert werden. Die Annahmen sind eine totale Ordnung, aufsteigend vs. absteigend und der Platzbedarf.
Problembeschreibung
[Bearbeiten]Als Eingabe haben wir eine Folge von Zahlen . Als Ausgabe haben wir die Permutation der Zahlen mit der Eigenschaft . Die Sortierung erfolgt nach einem Schlüssel, z.B. Zahlen. In Programmen ist es übertragbar auf beliebige Datenstrukturen mit Schlüssel.
Stabilität
[Bearbeiten]Ein Sortierverfahren heißt stabil, wenn es die relative Reihenfolge gleicher Schlüssel in der Datei beibehält. Beispiel: alphabetisch geordnete Liste von Personen soll nach Alter sortiert werden. Personen mit gleichem Alter sollen weiterhin alphabetisch geordnet bleiben:
Name Alter Name Alter Aristoteles 24 Aristoteles 24 Platon 28 SORTIEREN → Platon 28 Sokrates 30 Theophrastos 28 Theophrastos 28 Sokrates 30
Sortieralgorithmen
[Bearbeiten]Java Stub
[Bearbeiten]public class InsertionSort extends Sort {
/*
* Sortiert die Sequenz a nach dem Verfahren
* „Sortieren durch Einfügen“
*/
@Override
public void execute(int[] a) {
// Elemente: a[0], … , a[n-1]
int n=a.length;
int x;
int j;
// HIER KOMMT DER SORTIERALGORITHMUS
// assert: a[0] <= … <= a[n-1]
}
}
Vergleichsbasiertes Sortieren
[Bearbeiten]Das vergleichbasierte Sortieren ist ein wichtiger Spezialfall des Sortierproblems. Zur Sortierung können nur direkte Vergleiche zweier Werte benutzt werden. Der Wertebereich der Schlüssel kann beliebig sein. Als Eingabe haben wir ein Array ganzer Zahlen und als Ausgabe ein sortiertes Array mit den selben Zahlen mit erhaltenen Mehrfachvorkommen. Einige Sortierverfahren sind effizienter, wenn Listen anstatt Arrays benutzt werden.
Sortierinterface in Java
[Bearbeiten]public interface Sort {
/**
* sorts the given array.
* @param toSort - array to sort.
*/
public void execute(int[] toSort);
}
Ausblick
[Bearbeiten]Auf den folgenden Seiten werden die Sortieralgorithmen Insertion Sort, Selection Sort, Merge Sort und Quick Sort behandelt.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2 zu finden.
InsertionSort
[Bearbeiten]Dieses Kapitel behandelt die Sortiermethode InsertionSort oder auch Sortieren durch Einfügen genannt. Die Idee des Algorithmus ist, die typische menschliche Vorgehensweise, etwa beim Sortieren eines Stapels von Karten umzusetzen. Das heißt es wird mit der ersten Karte ein neuer Stapel gestartet. Anschließend nimmt man jeweils die nächste Karte des Originalstapels und fügt diese an der richtigen Stelle im neuen Stapel ein.
Beispiel
[Bearbeiten]Java Code
[Bearbeiten]void InsertionSort(int[] F) {
int m,j;
for (int i = 1; i < F.length; i++){
j = i;
m = F[i];
while (j > 0 && F[j-1] > m) {
/*verschiebe F[j-1] nach rechts */
F[j] = F[j-1];
j--;
}
F[j] = m;
}
}
Das Array hat F.length viele Elemente von Position 0 bis F.Length-1. Wenn F[j-1] größer m ist, dann wird F[j-1] nach rechts verschoben. Am Ende des Algorithmus wird F[i] an Position F[j] gesetzt.
Analyse
[Bearbeiten]Theorem der Terminierung
[Bearbeiten]Das Theorem der Terminierung besagt, dass der Algorithmus InsertionSort für jede Eingabe int[] F nach endlicher Zeit terminiert.
Beweis
[Bearbeiten]Die Laufvariable i in der äußeren for‐Schleife wird in jedem Durchgang um eins erhöht und wird damit irgendwann die Abbruchbedingung (eine Konstante)erreichen. Die Laufvariable j der inneren while‐Schleife wird in jedem Durchgang um eins verringert und somit die Schleifenbedingung j>0 irgendwann nicht mehr erfüllen.
Theorem der Korrektheit
[Bearbeiten]Das Theorem der Korrektheit besagt, dass der Algorithmus InsertionSort das Problem des vergleichsbasierten Sortierens löst. Beweisen
Beweis
[Bearbeiten]Wir zeigen, dass die folgende Aussage eine Invariante der äußeren for‐Schleife ist (d.h. sie ist am Ende eines jeden Schleifendurchgangs gültig): Das Teilarray F[0..i] ist sortiert Damit gilt auch, dass nach Abbruch der for‐Schleife das Array F[0..n]=F (mit n=F.length‐1) sortiert ist. Zu zeigen ist nun, dass am Ende jeden Durchgangs der äußeren for Schleife F[0...i] sortiert ist. Dies wird durch Induktion nach i gezeigt. Für i=1 gilt im ersten Durchgang wird das erste Element F[0] mit dem zweiten Element F[1] verglichen und ggfs. getauscht um Sortierung zu erreichen (while‐Bedingung). Für gilt angenommen F[0...i] ist am Anfang der äußeren for‐Schleife im Durchgang i+1 sortiert. In der while‐Schleife werden Elemente solange einen Platz weiter nach hinten verschoben, bis ein Index k erreicht wird, sodass alle Elemente mit Index 0..k‐1 kleiner/gleich dem ursprünglichen Element an Index i+1 sind (Induktionsbedingung) und alle Elemente mit Index k+1...i+1 größer sind (while‐Bedingung). Das ursprüngliche Element an Index i+1 wird dann an Position k geschrieben. Damit gilt, dass F[0...i+1] sortiert ist.
Theorem der Laufzeit
[Bearbeiten]Das Theorem der Laufzeit besagt, dass die Anzahl der Vergleichsoperationen von Insertion Sort im besten Fall ist und im durchschnittlichen und schlechtesten .
Beweis
[Bearbeiten]Für die Aufwandsanalyse sind die Anzahl der Vertauschungen und der Vergleiche relevant. Allerdings dominieren die Vergleiche die Vertauschungen, das heißt es werden wesentlich mehr Vergleiche als Vertauschungen benötigt. Wir müssen in jedem Fall alle Elemente i:=1 bis n-1 durchgehen, d.h. immer Faktor n-1 für die Anzahl der Vergleiche. Dann müssen wir zur korrekten Einfügeposition zurückgehen
Im besten Fall ist die Liste schon sortiert. Die Einfügeposition ist gleich nach einem Schritt an Position i-1, d.h. die Anzahl der Vergleiche ist gleich der Anzahl der Schleifendurchläufe = n-1. Bei jedem Rückweg zur Einfügeposition nimmt man den Faktor 1. Somit beträgt die Gesamtzahl der Vergleiche: . Für große Listen lässt sich abschätzen. Damit haben wir einen linearen Aufwand.
Im mittleren Fall ist die Liste unsortiert. Die Einfügeposition befindet sich wahrscheinlich auf der Hälfte des Rückwegs. Bei jedem der n-1 Rückwege, muss ein (i-1)/2 Vergleich addiert werden. Die Gesamtzahl der Vergleiche beträgt dann:
Daraus ergibt sich ein quadratischer Aufwand, wenn konstante Faktoren nicht berücksichtigt werden.
Im schlechtesten Fall ist die Liste absteigend sortiert. Die Einfügeposition befindet sich am Ende des Rückgabewertes bei Position 1. Bei jedem der n-1 Rückwege müssen i-1 Elemente verglichen werden (d.h. alle vorherigen Elemente F[1...i-1]). Analog zu vorhergehenden Überlegungen, gibt es hier aber die doppelte Rückweglänge. Daraus ergibt sich die Gesamtanzahl der Vergleiche:
Daraus ergibt sich ein quadratischer Aufwand, wenn konstante Faktoren nicht berücksichtigt werden.
Optimierung
[Bearbeiten]In der vorgestellten Version des Algorithmus wird die Einfügeposition eines Elements durch (umgekehrte) sequenzielle Suche gefunden. Verwendet man hier binäre Suche (das Teilarray vor dem aktuellen Element ist sortiert!) kann die Anzahl der Vergleichsoperationen gesenkt werden zu O(n log n) (genauere Analyse zeigt, dass die Zahl noch kleiner ist)
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.2 zu finden.
SelectionSort
[Bearbeiten]Dieses Kapitel behandelt die Suchmethode SelectionSort. Die Idee dieses Suchalgorithmus ist, den jeweils größten Wert im Array zu suchen und diesen an die letzte Stelle zu tauschen. Anschließend fährt man mit der um 1 kleineren Liste fort.
Beispiel
[Bearbeiten]Java Code
[Bearbeiten]void SelectionSort(int[] F) {
int marker = F.length -1;
while (marker >= 0) {
/*bestimme größtes Element links v. Marker*/
int max = 0; /* Indexposition*/
for (int i = 1; i <= marker; i++){
if (F[i] > F[max])
max = i;
swap(F, marker, max);
marker--; /*verkleinere Array */
}
void swap(int[] F, int idx1, int idx2) {
int tmp = F[idx1];
F[idx1] = F[idx2];
F[idx2] = tmp;
}
In Java benutzt man die Hilfsmethode swap, welche zwei Elemente im Array vertauscht.
Analyse
[Bearbeiten]Theorem der Terminierung
[Bearbeiten]Das Theorem der Terminierung besagt, dass der Algorithmus SelectionSort für jede Eingabe int[]F nach endlicher Zeit terminiert.
Beweis
[Bearbeiten]Die Variable marker wird zu Anfang des Algorithmus auf einen positiven endlichen Wert gesetzt und in jedem Durchgang der äußeren while‐Schleife um 1 verkleinert. Abbruch der while Schleife erfolgt, wenn marker kleiner 0 ist, also wird die while‐Schleife endlich of durchlaufen. Die innere for‐Schleife hat in jedem Durchgang marker‐viele (also endlich viele) Durchläufe.
Theorem der Korrektheit
[Bearbeiten]Das Theorem der Korrektheit besagt, dass der Algorithmus SelectionSort das Problem des vergleichsbasierten Sortierens löst.
Beweis
[Bearbeiten]Es gilt zunächst, dass die innere for‐Schleife stets den Index des Maximums des Teilarrays F[0...marker] berechnet und in max speichert. Weiterhin gilt, dass die Methode swap(F, marker, max) die Werte F[marker] und F[max] vertauscht.
Wir zeigen nun, dass die folgenden Aussagen Invariante der äußeren while-Schleife ist (d.h. sie sind am Ende eines jeden Schleifendurchgangs gültig):
- ) Das Teilarray F[marker+1...n] ist sortiert
- ) Alle Zahlen in F[0...marker] sind nicht größer als jede Zahl in F[marker+1...n]
Damit gilt (nach 1.) auch, dass nach Abbruch der while‐Schleife das Array F[0..n]=F (mit n=F.length‐1) sortiert ist.
Zeige dies durch Induktion nach i=n‐marker:
- i=1: Im ersten Durchgang wird das Maximum as F[0..n] bestimmt und an die letzte Stelle F[n] vertauscht. Damit gilt sowohl 1.) als auch 2.)
- i→i+1: Nehme an, dass nach dem i‐ten Durchgang der while‐Schleife gilt
- ) Das Teilarray F[(i‐n+1)...n] ist sortiert
- ) Alle Zahlen in F[0...(i‐n)] sind nicht größer als jede Zahl in F[(i‐n+1)...n]
Im (i+1) Durchgang wird zunächst das Maximum aus F[0...(i‐n)] bestimmt und anschließend mit dem Element an Position F[i‐n] getauscht. Da nach 2.) dieses Element nicht größer war als jede Zahl in F[(i‐n+1)...n], ist nun F[(i‐n)...n] sortiert (Invariante 1.). Da wir aus F[0...(i‐n)] ein Maximum genommen haben, kann nun auch kein Element in F[0...(i‐n‐1)] größer sein, als jede Zahl in F[(i‐n)...n] (Invariante 2.)
Theorem der Laufzeit
[Bearbeiten]Das Theorem der Laufzeit besagt, dass der Algorithmus SelectionSort eine Laufzeit von hat im besten, mittleren und schlechtesten Fall.
Beweis
[Bearbeiten]Die äußere while‐Schleife wird genau n‐mal (n=F.length) durchlaufen. Dort werden somit n Vertauschungen vorgenommen (=jeweils konstanter Aufwand). Die innere for‐Schleife hat im i‐ten Durchlauf der while‐Schleife n‐i Durchläufe mit jeweils einem Vergleich, deswegen insgesamt
Die Anzahl der Vergleiche ist im besten, mittleren und schlechteste Fall identisch, da immer das komplette Array durchlaufen wird.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.3 zu finden.
BubbleSort
[Bearbeiten]Dieses Kapitel behandelt die Suchmethode BubbleSort. Es handelt sich hierbei um ein sehr bekanntes, aber nicht besonders effizientes Sortierverfahren. Es ist eine einfach zu implementierende zugrunde liegende Vorstellung. Bei einer vertikalen Anordnung von Elementen in Form von Luftblasen (bubbles) werden wie in einer Flüssigkeit von alleine sortiert, da die größeren Blasen die kleiner „überholen“. Das Grundprinzip ist somit die Folge immer wieder zu durchlaufen und dabei benachbarte Elemente, die nicht die gewünschte Sortierreihenfolge haben, zu vertauschen. Das bedeutet Elemente die größer sind als ihre Nachfolger, überholen diese.
Beispiel
[Bearbeiten]Java Code
[Bearbeiten]void BubbleSort(int[] F) {
for (int n= F.length; n >1; n=n-1) {
for (int i =0; i < F.length-1; i++) {
if (F[i] > F[i+1]){
swap(F, i, i+1);
}
}
}
}
Hierbei handelt es sich um die einfachste Form, doch der Algorithmus kann auch optimiert werden. Wir haben beobachtet, dass die größte Zahl in jedem Durchlauf automatisch an das Ende der Liste rutscht. Daraus folgt in jedem Durchlauf j reicht die Untersuchung bis Position n-j, das heißt im j.ten Durchlauf sind die Elemente zwischen den Positionen n-j und n-1 sortiert. Wenn keine Vertauschung mehr stattfindet, soll das Programm abbrechen.
void BubbleSort(int[] F) {
boolean swapped;
int n = F.length;
do {
swapped = false;
for (int i =0; i < n-1; i++) {
if (F[i] > F[i+1]){
swap(F, i, i+1);
swapped = true;
}
}
n--;
}while (swapped);
}
Aufwand
[Bearbeiten]Im besten Fall beträgt der Aufwand n. Im mittleren Fall ohne Optimierung und mit Optimierung . Im schlechtesten Fall ohne Optimierung beträgt der Aufwand und mit Optimierung .
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.4 zu finden.
MergeSort
[Bearbeiten]In diesem Kapitel wird der Sortieralgorithmus MergeSort behandelt.
Rückblick
[Bearbeiten]Die bisherige Verfahren erforderten einen direkten Zugriff auf einzelne Elemente (z.B. in einem Array). Sie sind besonders geeignet für internes Sortieren. Allerdings gibt es Probleme, wenn Daten sortiert werden sollen, die nicht in den den Hauptspeicher passen. Daher brauchen wir andere Verfahren, die nicht zwingend Elemente intern verwalten. Das Prinzip dieser Algorithmen ist das Sortieren in mehreren Phasen oder Schritten.
Idee
[Bearbeiten]MergeSort ist ein Divide-and-Conquer Algorithmus zum vergleichsbasierten Sortieren. Zuerst wird die zu sortierende Folge in zwei Teile geteilt. Anschließend werden beide Teile voneinander getrennt sortiert. Zuletzt werden beide Teilergebnisse in der richtigen Reihenfolge zusammen gemischt.
Beispiel
[Bearbeiten]Algorithmus
[Bearbeiten]void mergeSort(int[] F) {
int[] tmpF = new int[F.length];
mergeSort(F, tmpF, 0, F.length -1);
}
void mergeSort(int[] F, int[] tmpF, int left,int right)
{
if (left < right) {
int m = (left + right)/2;
mergeSort(F, tmpF, left, m);
mergeSort(F, tmpF, m+1, right);
merge(F, tmpF, left, m+1, right);
}
}
void merge(int[] F, int[] tmpF, int startLeft, int startRight, int endRight) {
int endLeft = startRight-1;
int tmpPos = startLeft;
int numElements = endRight – startLeft +1;
while (startLeft <= endLeft && startRight <= endRight)
if (F[startLeft] < F[startRight])
tmpF[tmpPos++] = F[startLeft++];
else
tmpF[tmpPos++] = F[startRight++];
while (startLeft <= endLeft)
tmpF[tmpPos++] = F[startLeft++];
while (startRight <= endRight)
tmpF[tmpPos++] = F[startRight++];
for (int i = 0; i < numElements; i++, endRight--)
F[endRight] = tmpF[endRight];
}
Das Abbruchkriterium für den rekursiven Aufruf ist eine einelementige Liste.Der Misch-Vorgang erfordert in der Regel doppelten Speicherplatz, da eine neue Folge aus den beiden Sortierten generiert werden muss. Eine Alternative ist das Mischen in einem Feld (in-place), das erfordert aber aufwendiges Verschieben.
Analyse
[Bearbeiten]Theorem der Terminierung
[Bearbeiten]Das Theorem der Terminierung besagt, dass der Algorithmus MergeSort für jeden Eingabe int[]F nach endlicher Zeit terminiert.
Beweis
[Bearbeiten]Zeige zunächst, dass jeder Aufruf mergeSort(int[] F, int[] tmpF, int left,int right) terminiert:
- Falls lef < right nicht gilt, terminiert der Aufruf sofort
- Andernfalls rufen wir mergeSort rekursiv auf, wobei entweder lef einen echt größeren oder right einen echt kleineren Wert erhält. In jedem Fall wird nach einem gewissen rekursiven
Abstieg irgendwann lef<right nicht mehr gelten.
Theorem der Korrektheit
[Bearbeiten]Das Theorem der Korrektheit besagt, dass der Algorithmus MergeSort das Problem des vergleichsbasierten Sortierens löst.
Beweis
[Bearbeiten]Durch Induktion nach n = F.length. Annahme n=2 für eine ganze Zahl k.
- n=1: Für n=1 ist der erste Aufruf der mergeSort Hilfsmethode mergeSort(F, tmpF, 0, 0)
und somit gilt nicht lef < right. Die Methode terminiert ohne Änderung an F. Dies ist korrekt, da jedes einelementige Array sortiert ist.
- n/2 → n: Sei F[0...n‐1] ein beliebiges Array. Der erste Aufruf mergeSort(F, tmpF, 0, n-1) erfüllt lef<right und es werden folgende Rekursive Aufrufe getätigt: mergeSort(F, tmpF, 0, n/2-1) mergeSort(F, tmpF, n/2, n-1) Beide Aufrufe erhalten ein Array der Länge n/2. Nach Induktionsannahme gilt, dass anschliessend sowohl F[0...n/2‐1] als auch F[n/2...n‐1] separat sortiert sind. Noch zu zeigen ist, dass merge korrekt zwei sortierte Arrays in ein sortiertes Array mischt.
Theorem der Laufzeit
[Bearbeiten]Das Theorem der Laufzeit besagt, dass der Algorithmus MergeSort eine Laufzeit von hat. Diese Laufzeit ist die selbe für den besten, mittleren und schlechtesten Fall.
Beweis
[Bearbeiten]
Nun wenden wir das Master Theorem an.
Im 2. Fall, wenn
Hier ist a=2 und b=2 und es folgt
Es ist zudem f(n)=n und es gilt für k=0:
Es folgt
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.5 zu finden.
Zwischenbemerkungen
[Bearbeiten]An dieser Stelle gibt es einige Zwischenbemerkungen zu den vorgestellten Sortieralgorithmen.
Einordnung der elementaren Sortierverfahren
[Bearbeiten]| Implementierung Array | Implementierung Liste | |
| greedy | selection sort, bubble sort | insertion sort |
| divide-and-conquer | quicksort | merge sort |
Eigenschaften
[Bearbeiten]Divide and conquer bedeutet teile und herrsche. Dabei wird das eigentliche Problem so lange in kleiner und einfachere Teilprobleme zerlegt, bis man diese lösen kann.Oft können Teilprobleme parallel gelöst werden. Des weiteren sind Teilprobleme „eigenständige“ Probleme. Anschließend werden die Teillösungen zu einer Gesamtlösung zusammengeführt.
Greedy bedeutet gierig. Hierbei wird schrittweise ein Folgezustand ausgewählt, der aktuell den größten Gewinn und das beste Ergebnis verspricht. Die Auswahl des Folgezustands erfolgt anhand von Bewertungsfunktionen und Gewichtsfunktionen. Ein Problem dabei ist, dass oft nur ein lokales Maximum gewählt wird. Mehr dazu im Thema Entwurfsmuster.
Generische Implementierung
[Bearbeiten]Algorithmen werden „parametrisiert“ durch Vergleichsoperator. Im Paket java.lang gibt es dafür ein Interface Comparable. Der Aufruf der Vergleichsmethode a.compareTo(b) liefert ein Zahl <0, =0, >0 für a<b, a=b und a größer b. Das Muster für Objekte vom Referenztyp Comparable lautet:
public class MyObject implements Comparable {
MyType data;
public int compareTo (MyObject obj) {
if („this.data < obj.data“) return -1;
if („this.data = obj.data“) return 0;
if („this.data > obj.data“) return 1;
}
}
Das Muster für Aufrufe in Klassenmethoden bei Suchverfahren lautet:
public static int binarySearch( Comparable[] f,
Comparable a, int l, int r) {
int p = (l+r)/2;
int c = f[p].compareTo(a);
... }
Listenimplementierung generisch
[Bearbeiten]
public class MyObject implements Comparable {. . .}
public class Node {
MyObject data;
Node next;
}
public class OrderedList {
private Node head;
public OrderedList sort ( ) {. . .}
Interne Hilfsmethoden
[Bearbeiten]- int findMin(){...}
- F.findMin() bestimmt den Index des minimalen Elements von OrderedList F
- void insertLast(int a)
- F.insertLast(a) fügt Element mit Index (Key) a an das Ende von F an
- void deleteElem(int a)
- F.deleteElem(a) löscht Element mit Index a aus der Liste F
- Aufwand: jeweils = O(n), wenn n = Anzahl der Objekte in Liste
MergeSort generisch
[Bearbeiten]
public class OrderedList {
OrderedNode head;
int length;
// ...
/** * Sorts this list in non-descending order */
public void mergeSort() {
OrderedList aList, bList; // the divided lists
OrderedNode aChain; // start of first node chain
OrderedNode bChain; // start of second node chain
OrderedNode tmp; // working node for split
// trivial cases
if ( (head==null) || (head.next == null) )
return;
// divide: split the list in two parts
aChain = head;
tmp = head; // init working node for split
// advance half of the list
for (int i=0; i < (length-1) / 2; i++)
tmp=tmp.next;
// cut chain into aChain and bChain
bChain=tmp.next;
tmp.next=null;
// encapsulate the two node chains in two lists
aList = new OrderedList();
aList.head=aChain;
aList.length=length/2;
bList = new OrderedList();
bList.head=bChain;
bList.length=length - aList.length;
// conquer: recursion
aList.mergeSort(); bList.mergeSort();
// join: merge
merge(aList, bList);
}
}
Aus Gründen der Übersichtlichkeit erzeugt dieses Programm im Divide-Schritt jeweils gekapselte Zwischenlisten vom Typ OrderedList. In der Praxis würde man hierauf verzichten und rein auf Knoten-Ketten arbeiten, da insgesamt O(n) Objekte vom Typ OrderedList erzeugt und wieder vernichtet werden(maximal O(log n) davon sind gleichzeitig aktiv).
QuickSort
[Bearbeiten]In diesem Kapitel wird der Sortieralgorithmus QuickSort behandelt.
Idee
[Bearbeiten]Es gibt eine rekursive Aufteilung (wie bei MergeSort), aber hier werden Mischvorgänge vermieden (speicherintensiv!). Die Teillisten werden in zwei Hälften geteilt bezüglich eines Pivot-Elements, wobei in einer Liste alle Elemente größer als das PivotElement sind und in der anderen Liste alle kleiner. Das Pivot Element ist ein beliebiges Element der Liste/Folge, z.B. das linke, mittlere oder rechte Element.
Beispiel
[Bearbeiten]Vertauschen von Elementen
[Bearbeiten]Für gegebenes Pivot-Element p wird die Folge von links durchsuchen, bis das Element gefunden wurde, das größer oder gleich p ist. Und gleichzeitig wird die Folge von rechts durchsuchen, bis das Element gefunden ist, das kleiner p ist. Dabei werden die Elemente ggf. getauscht.
Sortierprinzip
[Bearbeiten]Sortieren einer Folge F[u...o] nach dem „divide-and-conquer“Prinzip. Divide heißt die Folge F[u...o] wird in zwei Teilfolgen F[u...p-1] und F[p+1...o] geteilt. Die zwei Teilfolgen haben folgende Eigenschaften:
- F[i] ≤ F[p] für alle i = u,...,p-1
- F[i] > F[p] für alle i = p+1, …, o
Conquer bedeutet, dass die Teilfolgen sortiert werden. Mit combine werden die Teilfolgen zu F[u...o] verbunden. Vergleiche sind an dieser Stelle nicht erforderlich, da die Teilfolgen bereits sortiert sind.
Pivot Element
[Bearbeiten]Im Prinzip muss man nicht das letzte Element als Pivot‐Element wählen. Je nach Verteilung der Daten, kann es sinnvoll sein ein anderes Element zu wählen. Wenn beispielsweise die Liste schon fast sortiert ist, sollte man immer das mittlere Element wählen Eine optimale Rekursion erhält man, wenn man immer den Median als Pivot-Element wählt (dieser ist aber nicht direkt bestimmbar, dafür müsste man die Liste erst sortiert haben. Hat man ein Pivot-Element ausgewählt, tauscht man dies einfach mit dem letzten Element und benutzt den Algorithmus wie zuvor.
Algorithmus
[Bearbeiten]void quickSort(int[] F, int u, int o) {
if (u < o) {
int p = (u+o)/2;
int pn = zerlege(F,u,o,p);
quickSort(F,u,pn-1);
quickSort(F,pn+1,o);
}
int zerlege(int[] F, int u, int o, int p) {
int pivot = F[p];
int i = u;
int j = o;
while (i < j) {
while (F[i] < pivot)
i++;
while (F[j] > pivot)
j--;
if (i < j) {
swap(F,i , j );
}
}
return i;
}
int zerlege(int[] F, int u, int o, int p) {
int pivot = F[p];
//Tausche Pivot-Element mit dem letzten Element
//kann entfallen, wenn immer p=o gewählt wird
swap(F,p, o);
int pn = u;
//bringe kleinere Elemente nach vorne und größere nach hinten
for (int j = u; j < o; j++) {
if (F[j] <= pivot){
swap(F,pn, j );
pn++;
}
}
//bringe das Pivot-Element an die richtige Position und gebe diese zurück
swap(F,pn, o);
return pn;
}
void swap(int[] f, int x, int y){ //Hilfsmethode zum Vertaucshen
int tmp = f[x];
f[x] = f[y];
f[y] = tmp;
}
}
P gibt an ,an welcher Position das Pivot Element ist. Bei diesem Beispiel ist es in der Mitte. Es kann aber auch an Stelle o oder u sein.
Beispiel 1
[Bearbeiten]Zerlege (F,0,6,3) mit 3=(0+6)/2
| 8 | 2 | 1 | 5 | 9 | 7 | 3 |
...
| 3 | 2 | 1 | 5 | 9 | 7 | 3 |
Beispiel 2
[Bearbeiten]Sei f[8]=5 das Pivot-Element
| 8 | 9 | 2 | 6 | 7 | 3 | 4 | 1 | 5 |
Suche von links aus das Element, welches kleiner als das Pivot-Element ist
| 8 | 9 | 2 | 6 | 7 | 3 | 4 | 1 | 5 |
Vertausche mit dem ersten größeren Element
| 2 | 9 | 8 | 6 | 7 | 3 | 4 | 1 | 5 |
Suche das nächste kleinere Element als die 5
| 2 | 9 | 8 | 6 | 7 | 3 | 4 | 1 | 5 |
Vertausche dieses mit dem zweiten größeren Element
| 2 | 3 | 8 | 6 | 7 | 9 | 4 | 1 | 5 |
Suche wieder das nächste kleinere Element
| 2 | 3 | 8 | 6 | 7 | 9 | 4 | 1 | 5 |
und vertausche dies mit dem dritt größeren Element
| 2 | 3 | 4 | 6 | 7 | 9 | 8 | 1 | 5 |
| 2 | 3 | 4 | 6 | 7 | 9 | 8 | 1 | 5 |
| 2 | 3 | 4 | 1 | 7 | 9 | 8 | 6 | 5 |
nun ist man rechts angekommen und hier wird nun das Pivot-Element getauscht
| 2 | 3 | 4 | 1 | 5 | 9 | 8 | 6 | 7 |
Von nun an steht das Pivot-Element an seiner finalen Position. Alle Elemente links vom Pivot-Element sind kleiner und alle auf der rechten Seite sind größer. Das bedeutet, dass nun ein rekursiver Abstieg für die Folgen
| 2 | 3 | 4 | 1 |
und
| 9 | 8 | 6 | 7 |
beginnen würde. Wenn das letzte Element wieder als Pivot-Element gewählt werden würde, dann hat die erste erste Folge nun das Pivot-Element 1 und in der zweiten Folge währe es das Element 7.
Alternative: Zerlegung mit while-schleifen
[Bearbeiten]Man wählt zuerst ein Pivotelement, beispielsweise das mittlere Element. Nun beginnt man von unten an und vergleicht die Einträge mit dem Pivot. Danach beginnt man von oben und vergleicht die Elemente mit dem Pivot. Wenn ein Element kleiner bzw. größer ist als das Pivot Element, dann wird dieses Element getauscht.
Analyse
[Bearbeiten]Theorem der Terminierung
[Bearbeiten]Das Theorem der Terminierung besagt, dass der Algorithmus quickSort für jede Eingabe int[]F nach endlicher Zeit terminiert.
Beweis
[Bearbeiten]In jedem rekursiven Aufruf von quickSort ist die Eingabelänge um mindestens 1 kleiner als vorher und die Rekursionsanfang ist erreicht wenn die Länge gleich 1 ist. In der Methode split gibt es nur eine for‐Schleife, dessen Zähler j in jedem Durchgang inkrementiert wird. Da u<o wird die for‐Schleife also nur endlich oft durchlaufen.
Theorem der Korrektheit
[Bearbeiten]Das Theorem der Korrektheit besagt, dass der Algorithmus quickSort das Problem des vergleichsbasierten Sortierend löst.
Beweis
[Bearbeiten]Die Korrektheit der Methode swap ist zunächst offensichtlich. Zeige nun, dass nach Aufruf pn=split(f,u,o,p) für u<o und gilt:
- f[p] wurde zu f[pn] verschoben
Dies ist klar (vorletzte Zeile der Methode split)
- f[i] ≤ f[pn] für i=u,...,pn‐1
pn wird zu anfangs mit u initialisiert und immer dann inkrementiert, wenn die Position f[pn] durch ein Element, das kleiner/gleich dem Pivot‐Element ist, belegt wird.
- f[i] > f[pn] für i=pn+1,...,o
Folgt aus der Beobachtung, dass in 2.) immer „genau dann“gilt. Beachte zudem, dass Element immer getauscht werden, also die Elemente im Array stets dieselben bleiben.
Die Korrektheit der Methode quickSort folgt nach Induktion nach der Länge von f (n=f.length):
- n=1: Der Algorithmus terminiert sofort und ein einelementiges Array ist stets sortiert
- n→n+1: Nach Korrektheit von split steht das Pivot‐Element an der richtigen Stelle und links und rechts stehen jeweils nur kleinere/größere Element. Die beiden rekursiven Aufrufe von quickSort erhalten jeweils ein Array, das echt kleiner als n+1 ist (mindestens das Pivot‐Element ist nicht mehr Teil des übergebenen Arrays). Nach Induktionsannahme folgt die Korrektheit von quickSort.
Theorem der Laufzeit
[Bearbeiten]Das Theorem der Laufzeit besagt, dass wenn als Pivot Element stets der Median des aktuell betrachteten Arrays gewählt wird, so hat der Algorithmus quickSort eine Laufzeit von .
Beweis
[Bearbeiten]Es gilt zunächst, dass split . Ausschlaggebend ist hier die for-Schleife, die genau n-mal durchlaufen wird. Gilt nach dem Aufruf von split stets pn=(u+o)/2 (dies ist gleichbedeutend damit, dass das Pivot‐Element stets der Median ist), so erhalten wir folgende Rekursionsgleichung für quickSort:
Die ist fast dieselbe Rekursionsgleichung wie für MergeSort und es folgt
Doch was ist, wenn die Voraussetzung des Theorems nicht erfüllt ist und wir ungleiche Rekursionsaufrufe haben?
Theorem der Laufzeit 2
[Bearbeiten]Das Theorem der Laufzeit besagt, dass der Algorithmus quickSort im schlechtesten Fall eine Laufzeit von hat.
Beweis
[Bearbeiten]Angenommen, die Aufteilung erzeugt ein Teilarray mit Länge n‐1 und ein Teilarray mit Länge 0 (Pivot‐Element ist also immer Minimum oder Maximum), dann erhalten wir folgende Rekursionsgleichung für die Laufzeit:
Durch Induktionsbeweis kann leicht gezeigt werden, dass . Dies ist auch tatsächlich der schlechteste Fall.
Für den mittleren Fall kann gezeigt werden, dass quickSort einen Aufwand von hat (wie im besten Fall), die in versteckten Konstanten sind nur etwas größer.
Bemerkung
[Bearbeiten]Im Gegensatz zu MergeSort ist QuickSort durch die Vorgehensweise bei Vertauschungen instabil, d.h. relative Reihenfolge gleicher Schlüssel werden nicht notwendigerweise beibehalten.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.6 zu finden.
Heap Sort
[Bearbeiten]Auf dieser Seite wird das Thema Heap Sort behandelt. Von "Heap" gibt es zwei völlig verschiedene Definitionen. Zum einen ist es ein größeres Gebiet im Hauptspeicher, aus dem Programmierer Blöcke beanspruchen und wieder freigeben können und zum anderen ist es ein balancierter, linksbündiger Binärbaum in dem kein Knoten einen Wert hat, der größer ist als der Wert seines Elternknoten. Im Falle von Heapsort wird die zweite Definition benutzt.
Balancierter Binärbaum
[Bearbeiten]Jeder Knoten ist in einer Ebene platziert, der Wurzelknoten in Ebene 0. Die Höhe eines Baumes ist die Distanz von seiner Wurzel zum weitest entfernten Knoten plus 1. Ein Knoten ist tiefer als ein anderer Knoten, wenn seine Ebene eine höhere Zahl hat. Ein Binärbaum der Höhe h ist balanciert, wenn alle Knoten der Ebenen 0 bis h-3 zwei Kinder haben.
Ein balancierter Binärbaum der Höhe h ist linksbündig, wenn er Knoten in der Ebene k hat für alle und alle Blätter der Ebene h-1 so weit wie möglich links sind.
Motivation
[Bearbeiten]Der Vorteil von MergeSort gegenüber QuickSort ist, dass MergeSort einen garantierten Aufwand von O(n log n) hat. Der Vorteil von QuickSort gegenüber MergeSort ist, dass QuickSort n viel Speicher benötigt und MergeSort 2n viel Speicher. Gibt es nun einen Sortieralgorithmus, der n viel Speicher benötigt und garantiert in O(n log n) läuft? Ja HeapSort! Mit HeapSort lassen sich zudem die Warteschlangen mit Prioritäten effizient implementieren. Außerdem ist die Idee des Heaps sehr interessant. Eine komplexe Datenstruktur (Baum) wird in einer einfacheren Struktur (Array) abgebildet.
Heap Eigenschaft
[Bearbeiten]Ein Knoten hat die Heap-Eigenschaft, wenn der Wert in dem Knoten so groß oder größer ist als die Werte seiner Kinder. Alle Blattknoten haben dann auch automatisch die Heap Eigenschaft. Ein Binärbaum ist nur dann ein Heap, wenn alle Knoten die Heap Eigenschaft besitzen.
Anmerkung
[Bearbeiten]Ein Heap ist kein binärer Suchbaum. Das Sortierkriterium bei Suchbäumen war, dass der Wert eines Knotens stets größer ist, als die Werte der Knoten, die im linken Teilbaum liegen und, dass der Wert eines Knotens stets kleiner ist, als die Werte der Knoten, die im rechten Teilbaum liegen. Das Sortierkriterium beim Heap ist, dass die Werte eines Knotens stets größer oder gleich der Werte der Knoten sind, die in beiden Teilbäumen liegen.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.6.1 zu finden.
Untere Schranke
[Bearbeiten]Auf dieser Seite wird die untere Schranke für vergleichbare Sortierverfahren behandelt.
Eigenschaften der betrachteten Algorithmen
[Bearbeiten]Die Komplexität im Durchschnittsfall und im Schlechtesten Fall ist nie besser als n ‧ log n. Die Sortierung erfolgt ausschließlich durch Vergleich der Eingabe-Elemente (comparison sorts), es handelt sich somit um vergleichsorientierte Sortierverfahren. Nun zeigen wir, dass n ‧ log n Vergleiche eine untere Schranke für „Comparison Sort“-Algorithmen ist. Dies heißt dann, dass Sortieralgorithmen mit Komplexität (schlechtester Fall) von n ‧ log n (z.B. MergeSort) asymptotisch optimal sind.
Problembeschreibung
[Bearbeiten]Zuerst die Problembeschreibung. Als Eingabe haben wir . Als Vergleichstests nehmen wir . Als vereinfachte Annahmen nehmen wir an, dass es nur verschiedene Elemente gibt, somit entfällt . Die restlichen Test liefern alle gleichwertige Informationen. Sie bestimmen die Reihenfolge von . Außerdem können sie und auf beschränken. Somit haben wir eine binäre Entscheidung und es gilt entweder
Entscheidungsbaum
[Bearbeiten]
Eine beispielhafte Eingabe ist Die inneren Knoten vergleichen die Elemente . Es wird ein Test durchgeführt ob gilt oder nicht. Die Blätter sind Permutationen mit Sortieren heißt das Finden eines Pfades von der Wurzel zu einem Blatt. An jedem internen Knoten erfolgt ein Vergleich und entsprechend wird links oder rechts weiter gesucht. Ist ein Blatt erreicht, dann hat der Sortieralgorithmus eine Ordnung und die Permutation der Elemente ist erstellt. Daraus lässt sich schlussfolgern, dass jeder Sortieralgorithmus jede Permutation der n Eingabe-Elemente erreichen muss (n!). Daraus folgt wiederum, dass es n! Blätter geben muss, die alle von der Wurzel erreichbar sind. Andernfalls kann er zwei unterschiedliche Eingaben nicht unterscheiden und liefert für beide dasselbe Ergebnis und eins davon muss falsch klassifiziert sein. Die Anzahl an Vergleichen im schlechtesten Fall ist die Pfadlänge von Wurzel bis Blatt, oder auch Höhe genannt.
Somit erhalten wir das Theorem, dass jeder vergleichsorientierte Sortieralgorithmus im schlechtesten Fall mindestens n*log n Versuche braucht.
Beweis
[Bearbeiten]Gegeben ist die Anzahl der Elemente n, h die Pfadlänge bzw. Höhe des Baums und b die Anzahl der Blätter. Jede Permutation muss in einem Blatt sein, das bedeutet . Der Binärbaum hat die Höhe h und maximal Blätter, daraus folgt . Wenn man nun logarithmiert, erhält man
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 5.2.7 zu finden.
Listen
[Bearbeiten]Abstrakter Datentyp
[Bearbeiten]ADT bedeutet abstrakter Datentyp. Man fasst Daten und Operationen auf ihnen in einem ADT zusammen. Dieses Konzept ist von der objektorientieren Programmierung bekannt. Ein ADT entspricht hier einer Klasse, welche die Operationen implementiert, die auf einer Datenstruktur ausgeführt werden können. Die Operationen entsprechen hier dem Interface. Die Datentypen, die wir in dieser Vorlesung behandeln werden, sind in der Java Collection API bereits konkret implementiert. Die Collection API bietet diese Operationen über Interfaces an. So gibt es ein Interface List für Listen, ein Interface Set für Mengen und ein Interface Map für die Zuordnung zwischen Schlüsseln und zugehörigen Werten. Die eigentliche Datenstruktur ist dabei die Implementierung in einer Klasse. Die Idee ist demnach, dass wir durch die Definition eines Interfaces Operationen vorgeben und verschiedene Implementierungen von Datentypen realisieren können, welche unterschiedliche Aspekte beleuchten. Wir werden heute die Operationen für eine Liste sehen. Dann werden wir unterschiedliche Arten von Listen kennenlernen, welche diese Operationen implementieren.
ADT abstrakter Datentyp
Daten und Operationen auf dem ADT gehören zusammen
Generell kann man, wie aus der Collection API bereits bekannt, in jeder Speicherstruktur jeden beliebigen Datentypen verwalten. Wir werden hier der Einfachheit halber jeweils nur Integer Werte in den Datenstrukturen ablegen. Man kann jedoch wegen der in Java verwendeten generischen Implementierung der Datenstrukturen beliebige Objekte typensicher in ihnen ablegen. Betrachten wir nun die Datentyp Liste:
Einfach verkettete Listen
[Bearbeiten]ADT Liste: Ggfs. leere Sequenz von Elementen
Die Elemente einer Liste bezeichnet man häufig als Knoten. Jedes Element zeigt dabei auf das ihm nachfolgende Element. Der Zeiger im letzten Element zeigt auf null. Die folgende Abbildung illustriert diese Verkettung. Ein Element besteht demnach aus einem Feld data, welches die Nutzdaten (in unserem Falle Integer) enthält und einem Feld next, welches einen Zeiger auf das folgende Element enthält. Um die Datenstruktur verwenden zu können, gibt es noch einen Zeiger auf das erste Element der Liste, welcher üblicherweise mit head bezeichnet wird.

Hinweis für die Übungsaufgaben: Es empfiehlt sich immer, die betrachtete Situation als Bild zu zeichnen und sich anhand dessen zu überlegen, welche Fälle und Sonderfälle auftreten können und in welcher Reihenfolge welche Operationen nun notwendig sind.
Durch Zuweisungen an den Zeiger next wird die innere Struktur der Liste geändert. Falls dies in der falschen Reihenfolge geschieht, werden Teile der Liste "abgehängt" und sind nicht mehr erreichbar.
Operationen auf Listen
[Bearbeiten]Auf einfach Listen haben wir folgenden Operationen:
- isEmpty(L)
- size(L)
- find(x, L)
- get(pos, L)
- insert(x, L)
- insertPos(x, pos, l)
- append(x, L)
- remove(x, L)
Ist die Liste leer ?
[Bearbeiten]Die Operation isEmpty ist sehr leicht zu implementieren, da wir lediglich prüfen müssen, ob der head Zeiger null ist. Diese Operation hat eine Laufzeit von .
isEmpty(L)
return L.head = null
Größe bestimmen
[Bearbeiten]Um für eine beliebige Liste die Länge der Liste zu bestimmen, müssen wir einmal durch die komplette Liste laufen. Wir benötigen eine Variable count, welche wir mit 0 initialisieren. Weiterhin brauchen wir einen Zeiger tmp auf das Element der Liste, welches wir gerade bearbeiten. Dieser verweist zum Programmstart auf das Element head der Liste. Der Algorithmus ended, sobald wir mit dem Zeiger tmp auf null zeigen. Im Rumpf der Schleife müssen wir den tmp Zeiger immer um einen Konten weiterrücken (tmp = tmp.next) und außerdem die Variable count um eins nach oben Zählen. Schließlich geben wir den Wert von count zurück.

size(L)
count := 0
tmp := L.head
while tmp ≠ null
tmp := tmp.next
count := count + 1
return count
Element suchen
[Bearbeiten]find liefert entweder den Knoten, bei dem das Feld data den Wert x hat oder falls kein solcher Knoten vorhanden ist, den Wert null zurück. Für die leere Liste ist der Rückgabewert null. Andernfalls müssen wir wieder die Liste mit einem Zeiger tmp durchlaufen, welchen wir am Anfang auf den Wert von head setzen. Solange das data Feld des Zeigers tmp nicht den Wert x enthält und wir noch nicht am Ende der Liste angekommen sind gehen wir die Liste durch tmp := tmp.next. Anschließend prüfen wir, ob das data Feld des Zeigers tmp den Wert x hat und geben in diesem Fall tmp zurück, andernfalls geben wir null zurück.
find(x, L)
if not isEmpty(L)
tmp := L.head
while tmp.next ≠ null and tmp.data ≠ x
tmp := tmp.next
if tmp.data = x
return tmp
return null

Wir nehmen an, x liege auf dem dritten Knoten. Wir stellen fest, dass die Liste nicht leer ist und setzten daher den Zeiger tmp auf den Wert von head. Somit zeigt tmp nun auf das erste Element. Nun prüfen wir, ob wir weiterrücken dürfen und stellen fest, dass der next Zeiger einen von null verschiedenen Wert hat und das Feld data einen Wert ungleich x aufweist. Somit rücken wir, wie im Körper der while Schleife vorgesehen, weiter zum zweiten Element der Liste. Dort führen wir selbige zwei Prüfungen erneut durch. Wieder stellen wir fest, dass sowohl der next Zeiger einen Wert ungleich null besitzt, als auch das im Feld data ein von x verschiedener Wert vorhanden ist und rücken erneutet den Zeiger tmp um ein Element vor, so dass er nun auf das dritte Element der Liste verweist. Hier stellen wir fest, dass im Feld data nun der Wert x vorhanden ist und verlassen daher die Schleife. Nun überprüfen wir entsprechend der if Bedingung, ob wir das Element x gefunden haben und geben somit den gefundenen Knoten tmp als Ergebnis zurück.
Element einfügen
[Bearbeiten]In der folgenden Abbildung sehen wir ein neues Element x, welches wir in eines Liste einfügen wollen.

Wir fügen das Element am Anfang der Liste ein, da wir dann keinen Aufwand zum Suchen der Einfügestelle haben und die Aufgabe in lösen können. Zunächst setzen wir den Zeiger für den Nachfolger im Knoten des neu einzufügenden Elements auf den derzeitigen Wert von head. Anschließend sorgen wir dafür, dass head auf den neu eingefügten Knoten zeigt.
insert(x, L)
node := newNode(x)
if not isEmpty(L)
node.next = head
L.head := node
Bei der leeren Liste müssen wir lediglich den Zeiger head auf den neu anzulegenden Knoten verbiegen. Legen wir also zunächst einen neuen Knoten an node := newNode(x). Nun müssen wir schauen, ob die Liste nicht leer ist: not isEmpty(L). In diesem Fall (Liste ist nicht leer) müssen wir zunächst dem Nachfolgerzeiger des neu angelegten Knotens den Wert von head zuweisen: node.next = head. Anschließend müssen wir unabhängig davon, ob die Liste ursprünglich leer war, den head Zeiger der Liste auf den neu angelegten Knoten verbiegen: L.head := node.
Element an bestimmter Postion einfügen
[Bearbeiten]
Wir wollen nun ein neues Element x an Position zwei einfügen. Daher verbiegen wir zunächst den Nachfolgerzeiger des neuen Knotens auf den bisherigen zweiten Knoten und erst anschließend im zweiten Schritt den Nachfolgerzeiger des ersten Knotens auf den neu eingefügten Knoten.
insertPos(x, pos, L)
if isEmpty(L)
insert(x, L)
else
tmp := L.head
i := 0
while tmp.next ≠ null and i < pos - 1
tmp := tmp.next
i := i + 1
node := newNode(x)
node.next := tmp.next
tmp.next := node
Im Falle der nicht leeren Liste müssen wir die Liste auf der Suche nach der gewünschten Einfügeposition durchsuchen. Wir benötigen also einen temporären Zeiger tmp, welchen wir zuerst auf den Anfang der Liste setzten tmp := L.head. Weiterhin benötigen wir einen Integer i, um die Position in der Liste, an der wir uns aktuell befinden, zu verwalten. Wir initialisieren i mit dem Wert 0, da das Element am Kopf der Liste der Position 0 entspricht. Nun durchlaufen wir die Liste mit einer while Schleife. Haben wir das Ende der Liste noch nicht erreicht, hat entsprechend der next Zeiger des Knotens tmp einen von null verschiedenen Wert (tmp.next ≠ null), so können wir weiterrücken, sofern wir die gewünschte Einfügeposition noch nicht erreicht haben. Die folgende Abbildung illustriert die Situation beim Erreichen der gewünschten Einfügeposition während des Durchlaufs der while Schleife:

In der Abbildung zeigt der Zeiger tmp auf das erste Element. Hier können wir die Einfügeoperation vornehmen, weil wir hier Zugriff auf den next Zeiger des ersten Knotens haben, welchen wir auf das neu einzufügende Element verbiegen müssen. In diesem Fall gilt gerade i = pos - 1. Somit dürfen wir, um den Fall des Erreichens der Einfügeposition zu berücksichtigen, in der while Schleife nur vorrücken, falls zusätzlich die Bedingung i < pos - 1gilt. Im Körper der while Schleife müssen wir nun den tmp Zeiger auf das folgende Element vorrücken tmp := tmp.next. Außerdem müssen wir den Zähler i im Körper der while Schleife inkrementieren i := i + 1. Nach Durchlauf dieser Schleife wurde entweder die korrekte Einfügeposition gefunden und tmp zeigt auf das Element, dessen next Zeiger wir auf das neue Element verbiegen wollen, oder der Zeiger tmp zeigt auf den letzten Knoten der Liste. Wir müssen also in beiden Fällen einen Knoten für das neue Element anlegen node := newNode(x) und den Nachfolgerzeiger next des Knotens tmp auf den Knoten des neu einzufügenden Elements verbiegen: tmp.next := node. Außerdem müssen wir den Nachfolgerzeiger des neu erstellten Knotens festlegen. Somit können wir in beiden Fällen dem Nachfolgerzeiger des neu einzufügenden Knotens den Wert des Nachfolgerzeigers des Knotens tmp zuweisen node.next := tmp.next.
Element nach Index suchen
[Bearbeiten]Wir initialisierten zunächst den Positionszähler i mit 0. Weiterhin setzen wir den Zeiger zum Durchlauf der Elemente tmp auf den Anfang der Liste tmp := L.head. Nun müssen wir die Schleifenbedingung der while Schleife festlegen. Hierzu stellen wir die Situation in der folgenden Abbildung graphisch dar.

Nehmen wir an, wir wollten das zweite Element der Liste bestimmen. Da wir tmp zurückliefern wollen, müssen wir in der Schleifenbedingung, im Unterschied zum oben beim Einfügen behandelten Fall, prüfen, ob der Zeiger tmp nicht den Wert null hat tmp ≠ nullund ob wir den gewünschten Index bereits erreicht haben i < pos. Im Körper der Schleife müssen wir genauso wie vom oben beschriebenen Einfügen her bekannt, den Zeiger auf das nächste Element weiterrücken tmp := tmp.next und den Elementzähler um eins erhöhen i := i + 1. Im Falle i = pos haben wir entweder das gesuchte Element gefunden oder wir haben das Ende der Liste erreicht und tmp verweist auf null. In beiden Fällen erreichen wir durch Rückgabe von tmp das gewünschte Ergebnis.
get(pos , L)
if not isEmpty(L)
tmp := L.head
i := 0
while tmp ≠ null and i < pos
tmp := tmp.next
i := i + 1
if i = pos
return tmp
return null
Element hinten anfügen
[Bearbeiten]Mit size können wir die Länge der Liste bestimmen und mit insertPos an einer frei wählbaren Stelle in die Liste einfügen. Wir wählen size(L) als Einfügepositon und fügen somit am Ende der Liste ein. Die Funktion size benötigt Schritte. Die Funktion insertPos benötigt ebenfalls Schritte. Somit benötigen wir insgesamt Schritte. Unser Verfahren hat demnach eine Laufzeit von .
append(x, L)
insertPos(x, size(L), L)
Es gibt eine alternative Implementierung, welche das Problem in Schritten löst:
append2(x, L)
tmp := L.head
while tmp.next ≠ null
tmp := tmp.next
tmp.next = newNode(x)
Element entfernen
[Bearbeiten]
Wir müssen den Zeiger tmp bis auf das Element vor dem gesuchten Element vorrücken und können anschließend dessen Nachfolgerzeiger next wie in der Abbildung dargestellt auf das Element verbiegen, welches dem gesuchten Element nachfolgt. Wir müssen noch zwei weitere Spezialfälle behandeln. Zum einen kann die Liste ausschließlich aus einem einzigen Element bestehen.

In diesem Fall genügt es, dem Kopfzeiger der Liste head den Wert null zuzuweisen. Zum anderen kann es passieren, dass die Liste mindestens zwei Elemente enthält und wir das erste Element der Liste (das ist das Element auf den der Kopfzeiger head verweist) aus der Liste entfernen wollen. Die folgende Abbildung zeigt diese Situation.

In diesem Fall müssen wir den Kopfzeiger head um eine Position weiterrücken, so dass er dann auf den Nachfolger des zu entfernenden Elementes verweist head := head.next. Wir schreiben somit diese Anweisung in den Rumpf der Bedingung if L.head.data = x. Andernfalls müssen wir den Standardfall behandeln und die Liste mit einer while Schleife durchsuchen. Wir wollen die while Schleife solange durchlaufen, wie wir entweder das gesuchte Element noch nicht erreicht haben tmp.next.data ≠ x, oder noch nicht am Ende der Liste angekommen sind tmp.next ≠ null. Im Rumpf der while Schleife rücken wir den Zeiger tmp auf das jeweils folgende Element vor tmp := tmp.next.
Entsprechend prüfen wir, ob wir das gesuchte Element gefunden haben if tmp.data = x. In diesem Fall müssen wir den Nachfolgerzeiger des Elements auf das tmp zeigt um ein Element auf den Übernächsten weiterrücken tmp.next = tmp.next.next.
remove(x, L)
if not isEmpty(L)
if L.head.data = x
L.head:=L.head.next
else
tmp:=L.head
while tmp.next ≠ null and tmp.next.data ≠ x
tmp := tmp.next
if tmp.next.data != null
tmp.next := tmp.next.next
Kreis finden
[Bearbeiten]In der folgenden Abbildung sehen wir eine Liste, in der der Nachfolgerzeiger des letzten Elementes nicht den Wert null hat, sondern auf ein Element der Liste verweist. Wir sagen in diesem Falle auch: Die Liste enthält einen Kreis.

Daher ist es sinnvoll ein Verfahren zu haben, mit dem man feststellen kann, ob eine Liste einen Kreis enthält. Eine gute Lösung bietet hier der Hase und Igel Algorithmus. Hierfür setzen wir einen Zeiger auf das erste Element der Liste, welchen wir als Igel bezeichnen. Weiterhin setzen wir einen Zeiger auf das zweite Element der Liste, welchen wir als Hasen bezeichnen. Wir lassen in jedem Schritt den Igel um ein Element vorrücken, jedoch gleichzeitig den Hasen um zwei Elemente. Enthält die Liste keinen Kreis, so erreicht der Hase nach endlich vielen Schritten das Ende der Liste. Enthält die Liste jedoch einen Kreis, so holt der Hase irgendwann den Igel ein. Man sieht, dass der Algorithmus nach bereits zwei Schritten terminiert, weil dann sowohl der Hase als auch der Igel auf das Element, welches die Zahl 3 enthält, verweisen.
hasCircle(L):
if isEmpty(L) or L.head.next = null
return false
igel := L.head
hase := L.head.next
while hase.next ≠ null
if hase = igel
return true
if hase.next.next = null
return false
hase := hase.next.next
igel := igel.next
return false
Im Falle der leeren Liste isEmpty(L), sowie im Falle der einelementigen Liste, deren einziges Element einen Nachfolgerzeiger mit dem Wert null enthält (L.head.next = null), gibt es keinen Kreis. In diesem Falle geben wir false zurück. Andernfalls setzten wir den Igel auf das erste Element der Liste igel := L.head und den Hasen auf das zweite Element der Liste hase := L.head.next. Nun müssen wir eine while Schleife durchlaufen, solange der Nachfolgezeiger des Hasen einen Wert ungleich null besitzt hase.next ≠ null. Im Rumpf der while Schleife prüfen wir mit einer if Bedingung, ob wir einen Kreis gefunden haben hase = igel und geben in diesem Fall dies als Ergebnis zurück return true.
Es kann jedoch auch vorkommen, dass der Hase nicht sinnvoll weiterspringen kann, weil der übernächste Nachfolger des Hasen den Wert null besitzt. Daher müssen wir diesen Fall ebenfalls im Rumpf der while Schleife mit einer if Bedingung behandeln hase.next.next = null. In diesem Falle geben wir zurück, dass die Liste keinen Kreis besitzt return false. Schließlich müssen wir ebenfalls noch im Rumpf der while Schleife den Sprung des Hasen hase := hase.next.next sowie den Sprung des Igels igel := igel.next ausführen.
Schließlich geben wir, sofern die Schleife verlassen wurde, zurück, dass die Liste keinen Kreis enthält return false.
Doppelt verkettete Liste
[Bearbeiten]Wir haben nun gesehen, dass die oben behandelten elementaren Operationen auf einer einfach verketten Liste einen hohen Rechenaufwand aufweisen. Nehmen wir beispielweise an, wir wollten eine einfach verkette Liste sortieren. Wir haben bisher gesehen, dass wir in jedem Einzelschritt jedes Sortierverfahrens, je zwei Elemente vertauschen. Es ist also interessant das Laufzeitverhalten der einfach verketteten Liste für den Tausch zweier Elemente zu untersuchen. Nehmen wir an, wir hätten zwei Zeiger auf die Elemente in der Liste, welche wir vertauschen wollen. Wir benötigen jedoch die jeweiligen Vorgänger der Elemente um deren Nachfolgerzeiger verbiegen zu können. Diese Situation ist in der folgenden Abbildung dargestellt.

Hierdurch entsteht ein erheblicher Laufzeitaufwand, da wir die Liste vom Kopf angefangen bis zu den jeweiligen Vorgängerelementen durchlaufen müssen. Es entsteht daher ein Aufwand . Eine Lösung bietet hier die doppelt verkettete Liste. Jedes Element der doppelt verketteten Listen enhält zusätzlich zu dem von der einfach verketteten Liste bereits bekannten Nachfolgerzeiger next auch einen Zeiger auf den Vorgänger prev. Durch die Verfügbarkeit eines Zeiger auf das vorausgehende Element können wir nun in konstanter Zeit zwei Elemente tauschen. Mehr hierzu werden wir in den Übungsaufgaben besprechen. Die folgende Abbildung zeigt ein Beispiel einer doppelt verketteten Liste.

insertionSort
[Bearbeiten]Es gibt Anwendungsfälle in denen sortiere Listen verwendet werden. Sortieren ist eine der Informatik häufig zu lösende Aufgabe. Wir haben bereits einige Verfahren zum Sortieren von Arrays kennen gelernt. Arrays haben jedoch den Nachteil, dass sie eine festgelegte Größe besitzen und eine Änderung der Größe ein Umkopieren des Arrays erfordert, welches einen hohen Rechenaufwand mit sich bringt. Daher möchte man auch eine Liste sortieren können. Hierzu bietet sich InsertionSort als geeignetes Verfahren an. Man fügt einfach jedes Element an der richtigen Stelle ein. Man beginnt demnach mit einer leeren Liste. Anschließend fügt man die Elemente nacheinander jeweils richtig ein. In einem Array wäre dieses Verfahren schwer Praktikabel weil das Einfügen zwischen zwei vorhandenen Elementen eine erheblichen Kopieraufwand zum Verschieben der bereits vorhandenen Elemente mit sich brächte. In der folgenden Abbildung sehen wir eine sortierte Liste mit den Einträgen 5, 9, 12 und 17. In diese Liste wollen wir die Zahl 13 einfügen.

Hierzu müssen wir den Knoten in der Liste mit dem größten Wert, welcher gerade noch kleiner ist als 13 finden und anschließend die Zeiger entsprechend verbiegen. Der zu entfernende Zeiger ist in der Abbildung als gepunktete Linie angedeutet. Die neu einzufügenden Zeiger sind als gestrichelte Linien dargestellt. Bei diesem Verfahren haben wir immer eine sortierte Liste. Bei jedem Einfügevorgang wird darauf geachtet, dass die Sortiertheit der Liste erhalten bleibt. In der Java Collection API gibt es die Klasse SortedList, welche genau dieses Verfahren implementiert. Schauen wir uns nun die Implementierung des Verfahrens an.
insertSorted(x, L)
if isEmpty(L)
insert(x, L)
else
while tmp.next ≠ null and tmp.next.data < x
tmp := tmp.next
node := new(x)
node.next := tmp.next
tmp.next := node
Skip Listen
[Bearbeiten]Stack
[Bearbeiten]Stack
[Bearbeiten]Im Gegensatz zur Liste ist der Stack eine international standardisierte Datenstruktur.
ADT Stack: ggf. leere Folge von Elementen zusammen mit einem ggf. undefinierten Topelement
Bei einem Stack hat man jeweils nur Zugriff auf das oberste Element. Man kann dieses inspizieren oder entfernen. Ferner kann man ein neues Element auflegen. Womit das bisherige oberste Element erst einmal nicht mehr erreichbar ist. Nimmt man das neu aufgelegte Element jedoch wieder vom Stack herunter, so hat man wieder Zugriff auf das alte oberste Element.
| | |X| ← Oberstes Element: - inspizieren |X| - auflegen |X| - entfernen |X| ---
Beim Entfernen wird lediglich das Element vom Stack entfernt. Dieses wird jedoch nicht zurückgegeben. Bei Inspizieren wird das oberste Element zurückgegeben, es bleibt jedoch als oberstes Element auf den Stack und wir nicht etwa von diesem entfernt.
Auf einen Stack haben wir folgende Operationen:
- newStack() Stack
- push(x, s) Stack
- pop(s) Stack
- top(s) Element
- isEmpty(s) boolean
Durch die folgenden vier Axiome ist ein Stack eindeutig definiert. Wir nennen sie daher Stackaxiome:
- s:Stack
- x:Element
- (A1) isEmpty(newStack()) = true
- (A2) isEmpty(push(x, s)) = false
- (A3) top(push(x, s)) = x
- (A4) pop(push(x, s)) = s
Stacks lassen sich sowohl mit Hilfe von Arrays als auch mit Hilfe von Listen implementieren. Bei der Implementierung mit einem Array, muss das Array, sobald es vollständig gefüllt ist und ein weiteres Element eingefügt werden soll, in ein neues größeres Array umkopiert werden. Man wählt typischerweise ein doppelt so großes Array.
Beim Einfügen eines Elements inkrementiert man den Arrayindex, beim Löschen dekrementiert man ihn. Man initialisiert ihn mit -1, so dass das erste Element am Index 0 eingefügt wird. Alle Operationen eines Stacks haben eine Laufzeit von
String umkehren
[Bearbeiten]Wir wollen bei einem gegebenen String die Reihenfolge der Buchstaben umkehren. Ein Stack bietet hier eine einfache Lösung. Wir legen geben die Buchstaben in der ursprünglichen Reihenfolge auf den Stack und entnehmen anschließen jeweils das oberste Element des Stacks und fügen es hinten an unseren entstehenden Resultatstring an. Die folgende Abbildung verdeutlicht dieses Vorgehen schematisch. Stacks sind, wie wir hier sehen gut geeignet, um Reihenfolgen umzukehren.
Die Funktion reverse überführt einen String in seine revertierte Version. Wir schreiben den String in einer Schleife zeichenweise auf den Stack. Als Resultat beginnen wir mit dem leeren String. Nun räumen wir den Stack mit einer while not isEmpty(s) Schleife wieder ab. In Körper der Schleife fügen wir das jeweilige oberste Element an unser Resultat an und nehmen anschließend das oberste Element von Stack herunter. Schließlich geben wir das Resultat zurück.
reverse(t : String) : String
s := newStack()
for i := 0 to t.length() -1
push(t.charAt(i), s)
n := ""
while not isEmpty(s)
n := n + top(s)
pop(s)
return n
Klammerung prüfen
[Bearbeiten]Stacks haben auch viel mit symmetrischen Dingen zu tun. Beispielsweise sollte die Klammerung bei einem geklammerten Ausdruck symmetrisch sein. Betrachten wir folgenden Ausdruck aus runden und eckigen Klammern und untersuchen wir ob dieser korrekt geklammert ist.
Die Klammerpaare sind in der obigen Abbildung durch Unterstriche verdeutlicht. Man kann einen Stack auch hier geschickt einsetzen, um die Korrektheit der Klammerung zu überprüfen. Man verarbeitet die Eingabe zeichenweise von links nach rechts. Findet man eine öffnende Klammer, so legt man sie auf den Stack. Findet man eine schließende Klammer in der Eingabe und eine passende öffnende Klammer oben auf dem Stack, so nimmt man sie vom Stack herunter und fährt fort. Findet man eine schließende Klammer und ist der Stack leer oder enthält als Topelement keine passende öffnende Klammer, so hat man gezeigt, dass der Ausdruck falsch geklammert ist. Erreicht man das Ende der Eingabe, so ist der Ausdruck genau dann korrekt geklammert, wenn der Stack nun leer ist.
testeKlammerung(c : Char []) : boolean
s := newStack()
for i := 0 to c.length -1
if c[i] = '(' or c[i] = '['
push(c[i], s)
else
if (
(
( c[i] = ')' and top(s) = '(' )
or ( c[i] = ']' and top(s) = '[' )
)
and
(
not isEmpty(s)
)
)
pop(s)
else
return false
return isEmpy(s)
Infix nach Postfix konvertieren
[Bearbeiten]Wir betrachten folgende Eingabe:
a * (b + c) - d / e
In Postfix Schreibweise lautet der Term entsprechend:
a b c + * d e / -
Auch hier hilft ein Stack diese Umwandlungsaufgabe einfach, zu lösen. Man betrachtet hier einen zunächst leeren Stack sowie eine zeichenweise Eingabe und eine zeichenweise Ausgabe, in welcher wir das Ergebnis erstellen. Wir gehen die Eingabe zeichenweise durch. Finden wir einen Operanden, so schreiben wir ihn in die Ausgabe. Finden wir einen Operator oder eine öffnende Klammer, so legen wir ihn bzw. sie auf den Stack. Bei einer schließenden Klammer lesen und entfernen wir solange Operatoren vom Stack und schreiben, sofern es sich um Operatoren handelt, diese in die Ausgabe, bis wir eine schließende Klammer vom Stack entfernt haben, die Klammer selbst verarbeiten wir nicht weiter.
Weiterhin müssen wir noch berücksichtigen, dass die Multiplikation eine höhere Priorität hat als die Addition (Punkt- vor Strichrechnung). Finden wir einen Operator der Strichrechnung in an der aktuellen Stelle der Eingabe vor, so löschen wir alle Punktrechnungsoperatoren vom Stack und schreiben diese unmittelbar in die Ausgabe. Anschließend legen wir den gefundenen Operator der Strichrechnung auf den Stack.
Queue
[Bearbeiten]Queue
[Bearbeiten]Eine Queue funktioniert genau umgekehrt zu einem Stack. Das Element, welches als Erstes eingefügt wurde, wird auch als Erstes wieder herausgenommen. Das Prinzip ist von der Warteschlange an einer Supermarktkasse her vertraut.
ADT Queue: = ggfs. leere Folge von Elementen zusammen mit einem ggfs. undefinierten Frontelement
Grafisch stellt sich die Situation wie folgt dar:

Bei einer Queue kann man nur am Kopf lesen und nur am Schwanz einfügen. Dieses Verhalten kennt man von Warteschlangen. Elemente innerhalb der Warteschlange werden nicht verschoben.
Eine Queue kennt folgende Operationen
- newQueue() Queue
- isEmpty(q) boolean
- enq(x, q) Queue
- front(q) Element
- deq(q) Queue
Die Operation zum Anfügen heißt enq im Gegensatz zum Stack für sie jedoch am Ende ein. Die deq Operation entfernt das erste Element am Kopf der Schlage. Durch die Operation front wird das Kopfelement der Schlange zurückgeliefert, jedoch nicht entfernt.
Praktische Beispiele für die Verwendung von Queue sind einfache Prozessoren, welche die Befehle aus dem Befehlsspeicher nacheinander abarbeiten. Ein weiteres Beispiel sind Callcenter. Hier ist zu beachten, dass es mehrere Verbraucher gibt, welche Elemente aus der Queue entfernen. Somit sind Synchronisationsstrukturen notwendig. Auch bei Webservern finden Queues Verwendung, da sie ihre Anfragen in der Reihenfolge des Eingangs bearbeiten.
Im folgenden Beispiel betrachten wir eine Liste zur Implementierung einer Queue:

Neben, der Liste mit den Elementen x, y und z benötigen wir sowohl einen Zeiger head auf den Kopf der Liste als auch einen Zeiger tail auf das letzte Element der Liste
deq()
head := head.next
Bäume
[Bearbeiten]Dynamische Datenstrukturen
[Bearbeiten]Auf dieser Seite wird es eine Einführung in die dynamischen Datenstrukturen geben. Unter dynamischen Datenstrukturen verstehen wir Datenstrukturen bei denen man Elemente löschen und hinzufügen kann, eine interne Ordnung (z.B. Sortierung) vorliegt und diese Ordnung unter Änderungen aufrecht erhalten bleibt. Ein Beispiel sind Lineare Datenstrukturen und Sortierung. Bei unsortierte Liste sind Änderung einfach, aber Zugriff aufwändig. Bei einer Neusortierung einer Liste sind Änderung schwierig, aber Zugriff einfach. Bei Trade-of ist eine “intelligente Datenstruktur” gesucht, die Änderungen und Zugriffe einfach, sprich effizient, halten. Viele dynamische Datenstrukturen nutzen Bäume als Repräsentation.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 8.5 zu finden.
Bäume
[Bearbeiten]In diesem Kapitel werden Bäume als kurzen Einschub behandelt behandelt. Ein Baumelement e ist ein Tupel mit v vom Wert e und sind die Nachfolger, bzw. Kinder von e. Ein Baum T ist ein Tupel mit r als Wurzelknoten (ein Baumelement) und als Knoten (Baumelemente) des Baumes mit und für alle
Man spricht von einem geordneten Baum, wenn die Reihenfolge der Kinder eines jeden Elements festgelegt ist (schreibe dann statt
Beispiel
[Bearbeiten]
T' ist kein Baum, da ein gemeinsames Kind haben.
Begriffe
[Bearbeiten]Ein Pfad folgt über Kanten zu verbundenen Knoten, dabei existiert zu jedem Knoten genau ein Pfad von der Wurzel. Ein Baum ist immer zusammenhängend und zyklenfrei.
Das Niveau der jeweiligen Ebene entspricht immer der jeweiligen Länge des Pfades. Die Höhe eines Baumes entspricht dem größten Niveau+1.
Anwendungen
[Bearbeiten]Man benutzt Bäume beispielsweise zur Darstellung von Hierarchien, wie Taxonomien, oder für Entscheidungsbäume. Bäume werden oft genutzt um sortierte, dynamische oder lineare Datenstrukturen zu repräsentieren, da Einfüge-und Löschoperationen leicht so definiert werden können, dass die Sortierung beibehalten wird. Ein Baum kann auch als Datenindex genutzt werden und stellt so eine Alternative zu Listen und Arrays dar.
Hier wird beispielsweise nach der 5 gesucht und der Baum wird als Suchbaum genutzt.
Man kann auch einen Baum aus Termen bilden. Der Term (3+4) * 5 + 2 * 3 gibt folgenden Baum:
Atomare Operationen auf Bäumen
[Bearbeiten]Zu den Operationen zählen lesen mit
- root(): Wurzelknoten eines Baums
- get(e): Wert eines Baumelements e
- children(e): Kinderknoten eines Elements e
- parent(e): Elternknoten eines Elements e
und schreiben mit
- set(e,v): Wert des Elements e auf v setzen
- addChild(e,e’): Füge Element e’ als Kind von e ein (falls geordneter Baum nutze addChild(e,e’,i) für Index i)
- del(e): Lösche Element e (nur wenn e keine Kinder hat)
Spezialfall: Binärer Baum als Datentyp
[Bearbeiten]
class TreeNode<K extends Comparable<K>>{
K key;
TreeNode<K> left = null;
TreeNode<K> right = null;
public TreeNode(K e) {key = e; }
public TreeNode<K> getLeft() {return left; }
public TreeNode<K> getRight() {return right; }
public K getKey() {return key; }
public void setLeft(TreeNode<K> n) {left = n;}
public void setRight(TreeNode<K> n) {right = n;}
...
}
Beispiel
[Bearbeiten]TreeNode<Character> root = new TreeNode<Character>(‘A‘);
TreeNode<Character> node1 = new TreeNode<Character>(‘B‘);
TreeNode<Character> node2 = new TreeNode<Character>(‘C‘);
TreeNode<Character> node3 = new TreeNode<Character>(‘D‘);
root.setLeft(node1);
root.setRight(node2);
node2.setLeft(node3);
Typische Problemstellungen
[Bearbeiten]Als typische Problemstellung haben wir zum einen die Traversierung, zum Anderen das Löschen eines inneren Knotens und die daraus folgende Re-strukturierung des Baumes und das Suchen in Bäumen.
Traversierung
[Bearbeiten]Bäume können visuell gut dargestellt werden. Manchmal ist jedoch eine Serialisierung der Elemente eines Baumes nötig. Man kann die Elemente eines Baumes durch Preorder-Aufzählung, Inorder-Aufzählung, Postorder-Aufzählung oder Levelorder-Aufzählung eindeutig aufzählen.
Bei der Traversierung werden systematisch alle Knoten des Baumes durchlaufen.
Preorder (W-L-R):
Inorder (L-W-R):
Postorder (L-R-W):
Levelorder:
Traversierung mit Iteratoren
[Bearbeiten]Bei der Traversierung sind Iteratoren erlaubt. Diese werden schrittweise abgearbeitet und es werden Standardschleifen für die Baumdurchläufe verwendet.
for (Integer i : tree)
System.out.print(i);
Dabei ist es allerdings notwendig, dass der Bearbeitungszustand zwischengespeichert wird.
public class BinarySearchTree<K extends Comparable<K>>
implement Iterable<K> {
public static final int INORDER = 1;
public static final int PREORDER = 2;
public static final int POSTORDER = 3;
public static final int LEVELORDER = 4;
private int iteratorOrder;
...
public void setIterationOrder(int io) {
if (io < i || io > 4)
return;
iteratorOrder = io;
}
public Iterator<K> iterator() {
switch (iterationOrder) {
case INORDER:
return new InorderIterator<K>(this);
case PRORDER:
return new PreorderIterator<K>(this);
case POSTORDER:
return new PostorderIterator<K>(this);
case LEVELORDER:
return new LevelorderIterator<K>(this);
default:
return new InorderIterator<K>(this);
}
}
Preorder Traversierung
[Bearbeiten]Bei der Preorder Traversierung wird der aktuelle Knoten zuerst behandelt und dann der linke oder rechte Teilbaum.
static class TreeNode<K extends Comparable<K>> {
...
public void traverse() {
if (key==null)
return;
System.out.print(” ” + key);
left.traverse();
right.traverse();
}
Preorder Iteratoren
[Bearbeiten]Der Wurzelknoten wird auf den Stack gelegt, anschließend der rechte Knoten und dann der linke Knoten.
class PreorderIterator<K extends Comparable <K>>
implements Iterator<K> {
java.util.Stack<TreeNode<K>> st =
new java.util.Stack<TreeNode<K>>();
public PreorderIterator(BinarySearchTree<K> tree){
if (tree.head.getRight() != nullNode)
st.push(tree.head.getRight());
}
public boolean hasNext() {
return !st.isEmpty();
}
public K next(){
TreeNode<K> node = st.pop();
K obj = node.getKey();
node = node.getRight();
if(node != nullNode) {
st.push(node); //rechten Knoten auf den Stack
}
node = node.getLeft();
if(node != nullNode) {
st.push(node); //linken Knoten auf den Stack
}
return obj;
}
}
Inorder Traversierung
[Bearbeiten]Bei der Inorder Traversierung wird zuerst der linke Teilbaum behandelt, dann der aktuelle Knoten und dann der rechte Teilbaum. Als Ergebnis erhält man den Baum in sortierter Reihenfolge.
static class TreeNode<K extends Comparable<K>> {
...
public void traverse() {
if (key==null)
return;
left.traverse();
System.out.print(” ” + key);
right.traverse();
}
Inorder Iteratoren
[Bearbeiten]Der Knoten head hat immer einen rechten Nachfolger. Es wird vom Wurzelknoten begonnen alle linken Knoten auf den Stack zu legen.
class InorderIterator<K extends Comparable <K>>
implements Iterator<K> {
java.util.Stack<TreeNode<K>> st =
new java.util.Stack<TreeNode<K>>();
public InorderIterator(BinarySearchTree<K> tree) {
TreeNode<K> node = tree.head.getRight();
while (node != nullNode) {
st.push(node);
node = node.getLeft();
}
}
public boolean hasNext() {
return !st.isEmpty();
}
public K next(){
TreeNode<K> node = st.pop();
K obj = node.getKey();
node = node.getRight(); //rechten Knoten holen
while (node != nullNode) {
st.push(node);
node = node.getLeft(); //linken Knoten auf den Stack
}
return obj;
}
}
Postorder Traversierung
[Bearbeiten]Bei der Postorder Traversierung wird zuerst der linke und der rechte Teilbaum behandelt und dann der aktuelle Knoten. Dies kann beispielsweise genutzt werden, um einen Baum aus Termen, entsprechend der Priorität der Operatoren, auszuwerten.
static class TreeNode<K extends Comparable<K>> {
...
public void traverse() {
if (key==null)
return;
left.traverse();
right.traverse();
System.out.print(” ” + key);
}
Levelorder Iteratoren
[Bearbeiten]Der Wurzelknoten wird in der Warteschlange eingefügt. Dann wird zuerst der linke und dann der rechte Knoten in die Warteschlange eingefügt. In dieser Implementierung wird die queue als LinkedList repräsentiert. Dies ist jedoch beliebig.
class LevelorderIterator<K extends Comparable <K>>
implements Iterator<K> {
//Wurzelknoten in die Warteschlange (queue) einfügen
java.util.Queue<TreeNode<K>> q =
new java.util.LinkedList<TreeNode<K>>();
public LevelorderIterator(BinarySearchTree<K> tree){
TreeNode<K> node = tree.head.getRight();
if (node != nullNode)
q.addLast(node);}
public K next(){
TreeNode<K> node = q.getFirst();
K obj = node.getKey();
if (node.getLeft() != nullNode)
q.addLast(node.getLeft());
if (node.getRight() != nullNode)
q.addLast(node.getRight());
return obj;
}
}
Bäume in Java
[Bearbeiten]In Java gibt es keine hauseigene Implementierung für allgemeine Bäume. Einige Klassen (TreeMap, TreeSet) benutzen Bäume zur Realisierung anderer Datenstrukturen. Andere Klassen (JTree) benutzen Bäume als Datenmodell zur Visualisierung.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14 zu finden.
Binäre Bäume
[Bearbeiten]Suchbäume
[Bearbeiten]Einleitung Binäre Suchbäume
[Bearbeiten]Auf dieser Seite werden die binären Suchbäume behandelt. Er ermöglicht einen schneller Zugriff auf Daten mit dem Aufwand O(log n) unter geeigneten Voraussetzungen. Des weiteren ermöglicht er effiziente Sortierung von Daten, durch Heapsort und effiziente Warteschlangen. Der binäre Suchbaum dient als Datenstruktur für kontextfreie Sprachen. In der Computergrafik sind Szenengraphen oft (Beinahe-)Bäume. Bei Informationssysteme dienen binäre Suchbäume zur Datenindizierung und Anfrageoptimierung.
Operationen
[Bearbeiten]Auf Suchbäumen können die Operationen Suchen von Elementen, Einfügen von Elementen und Entfernen von Elementen angewandt werden, wobei letztere zwei voraussetzen, dass die Ordnung der Schlüssel erhalten bleibt.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14 zu finden.
Suchen
[Bearbeiten]Ein binärer Suchbaum kann für viele Anwendungen eingesetzt werden.
Hier ist der Baum ein Datenindex und eine Alternative zu Listen und Arrays. Beispielsweise kann dieser Baum als Suchbaum verwendet werden und nach "5" gesucht werden.
Bei der Anwendung von Bäumen zur effizienten Suche gibt es pro Knoten einen Schlüssel und ein Datenelement und die Ordnung der Knoten erfolgt anhand der Schlüssel. Bei einem binärer Suchbaum enthält der Knoten k einen Schlüsselwert k.key. Alle Schlüsselwerte im linken Teilbaum k.left sind kleiner als k.key und alle Schlüsselwerte im rechten Teilbaum k.right sind größer als k.key. Die Auswertung eines Suchbaums sieht wie folgt aus:
- Vergleich des Suchschlüssels mit Schlüssel der Wurzel
- Wenn kleiner, dann in linken Teilbaum weiter suchen
- Wenn größer, dann in rechtem Teilbaum weiter suchen
- Sonst gefunden/nicht gefunden
static class TreeNode<K extends Comparable<K>>{
K key;
TreeNode<K> left = null;
TreeNode<K> right = null;
public TreeNode(K e) {key = e; }
public TreeNode<K> getLeft() {return left; }
public TreeNode<K> getRight() {return right; }
public K getKey() {return key; }
public void setLeft(TreeNode<K> n) {left = n;}
public void setRight(TreeNode<K> n) {right = n;}
...
}
Knotenvergleich
[Bearbeiten]class TreeNode<...> {
...
public int compareKeyTo(K k) {
return (key == null ? -1:
key.compareTo(k));
}
...
}
Rekursives Suchen
[Bearbeiten]protected TreeNode<K>
recursiveFindNode(TreeNode<K> n, k){
/* k wird gesucht */
if (n!= nullNode) {
int cmp = n.compareKeyTo(k.key);
if (cmp == 0)
return n;
else if (cmp > 0)
return
recursiveFindNode(n.getLeft(),k);
else
return
recursiveFindNode(n.getRight(),k);
}
else
return null;
}
Iteratives Suchen
[Bearbeiten]protected TreeNode<K> iterativeFindNode(TreeNode<K> k){
/* k wird gesucht */
TreeNode<K> n = head.getRight();
while (n!= nullNode) {
int cmp = n.compareKeyTo(k.key);
if (cmp == 0)
return n;
else
n = (cmp > 0 ?
n.getLeft(): n.getRight());
}
return null;
}
Suchen des kleinsten Elements
[Bearbeiten]protected K findMinElement(){
TreeNode<K> n = head.getRight();
while (n.getLeft() != nullNode)
n = n.getLeft();
return n.getKey();
}
Suchen des größten Elements
[Bearbeiten]protected K findMaxElement(){
TreeNode<K> n = head.getRight();
while (n.getRight() != nullNode)
n = n.getRight();
return n.getKey();
}
Eine weitere Anwendungsmöglichkeit ist der Baum aus Termen. Wir haben den Term als Baumdarstellung sieht es so aus:
Bei der Auswertung müssen die Operatoren auf die beiden Werte der Teilbäume angewandt werden.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.3 zu finden.
Einfügen
[Bearbeiten]Das Finden der Einfügeposition erfolgt durch Suchen des Knotens, dessen Schlüsselwert größer als der einzufügende Schlüssel ist und der keinen linken Nachfolger hat oder durch Suchen des Knotens, dessen Schlüsselwert kleiner als der einzufügende Schlüssel ist und der keinen rechten Nachfolger hat. Das Einfügen erfolgt prinzipiell in 2 Schritten. Im ersten Schritt wird die Einfügeposition gesucht, sprich der Blattknoten mit dem nächstkleineren oder nächstgrößerem Schlüssel. Im zweiten Schritt wird ein neuer Knoten erzeugt und als Kindknoten des Knotens aus Schritt eins verlinkt. Wenn in Schritt eins der Schlüssel bereits existiert, dann wird nicht erneut eingefügt.
Programm in Java
[Bearbeiten] /* Einfügeposition suchen */
public boolean insert(K k){
TreeNode<K> parent = head;
TreeNode<K> child = head.getRight();
while (child != nullNode) {
parent = child;
int cmp = child.compareKeyTo(k);
//Schlüssel bereits vorhanden
if (cmp == 0)
return false;
else if (cmp > 0)
child = child.getLeft();
else
child = child.getRight();
}
/* Neuen Knoten verlinken */
TreeNode<K> node = new TreeNode<K>(k);
node.setLeft(nullNode);
node.setRight(nullNode);
if (parent.compareKeyTo(k) > 0)
parent.setLeft(node);
else
parent.setRight(node);
return true;
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.3.2 zu finden.
Löschen
[Bearbeiten]Zuerst wird das zu löschendes Element gesucht, der Knoten k. Nun gibt es drei Fälle
- k ist Blatt: löschen
- k hat ein Kind: Kind „hochziehen“
- k hat zwei Kinder: Tausche mit weitest links stehenden Kind des rechten Teilbaums, da dieser in der Sortierreihenfolge der nächste Knoten ist und entferne diesen nach den Regeln 1. oder 2.
Ein Schlüssel wird in drei Schritten gelöscht. Im ersten Schritt wird der zu löschende Knoten gefunden. Im zweiten Schritt wird der Nachrückknoten gefunden. Dafür gibt es mehrere Fälle. Im Fall 1 handelt es sich um einen externen Knoten, sprich ein Blatt, ohne Kinder. Dabei wird der Knoten durch einen nullNode ersetzt. Im Fall 2a gibt es nur einen rechten Kindknoten, dabei wird der gelöschte Knoten durch den rechten Kindknoten ersetzt. Im Fall 2b gibt es nur einen linken Kindknoten und der gelöschte Knoten wird durch diesen ersetzt. Im Fall 3 gibt es einen internen Knoten mit Kindern rechts und links. Dabei wird der gelöschte Knoten durch den Knoten mit dem kleinstem (alternativ größtem) Schlüssel im rechten (alternativ linken) Teilbaum ersetzt. im dritten und letzten Schritt wird nun der Baum reorganisiert. Während dem Löschen kann sich die Höhe von Teilbäumen ändern.
Programm in Java
[Bearbeiten] /* Knoten suchen */
public boolean remove(K k){
TreeNode<K> parent = head;
TreeNode<K> node = head.getRight();
TreeNode<K> child = null;
TreeNode<K> tmp = null;
while (node != nullNode) {
int cmp = node.compareKeyTo(k);
//Löschposition gefunden
if (cmp == 0)
break;
else {
parent = node;
node = (cmp > 0 ?
node.getLeft() : node.getRight());
}
}
//Knoten k nicht im Baum
if (node == nullNode)
return false;
/* Nachrücker finden */
if (node.getLeft() == nullNode &&
Node.getRight() == nullNode) //Fall 1
child = nullNode;
else if (node.getLeft() == nullNode) //Fall 2a
child = node.getRight();
else if (node.getRight() == nullNode) //Fall 2b
child = node.getLight();
...
//Fall 3
else {
child = node.getRight();
tmp = node;
while (child.getLeft() != nullNode) {
tmp = child;
child = child.getLeft();
}
child.setLeft(node.getLeft());
if (tmp != node) {
tmp.setLeft(child.getRight());
child.setRight(node.getRight());
}
}
/* Baum reorganisieren */
if (parent.getLeft() == node)
parent.setLeft(child)
else
parent.setRight(child);
return true;
...
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.3.2 zu finden.
Implementierung
[Bearbeiten]Ein binärer Suchbaum ist eine häufig verwendete Hauptspeicherstruktur und ist besonders geeignet für Schlüssel fester Größe, z.B. numerische wie int, float und char[n]. Der Aufwand von O(log n) für Suchen, Einfügen und Löschen ist garantiert, vorausgesetzt der Baum ist balanciert. Später werden wir lernen, dass die Gewährleistung der Balancierung durch spezielle Algorithmen gesichert wird. Des weiteren sind größere, angepasste Knoten für Sekundärspeicher günstiger, diese nennt man B-Bäume. Für Zeichenketten benutzt man als Schlüssel variable Schlüsselgröße, sogenannte Tries.
public class
BinarySearchTree<K extends Comparable<K>>
implements Iterable<K> {
...
static class TreeNode<K extends Comparable<K>> {
K key;
TreeNode<K> left = null;
TreeNode<K> right = null;
...
}
}
Die Schlüssel müssen Comparable-Interface, d.h. compareTo()-Methode, implementieren, da der Suchbaum auf Vergleichen der Schlüssel basiert. Der Baum selbst implementiert Iterable-Interface, d.h. iterator()-Methode, um Traversierung des Baums über Iterator zu erlauben (später Baumtraversierung).TreeNode und alles weitere werden als innere Klassen implementiert. Dadurch werden Zugriff auf Attribute und Methoden der Baumklasse erlaubt. Eine Besonderheit der Implementierung sind die „leeren“ Pseudoknoten head und nullNode zur Vereinfachung der Algorithmen (manchmal „Wächter“ / „sentinel“ genannt). Grundlegende Algorithmen sind
- Suchen
- Einfügen
- Löschen
Implementierung mit Pseudoknoten
[Bearbeiten]Wir vereinbaren an dieser Stelle, dass man auf dem Kopf kein getRight() anwenden kann.
public class
BinarySearchTree<K extends Comparable<K>>
implements Iterable<K> {
...
pulic BinarySearchTree(){
head = new TreeNode<K>(null);
nullNode = new TreeNode<K>(null);
nullNode.setLeft(nullNode);
nullNode.setRight(nullNode);
head.setRight(nullNode);
}
...
}
Das Ziel der Implementierung ist, die Reduzierung der Zahl an Sonderfällen. Im head würde das Einfügen oder Löschen des Wurzelknotens spezielle Behandlung in der Baum-Klasse erfordern. Der nullNode erspart den Test, ob zum linken oder zum rechten Teilknoten navigiert werden kann. Des weiteren ist im NullNode ein einfaches Beenden der Navigation (z.B. Beenden der Rekursion) möglich.
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.2.1 zu finden.
Weitere Aspekte
[Bearbeiten]Die Komplexität der Operation hängt von der Höhe ab. Der Aufwand für die Höhe des Baumes beträgt O(h). Die Höhe eines ausgeglichenen binären Baumes ist h=ld(n) für Knoten. Bei eines ausgeglichenen oder balancierten Baum unterscheiden sich zum einen der rechte und linke Teilbaum eines jeden Knotens in der Höhe um höchstens 1 und zum anderen unterscheiden sich je zwei Wege von der Wurzel zu einem Blattknoten höchstens in um 1 in der Länge. Rot-Schwarz Bäume und AVL Bäume benötigen einen Ausgleich nach dem Einfügen und Löschen.
Entartung von Bäumen
[Bearbeiten]Ungünstige Einfüge- oder Löschreihenfolge führt zu extremer Unbalanciertheit. Im Extremfall wird der Baum zur Liste, dann haben die Operationen eine Komplexität von O(n). Beispiel:
for (int i = 0; i < 10; i++) tree.insert(i);
Vermeiden kann man dies durch spezielle Algorithmen zum Einfügen und Löschen, z.B. mit Rot-Schwarz-Bäumen und AVL-Bäumen.
AVL Bäume
[Bearbeiten]Auf dieser Seite werden AVL Bäume behandelt. Ein Suchbaum erfordert nach Einfügen oder Löschen von Knoten einen Ausgleich, da sie sonst entarten. AVL steht für die russischen Mathematiker Adelson-Velskii und Landis. Liegt ein binärer Suchbaum mit AVL Kriterium vor, bedeutet das, dass für jeden inneren Knoten gilt: Die Höhe des linken und rechten Teilbaums differieren maximal um 1. Es reicht nicht diese Bedingung nur für die Wurzel zu fordern, da beide Teilbäume der Wurzel entartet sein könnten.
Als Lösungsidee gibt es zwei Ansätze. Zum einen ein abgeschwächtes Kriterium für die ausgeglichene Höhe, beispielsweise AVL Bäume und zum anderen eine ausgeglichene Höhe, aber ein unausgeglichener Verzweigungsgrad. Dabei können wir eine direkte Realisierung als Mehrwegbäume, beispielsweise B-Bäume, nutzen, oder eine Kodierung als binären Baum, beispielsweise Rot-Schwarz-Bäume.
AVL Eigenschaften
[Bearbeiten]Höhe von AVL Bäumen
[Bearbeiten]Wie viele Knoten hat ein AVl Baum der Höhe h mindestens? Bei einer rekursiven Beziehung ist , d.h der Baum hat nur eine Wurzel. Bei , das heißt der Baum hat nur einen Zweig und bei , das heißt der Baum hat mehr Zweige. Daraus lässt sich allgemein sagen, dass . Damit wächst der Baum vergleichbar mit der Fibonacci Reihe.
Einfügen in AVL Baum
[Bearbeiten]Das Einfügen eines Schlüssels erfolgt mit den üblichen Algorithmen. Es kann aber passieren, dass danach die AVL Eigenschaft verletzt ist. Die Balance ist definiert als left.height-right.height. Als AVL Eigenschaft muss die Balance sein. Nach Einfügen ist die Balance aber Reparieren kann man das Ganze mittels Rotation und Doppelrotation.
Fallunterscheidung
[Bearbeiten]Beim Einfügen kann man in verschiedene Fälle unterteilen. Eine Verletzung der AVL Eigenschaft tritt ein bei
- Einfügen in linken Teilbaum des linken Kindes
- Einfügen in rechten Teilbaum des linken Kindes
- Einfügen in linken Teilbaum des rechten Kindes
- Einfügen in rechten Teilbaum des rechten Kindes
1 und 4 sowie 2 und 3 sind symmetrische Problemfälle.
Einfache Rotation
[Bearbeiten]Wir haben eine Rotation mit linkem Kind nach rechts oder rechtem Kind nach links.
Doppelrotation
[Bearbeiten]Wir haben eine Doppelrotation mit linkem Kind nach rechts oder rechtem Kind nach links.
Beispiel
[Bearbeiten]Im Folgenden werden wir die Rotation an einem Beispiel veranschaulichen.
insert 3, 2, 1
→ einfache Rotation nach rechts (2,3)
insert 4, 5
→ einfache Rotation nach links (4,3)
insert 6
→ einfache Rotation (Wurzel) nach links (4,2)
insert 7
→ einfache Rotation nach links (6,5)
insert 16, 15
→ Doppelrotation nach links (7,15,15)
insert 13+12+11+10
→ jeweils einfache Rotation
insert 8, 9
→ Doppelrotation nach rechts
Eine Verletzung der AVL-Eigenschaft tritt ein
- Beim Einfügen in linken Teilbaum des linken Kindes, dann muss eine Rotation mit dem linkem Kind erfolgen
- Beim Einfügen in rechten Teilbaum des linken Kindes, dann muss eine Doppelrotation mit dem linken Kind erfolgen
- Beim Einfügen in linken Teilbaum des rechten Kindes, dann muss eine Doppelrotation mit dem rechten Kind erfolgen
- Beim Einfügen in rechten Teilbaum des rechten Kindes, dann muss eine Rotation mit dem rechten Kind erfolgen
Implementation
[Bearbeiten]Die Implementierung ist ähnlich des binären Suchbaums. Der Aufruf um einen neuen Knoten hinzuzufügen geschieht dabei mit AvlTree.insert(K k).
public class AvlTree<K extends Comparable<K>> {
private AvlTreeNode<K> head;
private AvlTreeNode<K> nullNode; //Neuer Knotentyp
public AvlTree(){
head = new AvlTreeNode<K>(null);
nullNode = new AvlTreeNode<K>(null);
nullNode.setLeft(nullNode);
nullNode.setRight(nullNode);
head.setRight(nullNode);
}
public boolean insert(K k){
AvlTreeNode<K> parent = head;
AvlTreeNode<K> child = head.getRight();
while(child != nullNode){
parent = child;
int cmp = child.getKey().compareTo(k);
if(cmp == 0)
return false;
else if (cmp > 0)
child = child.getLeft();
else
child = child.getRight();
}
AvlTreeNode<K> node = new AvlTreeNode<K>(k);
node.setLeft(nullNode);
node.setRight(nullNode);
node.setParent(parent);
if(parent.compareTo(node) > 0)
parent.setLeft(node);
else
parent.setRight(node);
//Nach der Einfügung die Balance ggfs. reparieren
parent.repair(node, nullNode);
return true;
}
}
Die Knotenimplementierung ist zu Beginn genauso wie beim binären Suchbaum. Die Methoden balance() und height() dienen als Hilfe für die Balance. Weiterhin wird die Methode repair() zur Reparatur der Balance benötigt. Sie testet, ob die Balance für den aktuellen Knoten (this) verletzt ist und repariert diese gegebenenfalls.
class AvlTreeNode<K extends Comparable<K>>{
K key;
private AvlTreeNode<K> left;
private AvlTreeNode<K> right;
private AvlTreeNode<K> parent; //für jeden Knoten merken wir uns nun den Elternknoten
public AvlTreeNode(K key){
this.left = null;
this.right = null;
this.parents = null;
this.key = key;
}
public AvlTreeNode<K> getLeft() { return left; }
public AvlTreeNode<K> getRight() { return right; }
public K getKey() { return key; }
public void setLeft(AvlTreeNode<K> n) { left = n; }
public void setRight(AvlTreeNode<K> n) { right = n; }
public void setParent(AvlTreeNode<K> n) { parent = n; }
public int compareTo(AvlTreeNode<K> other){
return (this.key == null) ? -1 : this.key.compareTo(other.key);
}
//Positive Balance, falls linker Teilbaum größer als der rechte Teilbaum
//Negative Balance, falls rechter Teilbaum größer als der linke Teilbaum
//Balance = 0, falls ausgeglichen
public int balance(){
if(this.key == null) //Nullknoten sind stets ausgeglichen
return 0;
return this.left.height() - this.right.height();
}
//Gibt die Länge des längsten Pfades zu einem Blatt wieder
public int height(){
if(this.key == null) //Nullknoten haben die Höhe 0
return 0;
return Math.max(this.left.height(), this.right.height()) + 1;
}
//Es werden die zwei nachfolgenden Knoten auf dem Pfad der Einfügung übergeben
//man startet vom Punkt der Einfügung, einem Blatt und arbeitet sich von unten nach oben
public void repair(AvlTreeNode<K> child, AvlTreeNode<K> grandchild){
//Falls wie am head angekommen sind, terminieren wir
if(this.key == null)
return;
//Fall 1: Einfügen im linken Teilbaum des linken Kindes
if(this.balance() > 1 && child.balance() > 0){
child.parent = this.parent;
this.parent = child;
this.left = child.right;
child.right = this;
if(child.parent.left == this)
child.parent.left = child;
else child.parent.right = child;
}
//Fall 2: Einfügung im rechten Teilbaum des linken Kindes
if(this.balance() > 1 && child.balance() < 0){
grandchild.parent = this.parent;
this.parent = grandchild;
this.left = grandchild.right;
this.left.parent = this;
grandchild.right = this;
child.right = grandchild.left;
child.right.parent = child;
grandchild.left = child;
child.parent = grandchild;
if(grandchild.parent.left == this)
grandchild.parent.left = grandchild;
else grandchild.parent.right = grandchild;
}
//Fall 3 und 4 wären analog
//Fahre rekursiv mit Elternknoten fort
this.parent.repair(this, child);
}
}
Literatur
[Bearbeiten]Da die Vorlesungsinhalte auf dem Buch Algorithmen und Datenstrukturen: Eine Einführung mit Java von Gunter Saake und Kai-Uwe Sattler aufbauen, empfiehlt sich dieses Buch um das hier vorgestellte Wissen zu vertiefen. Die auf dieser Seite behandelten Inhalte sind in Kapitel 14.4.2 zu finden.
Quad Tree
[Bearbeiten]Hashing
[Bearbeiten]Hashtabellen
[Bearbeiten]Auf dieser Seite wird das Thema Hashtabellen behandelt. Gesucht ist eine dynamische Datenstruktur mit sehr schnellem direktem Zugriff auf Elemente. Die Idee der Hashfunktion ist, dass ein Feld von 0 bis N-1 benutzt wird, beispielsweise ein Array. Die einzelnen Positionen im Feld werden oft als Buckets bezeichnet. Die Hashfunktion h(e) bestimmt für Elemente e die Position im Feld. H(e) ist sehr schnell berechenbar. Es gilt
Beispiele
[Bearbeiten]Wir haben ein Array von 0 bis 9 und h(i)=i mod 10. Das Array sieht nach dem Einfügen der Zahlen 42 und 119 wie folgt aus:
| Index | Eintrag |
| 0 | |
| 1 | |
| 2 | 42 |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | 119 |
Der Vorteil von Hashing ist, dass Anfragen der Form " Enthält die Datenstruktur das Element 42?" schnell beantwortbar sind. Dazu verhalten sich Hashtabellen ähnlich zu binären Suchbäumen wie BucketSort zu vergleichsbasierten Sortierverfahren.
Hashfunktionen
[Bearbeiten]Die Hashfunktionen hängen vom Datentyp der Elemente und der konkreten Anwendungen ab. Für den Datentyp Integer ist die Hashfunktion meist h(i)=i mod N. Das funktioniert im Allgemeinen sehr gut, wenn N eine Primzahl ist und hängt mit Methoden zur Erzeugung von Zufallszahlen zusammen. Für andere Datentypen führt man eine Rückführung auf Integer aus. Bei Fließpunkt-Zahlen werden Mantisse und Exponent einfach addiert.
Die Hashwerte sollten gut streuen. Das ist eventuell von den Besonderheiten der Eingabewerte abhängig. Beispielsweise tauchen Buchstaben des Alphabets in Namen unterschiedlich oft auf.
Des weiteren müssen die Hash-Werte effizient berechenbar sein. Ein konstanter Zeitbedarf ist erfordert, dieser ist nicht von der Anzahl der gespeicherten Werte abhängig.
Ungünstige Hashfunktionen
[Bearbeiten]Als erstes Beispiel wählen wir und eine generierte Artikelnummer mit den Kontrollziffern 1,3 oder 7 am Ende. Damit wäre die Abbildung nur auf ungeraden Adressen möglich. Als zweites Beispiel wählen wir Matrikelnummern in einer Hashtabelle mit 100 Einträgen. In der ersten Variante nutzen wir die ersten beiden Stellen als Hashwert, damit kann eine Abbildung nur auf wenige Buckets erfolgen. In der zweiten Variante nutzen wir die beiden letzten Stellen und erhalten eine gleichmäßige Verteilung.
Graphen
[Bearbeiten]Typen von Graphen und Anwendungen
[Bearbeiten]In diesem Kapitel werden Graphen behandelt. Ein Graph ist das mathematische Modell eines Netzwerks bestehend aus Knoten und Kanten. Graphen haben einen vielfältigen Einsatz. So kommen sie bei Verbindungsnetzwerken (Bahnnetz, Flugververbindungen, Straßenkarten, ...), Verweisen (WWW, Literaturverweise, Wikipedia, symbolische Links, ...), Technischen Modellen (Platinen-layout, finite Elemente, Computergrafik) und Software Reengineering und - dokumentation zum Einsatz. Bäume und Listen sind spezielle Graphen.
Ungerichteter Graph
[Bearbeiten]Es gibt verschiedene Typen von Graphen. Der ungerichtete Graph ist beispielsweise eine Straßenverbindung, eine Telefonnetz oder ein soziales Netzwerk. Ein ungerichteter Graph ist ein Tupel G=(V,E). Wir haben eine endliche Menge V von Knoten (Vertices) und eine Menge E von Kanten (Edges), die aus ungeordneten Paaren aus V besteht. Es gilt, dass und jedes ist eine zweielementige Teilmenge der Knotenmenge . Im ungerichteten Graphen gibt es keine Schleifen, das heißt es gibt keine Kanten die von einem Knoten zu sich selbst laufen. Außerdem gibt es keine mehrfachen Kanten zwischen zwei Knoten, Parallelkanten genannt.
Hier können zum Beispiel die kürzesten Wege bei sozialen Netzwerken wie Facebook berechnet werden.
Spezielle Graphen
[Bearbeiten]Sei ein Graph.
G heißt planar, falls er ohne Überschneidungen der Kanten in der Ebene gezeichnet werden kann.
G heißt vollständig, falls
G heißt regulär, falls alle Knoten denselben Grad haben
G heißt bipartit, falls und
- keine zwei Knoten in sind adjazent
- keine zwei Knoten in sind adjazent
Beispiele
[Bearbeiten]Dieser Graph ist sowohl planar, regulär als auch vollständig.

Dieser Graph ist jedoch nur regulär und vollständig.

Hier handelt es sich nur um einen regulären Graphen.

Dies ist ein Beispiel für einen bipartiten Graph.

Gerichteter Graph
[Bearbeiten]Der gerichtete Graph ist beispielsweise eine Förderanlage oder ein Kontrollfluss in Programmen. Der gerichtete Graph (auch Digraph) ist ein Tupel G=(V,E) mit V als endliche Menge von Knoten und E einer Menge von Kanten, geordneten Paaren aus V. Jedes ist nun ein Tupel e=(a,b) mit . Schleifen der Form (a,a) sind nun erlaubt. Dazu ist (a,b) eine andere Kante als (b,a). Der Unterschied zwischen (a,b) und {a,b} besteht darin, dass das Tupel (a,b) geordnet ist. Die Reihenfolge kann nicht verändert werden. Hingegen ist {a,b} eine Menge, in der die Reihenfolge der Elemente keine Rolle spielt.
Gerichtete Graphen werden zum Beispiel als Web-Graph (Google`s PageRank) benutzt. Aber auch in der Scientometrie kommen sie zum Einsatz bei der Impact Faktoren Berechnung. Bei Datenstrukturen im Semantik Web werden gerichtete Graphen zum Speichern von Daten genutzt.
Gerichtete und ungerichtete Graphen
[Bearbeiten]Ein ungerichteter Graph kann in einen gerichteten Graphen transformiert werden, indem jede ungerichtete Kante {v,w} durch zwei gerichtete Kanten (v,w) und (w,v) ersetzt wird. Dann ist beispielsweise der Zusammenhang identisch mit dem starken Zusaamenhang. Dazu haben gerichtete Graphen haben eine größere Ausdrucksstärke und daher wird "Graph" oft als Synonym für einen Digraph verwendet.
Gewichteter Graph
[Bearbeiten]Ein ungerichteter gewichteter Graph ist beispielsweise eine Flugverbindung mit Meilen oder Kosten, ein Straßennetz mit Kilometern oder ein Rohrsystem mit Durchfluss.
Ein gerichteter gewichteter Graph ist beispielsweise eine Straßennetz mit Einbahnstraßen, Rohre mit Ventilen oder ein Förderband.
Der Graph ist ein Paar G=(V,E) und wir haben eine Kantengewichtsfunktion g. Daraus erhalten wir G=(V,E,g) mit . Der Graph kann gerichtet oder ungerichtet sein und die Kantengewichte müssen nicht notwendigerweise natürliche Zahlen sein.
Ungerichtete gewichtete Graphen kommen zum Beispiel bei der Navigation beim Berechnen des kürzesten Weges zum Einsatz.
Gerichtete gewichtete Graphen kommen bei der Optimierung in der Telekommunikation zum Einsatz.
Hypergraph
[Bearbeiten]Es gibt aber noch viele weitere Varianten von Graphen wie Multigraphen oder Hypergraphen.
Ein Hypergraph ist ein Paar G=(V,E) mit einer Menge von Knoten V und einer Menge von Hyperkanten .
Definitionen
[Bearbeiten]Hier werden allgemeine Definitionen bezüglich der Graphen behandelt. Dazu werden immer wieder Beispiele gebracht, die sich auf folgende Graphen beziehen. Dabei gilt je nach Beispiel G=(V,E) entweder für den ungerichteten oder den gerichteten Graphen.
Adjazenz
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Zwei Knoten heißen adjazent, falls .
Hier heißt v heißt auch Nachbar von w.
Beispiel:
- Knoten 1 und 3 sind adjazent
Gerichteter Graph
[Bearbeiten]Zwei Knoten heißen adjazent, falls oder .
Für heißt w Nachfolger von v und v Vorgänger von w.
Beispiele:
- Knoten 1 ist Vorgänger zu Knoten 3
- Knoten 4 ist Nachfolger zu Knoten 6
Inzidenz
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Eine Kante ist inzident zu einem Knoten , falls oder .
Gerichteter Graph
[Bearbeiten]Eine Kante ist inzident zu einem Knoten , falls oder .
Grad
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Der Grad (engl. degree) eines Knotens ist die Anzahl seiner inzidenten Kanten, das heißt: .
Beispiel:
- Der Grad von Knoten 4 ist 3
Gerichteter Graph
[Bearbeiten]Der Eingangsgrad (engl. in-degree) eines Knotens ist die Anzahl seiner Vorgänger: .
Der Ausgangsgrad (engl. out-degree) eines Knotens ist die Anzahl seiner Nachfolger: .
Beispiele:
- Der Eingangsgrad von Knoten 3 ist 2
- Der Ausgangsgrad von Knoten 3 ist 3
Weg
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Ein Weg W ist eine Sequenz von Knoten mit für die gilt:
Beispiel:
- (1,3,5,6,3,4) ist ein Weg
Gerichteter Graph
[Bearbeiten]Ein (gerichteter) Weg W ist eine Sequenz von Knoten .
Beispiel:
- (1,3,6,5,5,3,1) ist ein (gerichteter) Weg
Pfad
[Bearbeiten]Ein Weg W heißt Pfad, falls zusätzlich gilt . Das heißt, der Weg enthält keine doppelten Knoten. Diese Definition gilt sowohl für ungerichtete als auch gerichtete Graphen.
Beispiel:
- (1,4,6,5) ist ein Pfad
Kreis
[Bearbeiten]Ein Weg P heißt Kreis, falls . Dazu ist ein Kreis K elementar, falls . Der Kreis enthält also keine doppelten Knoten bis auf den Anfangs- und den Endpunkt. Diese Definition gilt sowohl für ungerichtete als auch gerichtete Graphen.
Beispiel:
- (1,3,4,6,3,4,1) ist ein Kreis
- (3,4,6,3) ist ein elementarer Kreis
Länge
[Bearbeiten]Die Länge eines Weges ist die Anzahl der durchlaufenen Kanten. Die Länge eines Pfades ist also n-1. Diese Definition gilt sowohl für ungerichtete als auch gerichtete Graphen.
Beispiel:
- Die Länge von (3,4,6,3,4,1) ist 4
- Die Länge von (1,3,6) ist 2
Teilgraph
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Ein Graph heißt Teilgraph von G, falls .
Beispiel:
- G'=({3,4,6},{{3,4},{4,6}}) ist ein Teilgraph von G
Gerichteter Graph
[Bearbeiten]Ein Graph heißt Teilgraph von G, falls und .
Beispiel:
- ist ein Teilgraph von .
Erreichbarkeit
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]Ein Knoten heißt erreichbar von einem Knoten , falls ein Weg existiert mit und .
Beispiele:
- Knoten 6 ist erreichbar von Knoten 1
- Knoten 7 ist nicht erreichbar von Knoten 1
Gerichteter Graph
[Bearbeiten]Ein Knoten heißt erreichbar von einem Knoten , falls ein Weg existiert mit und .
Beispiele:
- Knoten 6 ist erreichbar von Knoten 1
- Knoten 5 ist nicht erreichbar von Knoten 2
Zusammenhang
[Bearbeiten]Ungerichteter Graph
[Bearbeiten]G heißt (einfach) zusammenhängend, falls für alle gilt, dass w von v erreichbar ist
Ein Teilgraph von G heißt Zusammenhangskomponente von G, falls G' zusammenhängend ist und kein Teilgraph von G existert mit .
Beispiele:
- G ist nicht zusammenhängend
- Der Teilgraph ist eine Zusammenhangskomponente von G
- Der Teilgraph ist eine Zusammenhangskomponente von G
Gerichteter Graph
[Bearbeiten]G heißt (stark) zusammenhängend, falls für alle gilt, dass w von v und v von w erreichbar ist.
Ein Teilgraph von G heißt starke Zusammenhangskomponente von G, falls stark zusammenhängend ist und kein Teilgraph von G existiert mit .
Beispiel:
- Der Teilgraph mit und ist eine starke Zusammenhangskomponente von .
Repräsentation von Graphen
[Bearbeiten]Auf dieser Seite wird die Repräsentation von Graphen behandelt. Wir fragen uns wie effizient die Datenstruktur für Graphen ist.
Kanten- und Knotenlisten
[Bearbeiten]Bei durchnummerierten Knoten erfolgt eine einfache Realisierung. Historisch gesehen ist es die erste verwendete Datenstruktur. Außerdem ist sie als Austauschformat geeignet und die Auflistung ist nach Knoten oder nach Kanten sortiert.
Beispiel Kantenliste
[Bearbeiten]
Gegeben ist eine Kantenliste für
Die erste Zahl (6) steht für die Knotenzahl. Die zweite Zahl (11) steht für die Kantenzahl. Die weiteren Paare (1,2 ; 1,3...) stehen für die Kanten.
6,11,1,2,1,3,3,1,4,1,3,4,3,6,5,3,5,5,6,5,6,2,6,4
Beispiel Knotenliste
[Bearbeiten]
Gegeben ist eine Knotenliste für
6,11,2,2,3,0,3,1,4,6,1,1,2,3,5,3,2,4,5
Die Teilfolge 2,2,3 bedeutet, dass der Knoten 1 den Ausgangsgrad 2 hat und herausgehende Kanten zu den Knoten 2 und 3.
Vergleich Kanten-und Knotenliste
[Bearbeiten]Falls ein Graph mehr Kanten als Knoten hat (=„Normalfall“),benötigen Knotenlisten weniger Speicherbedarf als Kantenlisten. Das bedeutet für die Kantenlisten gilt und für die Knotenliste gilt .
Adjazenzmatrix
[Bearbeiten]Adjazenz bedeutet berühren oder aneinander grenzen. Hier werden die Graphen als Boole’sche Matrix dargestellt. 1-Einträge werden für direkte Nachbarschaften verwendet. A ist eine Adjazenzmatrix für den Graph
Beispiel
[Bearbeiten]
Eigenschaften
[Bearbeiten]Bei ungerichteten Graphen reicht eine Halbmatrix (ein Dreieck) aus. Bei gewichteten Graphen werden Gewichte statt Boolsche Werte genutzt. Der Vorteil einer Adjazenzmatrix ist, dass einige Graphenoperationen als Matrixoperation möglich sind. So ist sie beispielsweise durch iterierte Matrixmultiplikation erreichbar und besitzt schöne Eigenschaften für die mathematische Analyse.
So sieht die Darstellung als Dreiecksmatrix aus. Die Diagonale kann ebenfalls weggelassen werden, wenn Schleifen verboten sind.
Adjazenzliste
[Bearbeiten]Wir haben eine Liste der Knoten oder alternativ ein Array. Pro Knoten werden die von ihm ausgehenden Kanten als Liste, welche besonders geeignet für dünn besetzte Matrizen sind, oder als Array von Zeigern dargestellt. Der Graph wird durch |V|+1 verkettete Listen realisiert. In Adjazenzlisten sind dynamische Erweiterungen im Sinne verketteter Listen erlaubt. Knotenlisten können natürlich auch als verkettete Listen realisiert werden.

Speicherbedarf
[Bearbeiten]Seien n=|V| und m=|E|. Benötigt werden insgesamt Listenelemente. ag(i) ist die Anzahl der Nachbarn von i (gerichtet).
Transformation zwischen den Darstellungen
[Bearbeiten]Die vorgestellten Realisierungsvarianten sind äquivalent. Jede Darstellung kann in jede andere ohne Informationsverlust transformiert werden. Dafür wird die eigene Darstellung ausgelesen und anschließend die andere Darstellung erzeugt. Der Aufwand dieser Transformationen variiert von O(n+m) bis wobei im schlechtesten Fall gilt. tritt immer auf, wenn eine naive Matrixdarstellung beteiligt ist. Nicht naive Darstellungen sind für sehr dünn besetzte Matrizen nötig.
Komplexitätsbetrachtung
[Bearbeiten]Bei Kantenlisten ist das Einfügen von Kanten (Anhängen von zwei Zahlen) und von Knoten (Erhöhung der ersten Zahl um 1) besonders günstig. Das Löschen von Kanten zieht das Verschieben der nachfolgenden Kanten mit sich und die Knoten müssen neu nummeriert werden.
Bei Knotenlisten ist das Einfügen von Knoten, also die Erhöhung der ersten Zahl und das Anhängen einer 0, günstig.
Bei der Matrixdarstellung ist das Manipulieren von Kanten sehr effizient ausführbar. Der Aufwand beim Knoteneinfügen hängt von der Realisierung ab. Im worst case wird die Matrix in eine größere Matrix kopiert.
Bei Adjazenzlisten gibt es unterschiedlichen Aufwand, je nachdem, ob die Knotenliste ein Feld mit Direktzugriff oder eine verkettete Liste mit sequenziellem Durchlauf realisiert.
| Operation | Kantenliste | Knotenliste | Adjazenzmatrix | Adjazenzliste |
| Einfügen Kanten | O(1) | O(n+m) | O(1) | O(1)/O(n) |
| Löschen Kanten | O(m) | O(n+m) | O(1) | O(n) |
| Einfügen Knoten | O(1) | O(1) | O(1) | |
| Löschen Knoten | O(m) | O(n+m) | O(n+m) |
Das Löschen eines Knotens impliziert für gewöhnlich auch das Löschen der dazugehörigen Kanten.
Datenstrukturen für Graphen
[Bearbeiten]Auf dieser Seite werden die Datenstrukturen für Graphen behandelt. In Java gibt es keine hauseigene Graphimplementierung, aber es gibt diverse Pakete für verschiedene Anwendungen.
- Jung (http://jung.sourceforge.net)
Graph<Integer, String> g = new SparseMultigraph<Integer, String>();
g.addVertex((Integer)1);
g.addVertex((Integer)2);
g.addEdge("Edge1", 1, 2);
- Neo4j (http://www.neo4j.org)
GraphDatabaseService= new
"GraphDatabaseFactory().newEmbeddedDatabase(“PATH”);
Transaction tx = graphDb.beginTx();
try{
Node firstNode = graphDb.createNode();
Node secondNode = graphDb.createNode();
Relationship relationship = firstNode.createRelationshipTo(secondNode,
… );
tx.success();
}finally{
tx.finish();
}
Die allgemeine Schnittstelle für die Vorlesung ist:
public interface Graph {
public int addNode();
public boolean addEdge (int orig, int dest);
}
Implementierung Adjazenzliste
[Bearbeiten] public class AdjazenzListGraph implements Graph {
private int [][] adjacencyList=null;
//Knoten hinzufügen:
public int addNode() {
int nodeNumber = (adjacencyList ==null)?0: adjacencyList.length;
int [][] newAdjacencyList= new int [nodeNumber+1][];
//alte adjacencyList kopieren
for (int i=0; i< nodeNumber; i++)
newAdjacencyList [i]=adjacencyList[i];
//neuer Knoten hat noch keine Kanten
newAdjacencyList[nodeNumber] =null;
adjacencyList=newAdjacencyList;
return nodeNumber+1;
}
//Kante hinzufügen:
public boolean addEdge (int orig, int dest){
int nodeNumber = (adjacencyList == null)? 0: adjacencyList.length;
if (orig > nodeNumber || dest > nodeNumber || orig < 1 || dest < 1 )
return false;
if (adjacencyList[orig-1] != null)
for (int n : adjacencyList[orig-1])
//Kante bereits vorhanden?
if (n==dest) return false;
//Erste Kante am Knoten orig?
if ( adjacencyList[orig-1] == null ) {
adjacencyList [orig-1] = new int[1];
adjacencyList[orig-1][0]=dest;
}
else {
int[] newList= new int[adjacencyList[orig-1].length+1];
System.arraycopy(adjacencyList[orig-1],0,newList,0,adjacencyList[orig-1].length);
newList[adjacencyList[orig-1].length]=dest;
adjacencyList [orig-1]=newList;
}
return true;
}
}
Breitensuche
[Bearbeiten]Auf dieser Seite behandeln wir die Breitensuche. Wir fragen uns wie man die Knoten eines Graphen effizient aufzählt. Die Lösung ist der Breitendurchlauf ( Breadth-First-Search, BFS). Dabei werden die Knoten eines Graphen nach der Entfernung vom Zielknoten aufgezählt. Eine andere Methode ist der Tiefendurchlauf, zu dem kommen wir aber später. Bei dem Breitendurchlauf für ungerichtete Graphen gibt es eine Warteschlange als Zwischenspeicher. Farbmarkierungen beschreiben den Status der Knoten. Weiß bedeutet er ist unbearbeitet, grau bedeutet er ist in Bearbeitung und schwarz bedeutet, dass er abgearbeitet ist. Pro Knoten wird die Entfernung zum Startknoten berechnet. Bei der Initialisierung wird der Startknoten in eine Warteschlange eingefügt, die Farbe auf grau gesetzt und die Entfernung mit 0 berechnet. Die anderen Knoten haben eine unendliche Entfernung und sind weiß markiert.
Beim Breitendurchlauf wird der aktuelle Knoten k aus der Warteschlange genommen und schwarz gefärbt. Alle von k aus erreichbaren weißen Knoten werden grau gefärbt, die Entfernung ist der Entfernungswert von k+1 und sie werden in der Warteschlange aufgenommen.
Algorithmus
[Bearbeiten]Ergänzung zum Graph-Interface:
public interface Graph{
public int addNode();
public boolean addEdge(int orig, int dest);
public Collection<Integer> getChildren(int node);!
}
Breitendurchlauf als Iterator:
public class BfsIterator implements Iterator<Integer>{
private Graph g;
private Queue<Integer> q;
private Set<Integer> visited;
public BfsIterator(Graph g, int s){
this.g = g;
this.q = new LinkedList<Integer>();
q.add(s);
this.visited = new HashSet<Integer>();
}
public boolean hasNext() { return !this.q.isEmpty(); }
public Integer next() {
Integer n = this.q.poll();
for(Integer m: this.g.getChildren(n))
if(!this.visited.contains(m) && !this.q.contains(m))
this.q.add(m);
this.visited.add(n);
return n;
}
}
Ausgabe aller Knoten:
//Sei g ein Graph
Iterator<Integer> it = new BfsIterator(g,1);
while(it.hasNext())
System.out.println(it.next());
Analyse
[Bearbeiten]Theorem der Terminierung
[Bearbeiten]Die Breitensuche terminiert nach endlicher Zeit
Theorem der Korrektheit
[Bearbeiten]Ist G zusammenhängend, so werden alle Knoten von G genau einmal besucht.
Theorem der Laufzeit
[Bearbeiten]Ist G=(V,E) zusammenhängend und ist die Laufzeit von getChildren linear in der Anzahl der Kinder, so hat die Breitensuche eine Laufzeit von O(|V| + |E|).
Tiefendurchlauf
[Bearbeiten]Auf dieser Seite wird der Tiefendurchlauf behandelt. Der Tiefendurchlauf wird auch Depth-First-Search, oder abgekürzt DFS, genannt. Die Knoten werden aufgezählt indem vom Startknoten aus ein Pfad so weit wie möglich verfolgt wird und bei Bedarf ein Backtracking durchgeführt wird. Bei Tiefendurchlauf werden die Knoten ebenfalls farblich markiert. Weiß bedeutet der Knoten ist noch nicht bearbeitet, grau bedeutet der Knoten ist in Bearbeitung und schwarz bedeutet der Knoten ist bereits fertig abgearbeitet.
Ergänzung zum Graph Interface:
public interface Graph{
public int addNode();
public boolean addEdge(int orig, int dest);
public Collection<Integer> getChildren(int node);
public Collection<Integer> getNodes();
}
Algorithmus
[Bearbeiten]enum Color {WHITE, GRAY, BLACK};
Map<Integer,Color> color = new HashMap<Integer,Color>();
Map<Integer,Integer> pi = new HashMap<Integer,Integer>();
Map<Integer,Integer> f = new HashMap<Integer,Integer>();
Map<Integer,Integer> d = new HashMap<Integer,Integer>();
int time = 0;
color speichert die Farbe, bzw. den Bearbeitungszustand eines Knotens.
pi speichert den Vorgänger eines Knotens beim Durchlauf.
f speichert den Zeitpunkt des Bearbeitungsbeginns eines Knotens.
d speichert den Zeitpunkt des Bearbeitungsendes eines Knotens.
public void dfs(Graph g){
for(Integer n: g.getNodes())
color.put(n, Color.WHITE);
for(Integer n: g.getNodes())
if(color.get(n).equals(Color.WHITE))
dfsVisit(g,n);
}
public void dfsVisit(Graph g, Integer n){
color.put(n, Color.GRAY);
time++;
d.put(n, time);
for(Integer m: g.getChildren(n)){
if(color.get(m).equals(Color.WHITE)){
pi.put(m, n);
dfsVisit(g,m);
}
}
color.put(n, Color.BLACK);
time++;
f.put(n, time);
}
Vorgehen
[Bearbeiten]Der Tiefendurchlauf ist ein rekursiver Abstieg. Pro Knoten haben wir zwei Werte und deren Farbwerte. Beginn der Bearbeitung ist d und Ende der Bearbeitung ist f. Der rekursive Aufruf erfolgt nur bei weißen Knoten, die Terminierung der Rekursion ist hier garantiert. Die Ausführung von DFS resultiert in einer Folge von DFS-Bäumen. Der erste Baum wird aufgebaut bis keine Knoten mehr hinzugefügt werden können. Anschließend wird ein unbesuchter Knoten gewählt und fortgefahren. Bei den Kanten des aufgespannten Baumes ist der Zielknoten beim Test weiß. An den B-Kanten ist der Zielknoten beim Test grau. Hierbei handelt es sich um Back Edges oder Rückkanten im aufgespannten Baum. Eine mit B markierte Kante zeigt einen Zyklus an. Bei F Kanten werden beim Test schwarze Knoten gefunden, dessen Bearbeitungsintervall ins Intervall des aktuellen bearbeiteten Knotens passt. Es handelt sich hierbei um Forward Edges bzw. Vorwärtskanen in dem aufgespannten Baum. Bei C Kanten haben wir schwarze Zielknoten v, dessen Intervalle nicht in das aktuelle Intervall passen (d[u]>f[v]). Hierbei handelt es sich um Cross Edges, eine Kante die zwei aufgespannte Bäume verbindet.
Beispiel
[Bearbeiten]Die Notation an den Knoten ist dabei durch <Beginn der Bearbeitung d> / <Ende der Bearbeitung f> gegeben.
Analyse
[Bearbeiten]Theorem der Terminierung
[Bearbeiten]Die Tiefensuche terminiert nach endlicher Zeit.
Theorem der Korrektheit
[Bearbeiten]Es werden alle Knoten von G genau einmal besucht.
Theorem der Laufzeit
[Bearbeiten]Ist sowohl die Laufzeit von getChidlren linear in der Anzahl der Kinder als auch getNodes linear in der Anzahl der Knoten, so hat die Tiefensuche eine Laufzeit von O(|V|+|E|).
Anwendung
[Bearbeiten]Der Tiefendurchlauf wird beispielsweise bei dem Test auf Zyklenfreiheit verwendet. Damit ein Graph zyklenfrei ist, darf kein Kreis K in dem Graph G vorhanden sein. Deshalb basiert dieser Test auf dem Erkennen von Back Edges. Er ist effizienter als beispielsweise die Konstruktion einer transitiven Hülle. Die Tiefensuche wird aber auch beim topologischen Sortieren verwendet. Topologisch bedeutet sortieren nach Nachbarschaft, nicht nach totaler Ordnung.
Topologisches Sortieren
[Bearbeiten]Auf dieser Seite wird das topologische Sortieren behandelt. Wir fragen uns, wie Knoten unter Berücksichtigung von Abhängigkeiten aufgezählt werden können bei gegebenem azyklischem gerichteten Graph. Zur Anwendung kommt diese Sortierung bei Scheduling bei kausalen und zeitlichen Abhängigkeiten, zum Beispiel bei der Netzplantechnik. Mathematisch liegt hier eine Konstruktion einer totalen Ordnung aus einer Halbordnung vor.
Beispiel
[Bearbeiten]Die sorgfältige Mutter legt ihrem Kind morgens die Kleidungsstücke so auf einen Stapel, dass das Kind nur die Kleidungsstücke vom Stapel nehmen und anziehen muss und dann richtig gekleidet ist. Hierfür legt sie die Reihenfolgebedingungen fest:
Unterhose vor Hose
Hose vor Gürtel
Unterhemd vor Gürtel
Gürtel vor Pulli
Unterhemd vor Rolli
Rolli vor Pulli
Socken vor Schuhen
Hose vor Schuhen
Uhr: egal
DFS erstellt die topologische Ordnung on the fly. Das Sortieren nach f-Wert (invers) ergibt eine korrekte Reihenfolge. Statt der expliziten Sortierung nach f werden beim Setzen des f-Wertes die Knoten vorne in eine verkettete Liste eingehängt.

18 Socken
16 Unterhose
15 Hose
14 Schuhe
10 Uhr
8 Unterhemd
7 Gürtel
5 Rolli
4 Pulli
Alternativer Durchlauf:
Berechnung kürzester Wege
[Bearbeiten]Auf dieser Seite wird die Berechnung der kürzesten Wege behandelt.
Gegeben ist ein (Di-)Graph mit einer Gewichtsfunktion: . Der Pfad durch G ist eine Liste von aneinanderstoßenden Kanten . Das Gewicht oder die Länge eines Pfades ist die Aufsummierung der einzelnen Kantengewichte. . Die Distanz zweier Punkte d(u,v) ist das Gewicht des kürzesten Pfades von u nach v.
Es existieren verschiedene kürzeste Wege Probleme.
SPSP: Single pari shortest path
- Eingabe: Graph G, Startknoten s, Endknoten t
- Ausgabe: Distanz d(s,t)
SSSP: Single source shortest paths
- Eingabe: Graph G, Startknoten s
- Ausgabe: Distanzen d(s,v) für alle Knoten v
APSP: All-pairs shortest paths
- Eingabe: Graph G
- Ausgabe: Distanzen d(v,w) für alle Knoten v,w
Auf den nächsten Seiten lernen wir zwei Algorithmen zum Berechnen des kürzesten Weges kennen.
Dijkstra Algorithmus
[Bearbeiten]Auf dieser Seite wird der Dijkstra Algorithmus behandelt. Der Dijkstra Algorithmus wird zur Berechnung des kürzesten Weges benutzt (SSSP). Der Algorithmus stammt von 1959. Es erfolgt eine iterative Erweiterung einer Menge von günstig erreichbaren Knoten. Der Greedy Algorithmus hat eine ähnliche Breitensuche ist aber nur für nichtnegative Gewichte. Er berechnet iterativ verfeinert die Distanzwerte d(v,w) und es gibt eine Prioritätswarteschlange zum Herauslesen des jeweils minimalen Elements.
Priority Queues
[Bearbeiten]Eine Priority‐Queue P ist eine dynamische Datenstruktur, die (mindestens) die folgenden Operationen unterstützt:
- P.add(Element): Element hinzufügen
- P.poll(): Minimalste Element zurückgeben
- P.contains(Element): Enthält P das Element?
Die Ordnung zur Sortierung muss dabei vorab definiert sein.
Ein Heap kann beispielsweise zur Implementierung einer Priority‐Queue benutzt werden (add‐Operation ist dann O(log n), poll‐Operation O(log n), und contains‐Operation ist O(n)). Benutzt man zusätzlich zum Heap noch einen binären Suchbaum auf denselben Element so ist auch contains in O(log n) realisierbar.
Priority Queue in Java
[Bearbeiten]class DijkstraComparator implements Comparator<Integer>{
Map<Integer,Integer> d = new HashMap<Integer,Integer>();
public DijComparator(Map<Integer,Integer> d){
this.d = d;
}
public int compare(Integer o1, Integer o2) {
return d.get(o1).compareTo(d.get(o2));
}
}
Ist d eine Map “Knoten”‐>”Aktueller Distanzwert von s aus”, so ist PriorityQueue<Integer> queue = new PriorityQueue<Integer>(g.getNumberOfNodes(),new DijkstraComparator(d)); eine Priority‐Queue, die bei iterativen Aufruf queue.poll() immer das Element mit dem minimalsten d‐Wert zurückliefert.
Idee
[Bearbeiten]- Initialisiere alle Distanzwerte von s zu v mit ∞ (und von s zu s mit 0)
- Initialisiere eine Priority‐Queue Q mit allen v
- Extrahiere das minimale Element aus Q
- Aktualisiere alle Distanzwerte der Nachfolger von in Q:
- Ist es günstiger über zu einem Knoten w zu kommen?
- Falls ja setzte d(s,w)=d(s,)+y(,w)
- 5. Wiederhole bei 3 solange Q noch Elemente hat
Algorithmus in Java
[Bearbeiten]Map<Integer,Integer> dijkstra(Graph g, int s){
Map<Integer,Integer> d = new HashMap<Integer, Integer>();
PriorityQueue<Integer> queue = //Initialisiere Priority-Queue entsprechend
for(Integer n: g){
if(!n.equals(s)){
d.put(n, Integer.MAX_VALUE);
queue.add(n);
}
}
d.put(s, 0);
queue.add(s);
while(!queue.isEmpty()){
Integer u = queue.poll();
for(Integer v: g.getChildren(u)){
if(queue.contains(v)){
if(d.get(u) + g.getWeight(u,v) < d.get(v){
d.put(v, d.get(u) + g.getWeight(u,v));
}
}
}
}
return d;
}
Algorithmus
[Bearbeiten]algorithm Dijkstra (G,s)
- Eingabe: Graph G mit Startknoten s
- for each Knoten u V[G] -s do // Initialisierung
- D[u] :=
- od;
- D[s]:= O; PriorityQueue Q := V;
- while not isEmpty (Q) do
- U := extractMinimal (Q);
- for each v ZielknotenAusgehenderKanten (u) Q do
- if D[u] + ((u,v)) < D[v] then // Entfernung über u nach v kleiner als aktuelle Entfernung D[v]
- D[v] := D[u] + ((u,v));
- adjustiere Q an neuen Wert D[v]
- fi
- if D[u] + ((u,v)) < D[v] then // Entfernung über u nach v kleiner als aktuelle Entfernung D[v]
- od
- od
- for each Knoten u V[G] -s do // Initialisierung
Initialisierung
[Bearbeiten]

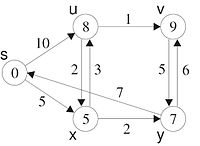
Der Iterationsstart ist korrekt für die Tiefe 0. Wir nehmen an, dass der vorherige Iterationsschritt korrekt war ( Induktionsbeweis). Der Ein Iterationsschritt ist jeweils die günstigste Verbindung zu einem noch nicht bearbeiteten Knoten hinzunehmen. Da die bisher bearbeiteten Knoten den korrekten Distanzwert haben, ist der neue Distanzwert durch den „günstigsten“ aus dem bisher bearbeiteten Teilgraphen um genau eine Kante hinausgehenden Pfad bestimmt. Jeder Pfad zum Zielknoten dieses Pfades, der um mehr als eine Kante aus dem bearbeiteten Bereich hinausgeht, ist teurer als die gewählte, da Kosten mit zusätzlich hinzu genommenen Kanten nicht sinken können.
Analyse
[Bearbeiten]Terminierungstheorem
[Bearbeiten]Der Algorithmus von Dijkstra terminiert für eine endliche Eingabe nach endlicher Zeit.
Beweis
[Bearbeiten]In jedem Schritt der while‐Schleife wird ein Element aus queue entfernt und die Schleife endet sobald queue leer ist. Jeder Knoten hat nur endliche viele Kinder, deswegen ist auch die Laufzeit der inneren for‐Schleife endlich.
Korrektheitstheorem
[Bearbeiten]Sind alle Kantengewichte nicht‐negativ, so enthält d am Ende die Distanzwerte von s zu allen anderen Knoten.
Beweis
[Bearbeiten]Beachte, dass sobald ein Knoten v aus queue entfernt wird, der Wert für v in d nicht mehr geändert wird.
Zeige nun, dass gilt: Wird v aus queue entfernt, so enthält d den Distanzwert von s nach v. Zeige dies durch Induktion nach i=„Anzahl bisher aus queue entfernter Knoten“:
- i=0: Am Anfang hat queue nur für s einen endlichen Wert gespeichert, alle anderen Werte sind ∞. Der Knoten s wird auch stets zuerst entfernt und der Distanzwert ist 0. Dies ist auch korrekt, da s zu sich selbst Distanz 0 hat und alle anderen Knoten keine geringere Distanz von s aus haben können (da alle Kanten nicht‐negative Gewichte haben).
- i → i+1: Sei v der (i+1)te Knoten, der aus queue entfernt wird.
- Da die bisher bearbeiteten Knoten den korrekten Distanzwert haben, ist der neue Distanzwert durch den „günstigsten“ aus dem bisher bearbeiteten Teilgraphen um genau eine Kante hinausgehenden Pfad bestimmt.
- Jeder Pfad zum Zielknoten dieses Pfades, der um mehr als eine Kante aus dem bearbeiteten Bereich hinausgeht, ist teurer als die gewählte, da Kosten mit zusätzlich hinzugenommenen Kanten nicht sinken können.
Laufzeittheorem
[Bearbeiten]Sei G=(V,E,g) ein gerichteter Graph. Der Laufzeitaufwand von Dijkstras Algorithmus für einen beliebigen Knoten s in G ist O((|E| + |V|) log |V|).
Beweis
[Bearbeiten]Beachte: Wird für die Priority‐Queue beispielsweise ein Heap verwendet, so hat die Operation poll() einen Aufwand von O(log k) (mit k=„Anzahl Elemente in Queue“). Sei |V|=n und |E|=m. Insgesamt: O(n log n) + O(n) + n* O(log n) + m *O(log n) = O((m + n) log n) Durch Benutzung sog. Fibonacci‐Heaps (anstatt normaler Heaps) kann die Laufzeit von O((m + n) log n) verbessert werden zu O(m + n log n)
Nachteile
[Bearbeiten]Der kürzeste Weg wird immer gefunden, aber es werden viele unnötige und sinnlose Wege gegangen. Bei negativen Kanten resultieren auch falsche Ergebnisse.
Spannbäume
[Bearbeiten]Auf dieser Seite werden Spannbäume und in diesem Zusammenhang der Algorithmus von Prim behandelt.
Beispiel Kommunikationsnetz
[Bearbeiten]Zwischen n Knotenpunkten soll ein möglichst billiges Kommunikationsnetz geschaltet werden, so dass jeder Knotenpunkt mit jedem anderen verbunden ist, ggf. auf einem Umweg über andere Knotenpunkte. Bekannt sind die Kosten für die direkte Verbindung zwischen und . Alle Kosten seien verschieden und größer Null. Die Modellierung geschieht somit als gewichteter, ungerichteter und vollständiger Graph mit einer Gewichtungsfunktion c.

etc; abgekürzt etc
Problemstellung: Finde minimal aufspannenden Baum
[Bearbeiten]Einige Definitionen für ungerichtete Graphen:
Ein Graph G=(V,E) heißt zusammenhängend, wenn für alle v,w∈V ein Pfad von v nach w in G existiert.
Ein Graph G=(V,E) enthält einen Zyklus, wenn es unterschiedliche Knoten gibt, so dass . Ein Graph G=(V,E) heißt Baum, wenn er zusammenhängend ist und keinen Zyklus enthält.
Ein Graph G’=(V’,E’) heißt Teilgraph von G=(V,E), wenn und .
Ein Graph G’=(V’,E’) heißt induzierter Teilgraph von G=(V,E) bzgl. , wenn
Ein Graph G‘=(V‘,E‘) heißt Spannbaum von G=(V,E), wenn V'=V und G' ein Teilgraph von G und ein Baum ist.
Das Gewicht einen Graphen G=(V,E) ist .
Ein Graph G'=(V',E') ist ein minimaler Spannbaum von G=(V,E), wenn G' ein Spannbaum von G ist und G' unter allen Spannbäumen von G das minimalste Gewicht hat.





















![{\displaystyle i\in \{0,...,n-1\}~mit~b=A[i]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a71db61f40cc4120f56376913b0d03b8d4bc95a)






























































































































































































































































































































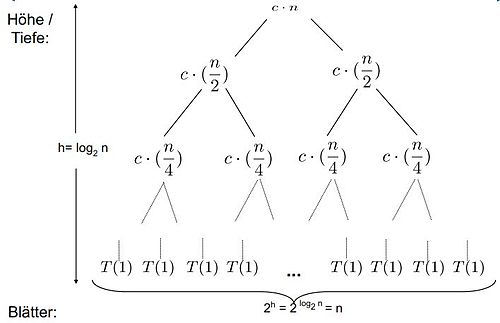
















































![{\displaystyle p\in [u,o]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dbbbbffbc252be70b64e3ebca2b391ae5bd24b19)






























































































































































![{\displaystyle D[s]+\gamma (s,u)<D[u]?}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c738ddab1c09a24b922d405a821a042339ef1317)

![{\displaystyle \Rightarrow D[u]=10}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71317c99dbf3d74df30200ee1693f2f3b3b427b5)
![{\displaystyle D[s]+\gamma (s,x)<D[x]?}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1f379f2308dd6ac3b8764fb38919f07e18d61eb)

![{\displaystyle \Rightarrow D[x]=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1b4a0320223418c33a7338081e03f0a4141161)

![{\displaystyle D[x]+\gamma (x,u)<D[u]?}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d4556cb5d2c3bfc966d2ef2ced8ce1efc25af76)

![{\displaystyle \Rightarrow D[u]=8}](https://wikimedia.org/api/rest_v1/media/math/render/svg/331ce6731fa686c7b80487c3ac7454ab4eaa772a)
![{\displaystyle D[y]analog}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c32c7936bdfff2c96f467e84db2fc70c86592a)
















