Kurs:Herxheimer Modell

Einführung unseres Modells (Herxheim 2020)

Folgend werden wir unser selbsterstelltes SIR-Modell zusammen mit/ für SuS mithilfe einer Tabellenkalkulation programmmieren. Die Wahl fiel auf diesen Programmtyp, da hier die Mathematik hinter einer Pandemie nicht über die Grundrechenarten hinausgeht und somit das komplexe Thema schüler*innengerecht veranschaulicht und erarbeitet werden kann. Die Tabellenkalkulation ermöglicht es schließlich, mit verschiedenen Paramametern zu spielen und somit deren Auswirkungen auf den Verlauf der Pandemie graphisch sichtbar zu machen. Mit dieser spielerischen Herangehensweise soll bei den SUS nicht nur die Motivation gesteigert werden, gleichzeitig wird auch Elementares zu dem Verlauf von Pandemien, ihrer Einflussfaktoren und der Umgang mit Tabellenkalkulationsprogrammen geschult. Dies würde sich beispielsweise für einen fächerübergreifenden Unterricht in Nawi, Mathematik, Gesundheit und/ oder Informatik anbieten.

Aufbauend auf dem SIR, dass neben den Empfänglichen, Infizierten und Genesenen nun auch die Verstorbenen und Geimpften miteinschließt, wurde zunächst überlegt, welche "Töpfe" benötigt werden und welchen Weg die Individuen der Bevölkerung innerhalb des Modells gehen können.

Da sich unsere Schule in Herxheim befindet, berechnen wir unser Modell mit der dortlebenden Einwohnerzahl (10.000 Menschen) für genau 1 Jahr. Am 1. Tag der Pandemie (15.01.2020) kerte ein Herxheimer coronainfiziert vom Ischgel-Urlaub zurück in seine Heimat. Zu diesem Zeitpunkt waren alle übrigen 9.999 Bewewohner noch gesund - somit empfänglich für die neue Krankheit. Es gab weder Genesene noch Verstorbene, auch ein Impfstoff stand noch nicht zur Verfügung.

Code

Nun werden nach und nach die Pfeile "mit Inhalt" gefüllt. Dabei stand folgende Frage im Raum: Wie lassen sich Formeln angeben, mit denen die weiteren Zeilen jeweils berechnen werden können. Wie die jeweiligen Pfeile nachher berechnet werden, findet ihr in diesem Kapitel in der dazugehörigen Farbe.

Vor der Berechnung mussten wir in einem ersten Schritt fixe Parameter festlegen, die durch den Virustyp bedingt sind:

• Infektionsgeschwindigkeit/-rate = 0,004 (dahinter steckt beispielweise, wie schnell sich das Virus verbreitet oder wie viele Kontakte man trifft und somit potenziell anstecken könnte - diese Rate kann auch variieren, wenn eine neue Virusmutation ansteckender ist, wie z.B. die britische Mutation)
• Genesungsrate = 0,1 (1 geteilt durch Dauer der Infektion, in diesem Fall 1/10, also wie viele Infizierte von dem Virus nach einer gewissen Zeit genesen sind)
• Sterberate = 0,02 (Wie viele der Infizierten Sterben an der Krankheit? Zu Beginn einer Pandemie nicht vorherzusagen, in der Realität stark Individuumsabhängig)

Jetzt werden die Einträge des 2. Tages Schritt für Schritt erarbeitet. Stehen alle Formeln fest (farbige Einträge, siehe Pfeile oben), können diese für das komplette Jahr übertragen werden. Beginnen wir mit dem Feld der Empfänglichen am 16.01.2020. Dieser Eintrag errechnet sich durch den Wert des Vortags (+B2) abzüglich derer, die sich neu Infizieren (-B2*C2*Infektionsrate). Die Personen, die wir abgezogen haben, müssen ins Feld der Infizierten mitaufgenommen (+B2*C2*Infektionsrate) und mit der Anzahl der Vortagsinfizierten addiert werden (+C2). In die Gruppe der Infizierten kommen jedoch nicht nur neue Personen hinzu, die Genesenen verlassen diese auch wieder (-Genesungsrate*C2) (Vortagsinfizierte multipliziert mit der Wahrscheinlichkeit zu genesen). Die gerade abgezogenen Personen wandern ins Feld der Imunen/ Genesenen (+Genesungsrate*C2) und werden mit den Vortagsgenesenen addiert (+D2). Aus der Gruppe der Infizierten, werden außerdem jene abgezogen, die an der Krankheit versterben (-Sterberate*C2) (Wahrscheinlichekit zu sterben multipliziert mit den Vortagsinfizierten). Diese werden ins Feld der Gestorbenen aufgenommen (+Sterberate*C2). Infizieren sich an einem Tag mehr Menschen als jede, die sterben bzw. genesen, steigt die Anzahl der aktuell Infizierten, andernfalls sinkt sie. .
Nun werden gewisse Schuzmaßnahmen miteinbezogen, die die Verbreitung der Pandmie verlangsamen können (Lockdown/ FFP2-Masken). Dies gelingt, in den wir die Gruppe der Infizierten mit der Basisreproduktionszahl multipizieren. Dieser Wert ist jedoch nicht fest, sondern ändert sich im Laufe des Geschehens. Werden beispielsweise Kontaktbeschränkungen, Masken oder Quarantäne verordnet, verringert sie sich. Mutiert allerdings das Virus und wird übertragbarer, steigt die BRZ über das Ausgangsniveau.
Als letzten Schritt wollen wir in das Geschehen Impfungen einbeziehen. Von den Empfänglichen wandert dabei täglich eine festgelegte Antahl an Personen (-Impfungen/Tag) in die Gruppe der Geimpften (+Impfungen/Tag). Wir gehen davon aus, dass ledlich die noch Empfänglichen geimpft werden und nicht bereits infizierte/genesene. Da jedoch nicht bereits am 1. Tag Impfschutz besteht, werden nur die abgezogen, die vor genau einer Woche geimpft wurden. Unserer Annahme nach sind diese Personen dann immun, werden nicht mehr infiziert und werden quasi mit den Genesenen gleichgesetzt. Da allerdings noch nicht gleich zu Beginn der Pandmie ein Impfstoff zur verfügung steht, entscheiden wir uns, die Impfkampange genau nach einem halben Jahr (15.07) starten zu lassen.

Die fertige Datei kann hier aufgerufen werden: https://www.file-upload.net/download-14587716/EigenesModelmitversch.BRZ.ods.html

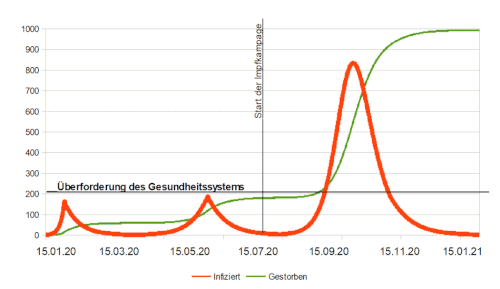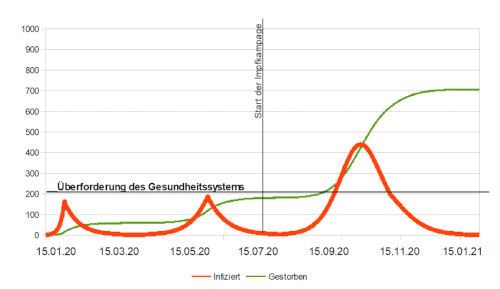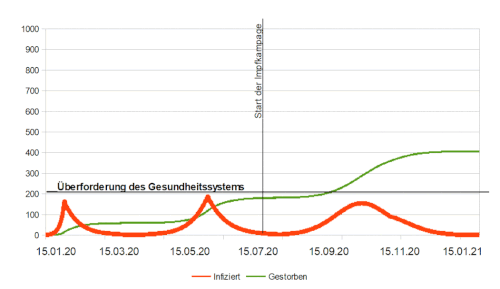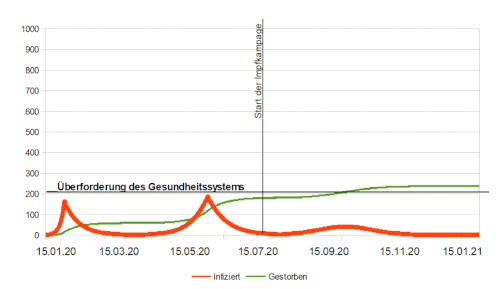
1. Zyklus: Pandemisches geschehen ohne eingreifende Maßnahmen

Die Intensivstation des Herxheimer Krankenhaus hat eine Kapazität von 20 Betten. Wir gehen im Folgenden davon aus, dass 10% der aktuell Infizierten auf der Intensivstation behandelt werden müssen. Würden wird unser Verhalten nicht ändern, würde die Pandemie folgendermaßen verlaufen:

Interpretation

Diese Simulation hätte einen enormen Anstieg der Infizierten und Toten zur Folge. Der Höhepunkt der Pandemie, der steilste Anstieg der Kurve der Infizierten/stärkster Zuwachs der Infizierten, trifft zeitlich früh ein und das pandemische Geschehen entspannt sich anschließend wieder. Dieser Verlauf würde allerdings schnell zur Überlastung des Gesundheitssystems führen, da man zwischenzeitlich über 400 Betten brauchen würde. Über 40% der Bevölkerung sind zweitweise gleichzeitig infiziert und fast alle Bewohner hätten bereits nach 3 Monaten die Infektion durchgemacht, d.h. sind entweder infiziert, immun auf Grund einer vorherigen Infektion oder verstorben.
Die Anzahl der Toten beträgt mit knapp 2.000 fast 1/5 der gesamten Bevölkerung. Der einzige Vorteil dieses Vorgehens wäre, dass das pandemische Geschehen bereits zum 01.April weitgehend zum Erliegen gekommen wäre, da die Bevölkerung bereits "gesättigt" ist, also die pandemische Situation sich durch die Herdenimmunität entspannt. In der 2. Jahreshälfte ändern sich die Werte dann (fast) gar nicht mehr. Allergings wären die gesellschaftlichen Auswirkungen katastrophal, sodass davon ausgegangen werden kann, dass niemand diesen Verlauf in Kauf nehmen möchte. Zu Bedenken bleibt auch, dass die Immunität von bereits Genesenen nicht auf Dauer ist und diese nach einiger Zeit erneut anfällig für neue Infektionen werden, die pandemische Situation sich also wiederholen könnte. Zudem "versucht" das Virus langfristig zu überleben, indem es mutiert und gegebenenfalls schneller bereits Genesene infizieren oder ansteckender sein kann.

2. Zyklus: Pandemisches geschehen inkl. eingreifender Maßnahmen bzw. Virusvariante

Im Folgenden wird unter beibehaltener Infektios-, Sterbe- und Genesungsrate die neue Situation modelliert, dass sich die BRZ ändert. Dies geschieht beispielsweise durch einen Lockdown, das Tragen von Masken (BRZ fällt) oder einer ansteckenderen Virusvariante (BRZ steigt).

Diese Simulation beinhaltet folgende einschneidende Veränderungen:

• 2 x Lockdown
• mutierte Virusvariante

Interpretation

Mit einschneidenden Maßnahmen konnte die Anzahl der Toten auf 1000 halbiert werden. Wie schnell die Kurve der Infizierten abflacht, hängt dabei von der Wahl der Maßnahmen und ihrer Dauer ab. Es wird deutlich, wie schnell der Erfolg eines Lockdowns nach der Lockerung wieder verschwindet, wenn die Bevölkerung noch zum Teil empfänglich für die Krankheit ist. Es werden hier innerhalb des Jahres drei "Wellen" durchlaufen. Die ersten beiden wurden jeweils durch einen Lockdown gebrochen. Die dritte Welle wurde erst durch die Sättigung der Anfälligen beendet. In einem nächsten Schritt soll versucht werden die dritte Welle ohne einen Lockdown, bspw. mit der Hilfe von Impfungen, zu verhindern.

Durch die simulierte ansteckendere Virusvariante käme es nämlich trotz vorheriger Einschränkungen erneut zur Überlastung des Gesundheitssystems.

3. Zyklus: Animation einer (linearen) Impfkampange

Folgende Simulation behält die vorherigen Lockdownmaßnahmen und die ansteckendere Virusmutante bei. Allerdings wird das Modell um das Hilfmittel des Impfens erweitert. Pro Tag werden eine festgelegte Anzahl an Personen geimpft und von der Gruppe der Empfänglichen abgezogen. Durch die täglichen Impfungen wird Einfluss auf das pandemische Geschehen genommen. Dabei kann der Impfstart forschungsbedingt zeitlich nicht nach vorne gelegt werden, lediglich die Produktion und Verimpfung pro Tag ist variierbar und wird in folgenden GIFS veranschaulicht. Links ist unser gesamtes Modell abgebildet. Rechts werden aus dem Modell zur besseren Veranschaulichung wieder nur die Infizierten und Toten angezeigt.

Interpretation

Die einsetztende Impfkampange hat keinen Einfluss mehr auf die zweite Welle, da diese zum Impfstart bereits abgeklungen ist. Allerdings wirken sich die Impfungen stark auf die dritte Welle aus. Durch die Impfung fällt die Anzahl der potentiell Empfänglichen stark ab (zum Jahresende kaum empfängliche = Herdenimunität). Die dritte Welle (durch Virusmutante) fällt dabei umso geringer aus, je mehr Personen täglich geimpft werden kann. Sie kann mit ausreichend Impfstoff sogar komplett vermieden werden, wodurch sich auch die Anzahl der Toten kaum noch erhöht (ohne Impfung 1000 Tote, mit 36 Impfungen pro Tag nur 200 Tote). Erkennbar wird auch, dass viel weniger Personen der Bevölkerung die Infektion überhaupt durchmachen müssen und somit Langzeitfolgen nach Genesung, mögliche Long Covid Fälle, vermieden werden können. Als Fazit könnte man festhalten, dass möglichst viel Impfstoff schnell zur Verfügung stehen sollte, denn der positive Einfluss auf das Geschehen kann bei ausreichender Anzahl an Impfdosen enorm sein. Es sollte unbürokratisch und pragmatisch gehandelt werden, Geld keine Rolle spielen, denn die Impfung ist während der Pandemie ein wahrer "Gamechanger". Mit genügend Impfstoff würde in dieser Sumulation sogar das Gesundheitssystem nicht überlastet werden und die Kapazität der Intensivbetten ausreichend sein.

4. Zyklus: Optimierung der Impfkampagne

Eigentlich wäre unsere Modelierung hier am Ende, denn innerhalb des letzten Zykluses wird dem Model nichts mehr neues hinzugeführt. Lediglich bisherig Erarbeitetes wird verfeinert. Der positive Einfluss der Impfungen wurde im 3. Zyklus bereits gezeigt, daran ändert sich auch nichts mehr. Der Verlauf der Impfungen wird lediglich optimiert und der Realität angepasst. Dies geschieht in zwei aufeinaner aufbauenden Teilen.

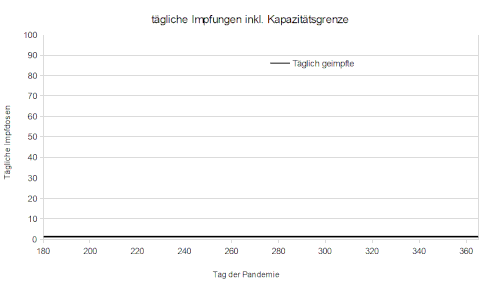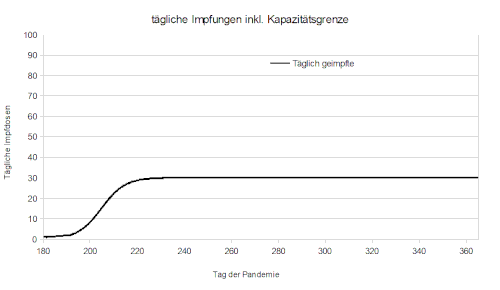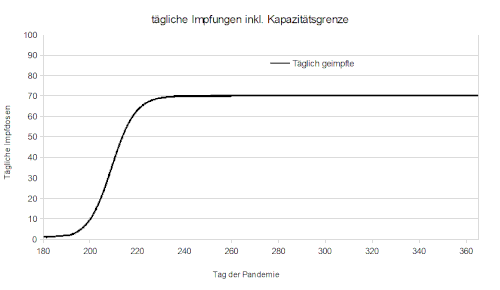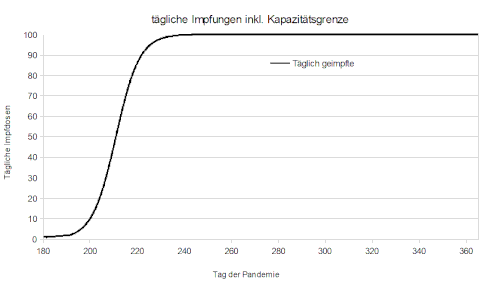
1. Teil: beschränktes Wachstum der Impfungen

Der Ablauf der Impfkampange aus Zyklus 3 stimmt nämlich nicht mit den Erfahrungen aus der Realität überein. Modelliert wurde, dass die Anzahl der täglich verabreichten Dosen an jedem Tag der Kampange gleich hoch ist. Die Realität sieht aber so aus, dass vor allem zu Beginn sehr wenig Impfstoff zur verfügung steht. Erst nach und nach werden Kapazitäten aufgebaut, mehr Lieferungen treffen ein, neue Impfstoffe kommen auf den Markt und nachdem anfänglich nur die Impfzentren beteiligt waren, steigen nach und nach immer mehr Hausärzte mit ein. Folglich steigt aucch die Anzahl der täglichen Impfungen. Jedoch liegt kein unbeschränktes Wachstum vor, es gibt eine natürliche Kapazitätsgrenze. Diese könnte bedingt sein durch freies Personal oder die maximal gelieferten Mengen. Wir haben unser Modell dahingehend optimiert, dass am 1. Tag der Impfkampange (t=1) lediglich eine Dose verabreicht wurde, die Kapazitätsgrenze liegt bei 100 Impfungen/Tag. Die logistische Funktion (tägliche Impfungen) die wir erstelt hatten lautet: 100/1+99*e^0,8*t. Verschiedene Kapazitätsgrenzen wurden im Folgenden simuliert und grafisch dargestellt.

Änderung des Codes

Den oben beschriebenen Code (Kapitel 3.2.2) mussten wir für dieses Vorgehen etwas anpassen. Die bisherigen Spalten der täglischen bzw. kumulierten Impfungen wurden dafür neu geschrieben. Im Feld der taglichen Impfugen steht dabei die logistische Funktion. Die Kapazitätsgrenze (Zähler der Formel) steht dabei seperat in einem extra Feld, damit diese variabel gehandhabt werden kann. Für das t in der Formel wurde der jeweile Tag der Imppfkampange eingesetzt (also am 4. Tag der Impfkampange ist t=4). Somit erhalten wir im Laufe der Zeit den Grafen der logistischen Funktion.

Interpretation

Auch hier hat die Impfung natürlich einen positiven Effekt auf den Verlauf der Pandemie. Unterschied zum linearen Impfverlauf im 3. Zyklus ist nun aber, dass die Impfugen zu Beginn der Kampange noch relativ wenig Einfluss haben. Dies erklärt sich damit, dass die logistische Funktion bei kleinen x-Werten auch realtiv niedrig ist. Erst mit zunehmender Zeit nimmt die Kampage an Fahrt auf und die Impfzahlen nehmen deutlich Einfluss auf die Anzahl der Infizierten/ Toten.

2. Teil: Differenzierung zwischen Erst- und Zweitumpfungen

Bisher haben wir außer Acht gelassen, dass fast alle Impfstoffe für ihre vollständigen Wirkung zwei Mal verabreicht werden müssen. Auch dafür mussten wir den Code erneut anpassen, da nun zwischen Erst- und Zweitimpfungen unterschieden werden soll. Für die Erstimpfung haben wir die gleiche Funktion benutzt, wie im Teil 1. Wir gehen nun davon aus, dann nach der 1. Impfung nur ein Teilschutz besteht. Wie hoch dieser Prozentsatz ist, lässt sich aus der Literatur nichterkennen. Es wird lediglich berichtet, um wie viel % die Wahrscheinlichekit gesenkt wird, "schwer" an Covid zu erkranken. Es fehlt allerdings, um wie viel Prozent das Risiko gesenkt wird, sich überhaupt anzustecken. Deshalb schätzen wir den Prozentsatz aus dem (Bauch heraus) auf 60%.
Die Funktion der Zweitimpfungen verläuft genau wie die der Erstimpfungen, lediglich 4 Wochen (28 Tage) verzögert. Wir gehen also davon aus, dass alle Erstgeimpften 4 Wochen später zur Zweitimpfung terminiert werden. Diese Impfung senkt das Risiko einer Infektion nun um weitere 30%. Somit hat eine Person nach ihrer Zweitipfung einen Schutz von 90%. Wir ziehen die Geimoften dabei wieder im Abstand von jeweils einer Woche von den Empfänglichen ab, da wir davon ausgehen, dass das Imunsystem eine Tage benötigt, um auf den Impfstoff zu reagieren. In unserem Modell wirkt sich das vollgendermaßen aus: Von 100 zweitgeipmften Personen fallen 7 Tage später insgemant 90 aus dem Topf der "Empfänglichen" raus. Bei den restlichen 10% hat entweder der Körper keine bzw. nicht ausreichend Antikörper gebieldet oder der Geimpfte hatte die Infektion bereits hinter sich und zählte somit bereits nicht mehr zu den Empfänglichen.
Dieses Vorgehen sorgt dafür, dass eine einzelne Person nun nicht mehr genau fest einem "Topf" zugeordnert werden kann, sondern neue Zwischenräume entstehen. Eine Person kann somit teilweise zwei verschiedenen Gruppen zugeordnet werdeb. Dies soll an ahand einer Beispielperon bzgl. seines Impfstatuses in folgender Tabelle veranschaulicht werden.

Impfstatus einer Person inkl. seiner Zuordnung

Status	Empfänglich	Imun
ohne Impfung	1	0
7 Tage nach 1. Impfung	0,4	0,6
7 Tage nach 2. Impfung	0,1	0,9

Ausblick 5. Zyklus (für die kommende Generation an Mathematik-Studierende)

In einem 5. Zyklus könnte man nun den Verlust der erworbenen Imunität in das Modell miteinbeziehen. Aktueller Stand der Forchung ist es, dass sowohl Genesenen als auch Geimmpfte nach mehreren Monaten zumindest einen Teil ihrer Imunität wieder einbüsen. Dies würde dafür sorgen, dass vom Topf der Genesenen und der Geimpften ein Teil wieder zurück in den Topf der "Empfänglichen" wandern würde. Diesen Schritt könnten Studierende in den noch folgenden Semestern modellieren, wenn dazu bessere Daten zur Verfügung stehen.