Kurs:Visualisieren

Projekt
Projekttitel	Visualisieren
Ansprechpartner	Klaus-Dieter Keller
Laufzeit	1 Schulstunde während der Projektphase I
Kurzbeschreibung
Einheit der Methodentage der 11. Klassen des Margarete-Steiff-Gymnasiums Giengen

Visualisieren ist eine der fünf Einheiten der Methodentage der 11. Klassen, insgesamt gibt es:

Präsentieren
Zitieren
Visualisieren
Rhetorik
Urheberrecht

Vorbereitung[Bearbeiten]

Die Lehrkraft benötigt einen Raum mit Laptop und Beamer. Es wird empfohlen, auf diesem Laptop nur die Bilder zu zeigen (ein Bild pro Tab im Browser öffnen) und auf einem zweiten Gerät (Tablet, Smartphone) diese Übersicht geöffnet zu haben.

Einstieg[Bearbeiten]

Visualisieren nennt man die grafische Veranschaulichung von Daten und Zusammenhängen. In diesen 45 Minuten gehen wir auf zwei Aspekte ein, die aus Schülersicht interessant sind:

Wie visualisiert man Daten für eine Präsentation/GFS?
Wie wird mit Diagrammen „gelogen“?

Visualisieren von Daten für Präsentationen[Bearbeiten]

Ein Bild sagt mehr als tausend Worte. In Visualisierungen lassen sich Verläufe, Maximalwerte, Trends und Zusammenhänge viel schneller erkennen. Es gibt mehrere Möglichkeiten, Diagramme zu erstellen. Sie werden hier vorgestellt.

x-y-Diagramm und Liniendiagramm[Bearbeiten]

x-y-Diagramm
Das direkte Verbinden dieser Punkte ist sinnlos.
x-y-Diagramm mit Inter- und Extrapolation
Bei gleichen Punkten sind verschiedene Ausgleichsfunktionen möglich.

Verbindet man die Punkte eines x-y-Diagramms (engl. dot plot), erhält man ein Liniendiagramm. Dies ist jedoch nicht immer sinnvoll, denn oft sind dazwischenliegende Wertepaare vielleicht nicht bekannt und es gäbe durch weitere Punkte einen anderen Linienverlauf.

„Wahre“ Liniendiagramme gibt es nur bei bekannter Abhängigkeit der zwei Größen, z.B. durch eine Formel/Funktion.

Man sollte im Normalfall bei x-y-Diagrammen keine Linie einzeichnen. Ist die Abhängigkeit naheliegend, kann ein Funktionsgraph zwischen den Werten (Interpolation) oder über die bekannten Werte hinaus (Extrapolation) eingezeichnet werden. Bekannte Extrapolationen sind z.B. Wahl-Hochrechnungen oder Wetterberichte.

Falls man ein Liniendiagramm als Ausgleichsfunktion aus Punkten erstellt, muss man die Punkte deutlich eingezeichnet lassen.

Säulendiagramm[Bearbeiten]

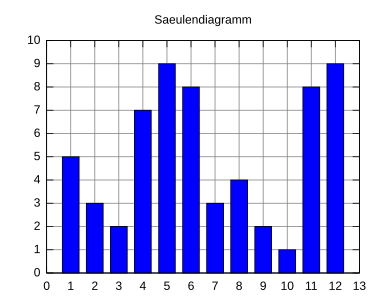
Säulendiagramm
gestapeltes Säulendiagramm, hier in Prozent

Balkendiagramm[Bearbeiten]

Bei Balkendiagrammen werden aus den vertikalen Säulen horizontale Balken. Mit ihnen können Rangfolgen gut dargestellt werden.

Kreisdiagramm[Bearbeiten]

Kreisdiagramme/Tortendiagramme können mit den absoluten Werten oder den Prozentwerten beschriftet werden.

Tipps[Bearbeiten]

Die dreidimensionale Darstellung bei allen Diagrammarten verfälscht die Aussagen und erschwert es, Daten abzulesen.
Bei Säulen und Hintergründen nicht mit Farbverläufen arbeiten. Das lenkt ab.

Wie wird mit Diagrammen „gelogen“?[Bearbeiten]

Auswahl der dargestellten Bereiche[Bearbeiten]

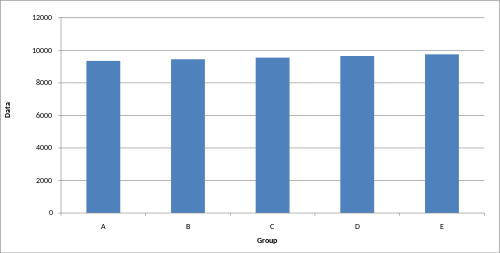
Das Diagramm sieht nach einer starken Zunahme aus, weil die y-Achse nicht bei 0 startet.
Hier die gleichen Zahlenwerte; sie bleiben nahezu konstant.

Skalierung der Achsen[Bearbeiten]

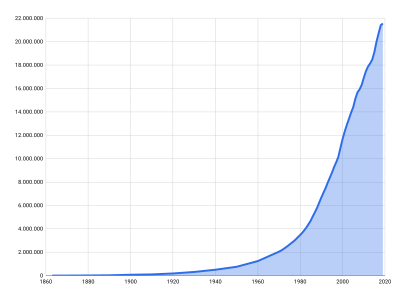
Hier wurde für die y-Achse eine logarithmische Skala gewählt. Der Anstieg erscheint dadurch kleiner als er ist.
Die „Wahrheit“ mit den gleichen Daten: Mit der linearen Skala ist der Anstieg viel größer.

Mit der logarithmischen Skala erscheint exponentielles Wachstum als eine Gerade.

Perspektive[Bearbeiten]

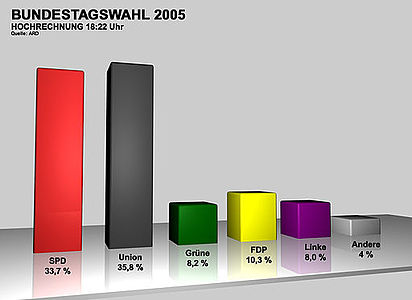
dreidimensionales Balkendiagramm: die Werte erscheinen verzerrt, Ablesen und Vergleichen ist erschwert
Spiegelungen lassen die Säulen noch größer erscheinen, aber nicht gleichmäßig mehr
dreidimensionales Kreisdiagramm: vorne erscheinen die Tortenstücke größer als hinten, wenn der Rand auch die Farbe des Tortenstückes hat

dreidimensionales Kreisdiagramm: Tortenstücke links und rechts erscheinen viel größer, weil sie mehr Fläche einnehmen

evtl. Live Demo mit LibreOffice Calc

Kreise im Diagramm[Bearbeiten]

Frage zum Schluss: Welches der Diagramme visualisiert die Zahlen „ehrlicher“ und warum?

Antwort: Im ersten Diagramm steckt die Variable im Durchmesser (also der Höhe) der Kreise, im zweiten Diagramm im Flächeninhalt. „Ehrlicher“ ist das zweite Diagramm, weil der Flächeninhalt der Kugel 10 dort drei Mal in die Kugel 30 passt. Im ersten Diagramm passt die Kugel 10 neun Mal in die Kugel 30.