Kurs:Wirtschaftsinformatik WS08 09 PROGRAMMIERUNG/Ausgangstest
Aufgabe 1
[Bearbeiten]1. Implementieren Sie eine Methode, die alle Zahlen von 1 bis zu einer definierten Zahl n addiert. Beispiel addiere(3) addiert 1 + 2 + 3 = 6
Zur Lösung dieser Aufgabe können Sie die Datei addieren.java verwenden.
Aufgabe 2
[Bearbeiten]2. Implementieren Sie eine Methode, die als Eingabe einen beliebigen String s und ein Zeichen z erhält. Aufgabe der Methode ist es, zu zählen, wie oft das Zeichen z im String s enthalten ist. Beim Vergleichen ist auf Groß/Kleinschreibung zu achten.
Zur Lösung dieser Aufgabe können Sie die Datei zaehlen.java verwenden.
Aufgabe 3
[Bearbeiten]3. Implementieren Sie eine Methode, die als Eingabe zwei Strings s1 und s2 enthält. Sie dürfen annehmen, dass s1 länger ist als s2. Die Methode soll überprüfen, ob der String s2 im String s1 enthalten ist. Hierbei ist auf Groß/Kleinschreibung zu achten.
Beispiel: s1=“Das Leben ist schoen“, s2 =“schoen“ würde wahr ergeben, s2=“Schoen“ würde falsch ergeben.
Zur Lösung dieser Aufgabe können Sie die Datei suchen.java verwenden.
Aufgabe 4
[Bearbeiten]4. Implementieren Sie eine Methode, die als Eingabe einen beliebigen String s1 akzeptiert und die verschiedenen Zeichen in diesem String zählt (wieder soll auf Groß-/Kleinschreibung geachtet werden. Die Methode soll in der Ausgabe dann alle Zeichen und deren Anzahl ausgeben, die mindestens einmal vorhanden sind. Zeichen, die nicht vorhanden sind, sollen auch nicht ausgegeben werden.
Beispiel: s1=“1Hallo !“, Ausgabe: „1“:1 „H“:1 „a“:1 „l“:2 „o“:1 „!“:1 „ “:1
Zur Lösung dieser Aufgabe können Sie die Datei zaehlen2.java verwenden.
Aufgabe 5
[Bearbeiten]5. Caesar-Chiffre nennt man ein Verschlüsselungsverfahren, das die Buchstaben eines Wortes um eine definierte Anzahl an Zeichen verschiebt.
Beispiel: Wort=“haus“, Verschiebung = 1, chiffriertes Wort: “ibvt“ Implementieren Sie eine Methode, die als Eingabe einen String s1 und eine Zahl i vom Typ integer (aber nur positive) akzeptiert und die Caesar-Chiffre von s1 ausgibt. Vereinfachend dürfen Sie annehmen, dass der String s1 nur aus Kleinbuchstaben von a bis z besteht (kein ö,ä,ü,ß). Zwei Tipps: Der Nachfolgebuchstabe von z ist a und man kann String und Character mit dem + Zeichen addieren. Zum Beispiel ist „Hau“ + ‚s’ = „Haus“.
Zur Lösung dieser Aufgabe können Sie die Datei caesar.java verwenden.
Aufgabe 6
[Bearbeiten]6. Die Fibonacci-Reihe über die natürlichen Zahlen ist wie folgt definiert: f(1)=1 f(2)=1 f(n)=f(n-1) + f(n-2), mit n>2
Zum Beispiel: f(4) = f(3) + f(2) = f(1) + f(1) + f(1) = 1 + 1 + 1 =3
Implementieren Sie eine Methode, die die Fibonacci-Reihe der Integerzahl n ausgibt. Einmal rekursiv und einmal iterativ. Falls Sie nicht wissen, was rekursiv oder iterativ ist, versuchen einfach irgendwie die Fibonacci-Reihe zu implementieren.
Zur Lösung dieser Aufgabe können Sie die Datei fibonacci.java verwenden.
Aufgabe 7
[Bearbeiten]7. Das folgende Verfahren zur Primzahlen-Gewinnung ist als "Sieb des Eratosthenes" bekannt: Streicht man aus der Menge natürlicher Zahlen von 2 bis n, beginnend mit 2, nacheinander alle Vielfachen der jeweils noch verbleibenden Zahlen heraus, enthält die Restmenge nur noch Primzahlen.
Ein Beispiel für die Zahlen 2 bis 15:
-> 2 3 4 5 6 7 8 9 10 11 12 13 14 15
bearbeite 2 -> 2 3 5 7 9 11 13 15
bearbeite 3 -> 2 3 5 7 11 13
bearbeite 5, 7, 11, 13 -> 2 3 5 7 11 13
Implementieren Sie eine Methode, die anhand dieses Verfahrens die Primzahlen unter den ersten 50 bzw. 100 natürlichen Zahlen bestimmt und diese anschließend ausgibt.
Zur Lösung dieser Aufgabe können Sie die Datei eratosthenes.java verwenden.
Aufgabe 8
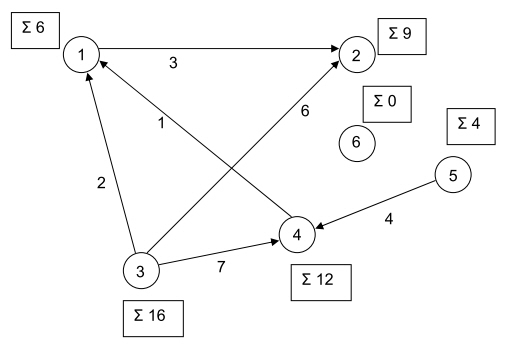
[Bearbeiten]8. Graphen Graphen sind einfach verkettete Listen, die durch gerichtete Kanten miteinander verknüpft sind (s. Skript zur Vorlesung Programmierung). a) Implementieren Sie eine Funktion, mit der Sie überprüfen, ob ein Knoten (in einer Richtung) mit einem anderen Knoten verbunden ist.
Das benötigte Programmgerüst legen Sie bitte als Datei Graph1.java an
public class graph2
{
Knoten knoten;
void summen()
{
//
// ergaenzen Sie bitte hier Ihren Quellcode
//
}
public static void main (String args[])
{
/* Graphen erstellen */
graph2 graph = new graph2();
graph.knoten = new Knoten(1,new Knoten(2,new Knoten(3, new Knoten(4,new Knoten(5,new Knoten(6,null))))));
graph.knoten.kanten = new Kante(graph.knoten.Nf,3,null);
graph.knoten.Nf.Nf.kanten = new Kante(graph.knoten,2,new Kante(graph.knoten.Nf,6,new Kante(graph.knoten.Nf.Nf.Nf,7,null)));
graph.knoten.Nf.Nf.Nf.kanten = new Kante(graph.knoten,1,null);
graph.knoten.Nf.Nf.Nf.Nf.kanten = new Kante(graph.knoten.Nf.Nf.Nf,4,null);
/* summen aufrufen und ausgeben */
graph.summen();
System.out.println("Summen\n======");
System.out.println("Knoten 1: " + graph.knoten.summe + ", richtig ist 6");
System.out.println("Knoten 2: " + graph.knoten.Nf.summe + ", richtig ist 9");
System.out.println("Knoten 3: " + graph.knoten.Nf.Nf.summe + ", richtig ist 15");
System.out.println("Knoten 4: " + graph.knoten.Nf.Nf.Nf.summe + ", richtig ist 12");
System.out.println("Knoten 5: " + graph.knoten.Nf.Nf.Nf.Nf.summe + ", richtig ist 4");
}
}
class Knoten
{
Knoten Nf;
Kante kanten=null;
int summe = 0;
int Nr;
Knoten(int Nummer, Knoten Nachfolger)
{
Nr = Nummer;
Nf = Nachfolger;
}
}
class Kante
{
Kante Nf;
Knoten Ziel;
int gewicht;
Kante(Knoten Zielknoten,int Gewicht, Kante Nachfolger)
{
Ziel = Zielknoten;
Nf = Nachfolger;
gewicht = Gewicht;
}
}