Mathematik/Einführender Text/Platon und Würfelsymmetrie/Vortrag/latex
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Hexahedron.svg} }
\end{center}
\bildtext {... und ein Würfel. Das sind die platonischen Körper.} }
\bildlizenz { Hexahedron.svg } {} {} {Commons} {} {}
-
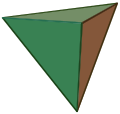
Ein Tetraeder (eine Pyramide mit gleichseitigen Dreiecken als Seiten).
-
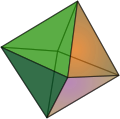
Ein Oktaeder (ein Achtflächner).
-
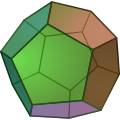
Ein Dodekaeder, der hat zwölf Seiten.
-
Ein Ikosaeder, mit 20 Seiten ...
\seitenueberschrift{Platonische Körper und platonische Liebe - Der Würfel und seine Gruppe}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Platon_altes_Museum2.jpg} }
\end{center}
\bildtext {Plato (427-347 v. C.) sagte: \anfuehrung{die Bedeutung der Geometrie beruht nicht auf ihrem praktischen Nutzen, sondern darauf, daß sie ewige und unwandelbare Gegenstände untersucht und danach strebt, die Seele zur Wahrheit zu erheben}{}.} }
\bildlizenz { Platon_altes_Museum2.jpg } {} {GunnarBach} {Commons} {PD} {}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Fussball.jpg} }
\end{center}
\bildtext {Ein Fußball ist kein regulärer Polyeder. Die Seiten sind Fünfecke und Sechsecke, jedenfalls, wenn man ihn aus Lederstücken zusammennäht. In Wahrheit ist der Ball
\zusatzklammer {als Kugel} {} {} natürlich rund
\zusatzklammer {wie schon Sepp Herberger wußte} {} {,} und überhaupt nicht von ebenen Stücken berandet.} }
\bildlizenz { Fussball.jpg } {} {Indech} {Commons} {CC-by-sa 3.0} {}
Schon dem griechischen Philosophen Platon gefielen solche räumliche Figuren, die durch ebene gleichförmige Seitenstücke begrenzt sind, die selbst wieder regelmäßige Vielecke sind. Man nennt diese Figuren \stichwort {reguläre Polyeder} {} bzw. \stichwort {platonische Körper} {.} Davon gibt es fünf Stück, die alle von Platon in seinem Dialog Timaios beschrieben werden, nämlich den Tetraeder, den Würfel, den Oktaeder, den Dodekaeder und den Ikosaeder. Da Platon ein Philosoph war, kam er auf die etwas merkwürdige Idee, die fünf platonischen Körper mit den Elementen in Beziehung zu setzen, nämlich mit Feuer (Tetraeder), Wasser (Ikosaeder), Luft (Oktaeder), Erde (Würfel); dem Dodekaeder wurde schließlich das Weltall zugeordnet.
\seitenueberschrift{Platons Ideenlehre}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Banquet_cup-bearer_Louvre G467.jpg} }
\end{center}
\bildtext {Bei einem antiken Symposium lag man, trank, lauschte den Flötenspielerinnen und sprach auch über den ...} }
\bildlizenz { Banquet_cup-bearer_Louvre G467.jpg } {} {Jastrow} {Commons} {PD} {}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Simmler-Deotyma.jpg} }
\end{center}
\bildtext {Das Konzept der \anfuehrung{platonischen Liebe}{} wird in Platons Dialog Symposion von der Philosophin Diotima aus Mantinea vorgestellt.} }
\bildlizenz { Simmler-Deotyma.jpg } {Jozef Simmler} {Ejdzej} {Commons} {PD} {}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Oinochoe_Shuvalov_Painter_Louvre_CA1289_n2.jpg} }
\end{center}
\bildtext {... Eros.} }
\bildlizenz { Oinochoe_Shuvalov_Painter_Louvre_CA1289_n2.jpg } {Marie-Lan Nguyen} {Jastrow} {Commons} {CC-by-sa 3.0} {}
Eine bessere Idee von Platon, und zugleich der Grundgedanke seiner Philosophie, war es, dass die sichtbaren Objekte nur unvollkommene Abbilder einer göttlichen Idee sind, die es zu erkennen gilt, um den wesentlichen Kern der Dinge zu erfassen. Dieser Gedanke liegt auch dem Konzept der \stichwort {platonischen Liebe} {} zugrunde, das im Symposion entwickelt wird. Darin wird von einem Gastmahl erzählt, bei dem die Anwesenden, die alle von der Feier am Abend zuvor einen kräftigen Kater haben, übereinkommen, ihr \anfuehrung{Zusammensein nicht auf den Rausch anzulegen, sondern nur so zu trinken zum Vergnügen}{,} und stattdessen der Reihe nach Lobreden auf den Eros vorzutragen, den griechischen Gott der Liebe. Der Höhepunkt dieser Ansprachen bildet die Rede des Sokrates, der sich seinerseits auf Diotima aus Mantinea beruft, mit der er vor vielen Jahren ein Gespräch über dieses Thema hatte. Ihr zur Folge ist Eros gar kein Gott, sondern ein Dämon, ein Vermittler zwischen Gott und den Menschen. Sie schildert mehrere Stufen der Liebe, die auch in einem menschlichen Leben durchlaufen werden können, von \anfuehrung{schönen Gestalten nachzugehen}{} über \anfuehrung{die Schönheit in den Seelen für weit herrlicher [zu] halten als die in den Leibern}{} bis hin zu \anfuehrung{jenes Schöne selbst rein, lauter und unvermischt zu sehen, [...], das göttliche Schöne selbst in seiner Einartigkeit zu schauen}{.} Ziel ist es somit nicht, Abbilder des Guten und Schönen zu berühren, sondern das Wahre selbst, um so Glückseligkeit und damit Anteil an der Unsterblichkeit zu erlangen.
Der Gedanke, dass sichtbare Dinge den Anstoß geben sollen, nach tiefer liegenden Wahrheiten zu suchen, von denen diese Dinge nur ein schwaches Abbild sind und durch die sie erst richtig verstanden werden können, ist auch für die \zusatzklammer {reine} {} {} Mathematik von zentraler Bedeutung. Mathematisches Denken ist seiner Natur nach abstraktes Denken, das, manchmal ausgehend von konkreten Objekten, nach Strukturen, Gesetzmäßigkeiten, allgemeingültigen Regeln sucht. Es geht dadrum, mathematische Theorien zu entwicklen, um die gemeinsame Struktur verwandter Objekte zu verstehen.
Was ist also die zugrunde liegende Idee hinter den platonischen Körpern, wie sieht ihre innere Struktur aus, zu welcher mathematischen Theorie geben sie Anlass? Wir beschränken uns auf den Würfel.
\seitenueberschrift{Symmetrien}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Snijden_kruisen_evenwijdig.png} }
\end{center}
\bildtext {} }
\bildlizenz { Snijden_kruisen_evenwijdig.png } {} {MADe} {nl.wikipedia} {cc-by-sa 3.0} {}
Bei den platonischen Körpern fällt natürlich ihre große Regelmäßigkeit auf, die ihre Schönheit und Anziehungskraft ausmachen. Die Regelmäßigkeit beinhaltet, dass in einem platonischen Körper jede Seite in jede andere Seite, jede Kante in jede andere Kante und jeder Eckpunkt in jeden Eckpunkt überführt werden kann. D.h., dass diese Körper eine reichhaltige Symmetrie aufweisen. In der Mathematik ist es gerade die Menge der Symmetrien, und ihre Beziehungen untereinander, für die man sich interessiert. Die körperlichen Objekte sind sozusagen der Anlass für die Theorie. Wenn man die Theorie entwickelt hat, so kann man die konkreten Objekte als eine konkrete Realisierung der Theorie verstehen.
Unter einer \stichwort {(eigentlichen) Symmetrie} {} eines Körpers $K$ (im Raum) versteht man eine wirklich durchführbare \stichwort {Bewegung} {,} die den Körper in sich überführt, und bei der die innere Struktur des Körpers nicht verändert wird.
Bei einer solchen Bewegung wird der Körper als ein starres Ganzes genommen, irgendwie gedreht und verschoben, aber weder zerrissen noch deformiert. Die Endlage des Körpers soll deckungsgleich mit der Ausgangslage sein. Wir interessieren uns bei einer solchen Bewegung lediglich für das Verhältnis von Ausgangslage zu Endlage, nicht für die Zwischenschritte und den realen Bewegungsvorgang. Ein Bewegung ist also dadurch festgelegt, dass für jeden Punkt des Körpers die neue Lage des Punktes bekannt ist. Insofern ist eine Symmetrie einfach eine \definitionsverweis {Abbildung}{}{} \maabbdisp {\varphi} {K} {K } {} mit gewissen zusätzlichen Eigenschaften.
Dass die Bewegung wirklich durchführbar sein soll schließt beispielsweise Spiegelungen an einer Ebene aus (sowas nennt man auch eine uneigentliche Bewegung).
Dass die innere Struktur nicht verändert wird, kann man so ausdrücken, dass sich bei der Bewegung zu je zwei Punkten der Abstand nicht ändert, dass also für alle
\mathl{P,Q\in K}{} die Abstandsbeziehung
\mathdisp {d(\varphi(P),\varphi(Q))=d(P,Q)} { }
gilt. Man spricht auch von einer \stichwort {Isometrie} {.}
\seitenueberschrift{Welche Symmetrien hat ein Würfel?}
Schauen wir uns einen Würfel an. Eine \stichwort {Würfelsymmetrie} {} führt den Würfel durch eine Bewegung in sich selbst über. Bei einer solchen Bewegung verändert der Würfelmittelpunkt seine Lage nicht, und es werden, aufgrund des \stichwort {Starrheitsprinzips} {,} Seiten auf Seiten, Kanten auf Kanten und Ecken auf Ecken abgebildet. Ebenso werden Seitenmittelpunkte auf Seitenmittelpunkte abgebildet, und gegenüberliegende Seitenmittelpunkte werden auf gegenüberliegende Seitenmittelpunkte abgebildet. Ferner werden Kantenmittelpunkte auf Kantenmittelpunkte abgebildet, Seitendiagonale auf Seitendiagonale, Raumdiagonale auf Raumdiagonale.
Notieren wir einfach mal eine Liste von Würfelsymmetrien, wie sie uns in den Sinn kommen.
\zwischenueberschrift{Drehungen um eine Seitenmittelpunktsachse}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Würfel.Tafel.Symmetrieserie.4.JPG} }
\end{center}
\bildtext {Eine Vierteldrehung um die vertikale Achse. Betont wird die Wirkungsweise auf den Eckpunkten.} }
\bildlizenz { Würfel.Tafel.Symmetrieserie.4.JPG } {Brenner} {} {Commons} {CC-by-sa 3.0} {}
Man kann beispielsweise durch den oberen Seitenmittelpunkt und den unteren Seitenmittelpunkt sich eine Achse $\alpha$ denken, und um diese Achse den Würfel drehen. Damit der Würfel mit seiner Ausgangslage zur Deckung gebracht wird, muss der Drehwinkel ein Vielfaches von neunzig Grad sein, also eine Vierteldrehung, eine Halbdrehung, eine Dreivierteldrehung oder eine Volldrehung. Bei einer Volldrehung, also einer Drehung um diese Achse um 360 Grad, wird jeder Punkt auf sich selbst abgebildet. Man könnte den Würfel genauso gut auch gar nicht drehen. Man spricht von der \stichwort {identischen Drehung} {,} der \stichwort {Identität} {} oder der \stichwort {trivialen Symmetrie} {.} Wie die $0$ eine enorm wichtige Zahl ist, obwohl die Addition mit ihr \anfuehrung{nichts}{} macht, so ist auch diese triviale Symmetrie enorm wichtig für die Theorie der (Würfel-)Symmetrien.
\zwischenueberschrift{Drehungen um eine Kantenmittelpunktsachse}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Würfel.Tafel.Symmetrieserie.6.JPG} }
\end{center}
\bildtext {Eine Halbdrehung um eine Kantenmittelpunktsachse. Betont wird die Wirkungsweise auf den Eckpunkten.} }
\bildlizenz { Würfel.Tafel.Symmetrieserie.6.JPG } {Brenner} {} {Commons} {CC-by-sa 3.0} {}
Zu jeder der zwölf Würfelkanten gibt es einen \stichwort {Kantenmittelpunkt} {.} Ein solcher Kantenmittelpunkt definiert mit dem Mittelpunkt der gegenüber liegenden Kante eine Kantenmittelpunktsachse. Betrachten wir beispielsweise die Kantenmittelpunktsachse $\beta$, die durch die Mittelpunkte der durch
\mathkor {} {A} {und} {E} {}
und durch
\mathkor {} {C} {und} {G} {}
gegebenen Kanten definiert ist. Gibt es um diese Achse eine Drehung
\zusatzklammer {abgesehen von der Identität} {} {,} die den Würfel in sich überführt? Wir haben gesagt, dass bei einer Würfelsymmetrie Eckpunkte auf Eckpunkte abgebildet werden. Die Kante von $A$ nach $E$ steht senkrecht auf der Drehachse, daher kommen als Bildpunkte von $A$ nur $A$ selbst oder $E$ in Frage. Im ersten Fall liegt die Identität vor, im zweiten Fall eine Halbdrehung um die angegebene Achse, die in der Tat den Würfel in sich überführt. Bei dieser Halbdrehung werden
\mathkor {} {A} {und} {E} {,}
\mathkor {} {C} {und} {G} {,}
\mathkor {} {D} {und} {F} {}
und schließlich
\mathkor {} {B} {und} {H} {}
vertauscht.
\zwischenueberschrift{Drehungen um eine Raumdiagonale}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Würfel.Tafel.Symmetrieserie.8.JPG} }
\end{center}
\bildtext {Eine Dritteldrehung um eine Raumdiagonale. Betont wird die Wirkungsweise auf den Eckpunkten.} }
\bildlizenz { Würfel.Tafel.Symmetrieserie.8.JPG } {Brenner} {} {Commons} {CC-by-sa 3.0} {}
Jeder der acht Eckpunkte des Würfels definiert zusammen mit dem gegenüber liegenden Eckpunkt eine \stichwort {Raumdiagonale} {}
\zusatzklammer {oder eine \stichwort {Eckpunktsachse} {}} {} {.} Betrachten wir beispielsweise die durch die Eckpunkte
\mathkor {} {E} {und} {C} {}
gegebene Raumdiagonale $\gamma$. Gibt es Drehungen um diese Achse, die den Würfel in sich überführen? Das können wir uns wieder anhand der Eckpunkte klar machen. Die Punkte
\mathkor {} {E} {und} {C} {}
liegen auf der Drehachse und verändern daher nicht ihre Position. Wohin kann beispielsweise der Punkt $A$ durch eine solche Drehung abgebildet werden? $A$ ist ein zu $E$ \anfuehrung{benachbarter}{} Eckpunkt
\zusatzklammer {d.h.,
\mathkor {} {A} {und} {E} {} sind durch eine Kante direkt verbunden} {} {,}
und diese Eigenschaft bleibt bei einer Symmetrie erhalten. Die möglichen Bildpunkte müssen also ebenfalls zu $E$ benachbart sein, und das sind genau die Punkte
\mathkor {} {A,H} {und} {F} {}
\zusatzklammer {Drehen Sie einen Würfel so hin, dass Sie einen Eckpunkt in der Mitte des Gesichtsfelds haben. Sie sehen dann drei Seiten und drei benachbarte Eckpunkte und drei nicht benachbarte Eckpunkte. Nur den gegenüber liegenden Eckpunkt sehen Sie nicht} {} {.}
In der Tat gibt es drei Drehungen um eine Raumdiagonale, die den Würfel in sich überführen, nämlich die Drehung um $0$ Grad
\zusatzklammer {also wieder die Identität} {} {,} die Drehung um $120$ Grad und die Drehung um $240$ Grad.
Die Identität kann dabei als eine Achsendrehung um jede der drei Achsentypen um den Winkel $0$ aufgefasst werden. Gibt es außer den genannten Drehungen noch weitere eigentliche Würfelsymmetrien? Wie kann man sich sicher sein, dass man alle Symmetrien gefunden hat?
\seitenueberschrift{Verknüpfung von Symmetrien}
Wir haben nun eine Liste von einzelnen Würfelsymmetrien angeführt, doch wie verhalten sie sich zueinander, gibt es eine umfassende Struktur, in der all diese Symmetrien ihren Platz finden? Unser Ausgangspunkt ist, dass man zwei Bewegungen
\zusatzklammer {Abbildungen} {} {} \mathkon { \varphi } { und } { \psi }{ } \stichwort {verknüpfen} {} kann, indem man sie \stichwort {hintereinander ausführt} {,} also zuerst die erste Würfelsymmetrie und dann die zweite Würfelsymmetrie anwendet. Diese \stichwort {Verkettung} {} erfüllt wieder alle Bedingungen, die wir an eine Symmetrie gestellt haben. Des weiteren gibt es zu einer Bewegung die \stichwort {entgegengesetzte Bewegung} {,} bei der die Bewegung rückläufig durchgeführt wird. Bei einer physikalischen Realisierung der Bewegung würde man einfach die Zeitrichtung umdrehen.
Insgesamt erhalten wir, dass die Menge aller Symmetrien an einem Körper folgende drei strukturelle Eigenschaften aufweist.
\aufzaehlungdrei{Bewegungen lassen sich hintereinander ausführen, d.h. wenn man zwei Bewegungen \mathkon { \varphi } { und } { \psi }{ } hat, so ist auch die \stichwort {Hintereinanderausführung} {}
\mathl{\psi \circ \varphi}{,} die zuerst $\varphi$ und dann $\psi$ durchführt, sinnvoll definiert und wieder eine Bewegung.
}{Die \stichwort {identische Bewegung} {,} die nichts bewegt, ist eine Bewegung. Wenn man zu einer beliebigen Bewegung die identische Bewegung davor oder danach durchführt, so ändert das die Bewegung nicht.
}{Zu einer Bewegung $\varphi$ gibt es die \stichwort {entgegengesetzte Bewegung} {} \zusatzklammer {oder \anfuehrung{Rückwärtsbewegung}{}} {} {} $\varphi^{-1}$, die die Eigenschaft besitzt, dass die Hintereinanderausführungen \mathkon { \varphi^{-1} \circ \varphi } { und } { \varphi \circ \varphi^{-1} }{ } einfach die Identität sind.
}
Für eine Menge
\zusatzklammer {also beispielsweise die Menge der Bewegungen an einem Körper, nicht der Körper als Menge!} {} {,} auf der es eine Verknüpfung mit diesen drei Eigenschaften gibt, gibt es innerhalb der Mathematik einen eigenen Namen: man spricht von einer \stichwort {Gruppe} {,} ihre Definition sieht folgendermaßen aus.
\inputdefinition
{
}
{
Eine Menge $G$ mit einem ausgezeichneten Element
\mavergleichskette
{\vergleichskette
{e
}
{ \in }{G
}
{ }{
}
{ }{
}
{ }{
}
}
{}{}{}
und mit einer
\definitionsverweis {Verknüpfung}{}{}
\maabbeledisp {} {G \times G} {G
} {(g,h)} { g \circ h
} {,}
heißt
\definitionswort {Gruppe}{,}
wenn folgende Eigenschaften erfüllt sind.
\aufzaehlungdrei{Die Verknüpfung ist \stichwort {assoziativ} {,} d.h. für alle
\mavergleichskette
{\vergleichskette
{ f,g,h
}
{ \in }{G
}
{ }{
}
{ }{
}
{ }{
}
}
{}{}{}
gilt
\mavergleichskettedisp
{\vergleichskette
{ (f \circ g) \circ h
}
{ =} { f \circ (g \circ h)
}
{ } {
}
{ } {
}
{ } {
}
}
{}{}{.}
}{Das Element $e$ ist ein \stichwort {neutrales Element} {,} d.h. für alle
\mavergleichskette
{\vergleichskette
{g
}
{ \in }{G
}
{ }{
}
{ }{
}
{ }{
}
}
{}{}{}
gilt
\mavergleichskettedisp
{\vergleichskette
{ g \circ e
}
{ =} { g
}
{ =} { e \circ g
}
{ } {
}
{ } {
}
}
{}{}{.}
}{Zu jedem
\mavergleichskette
{\vergleichskette
{g
}
{ \in }{G
}
{ }{
}
{ }{
}
{ }{
}
}
{}{}{}
gibt es ein \stichwort {inverses Element} {,} d.h. es gibt ein
\mavergleichskette
{\vergleichskette
{h
}
{ \in }{G
}
{ }{
}
{ }{
}
{ }{
}
}
{}{}{}
mit
\mavergleichskettedisp
{\vergleichskette
{ h \circ g
}
{ =} { g \circ h
}
{ =} { e
}
{ } {
}
{ } {
}
}
{}{}{.}
}
}
Wie sieht die Gruppe aller Würfelsymmetrien aus? Ist unsere obige Liste aus der Identität und den verschiedenen beschriebenen Achsendrehungen schon diese ganze Gruppe? Schauen wir uns ein Beispiel an, wo zwei solche Drehungen miteinander verknüpft werden.
\inputbeispiel{}
{
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Würfel.Tafel.Symmetrieserie.9.JPG} }
\end{center}
\bildtext {Die beiden Drehachsen.} }
\bildlizenz { Würfel.Tafel.Symmetrieserie.9.JPG } {Brenner} {} {Commons} {C-by-sa 3.0} {}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Würfel.Tafel.Symmetrieserie.10.JPG} }
\end{center}
\bildtext {Die Wirkung der beiden Drehungen auf einigen Punkten.} }
\bildlizenz { Würfel.Tafel.Symmetrieserie.10.JPG } {Brenner} {} {Commons} {C-by-sa 3.0} {}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Würfel.Tafel.Symmetrieserie.11.JPG} }
\end{center}
\bildtext {Die Wirkung der beiden Drehungen auf allen Eckpunkten.} }
\bildlizenz { Würfel.Tafel.Symmetrieserie.11.JPG } {Brenner} {} {Commons} {C-by-sa 3.0} {}
Es sei $\alpha$ die Achse durch die Seitenmittelpunkte der oberen und der unteren Seite, und es sei $\varphi$ die Drehung um diese Achse um $90$ Grad gegen den Uhrzeigersinn von oben betrachtet. Es sei $\delta$ die Achse durch die Seitenmittelpunkte der vorderen und der hinteren Seite, und es sei $\psi$ die Drehung um diese Achse um $90$ Grad mit dem Uhrzeigersinn von vorne betrachtet. Was kann man über die Verknüpfung sagen, bei der zuerst $\varphi$ und dann $\psi$ durchgeführt wird? In einer solchen Situation ist es hilfreich, die Bewegungen dadurch zu verstehen, dass man ihre \stichwort {Wirkungsweise} {} auf charakteristischen Punkten des Würfels, beispielsweise auf seinen Eckpunkten, untersucht.
Die erste Drehung hat auf den Eckpunkten folgende Wirkung,
\wertetabelleachtausteilzeilen { Punkt }
{\mazeileundfuenf {A} {B} {C} {D} {E} }
{\mazeileunddrei {F} {G} {H
} }
{ Bildpunkt }
{\mazeileundfuenf {D} {A} {B} {C} {H} }
{\mazeileunddrei {E} {F} {G
} }
Die zweite Drehung hat die folgende Wirkung,
\wertetabelleachtausteilzeilen { Punkt }
{\mazeileundfuenf {A} {B} {C} {D} {E} }
{\mazeileunddrei {F} {G} {H
} }
{ Bildpunkt }
{\mazeileundfuenf {D} {C} {G} {H} {A} }
{\mazeileunddrei {B} {F} {E
} }
Die Wirkungsweise der zusammengesetzten Bewegung auf den Eckpunkten ergibt sich einfach dadurch, dass man schaut, wohin das Ergebnis der ersten Bewegung unter der zweiten Bewegung geschickt wird. In unserem Beispiel ergibt sich
\wertetabelleachtausteilzeilen { Punkt }
{\mazeileundfuenf {A} {B} {C} {D} {E} }
{\mazeileunddrei {F} {G} {H
} }
{ Bildpunkt }
{\mazeileundfuenf {H} {D} {C} {G} {E} }
{\mazeileunddrei {A} {B} {F
} }
Es fällt dabei auf, dass unter der Verknüpfung die beiden Punkte
\mathkor {} {C} {und} {E} {}
auf sich selbst abgebildet werden. Damit wird auch die Raumdiagonale durch diese beiden Punkte bei dieser Bewegung nicht verändert, und es liegt in der Tat eine Drehung um diese Raumdiagonale als Drehachse vor. Da $A$ auf $H$ abgebildet wird, handelt es sich um die Drehung um $120$ Grad im Uhrzeigersinn, wenn man auf diese Achse von vorne links unten schaut.
}
In diesem Beispiel führte also die Verkettung von zwei Symmetrien wieder zu einer Symmetrie, und zwar zu einer Symmetrie, die schon in unserer Liste steht. Wir wissen noch nicht, ob unsere Liste in dem Sinne vollständig ist, dass mit je zwei Symmetrien auch deren Verknüpfung wieder zu dieser Liste gehört. Das könnten wir mit einigem Aufwand überprüfen, indem wir alle Kombinationen durchspielten. Wir werden aber einen einfacheren Weg gehen.
\seitenueberschrift{Wie viele Symmetrien hat ein Würfel?}
Wie viele eigentliche Würfelsymmetrien gibt es? Um diese Frage beantworten zu können, ist es wieder hilfreich, die Wirkung der Symmetrien auf der Menge der Eckpunkte zu betrachten. Offenbar kann man den Punkt $A$ auf jeden anderen Eckpunkt, nennen wir ihn $X$, bewegen. Dazu genügt es beispielsweise, einige Vierteldrehungen um verschiedene Seitenmittelpunktsachsen hintereinander durchzuführen. Es gibt dabei allerdings mehrere Bewegungen, die $A$ auf $X$ abbilden. Was kann beispielsweise mit $B$ unter einer solchen Bewegung geschehen? Da $B$ zu $A$ benachbart ist, muss auch der Bildpunkt von $B$ zum Bildpunkt von $A$, also zu $X$, benachbart sein. Dafür gibt es genau drei Möglichkeiten, da $X$ eben genau zu drei Eckpunkten benachbart ist. Durch eine Drehung um die Raumdiagonale durch $X$ kann auch jede dieser Möglichkeiten verwirklicht werden. Es gibt also
\mathl{8 \cdot 3 = 24}{} verschiedene Möglichkeiten, für die beiden Eckpunkte
\mathkor {} {A} {und} {B} {} die Bildpunkte auszuwählen. Wenn für diese beiden Punkte die
\zusatzklammer {benachbarten} {} {}
Bildpunkte
\mathkor {} {X} {und} {Y} {}
ausgewählt sind, gibt es dann immer noch verschiedene Möglichkeiten, eine solche Bewegung zu realisieren? Wir behaupten, dass es dann genau nur eine Möglichkeit gibt, dass also diese Auswahl die Symmetrie eindeutig festlegt. Wir müssen also zeigen, dass wenn
\mathkor {} {\varphi_1} {und} {\varphi_2} {}
zwei Würfelsymmetrien sind, die
\mathdisp {\varphi_1(A) = \varphi_2(A)=X \text{ und } \varphi_1(B) = \varphi_2(B)=Y} { }
erfüllen, dass dann überhaupt
\mathl{\varphi_1= \varphi_2}{} ist. Um dies einzusehen, verwenden wir einen typischen Schluss der Gruppentheorie, der schon die Schlagkraft dieses Konzepts deutlich macht. Wir betrachten die Verknüpfung von $\varphi_1$ mit der entgegengesetzten Bewegung zu $\varphi_2$, also
\mathdisp {\psi = \varphi_2^{-1} \circ \varphi_1} { . }
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Würfel.Tafel.Symmetrieserie.12.JPG} }
\end{center}
\bildtext {Wenn eine Symmetrie
\mathkor {} {A} {und} {B} {} nicht bewegt, so wird auch die Kante dazwischen nicht bewegt.} }
\bildlizenz { Würfel.Tafel.Symmetrieserie.12.JPG } {Brenner} {} {Commons} {CC-by-sa 3.0} {}
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Wuerfelstarr.6.JPG} }
\end{center}
\bildtext {Dann wird auch die ganze Ebene durch diese Kante und den Würfelmittelpunkt nicht bewegt.} }
\bildlizenz { Wuerfelstarr.6.JPG } {Brenner} {} {Commons} {CC-by-sa 3.0} {}
Unter dieser Bewegung $\psi$ geht zunächst $A$ auf $X$ und dann $X$ wiederum auf $A$, ebenso geht insgesamt $B$ auf $B$. Damit ist $\psi$ eine Bewegung, die die gesamte Kante zwischen
\mathkor {} {A} {und} {B} {}
unverändert lässt. Da bei einer Würfelsymmetrie der Würfelmittelpunkt $M$ unverändert bleibt, bleibt wegen der Starrheit auch das gesamte Dreieck zu den Punkten
\mathl{A,B,M}{} unverändert und damit auch die gesamte Ebene, in der dieses Dreieck liegt. Die Starrheit erzwingt weiter, dass dann bereits der gesamte Würfel unter $\psi$ unverändert bleibt
\zusatzklammer {die Spiegelung an dieser Ebene ist eine uneigentliche Symmetrie, die nicht durch eine Bewegung realisiert werden kann} {} {,} dass also
\mathdisp {\psi = \varphi_2^{-1} \circ \varphi_1 = \operatorname{Id} \,} { }
die Identität ist. Durch Anwenden von $\varphi_2$ von links auf diese Gleichung ergibt sich daraus
\mathdisp {\varphi_1 = \varphi_2} { . }
Damit haben wir den folgenden Satz bewiesen.
\inputfakt{Würfel/Eigentliche Symmetrien/24/Fakt}{Satz}{}
{
\faktsituation {}
\faktfolgerung {Der Würfel besitzt $24$
\definitionsverweis {eigentliche Symmetrien}{}{.}}
\faktzusatz {}
\faktzusatz {}
}
\seitenueberschrift{Alle Würfelsymmetrien sind Achsendrehungen}
Abschließend zeigen wir, dass unsere eingangs aufgestellte Liste von Würfelsymmetrien vollständig ist. Wir wissen nun, dass es überhaupt nur $24$ Würfelsymmetrien gibt. Gehen wir also unsere Liste durch und schauen, wie viele Symmetrien wir dort schon erfasst haben.
\aufzaehlungvier{Es gibt die Identität.
}{Es gibt sechs Seiten und drei Seitenmittelpunktsachsen, wobei man jeweils um die drei Winkel
\mathl{90,180,270}{} Grad drehen kann
\zusatzklammer {die Drehung um $0$ Grad darf man nicht mitzählen, da dies die Identität ist} {} {.} Davon gibt es neun Stück.
}{Es gibt zwölf Kanten und daher sechs Kantenmittelpunktsachsen. Um diese Achsen gibt es jeweils eine Halbdrehung, macht sechs Stück.
}{Es gibt acht Eckpunkte und daher vier Raumdiagonalen. Um diese Achsen gibt es jeweils die Dritteldrehung und die Zweidritteldrehung, macht acht Stück.
}
Wir müssen noch sicherstellen, dass wir dabei keine Bewegung doppelt gezählt haben. Wenn aber eine Bewegung zweimal auftaucht, so hat sie mindestens zwei verschiedene Drehachsen. Diese Drehachsen bleiben bei der Bewegung unverändert, daher bleibt die ganze von diesen Achsen erzeugte Ebene unverändert, und damit sogar der ganze Raum und es liegt die Identität vor. Wegen
\mathdisp {1+9+6+8=24} { }
folgt der nächste Satz.
\inputfakt{Würfel/Eigentliche Symmetrien/Achsendrehung/Fakt}{Satz}{}
{
\faktsituation {}
\faktfolgerung {Jede eigentliche Würfelsymmetrie ist
\zusatzklammer {die Identität oder} {} {} eine Achsendrehung um eine Seitenmittelpunktsachse, um eine Kantenmittelpunktsachse oder um eine Raumdiagonale.}
\faktzusatz {}
\faktzusatz {}
}
\seitenueberschrift{Alle Fußballspiele sind Achsendrehungen}
Dieser letzte Satz besitzt eine weitgehende Verallgemeinerung, nämlich, dass jede lineare eigentliche Isometrie im Raum eine Drehung um eine Achse ist. Aus Anlass der Fußballweltmeisterschaft erwähnen wir folgende Version dieses Satzes. Denken Sie beim nächsten langweiligen Spiel daran.
\bild{ \begin{center}
\includegraphics[width=5.5cm]{\bildeinlesung {Anstoß_im_Finale_Confed-Cup_2005.JPG} }
\end{center}
\bildtext {} }
\bildlizenz { Anstoß_im_Finale_Confed-Cup_2005.JPG } {} {Florian K} {Commons} {CC-by-sa 3.0} {}
\inputfakt{Lineare Isometrie/Raum/Fixpunkte auf Fußball/Fakt}{Satz}{Satz vom Fußball}
{
\faktsituation {Zu Beginn eines Fußballspiels liegt der Fußball auf dem Anstoßpunkt. Wenn ein Tor erzielt wird, so wird der Ball wieder auf den Anstoßpunkt zurückgesetzt.}
\faktuebergang {In dieser Situation gilt:}
\faktfolgerung {Es gibt mindestens zwei
\zusatzklammer {gegenüber liegende} {} {} Punkte auf dem Fußball
\zusatzklammer {seiner Oberfläche} {} {,} die beim Neuanstoß genau dort liegen, wo sie am Spielanstoß lagen. Die Gesamtbewegung des Balles lässt sich durch eine Achsendrehung realisieren.}
\faktzusatz {}
\faktzusatz {}
}