Mechanische ebene Kurven/Stangenkoppelung/Zwei Kreise/Beispiel

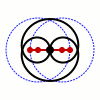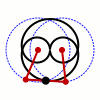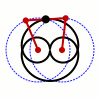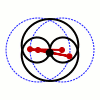
Als Bahnen betrachten wir jetzt zwei Kreise, wobei wir uns auf gleichen Radius beschränken, den wir zu ${}1$ normieren. Durch verschieben können wir annehmen, dass ${}(0,0)$ und ${}(0,a)$ die Mittelpunkte der beiden Kreise sind. Die Länge der Koppelungsstange sei wieder ${}d$, sodass die drei algebraischen Gleichungen

1. ${}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}=d^{2}$
2. ${}x_{1}^{2}+y_{1}^{2}=1$
3. ${}(x_{2}-a)^{2}+y_{2}^{2}=1$

das mechanische System beschreiben. Wir interessieren uns für die Trajektorie des Mittelpunktes der Stange. Dessen Koordinaten sind gegeben durch

${}z_{1}={\frac {1}{2}}x_{1}+{\frac {1}{2}}y_{1}{\text{ und }}z_{2}={\frac {1}{2}}x_{2}+{\frac {1}{2}}y_{2}\,.$

Wir drücken das System in den Variablen ${}z_{1},z_{2},x_{1},x_{2}$ aus, ersetzen ${}y_{1}=2z_{1}-x_{1},y_{2}=2z_{2}-x_{2}$ und erhalten

1. ${}(x_{2}-x_{1})^{2}+(2z_{2}-2z_{1}-x_{2}+x_{1})^{2}=d^{2}$
2. ${}x_{1}^{2}+(2z_{1}-x_{1})^{2}=2x_{1}^{2}+4z_{1}^{2}-4x_{1}z_{1}=1$
3. ${}(x_{2}-a)^{2}+(2z_{2}-x_{2})^{2}=4z_{2}^{2}-4x_{2}z_{2}+x^{2}+(x_{2}-a)^{2}=1$ .

In der Gleichung (3) kommt ${}x_{1}$ nicht vor, und aus den Gleichungen (1) und (2) wollen wir ${}x_{1}$ eliminieren.