Populationsdynamik: Gewichtung von Lehrern und Schülern in der Region PACA

(A1) Modellierungsthema

Dadurch, dass seit 2015 immer mehr Menschen nach Südfrankreich einwandern, stellt sich die Frage ob es in der nahen Zukunft noch genügend Lehrkräfte für die zusätzliche Anzahl an Schülern geben wird. Es wird speziell auf Zahlen der Region [1] "Provence-Alpes-Côte d'Azur", kurz: PACA zurückgegriffen.

Diverse Faktoren/Daten müssen dabei beachtet/eingeholt werden:

• Geburtenrate
• Sterberate
• Zuwanderungsrate
• Auswanderungsrate
• Lehramtsstudierende
• Lehrer

Ziel

• Wie viele Einwohner hat die Region PACA in 50 Jahren ?
• Wie viele Schüler hat diese Region?
• Wie viele Lehrer hat diese Region?
• Die Frage "gibt es genügend Lehrer im Schuljahr 2068/2069?" soll beantwortet werden.
• Lösung des Problems: Verbesserung der Lehrerausbildung

Modellierungszyklen

Erster Modellierungszyklus

Vorbereitung:

Für den ersten Modellierungszyklus werden die verschiedenen Faktoren einer Änderung der Einwohnerzahlen für die letzten sieben Jahre und folgenden 50 Jahre (bis zum Jahr 2068) recherchiert und berechnet. Hierbei werden die Veränderungen der Einwohnerzahl, Geburten-, Sterbe-, Auswanderungs- und Zuwachsrate beachtet. Aus Statistiken sollen die Einwohnerzahlen berechnet werden und vor allem wie viele SchülerInnen es geben wird.

• Recherche der Einwohnerzahlen in der Vergangenheit
• Statistiken
• Erste Berechnungen der Einwohnerzahl für die Zukunft
• Diagramme erstellen
• Programm: Tabellenkalkulation (Exel)

Erste eingeholte und errechnete Daten:

• Einwohnerzahl der Region PACA von 1990-2018

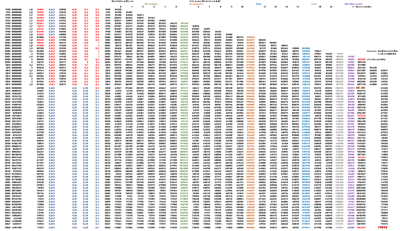
Anhand diverser offizieller Statistiken haben wir die Einwohnerzahlen der Jahre 1990 bis 2018 abgelesen. Ebenfalls aus Statistiken haben wir alle in folgender Graphik schwarzen Zahlen abgelesen. Die roten Zahlen wurden errechnet und die blauen geschätzt.

Die Geburtenrate wurde errechnet, indem die Anzahl der Geburten aus dem jeweiligen Jahr durch die Anzahl der Gesamteinwohner geteilt wurden. Das Ergebnis wurde auf drei Nachkommastellen gerundet. Durch die Rundung kam bei jedem Jahr in dem die Anzahl der Geburten und Einwohner bekannt war, die gleiche Geburtenrate (0,012) heraus. Daher haben wir die Geburtenrate auch auf die Jahre übertragen in denen die Anzahl der Geburten nicht bekannt waren. Die fehlende Anzahl an Geburten wurde nun anhand der geschätzten Geburtenrate errechnet
(Einwohneranzahl * 0,012 = Anzahl Geburten)

Die Sterberate ergab gerundet auch jedes Jahr die gleiche (0,1 = Runden(Anzahl Tode : Gesamteinwohnerzahl)).

Die Zuwachsrate wurde ebenfalls als gerundeter Wert ausgerechnet indem man folgendes bei Excel eingab:

=Runden(((Einwohnerzahl Jahr x /Einwohnerzahl Jahr x - 1 ) - 1) * 100; 1) Anhand der Zuwachsrate konnte man nun die Einwanderungsrate bestimmen:

=RUNDEN((((Einwohnerzahl Jahr x / Einwohnerzahl Jahr x - 1 ) - Geburtenrate + Sterberate ) - 1 ) * 100; 1)

• Einwanderungsalter

Nun wurde die Anzahl an Einwandererkindern pro Jahrgang ausgerechnet

• wir gehen davon aus, dass egal bei welchem Alter gleich viel Prozent an Einwanderern dazu kommen, daher sind die Anzahl an 3-16 Jährigen 14/18 der Gesamtzahl (0-17 Jahre), und jedes einzelne Alter zwischen 0 und 17 Jahren 1/18 der Gesamtzahl.

• des Weiteren wird angenommen, dass die Einwanderungsrate dauerhaft gleich bleibt bei 0,25 % (Schnitt der Einwanderungsrate der letzten 4 Jahre)

Daraus folgt, dass jedes Alter zwischen 0 und 17 Jahren 2,2%*0,25% = 0,0055% der Gesamteinwohnerzahl ausmachen.

• Anzahl schulpflichtiger Kinder

Um die Anzahl der schulpflichtigen Kinder in 50 Jahren heraus zu finden wurde viel geplottet. Da das Bild der Tabelle zu unübersichtlich ist, werden im Folgenden nochmal Teilausschnitte größer gezeigt und Vorgänge erläutert.

Um die schulpflichtigen Kinder zu errechnen, wurde im Jahr 1990 zuerst die Anzahl der 0 Jährigen errechnet.

= (Runden (Geburtenanzahl + ( Gesamteinwohnerzahl * 0,000055 )) ; 0)

Gesamteinwohnerzahl * 0,000055 entspricht den 0-Jährigen Einwandererkindern.

Die Funktion wurde bis zum Jahr 2068 geplottet. Um die einjährigen Kinder im nächsten Jahr zu errechnen wurde der Wert der 0 - Jährigen 1990er Kinder mit der Säuglingssterblichkeit von 0,33 multipliziert. So geht es auch für die älteren Kinder weiter, nur ändert sich die Säuglingssterblichkeit in Kindersterblichkeit und wird je älter die Kinder sind immer kleiner (s. Tabelle 1. Zeile).

Um die Gesamteinwohnerzahlen und die Anzahl der Geburten in der Zukunft zu generieren, wurde die Durchschnittszuwachsrate der letzten 8 Jahre berechnet und mit dieser weitergerechnet. Die Geburtenrate zu den letzten Jahren ist auch gleich geblieben, womit man dann die Geburten berechnen konnte. Bis 2018 beruhen alle Einwohnerzahlen auf Rohdaten, ein Teil der Geburtenanzahl war auch gegeben, andere und die Zukunftsdaten sind simulierte Zahlen die nicht der Wahrheit entsprechen müssen.

Laut der Berechnungen wird es also im Jahr 2068 1062122 Schülerinnen und Schüler geben. Da 75 Lehrer auf 1000 Schüler benötigt werden brauchen wir im Jahr 2068 in der Region PACA 79659 Lehrkräfte. (Berechnung: =Runden (( schulpflichtige Kinder * 75 / 1000); 0 )

• Anzahl Studenten

Hinführung

In Frankreich wird sich immer für ein Jahr beworben, sodass es nur Daten für das ganze Jahr gibt und nicht für die einzelnen Semester so wie es bei uns bekannt ist. Unter der Gesamtzahl der Studierenden in der Region PACA bewerben sich 25% für das Lehramtsstudium. Basierend auf den recherchierten Daten und der Anzahl der Gesamtstudenten in der Region können die fehlenden Daten der Lehramtsstudenten ermittelt werden. Die Stundentenzahlen werden für die Lehreranzahl im Jahr 2068 gebraucht.

Durchführung

Anhand der errechneten Lehramtsstudentenzahlen wird nun die Lagrange-Interpolation angewendet.

Interpolationsverfahren

Unter Polynominterpolation versteht man die Suche nach einem Polynom, welches genau durch die angegeben Werte geht. Die Problemstellung dabei ist, für n+1 gegebene Wertepaare $(x_{i},\,f_{i})$ mit paarweise verschiedenen Stützstellen $x_{i}$ ein Polynom $P$ maximal $n$-ten Grades zu finden. Beim Interpolationsproblem ist also $P$ im Vektorraum der Polynome mit Grad n oder kleiner zu suchen.

Lagrange-Interpolation

$\ell _{i}(x)=\prod _{\begin{smallmatrix}j=0\\j\neq i\end{smallmatrix}}^{n}{\frac {x-x_{j}}{x_{i}-x_{j}}}={\frac {x-x_{0}}{x_{i}-x_{0}}}\cdots {\frac {x-x_{i-1}}{x_{i}-x_{i-1}}}\cdot {\frac {x-x_{i+1}}{x_{i}-x_{i+1}}}\cdots {\frac {x-x_{n}}{x_{i}-x_{n}}}\,,$

die so definiert sind, dass

$\ell _{i}(x_{k})=\left\{{\begin{matrix}1&{\text{falls }}i=k\\0&{\text{falls }}i\neq k\end{matrix}}\right.$

gilt. Damit entspricht die Matrix $\left(\ell _{i}\left(x_{j}\right)\right)_{i,j=0,1,\dotsc ,n}$ genau der Einheitsmatrix.

Die Lösung des Interpolationsproblems lässt sich dann einfach angeben als

$P(x)=\sum _{i=0}^{n}f_{i}\ell _{i}\left(x\right)$

https://de.wikipedia.org/wiki/Polynominterpolation

Für unser Beispiel verwenden wir anstatt der Jahreszahlen 2011-2017 für $(i)$ die Zahlen 11,....,17, da diese Funktion bei Geogebra anschaulicher ist. Ansonsten wäre die Funktion um 2000 nach rechts verschoben.

Die Funktion sieht nun Folgendermaßen aus:

$f(x)={\frac {152028\cdot (x-12)\cdot (x-13)\cdot (x-14)\cdot (x-15)\cdot (x-16)\cdot (x-17)}{(11-12)\cdot (11-13)\cdot (11-14)\cdot (11-15)\cdot (11-16)\cdot (11-17)}}+{\frac {157333\cdot (x-11)\cdot (x-13)\cdot (x-14)\cdot (x-15)\cdot (x-16)\cdot (x-17)}{(12-11)\cdot (12-13)\cdot (12-14)\cdot (12-15)\cdot (12-16)\cdot (12-17)}}+{\frac {113471\cdot (x-11)\cdot (x-12)\cdot (x-14)\cdot (x-15)\cdot (x-16)\cdot (x-17)}{(13-11)\cdot (13-12)\cdot (13-14)\cdot (13-15)\cdot (13-16)\cdot (13-17)}}+{\frac {121519\cdot (x-11)\cdot (x-12)\cdot (x-13)\cdot (x-15)\cdot (x-16)\cdot (x-17)}{(14-11)\cdot (14-12)\cdot (14-13)\cdot (14-15)\cdot (14-16)\cdot (14-17)}}+{\frac {155847\cdot (x-11)\cdot (x-12)\cdot (x-13)\cdot (x-14)\cdot (x-16)\cdot (x-17)}{(15-11)\cdot (15-12)\cdot (15-13)\cdot (15-14)\cdot (15-16)\cdot (15-17)}}+{\frac {133520\cdot (x-11)\cdot (x-12)\cdot (x-13)\cdot (x-14)\cdot (x-15)\cdot (x-17)}{(16-11)\cdot (16-12)\cdot (16-13)\cdot (16-14)\cdot (16-15)\cdot (16-17)}}+{\frac {161613\cdot (x-11)\cdot (x-12)\cdot (x-13)\cdot (x-14)\cdot (x-15)\cdot (x-16)}{(17-11)\cdot (17-12)\cdot (17-13)\cdot (17-14)\cdot (17-15)\cdot (17-16)}}$

Fazit

Wie man sieht, ist diese Methode um Aussagen über die Zukunft zu machen nicht hilfreich. Die Funktion steigt ab dem Jahr 2017 sehr steil nach oben, was bedeuten würde, dass in den nächsten Jahren jährlich Hunderttausende neue Studenten dazu kommen, und wir in 50 Jahre viel zu viele Lehrpersonen hätten.

Der erste Zyklus ist hiermit beendet worden, da die Lagrange-Interpolation der falsche Ansatz war.

Zweiter Modellierungszyklus

Ziele

• anhand der Lehramtsstudenten auf die Lehrerzahl in der Zukunft schließen
• Lehramtsstudenten der Zukunft durch Regression berechnen

Durchführung

Gegeben sind die Studentenzahlen der Jahre 2011-2017. Mit Excel wurden durch Exponentielle, Logarithmische, Lineare, Polynome (2.,3.und 4. Grades) und Potenzielle Regression Funktionen für die Lehramtsstudentenzahl ausgeben. Diese wurden anschließend mit Geogebra als Graphen erstellt.

Lineare Regression

Die einfache Regression wird berechnet bzw. verwendet, wenn nur zwei Variablen betrachtet werden. Sei $y$ eine abhängige Variable, $y$ eine unabhängige und $v$=1,2,...,n.

y_v =a+bx_v

Die Formel sagt aus, dass y der Regresswert für die n-te Einheit ist. a und b sind Regressionskoeffizienten. a gibt den Ordinatenabstand und b die Steigung an.

Nichtlineare Regression

Die nicht lineare Regression wird berechnet, wenn eine abhängige Variable und mehrere unabhängige Variablen gegeben sind. Sie wird auch multiple Regression genannt mit n Regressoren.

y_v = b_0+b_1*x_1v+...+b_n*x_nv

Regression mit Excel

Im Folgenden wurden die Studentenzahlen in Excel eingetragen und mögliche Regressionen angewendet.

Anschließend wurden die Funktionen die Excel bei der Regression ausgegeben hat, in Geogebra eingegeben um die ganzen Funktionsgraphen zu sehen.

Die Funktionen wurden für die zukünftigen Jahre ausgewertet. (Diese Datei setzt sich aus drei Seiten zusammen.)

In Frankreich ist man nach 5 Jahren Studium fertig und lizensierte Lehrperson. Deshalb interessieren uns nur die Studentenzahlen bis zum Jahr 2063. Das Rentenalter von Lehrern liegt in Frankreich bei 57 Jahren. Lehrer die 57 Jahre alt sind, haben im Jahr 2029 angefangen zu studieren. Daher ist die Summe aller Studentenzahlen von 2029 bis 2063 relevant. Da nur 7,4% aller Studenten sich für die Lehrerlizenz anmelden, davon 9,6% nicht gewertet werden (wegen Betrugsversuch o.ä.), von den übrigen Gewerteten nur 70% bestehen, die Burnoutquote der Lehrer bei 3% liegt und wir das Ergebnis Runden, ergibt sich folgende Formel für EXCEL:

=Runden((Summe(C31:C65)*0,074*0,904*0,7*0,97);0)

Anhand dieser Formel haben wir die Lehreranzahl für das Jahr 2068 ausgerechnet. Durch diese Auswertung können die Polynomregressionen ausgeschlossen werden, da es keine negativen Lehrpersonenanzahl geben kann. Die Polynomregression zweiten Grades wäre ebenfalls nicht möglich, da es viel zu viele Lehrpersonen gäbe und diese auch nicht in den Universitäten ausgebildet werden könnten. Die übrigen vier Regressionen wären möglich. Da diese Region im Jahr 2068 79.659 Lehrpersonen bräuchte, erkennt man, dass es weniger Ausgebildete wären als benötigte.

Dritter Modellierungszyklus

Ziele

• anhand der aktuellen Lehrerzahlen durch Regression auf Lehrerzahlen in der Zukunft schließen

Im Folgenden wurden die Lehreranzahlen in Excel eingetragen und mögliche Regressionen angewendet.

Anschließend wurden Sie in Geogebra übertragen, um die gesamte Funktion zu sehen

Hinführung:

Wie auch schon bei der Studierenden werden die aktuellen Lehreranzahlen recherchiert, dazu mit Exel Graphen und Regressionen erstellt. Mit den Regressionsfunktionen wird die jeweilige Lehreranzahl ermittelt und ausgewertet. Bei der Auswertung fällt auf, dass die Polynomfunktionen wieder nicht stimmen können. Die Funktion vierten Grades ist wie bei den Studierenden negativ, die Funktionen zweiten und dritten Grades weisen eine viel zu hohe Lehreranzahl auf. Anders als bei dem zweiten Zyklus sind die Zahlen der Exponential- und lineare Funktion auch zu hoch. Somit kommen Logarithmus- und Potenzfunktion als Auswertung für die Zukunft in Frage. Der Fehler wäre sogar geringer als bei der Studentenregression. Dieser würde bei ca. +/- 2.000 Lehrpersonen liegen. Bei der Studentenauswertung wären es zwischen 20.000 und 11.000 Lehrpersonen, die fehlen würden.

Auswertung

Wenn beide Regressionen von den Lehrpersonen und den Studenten ermittelt werden, bemerkt man, dass die Daten von 2011-2017 mit den Regressionsauswertungen in diesen Jahren nicht komplett übereinstimmen. Dadurch wissen wir, dass wir einen bestimmten Fehlerwert in den Regressionsfunktionen beachten müssen. Dafür werden die Anzahlen der Lehrer/Studenten von 2011 bis 2017 zusammenbgerechnet und diese Summe mit der Anzahl der jeweiligen Regression verglichen. Stimmt sie nicht überein müssen wir die Werte, der Daten, die wir haben durch die jeweilige Summe einer Regression teilen und erhalten den prozentualen Fehlerwert in diesen Jahren. Bei der Regression von der Studentenzahl ausgehend wurde auch noch der Mittelwert berechnet. Da die Prozentzahlen so gering sind, ist der Mittelwert bei unseren eingeholten Daten und bei der logarithmischen und linearen Funktion identisch. Dadurch ist der Fehlerwert bei diesen Regressionen geringer als bei den anderen. Um den Fehler genauer zu definieren, werden die einzelnen Werte von 2011-2017 durch die jeweiligen Regressionswerte dividiert. Somit erhält man eine genauere Prozentzahl für jedes einzelne Jahr. Wenn man diese dann summiert und wieder durch sieben Jahre dividiert erhält man den eigentlichen Fehlerwert dieser Jahre. Zu erkennen ist nun, dass die Summe von den prozentualen Fehlerwerten größer ist, als nur vom Mittelwert.

Bei der Lehrerauswertung der Regressionen schwankt der Mittelwert ebenfalls sehr wenig. Somit werden auch hier die einzelnen Werte der Regressionen von 2011 bis 2017 durch einander dividiert, um den Fehlerwert in einer Prozentzahl zu erhalten. Wenn diese sieben Fehlerwerte miteinander addiert werden und durch sieben geteilt, erhält man auch hier einen genaueren Fehlerwert als den durch den Mittelwert.

Der Fehlerwert der Regressionen bei den Studenten und den Lehrpersonen ist nur für die ersten sieben Jahre berechnet worden. Man muss nun beachten, dass der Fehlerwert in den nächsten 50 Jahren weiter zunimmt oder abnimmt, je nach Änderung der Werte. Jedoch sollten wir mit den Werten der Regression und dem Fehleranteil im Jahr 2068 annähernd an die 79659 zu gebrauchten Lehrer kommen.

Ergebnis

Wenn die Fehlerwerte beider Regressionen miteinander verglichen werden, dann ist zu erkennen, dass der Fehlerwert bei den Lehrpersonen geringer ist als bei den Studenten. Dadurch wissen wir, dass die Lehrerregression uns genauere Zukunftsaussichten gibt. Bei der Studentenregression sollte man sich an der linearen Regression orientieren. Da wir nur Daten aus sieben unterschiedlichen Jahren hatten, konnte man nicht genau sagen, ob es die lineare Funktion ist. Durch die Auswertungen der Regressionen können wir davon ausgehen. Bei der Lehrerregression sind wir auch von sieben unterschiedlichen Jahren ausgegangen. Deswegen konnten wir auch da keine genau Regression festlegen. Wenn man die ausgewerteten Regressionen nun sieht, dann stellt man fest, dass bei den Lehrern die lineare Regression den kleinsten Fehlerwert aufweist, aber die Lehreranzahl dennoch viel zu hoch wäre. Da kommen die logarithmische und potenzielle Regression unseren Werten am nächsten. Der Fehlerwert der Potenziellen ist größer, als der der Logarithmischen. Deswegen würden wir uns an der Logarithmischen orientieren und erkennen, dass es im Jahr 2068 zu wenige Lehrpersonen gäbe.

(A3) Niveauzuordnung

Sekundarstufe 1

• Daten aus dem Internet recherchieren
• Gleichungen umstellen und lösen, um fehlende Daten zu errechnen
• Prozentrechnung
• Diagramme erstellen
• Informationen von Universitäten anfordern
• proportionale Zuordnung (Verhältnis Lehrer/Schüler)

Sekundarstufe 2

• Gleichungen erstellen und runden mit Excel
• aus Daten eine Funktion ablesen
• Potenzfunktionen, Populationsdynamik (Anzahl schulpflichtiger Kinder/Lehramtsstudenten in der Zukunft)

Uni

• anhand der Daten auf die Zukunft schließen (Vermutungen)
• Formeln erstellen die zur Zielführung beitragen
• Lagrange Interpolation
• Regression von nicht-linearen Funktionen
• Anwendung der Regression um Lehreranzahl 2068 zu berechnen

(A4) Sustainable Development Goals

• SDG11 Sustainable Cities and Communities

Die Population der Region nimmt aufgrund von Zuwanderungen immer weiter zu.

• SDG4 Quality Education

Durch die Schulpflicht müssen die Einwanderer auch unterrichtet werden. Die Lehrqualität in naher Zukunft in der Region soll erforscht und verbessert werden. Es sollen genügend Schulen und Lehrkräfte zur Verfügung stehen um die Massen von Schülern angemessen zu fördern.

• SDG8 Decent Work and Economic Growth

Die Bevölkerung wächst immer weiter, somit auch die Anzahl der schulpflichtigen Kinder als auch die Anzahl der Lehrkräfte.

• SDG9 Industry, Innovation and Infrastructure

Bei der steigenden Anzahl an SuS muss man auch darüber nachdenken mehr Schulgebäude und Universitäten zu bauen, als auch mehr Arbeitsplätze (Industrien) in denen die ganzen ausgebildeten jungen Erwachsenen dann arbeiten können.

(A5) Literatur

Engel, Joachim (2018): Anwendungsorientierte Mathematik: Von Daten zur Funktion. Eine Einführung in die mathematische Modellbildung für Lehramtsstudierende, Auflage 2, Springer Spektrum

(A6) Rohdaten

• Einwohnerzahlen

https://ec.europa.eu/eurostat/en/web/population-demography-migration-projections/statistics-illustrated
http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=demo_r_gind3&lang=en

• Gebrutenrate

https://ville-data.com/nombre-d-habitants/paca-93R
https://www.insee.fr/fr/statistiques/2012730#tableau-TCRD_044_tab1_regions2016
https://www.insee.fr/fr/statistiques/2012716#tableau-TCRD_010_tab1_regions2016
https://www.insee.fr/fr/statistiques/2012700#tableau-TCRD_013_tab1_regions2016
https://www.insee.fr/fr/statistiques/1405599?geo=REG-93
https://statistiques-locales.insee.fr/#c=indicator&i=evolpop.tx_var_pop&s=2010-2015&selcodgeo=93&view=map3
https://www.insee.fr/fr/statistiques/2012701#tableau-TCRD_005_tab1_regions2016

• Migrationszahlen

https://ec.europa.eu/eurostat/en/web/population-demography-migration-projections/migration-and-citizenship-data

• Schüler- und Lehrerzahlen PACA

http://www.ac-aix-marseille.fr/cid78855/archives-des-publications.html
http://www2.ac-nice.fr/cid128498/copie-de-les-chiffres-cles.html

• Studentenzahlen

http://cache.media.enseignementsup-recherche.gouv.fr/file/Panorama_recherche/09/9/le_potentiel_de_formation_660099.pdf

http://www.enseignementsup-recherche.gouv.fr/cid66020/les-etablissements-en-region-paca.html

http://cache.media.enseignementsup-recherche.gouv.fr/file/concertation/70/7/PlanEtudiantsWebDP_846707.pdf

http://cache.media.enseignementsup-recherche.gouv.fr/file/Panorama_recherche/53/9/Atlas_ES_2015_R93_604539.pdf

http://cache.media.education.gouv.fr/file/Donnees_essentielles/52/2/chiffres-essentiels_acnice_2017-2018_938522.pdf

http://cache.media.education.gouv.fr/file/Les_chiffres_cles/01/4/Etat_de_l_academie_18-19_ok_993014.pdf

http://www.cereq.fr/cereq/b265.pdf

http://www.ac-aix-marseille.fr/cid110607/la-mobilite-pour-les-eleves-et-les-etudiants.html

https://www.univ-amu.fr/system/files/2018-11/DEVE-c004-rapport_etude_qualitative_phase1_def_18_10_2012.pdf?q=system%2Ffiles%2F2018-11%2FDEVE-c004-rapport_etude_qualitative_phase1_def_18_10_2012.pdf

(A7) Modellierungsalternativen

• Um die Anzahl der schulpflichtigen Schüler heraus zu finden (und damit auch die Anzahl der benötigten Lehrkräfte) oft ein Durchschnitt von Daten benutzt, diese hätte man auch anhand von linearer Regression errechnen können damit die Zahlen am Ende etwas genauer sind.
  

• es wurde auch in fast jedem Schritt gerundet, man hätte auch alle Zahlen als Kommazahlen stehen lassen können und erst im letzten Schritt runden, damit das Ergebnis genauer ist
  

--> Nach dem Motto, so wenig Runden wie möglich, so oft wie nötig
--> am Ende Runden da es keine halben SuS und Lehrkräfte gibt