Sport und Mathematik im Kletterparkt

Die folgende Lernressource entstand aus der Überlegung, Aspekte der Schulmathematik an einem außerschulischen Lernort unter Zuhilfenahme (mathematischer) Apps digital und analog erleb- und erfahrbar zu machen. Der Besuch eines Kletterparks könnte als Exkursionsstädte im Rahmen eines Schulausfluges genutzt werden .
Der Kletterpark als mathematischen Lernort bietet sowohl den positiven Nutzen des außerschulischen Lernens als auch die Chance fächerübergreifendem Unterrichts. In diesem Beispiel wären sowohl Mathematik/ Physik, Sport und/ oder Informatik kombinierbar. Die Einbindung der digitalen Werkzeuge PyhPhox sowie LibreOffice Calc bietet darüber hinaus die Möglichkeit zur Förderung digitaler Kompetenzen. Des Weiteren ergeben sich durch die vorliegende Lernumgebung weitere positive Effekte auf den Bildungsprozess.
Kurz zu meiner Person: Mein Name ist Eric Schumacher und ich studiere an der Universität Koblenz-Landau gymnasiales Lehramt mit den Fächern Mathematik und Sport. Die Vorliegende Seite entstand begleitend zu meiner Masterarbeit mit dem Titel "Mathematik an außerschulischen Lernorten erleben und erfahren - Die App PhyPhox als digitales Werkzeug zum Verständnis der Differenzial- und Integralrechnung". Bei Fragen zu dem Unterrichtsvorhaben bzw. zum generellen Austausch verwandter Themen stehe ich gerne zur Verfügung, erreichbar bin ich unter ericschumacher@gmx.net.
Projekt
[Bearbeiten]Das auf dieser Seite gezeigte Unterrichtsvorhaben zielte auf folgende Fragestellung ab:
Inwiefern kann der außerschulische Lernort Kletterpark für fächerübergreifenden Unterricht der Bereiche Mathematik und Sport genutzt werden kann, um mithilfe der App PhyPhox die Konzepte der Differenzial- und Integralrechnung erleb- und erfahrbar zu gestalten.
Dazu werden einzelne kinematische Größen, die beim Klettern auftreten, mithilfe der von PhyPhox gemessen und dokumentiert. Die gewonnen Rohdaten können mithilfe einer Tabellenkalkulation , beispielsweise LibreOffice Calc, weiterverarbeitet werden, indem die Ableitungen bzw. "Aufleitungen"numerisch angenähert werden. Durch dieses Vorgehen lassen sich weitere kinematischen Größen darstellen. Dahinter steht die Absicht, dass die Schüler, die durch die neuen Daten entstandenen Graphen mit ihren Alltagserfahrungen von Bewegungsvorgängen verknüpfen und darüber hinaus ein tiefgreifendes Verständnis für die Differenzial- und die Integralrechnung gewinnen können.
Um vorab einen Überblick darüber zu erhalten, was am Ende dieses Prozesses als visuelles Ergebnis folgen könnte, werden mehrere Videos vorangestellt. In diesen werden nicht nur die Hindernisse sichtbar, an denen die Aktivitäten im Kletterpark gemessen wurden, es wird auch ersichtlich, wie sich die gewonnen Graphen sinnvoll einsetzten lassen. Die Videos zeigen die Aktivitäten sowohl aus der Sicht der Kletterers, als auch aus einer Außenperspektive.
Hindernis Seilrutsche:
Hindernis Quickjump Freefall:
Die Bewegungen in Kombination mit den Diagrammen zeigen erste Überschneidungen von Erlebtem und Gemessenen. Die Graphen können folglich gut genutzt werden, um damit die Alltagserfahrungen von Bewegungsvorgängen zu verknüpfen
Notwendigkeit
[Bearbeiten]Die Notwendigkeit eines solchen Unterrichtsvorhabens wird damit begründet, einem oftmals empfundenen monotonen, alltagsfernen und uninteressanten Unterrichtsalltag entgegenzustehen. Zudem sind Mathematikaufgaben der Differenzialrechnung laut einer einer Schulbuchanalyse von Dilling und Krause[1] weder authentisch, noch weißen sie eine Relevanz im Alltag der Schüler auf. Dazu beinhalten sie keine reelle bzw. idealisierte Daten. Diese Erkenntnis legitimiert die Entscheidung, dass Klassenzimmer zu verlassen um selbst reale und authentische Werte zu erfassen. Damit ergeben sich, wie in den folgenden Kapiteln noch herausgestellt wird, viele positive Einflüsse auf den Lernprozess.
Ablauf im Kletterpark
[Bearbeiten]Die Schüler sollen mithilfe ihrer Smartphones an vorher festgelegten Hindernissen bestimmte kinematische Größen messen, die während dem Klettern erlebt werden. Diese Messung geschieht mithilfe des digitalen Werkzeug PhyPhox. Das als App verfügbare Werkzeug muss dafür (am Besten bereits vorher in der Schule) auf den Endgeräten installiert worden sein. Eine Anleitung inkl. Installation und Anwendung von PhyPhox findet sich weiter unten (hier drücken). Für das Ausführen der Messungen wurden Experimente erstellt. Diese können innerhalb der App durch scannen eines QR-Codes auf den Smartphones aufgerufen und angewandt werden. Das Starten bzw. Enden der Experimente kann entweder von den Schülern selbst auf ihren Smartphones erledigt werden oder von einem Mitschüler, der der Fernzugriff auf die Anwendung zugreifen kann. Eine Anleitung dieser Vorgehensweise findet sich ebenfalls weiter unten (hier drücken, unter Punkt 3). Die gewonnenen Graphen uns Messwerte können unmittelbar nach der Ausführung am Hindernis angesehen werden. Das Erlebte kann direkt am Graphen nachvollzogen werden. Zurück in der Schule können aus den gemessenen Daten weitere kinematische Größen abgeleitet werden. Das Erstellen der Experimente sowie das Ergebnis dieser und Möglichkeiten zur Datenweiterverarbeitung finden sich im folgenden Abschnitt:
Experimente
[Bearbeiten]Für die Anwendung im Kletterpark wurden drei Experimente programmiert. Die ersten beiden messen jeweils eine kinematische Größe, die restlichen werden anhand der gemessenen ermittelt. Zu dem Vorgehen liegt eine ausführliche Beschreibung vor. Das dritte Experiment wurde erst im Anschluss an die Besuche im Kletterpark erstellt, weshalb von diesem Experiment keine Daten im Kletterpark vorliegen. Dieses Experiment gibt aber direkt auf dem Smartphone mehrere kinematische Größen gleichzeitig aus. Vor- und Nachteile der drei Versuche werden im Anschluss an dieses Kapitel erläutert
"Geschwindigkeit Seilrutsche"
[Bearbeiten]Das folgende Experiment soll die Geschwindigkeit einer Seilrutsche messen. Dabei ist es egal, wie lang und wie schnell die vorliegende Seilrutsche ist. Die folgenden Materialien sind aus einem Besuch im Kletterpark "FunForest" in Homburg entstanden.
Messwerkzeug/ Erstelltes Tool
[Bearbeiten]Das erstelle Werkzeug ist mithilfe des Editors auf der PhyPhox-Website programmiert worden. Eine Anleitung, wie das Experiment teil- und nutzbar ist, wird hier (Absatz 5) gegeben. Der benötigte QR ist:
 .
.
Dieses Experiment misst mithilfe von GPS-Daten des Smartphones indirekt die aktuelle Geschwindigkeit. Die Messdaten werden in der App in einem Geschwindigkeit-Zeit-Diagramm veranschaulicht. Die Messfrequenz beträgt 2 Hz. Das bedeutet, dass pro Sekunde zwei Mal die Geschwindigkeit gemessen wird.
Ausgabe der Daten auf dem Smartphone
[Bearbeiten]Das Anwenden des Experiments an einer Seilrutsche im Klettpark Homburg lieferte folgendes Geschwindigkeit-Zeit-Diagramm in der App PhyPhox:

Die gemessenen, unveränderten Rohdaten in tabellarischer Form können HIER aufgerufen werden:
Nach der Ausführung des Experiments ‚Geschwindigkeit der Seilrutsche‘ und durch das daraus resultierende v-t-Diagramm können die Schüler noch vor Ort den im Diagramm enthaltenen Graphen mit ihren eigenen Erfahrungen verbinden. Anhand gezielter Fragen, beispielsweise gestellt von der Lehrkraft oder bereits in das Experiment implementiert, können spezifische Bezüge zum Unterrichtsvorhaben hergestellt werden: Wie passt das persönlich Gefühlte zum Graphen? Wann war die Geschwindigkeit am höchsten bzw. wo liegt der Hochpunkt? Wie hängt die Höhe der Geschwindigkeit und ihre Dauer mit der zurückgelegten Strecke zusammen? Zu welchen Zeitpunkten wurde der Kletterer beschleunigt, wann abgebremst? Diesen Fragen kann im Kletterpark, bestenfalls unmittelbar nach der Ausführung, anhand des von PhyPhox erstellten Graphen in Verbindung mit dem persönlich Erlebten nachgegangen werden. Durch positive Emotionen und aktive Handlungen wird der Lernprozess bei den Schülern gefördert und die Inhalte besser im Gedächtnis gespeichert. Schüler, die selbst nicht klettern, können die oben gestellten Fragen durch ihre Beobachtungen ebenfalls beantworten, wenngleich hierbei die aktiv handelnde sowie affektive Komponente fehlt.
Weiterverarbeitung der Daten mittels LibreOffice Calc
[Bearbeiten]Die Rohdaten, die von der App generiert wurden, können an einen PC gesendet und mithilfe einer Tabellenkalkulation weiterverarbeitet werden. Dort können die Werte bzw. die Graphen der noch fehlenden kinematischen Größen errechnet bzw. erstellt werden. Für diese Arbeit wurde dazu das Programm LibreOffice Calc verwendet.
- Geschwindigkeit-Zeit-Diagramm:
Die dafür benötigten Daten liegen im Calc-Dokument durch die Messung im bereits vor. In der Spalte A befinden sich die Zeitpunkte [t in s], in der der Spalte B die dazugehörigen Geschwindigkeitswerte [v in m/s].

- Beschleunigung-Zeit-Diagramm:
Die Beschleunigung wird als Ableitung der Geschwindigkeit aufgefasst. Zur Annäherung an die Momentanbeschleunigung wird der Differenzialquotient auf zwei aufeinanderfolgende Wertepaare angewandt. Diese Rechnung wird in Calc mithilfe einer Formel im Eingabefeld ermöglicht. Formeln starten mit einem Gleichheitszeichen und anstatt der exakten Werte wird die Nummerierung der jeweiligen Zelle angegeben. Dieses Vorgehen wird auf alle Geschwindigkeit-Zeit-Wertepaare übertragen. 
- Ruck-Zeit-Diagramm:
Der Ruck ist die Änderungsrate der Beschleunigung. Die Annäherung dieser Größe erfolgt genau wie im vorherigen Fall.
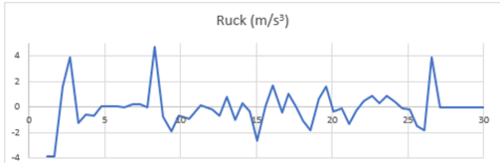
- Weg-Zeit-Diagramm:
Im Gegensatz zu den bisherigen kinematischen Größen müssen zur Annäherung an den zurückgelegte Weg vorhandene Daten nicht differenziert, sondern integriert werden. Dieses Vorgehen geschieht im mithilfe des Trapezverfahrens. Um eine exakte Lösung beim Integrieren zu erlangen, müssen dabei die Anfangsbedingungen bekannt sein. Da der Versuch so konzipiert wurde, dass unmittelbar zu Beginn der Aufzeichnung noch keine Bewegung ausgeführt werden soll, muss dementsprechend der Wert zum Start der Messung mit null festgelegt werden, also s(t0) = 0. Das Trapezverfahren verlangt in der Folge die Berechnung des Flächeninhalts des Trapezes, das durch die ersten beiden Geschwindigkeitswerte v(t_0 ) und v(t_1 ) und die dazugehörigen Zeitpunkte t0 und t1 aufgespannt ist. Dieser Wert wird anschließend zum bisherigen Weg addiert. Dadurch wird der Weg s(t1) approximiert, der bis zu dem Zeitpunkt t1 zurückgelegt wurde. Zur Berechnung werden beide Geschwindigkeitswerte addiert und durch zwei geteilt, wodurch ihr Mittelwert entsteht. Dieser Wert wird wiederum mit der Zeit-Differenz multipliziert und zum vorherigen Wert addiert, um den zurückgelegten Weg bis zum zweiten Zeitpunkt zu erhalten.
Die aus den errechneten Werten gewonnenen Diagramme sehen folgendermaßen aus:

Das Dokument mit den bearbeiten Daten kann HIER aufgerufen werden:
In dieser Datei sind auch die Formeln ersichtlich, die für den weiterverarbeiteten Daten verwendet wurden.
Herausstellen kinematischer Zusammenhänge in Kombination mit persönlich Erlebtem
[Bearbeiten]Anhand des Weg-Zeit-Diagramms können die Schüler ablesen, wie viele Meter sie zu welchem Zeitpunkt bereits zurückgelegt haben. Das Beschleunigung-Zeit-Diagramm hingegen gibt Auskunft über die Änderungsrate der Geschwindigkeit. Der Ruck kann mit dem Gefühl verbunden werden, das der Kletterer durch eine sich ändernde Beschleunigung wahrnimmt. Im Folgenden werden die Daten des Wegs, der Geschwindigkeit und der Beschleunigung mit dem subjektiv Erlebten abgeglichen. Dadurch lassen sich Zusammenhänge zwischen Stamm-, Ausgangs- und Ableitungsfunktion hervorheben. Zu diesem Zweck werden für Weg und Geschwindigkeit die approximierten Werte betrachtet, bei der Beschleunigung die des gleitenden Mittels. Dass bei der Beschleunigung nicht ebenfalls die reinen Approximationswerte zugrunde gelegt werden, ist dahingehend zu begründen, dass in den Daten starke Schwankungen festzustellen sind. Dies führt zu einer wesentlichen Abweichung von Erlebtem und Gemessenem. Der Rucks werden anschließend gesondert betrachtet.
Zum Startzeitpunkt des Experiments steht der Kletterer gesichert am Beginn der Seilrutsche bereit. Die Rohdaten zeigen dabei, dass der erste Messwert erst über eine Sekunde nach dem Start des Experiments erfasst wurde, obwohl durch die Einstellung von 2 Hz bereits frühere Datenpunkte hätten ermittelt werden sollen. Die dazugehörige Geschwindigkeit wurde mit dem Wert 0 korrekt aufgezeichnet, da noch keine Bewegung vorlag. Bei Sekunde 1,70 liegt der Wert bei 0,49 m/s. Somit ist eine leichte Diskrepanz des Erlebten mit dem Gemessenen zu erkennen, insofern sich der Kletterer zu diesem Zeitpunkt immer noch nicht fortbewegte. Die ersten Datenpunkte verdeutlichen zudem, dass vom Startzeitpunkt der Messung bis zum Start der Bewegung eine gewisse Zeit gewartet werden muss, damit eine Verbindung zu ausreichend vielen Satelliten gewährleistet werden kann. In der Zeitspanne, in der der Kletterer lediglich steht, wird ersichtlich, dass der Wert 0 bei der Ausgangsfunktion zum Wert 0 bei der Ableitung führt und keine Auswirkungen auf den Graphen der Stammfunktion festzustellen sind. Allerdings ist auch zu sehen, dass kleine Änderungen des Bestands zu großen Auswirkungen bei der Ableitung führen können.
Der Kletterer startet ab Sekunde 3,29 mit dem Rutschvorgang. In dieser Phase steigt sowohl der zurückgelegte Weg, die Geschwindigkeit als auch die Beschleunigung zunächst an. Der Geschwindigkeitsgraph verläuft bis Sekunde 15,08 streng monoton steigend. In diesem Zeitintervall wird der Zusammenhang zwischen Geschwindigkeit und zurückgelegtem Weg ersichtlich, denn je höher die Geschwindigkeit ist, desto schneller nimmt der zurückgelegte Weg zu bzw. desto steiler verläuft dessen Graph. Die Geschwindigkeit zwischen zwei Zeitpunkten bestimmt somit den zurückgelegten Weg. Die Beschleunigungswerte sind in der Phase der ansteigenden Geschwindigkeit stets positiv.
Während des Kletterns erlebt der Kletterer diese Werte am eignen Körper, da die Beschleunigung mit verschiedenen Sinnen wahrzunehmen ist: Die Rollen des Sicherungssystems, mit denen der Kletterer an der Seilrutsche befestigt ist, gleiten während der Fahrt entlang des Stahlseils. Da das Ende des Seils niedriger liegt als der Startpunkt, wird der Kletterer aufgrund der Erdanziehungskraft entlang des Stahlseils nach vorne gezogen. Die positive Beschleunigung bzw. der daraus resultierende Ruck wird vom Kletterer dahingehend gespürt, dass er leicht entgegen die Fahrtrichtung gedrückt wird. Das Ansteigen der Geschwindigkeit empfindet der Kletterer nicht nur durch einen scheinbar auftretenden und stärker werdenden Gegenwind, sondern die Wahrnehmung wird durch den akustischen Sinneseindruck der Rollen beim Drehen über das Stahlseil verstärkt. Mit ansteigender Geschwindigkeit wird dieser Ton höher und lauter.
Bei Sekunde 15,08 erreicht der Kletterer mit 10,5m/s2 seine maximale Geschwindigkeit, was dem Hochpunkt des Graphen entspricht. Weil zu diesem Zeitpunkt auch der Zuwachs des Wegs am höchsten ist, erreicht der Graph im Weg-Zeit-Diagramm seine höchste Steigung. Der Verlauf der Graphen des Wegs, der Geschwindigkeit sowie der Beschleunigung verdeutlicht hierbei, dass der Hochpunkt der Ausgangsfunktion mit dem Wendepunkt der Stammfunktion und einer Nullstelle der Ableitungsfunktion einhergeht. Von diesem Zeitpunkt an verläuft der Graph der Geschwindigkeit bis zum Ende des Experiments monoton fallend. Verringert sich die Geschwindigkeit, wird in dieser Zeit entsprechend weniger Weg zurückgelegt. Die Steigung des Graphen im Weg-Zeit-Diagramm verläuft flacher. Die Werte der Beschleunigung liegen bis zum Ende der Bewegung im negativen Bereich. Die negative Beschleunigung, also das Bremsen, spürt der Kletterer ebenfalls. Die Rollen am Stahlseil gleiten, u. a. aufgrund des Rollwiderstands und der nicht mehr abfallenden Höhe, immer langsamer entlang des Seils. Der Kletterer selbst bewegt sich allerdings noch mit der vorherigen, höheren Geschwindigkeit fort und schwingt dementsprechend leicht nach vorne. Dadurch spürt er die kinematische Größe des Rucks. In der Phase der negativen Beschleunigung wird ebenso das Geräusch, das die Rollen des Sicherungssystems beim Drehen über das Stahlseil erzeugen, leiser und der empfundene Gegenwind nimmt stetig ab. Der Kletterer erreicht bei Sekunde 26,59 die Plattform am Ende der Seilrutsche. Es findet anschließend keine Bewegung mehr statt, wodurch die Geschwindigkeit auf null fällt. Folglich sind weder Gegenwind noch die Geräusche der Rollen als Sinneseindrücke festzustellen. Der Graph im Weg-Zeit-Diagramm verläuft ab diesem Zeitpunkt konstant. Die approximierte Länge der Seilrutsche kann abschließend am Maximum des monoton steigenden Graphen im Weg-Zeit-Diagramm abgelesen werden, die laut Daten bei 134,44 Metern liegt. Vor den Messungen abgegebene Schätzungen der Schüler bzgl. der Länge der Seilrutsche können somit verglichen und kontrolliert bzw. die Ergebnisse der Approximation auf deren Sinn überprüft werden. Laut Angaben eines Mitarbeiters des Kletterparks beträgt die Seillänge zwischen Start- und Endpunkt 150 Metern. Somit liegt eine Abweichung von ca. 10 % vor. Unter Berücksichtigung der vorgenommenen indirekten Messung sowie der Approximation der Daten ist dieser Wert eine gute Annäherung an die Realität. Die Datenaufzeichnung endet schließlich mit dem Messzeitpunkt bei Sekunde 30,98.
Bei der bisherigen Betrachtung wurden die Werte des Rucks noch nicht berücksichtigt. Dies ist damit zu begründen, dass sich sein Maß während des gesamten Verlaufs nicht mit dem Erlebten deckt, weder vor noch nach Anwendung des gleitenden Mittels. Die Daten pendeln, unabhängig davon, ob eine positive oder negative Beschleunigung vorlag, im Bereich zwischen −2 und 2 m/s3 mehrmals hin und her. Sie sind somit für das Verbinden von Erlebtem und Gemessenem unbrauchbar. Die Werte müssten im groben Verlauf das Gespürte folgendermaßen widerspiegeln: Zu Beginn der Bewegung liegen aufgrund der ansteigenden Beschleunigung positive Werte des Rucks vor. Zu diesem Zeitpunkt ist der Ruck aufgrund der Trägheitskräfte zu spüren, indem der Kletterer gefühlt leicht nach hinten gedrückt wird. Nachdem der Hochpunkt der Beschleunigung überwunden ist, befinden sich die Werte des Rucks leicht im negativen Bereich. Während der Kletterer schrittweise seine Höchstgeschwindigkeit erreicht, nähern sich die Daten immer weiter dem Wert 0 an. In dieser Zeitspanne ist für den Kletterer kein Ruck wahrzunehmen. Zu Beginn des Bremsvorgangs liegen erneut negative Werte vor und der Kletterer wird leicht nach vorne gedrückt. Die Werte verlaufen bis zum Erreichen der Endposition erst positiv, bevor sie sich wieder der Null annähern.
Schwierigkeiten bei der Messwerterfassung
[Bearbeiten]Viele Kletterparks befinden sich in Waldgebieten. Daher ist bei der GPS-Messung darauf zu achten, dass nach dem Start des Experiments einige Sekunden gewartet wird, damit eine Verbindung mit ausreichend vielen Satelliten hergestellt werden kann, die zur Erfassung notwendig ist. Aufgrund dessen ist darauf zu achten, dass nach dem Start der Messung mehrere Sekunden gewartet wird, bis der Kletterer mit dem Rutschvorgang beginnt.
"Quickjump Freefall"
[Bearbeiten]Das folgende Experiment misst den Höhenunterschied, der bei einem Sprung von einer Plattform in die Tiefe in vertikaler Richtung zurückgelegt wird. Die Messung geschieht per integriertem Barometer über den Luftdruck. Zu Beginn des Experimentes ergibt sich aus dem Luftdruck, welcher in der Umgebung des Geräts herrscht, eine Höhe. Die Höhe wird allerdings nicht mit der Höhe ü.NN, sondern zunächst mit 0 angegeben. Springt man nun in die Tiefe, errechnet das Gerät aus dem sich verändertem Luftdruck, welcher Höhenunterschied zurückgelegt wurde. Dabei ist es egal, von welcher Höhe man "springt", selbst Messungen aus einem Meter Höhe werden adäquat aufgezeichnet. Die folgenden Materialien sind aus einem Besuch im Kletterpark "FunForrest" in Kandel entstanden.
Messwerkzeug/ Erstelltes Tool
[Bearbeiten]Das erstelle Werkzeug zur Messung des Höhenunterschieds bei einem Sprung in die Tiefe ist mithilfe des Editors auf der PhyPhox-Website programmiert worden. Eine Anleitung, wie das Experiment teil- und nutzbar ist, wurde HIER gegeben. Der benötigte QR ist:

Ausgabe der Daten auf dem Smartphone
[Bearbeiten]Das Anwenden des Experiments an einer Seilrutsche im Klettpark Homburg lieferte folgendes Geschwindigkeit-Zeit-Diagramm in der App PhyPhox:
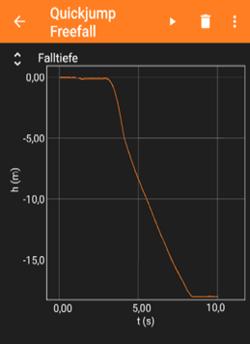
Die gemessenen, unveränderten Rohdaten in tabellarischer Form können HIER Link aufgerufen werden:
Das nach der Ausführung generiete s-t-Diagramm kann unmittelbar mit den eigenen Erfahrungen verbunden werden. Anhand des Graphen ist beispielsweise die Höhe, aus der abgesprungen wurde, direkt abzulesen. Dieser Wert liegt bei 19,50 m und kann mit einer vorherigen Schätzung verglichen werden. Er kommt dabei nahe an die Angabe der Homepage des Kletterparks heran, laut der die Höhe 20 Meter beträgt. Ebenso ist die Dauer der Bewegung direkt ersichtlich. Von Absprung bis Landung sind knapp sechs Sekunden vergangen. Anhand gezielter Fragen seitens der Lehrperson können die Schüler mithilfe des Graphen und des Erlebten Bezüge herstellen, die auf die Analysis abzielen: Wie hat sich während des Sprungs deine Geschwindigkeit verändert? Wann war die Geschwindigkeit wohl am höchsten? In welchen Zeitspannen wurdest du beschleunigt, wann abgebremst? Diese Fragen sind zudem unter dem Menüpunkt ‚Info‘ im Experiment implementiert. Die Lernenden können sie durch ihr Erlebtes beantworten und anschließend die jeweiligen Punkte im Weg-Zeit-Diagramm wiederzufinden. Auch Schüler, die selbst nicht klettern, können die Fragen allein durch ihre Beobachtung beantworten.
Weiterverarbeitung der Daten via LibreOffice Calc
[Bearbeiten]Die Rohdaten, die von der App generiert wurden, können an einen PC gesendet und mithilfe einer Tabellenkalkulation weiterverarbeitet werden. Dort können die Werte bzw. die Graphen der noch fehlenden kinematischen Größen errechnet bzw. erstellt werden. Dafür wurde wieder das Programm LibreOffice Calc verwendet.
- Weg-Zeit-Diagramm:
Die dafür benötigten Daten liegen im Calc-Dokument durch die Messung im bereits vor. In der Spalte A befinden sich die Zeitpunkte [t in s], in der der Spalte B die dazugehörigen Werte der Höhe [h in m].

- Geschwindigkeit-Zeit-Diagramm:
Die Geschwindigkeit wird als Ableitung des Wegs aufgefasst. Zur Annäherung an die Momentangeschwindigkeit wird der Differenzialquotient auf zwei aufeinanderfolgende Wertepaare angewandt. Diese Rechnung wird in Calc mithilfe einer Formel im Eingabefeld ermöglicht. Das Vorgehen wurde im 1. Experiment bereits erläutert, weshalb auf eine erneute Anleitung verzichtet wird.
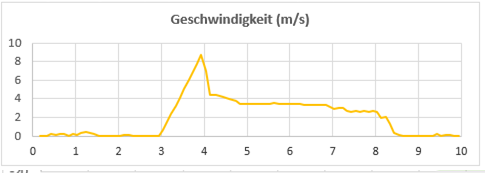
- Beschleunigung-Zeit-Diagramm:
Die Beschleunigung wird als Ableitung der Geschwindigkeit aufgefasst. Zur Annäherung an die Momentangeschwindigkeit wird der Differenzialquotient auf zwei aufeinanderfolgende Wertepaare angewandt.
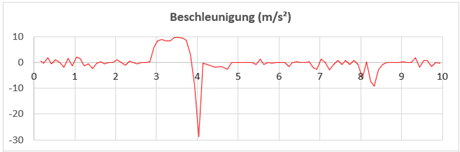
- Ruck-Zeit-Diagramm:
Der Ruck ist die Änderungsrate der Beschleunigung
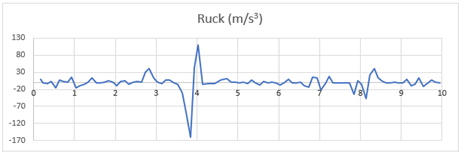
Das Dokument, in dem die neuen Werte vorliegen findet sich HIER:
Dort sind auch die Formeln zu sehen, die zur Berechnung benutzt wurden.
Herausstellen kinematischer Zusammenhänge in Kombination mit persönlich Erlebtem
[Bearbeiten]Zu Beginn der Datenaufzeichnung befindet sich der Kletterer abgesichert und sprungbereit auf der Plattform des Hindernisses Quickjump Freefall. Bis Sekunde 3 schwanken die Höhenwerte im Bereich von zehn Zentimetern, faktisch findet jedoch keine Bewegung statt. In dieser Zeitspanne steht der Kletterer still auf der Plattform und spürt weder Geschwindigkeit, Beschleunigung noch Ruck. Dass die dazugehörigen Werte jedoch von null abweichen, liegt an dem leichten Rauschen der Höhenwerte. Fälschlicherweise sorgen diese dafür, dass Geschwindigkeitswerte zwischen 0,00 und 0,45 m/s und Beschleunigungswerte zwischen −1,33 und 0,84 m/s2 approximiert werden. Vor dem Hintergrund der Differenzialrechnung lässt sich in dieser Phase festhalten, dass ein konstanter Verlauf der Ausgangsfunktion bei der ersten sowie zweiten Ableitung den Wert 0 erzeugt. Unmittelbar nach dem Absprung erlebt der Kletterer aufgrund der Konstruktion des Hindernisses einen rasanten Abstieg. Folglich ist die Bewegung auch im Graphen ersichtlich, indem die Höhe zunächst stark abfällt. Laut Datensatz beginnt der Absprung ab Sekunde 3,03. Obwohl sich die Höhe bis zum nächsten Messzeitpunkt zwar nur um etwas weniger als 0,10 m verringert, macht sich dies in der Beschleunigung mit einem Wert von 7,79 m/s2 bemerkbar. Vom Moment des Absprungs bis zu Sekunde 3,83 ähnelt der Verlauf des Graphen im Weg-Zeit-Diagramm dem rechten Ast einer nach unten geöffneten Parabel. In diesem Zeit-Intervall liegen die Beschleunigungswerte vor der Anwendung des gleitenden Mittels im Bereich von 8,35 und 9,73 m/s2, die Geschwindigkeit steigt dabei annähernd linear von 0,64 auf 7,88 m/s. Unter Berücksichtigung des Rauschens der gemessenen Höhenwerte kann in dieser Phase von einer gleichförmig beschleunigten Bewegungen gesprochen werden. Die approximierten Beschleunigungswerte liegen dabei nur knapp unter der Erdanziehungskraft von 9,81 m/s2. Die geringe Abweichung könnte durch den vorhandenen Luftwiderstand begründet sein. Dennoch sprechen die Daten dafür, dass bei diesem Hindernis zwischen Sekunde 3,03 und 3,73 ein freier Fall erlebt wurde. Dies deckt sich mit den Erfahrungen, die während des Sprungs gemacht wurden. Im Kontext der Differenzialrechnung sind die Diagramme aus der Zeitspanne des freien Falls anschaulich nutzbar: Es wird ersichtlich, dass ein parabelförmiger Verlauf der Ausgangsfunktion in deren Ableitung zu einer Geraden wird. Wird die Grade wieder abgeleitet, also die Ableitung der Ableitung gebildet, entsteht ein konstanter Verlauf ungleich null. Überdies lässt sich ein weiterer Zusammenhang zwischen Ausgangs- und Ableitungsfunktion feststellen: Je steiler die Ausgangsfunktion ist, desto höher fällt der Wert der Ableitung aus. Etwa bei Sekunde 4 erreicht der Graph des Weg-Zeit-Diagramms sein maximales Gefälle, was bezogen auf die Analysis dem Wendepunkt entspricht. Anhand der Daten lässt sich erkennen, dass diese Stelle mit einem Extrempunkt der Geschwindigkeit einhergeht. Unmittelbar danach setzt die magnetische Bremstechnologie des Hindernisses ein. Diese sorgt zunächst für ein kurzzeitiges starkes Abbremsen des Kletterers. Währenddessen ist im Graphen der Geschwindigkeit ein starkes Abfallen nach unten ersichtlich. Die Beschleunigungswerte werden in dieser Zeitspanne mit bis zu −11,47 m/s2 angegeben. Die negative Beschleunigung, also das Bremsen, spürt der Kletterer, indem sich seine Geschwindigkeit ruckartig verringert.
Aufgrund des starken Abbremsens sowie des damit einhergehenden Rucks wird im vorliegenden Fall der Körper des Kletterers nach unten gedrückt. Im dazugehörigen Video wird ersichtlich, dass dadurch die Beine des Kletterers entgegen der Fallrichtung nach oben gedrückt werden. Nach dem Abbremsen wird der Kletterer für mehrere Sekunden kontrolliert nach unten geführt. Die Höhe fällt zwischen Sekunde 4,13 und 8,03 annähernd linear von −5,43 auf −18,66 m. Die Geschwindigkeit verläuft in diesem Zeitraum beinahe konstant, leicht abfallend von 4,44 auf 2,62 m/s2. Gleichzeitig bewegen sich die Beschleunigungswerte um den Wert 0 bzw. knapp darunter. Hier werden erneut die Zusammenhänge zwischen Ausgangsfunktion und ihren Ableitungen gut ersichtlich. Aufgrund der kinematischen Werte kann nach dem Bremsvorgang von einer gleichförmig geradlinigen Bewegung gesprochen werden. Auch akustisch lässt sich eine solche wahrnehmen, denn das magnetische Bremssystem gibt aufgrund des gleichmäßigen Ausrollens des Seils in dieser Zeitspanne ein monotones Geräusch wieder. Erst, wenn sich das Ausrollen verlangsamt, wenige Augenblicke bevor der Ketterer den Boden erreicht, wird dieses Geräusch leiser. Der hörbare Unterschied geht mit einem zweiten Bremsvorgang einher. Der Kletterer wird dadurch sanft zu Boden gebracht, womit eine harte Landung vermieden und das Verletzungsrisiko minimiert wird. Im Weg-Zeit-Diagramm wird die weiche Landung durch den leicht gekrümmten Verlauf des Graphen ersichtlich. Von Sekunde 8,13 bis 8,53 fällt die Geschwindigkeit von 1,99 auf annähernd 0 m/s2. Die Geschwindigkeit verringert sich somit langsam, bis schließlich keine Höhenänderung mehr vorliegt. Folge der absteigenden Geschwindigkeitswerte sind erneut negative Beschleunigungswerte, deren Extremwert in diesem Fall bei −6,42 m/s² liegt. Dieser Bremsvorgang ist folglich wesentlich sanfter als der erste, was sich neben den Daten auch in den gespürten Kräften widerspiegelt. Beide Bremsvorgänge zeigen überdies, dass ein Abfallen der Geschwindigkeit mit negativen Beschleunigungswerten einhergeht. Der Graph im Weg-Zeit-Diagramm hat zum Zeitpunkt der Landung sein Minimum bei −19,5 m erreicht. Bis zur Beendigung des Experiments schwankt der Wert im Bereich von ±0,02 m. Diese geringen Änderungen lassen sich wiederum durch das Rauschen der Messwerte erklären. Ähnlich wie vor dem Absprung variieren die Werte der Geschwindigkeit und der Beschleunigung dadurch ebenfalls, obwohl der Kletterer keine Bewegung mehr vornimmt. Die Werte des Rucks schwanken bei diesem Experiment im Vergleich zu ‚Geschwindigkeit der Seilrutsche‘ zwar ebenfalls, jedoch sind im Verlauf des Graphen die relevanten Stellen deutlich zu erkennen: Vor allem bei der positiven Beschleunigung während des freien Falls sowie beim ersten und beim zweiten Bremsvorgang sind hohe Ausschläge im Graphen zu erkennen, was sich wiederum im Kontext des persönlichen Erlebens während des Parcours widerspiegelt. Die Anwendung des gleitenden Mittels hat in diesem Fall dafür gesorgt, dass viele Oszillationen geglättet werden, wodurch Abweichungen vom Erlebten eliminiert werden konnten.
Beim Erstellen der Diagramme sowie ihrer Auswertung besteht, wie bereits beim vorherigen Experiment, der Vorteil, dass für die Schüler Erlebtes durch die Daten quantifiziert und sichtbar wird. Bei der Interpretation der gewonnenen Daten muss jedoch bedacht werden, dass im gezeigten Beispiel die Beträge der Geschwindigkeitswerte berechnet wurden. Der Kletterer spürt nach dem Absprung, wie sich seine Geschwindigkeit während des Falls erhöht. Jedoch entstehen durch das Differenzieren der fallenden Höhenwerte negative Geschwindigkeitswerte. Gegensätzlich dazu nimmt der Kletterer diese Geschwindigkeit allerdings als positiven Wert wahr. Damit dieses Gefühl mit den Daten übereinstimmt, wurden dementsprechend die Beträge der Geschwindigkeit berechnet und somit negative Werte vermieden. Ein weiterer Vorteil dieser Herangehensweise ergibt sich bezogen auf die Betrachtung der Ableitung der Geschwindigkeit: Negative Beschleunigungswerte gehen mit einem Bremsvorgang einher, positive Werte dementsprechend mit einer Zunahme der Geschwindigkeit. Das Verwenden der Beträge könnte vermieden werden, indem das Experiment so programmiert wird, dass der beim Sprung überwundene Höhenunterschied mit positiven anstatt negativen Vorzeichen erfasst wird. Am vorliegenden Hindernis würde der daraus resultierende Graph somit monoton steigend verlaufen. Auch diese Variante ist ebenso denkbar und richtig. Die Entscheidung fiel jedoch gegen diese Option, da der monoton fallende Graph im Weg-Zeit-Diagramm die Bewegungsrichtung des Kletterers verdeutlicht und anschaulich abbildet.
Schwierigkeiten bei der Messwerterfassung
[Bearbeiten]- Da der Luftdruck an einem festen Ort durch Temperatur und Wetterlage jedoch schwankt, kann die daraus errechnete Höhe verfälscht werden.
- Ursprünglich sollte für dieses Hindernis zusätzlich der integrierte Beschleunigungssensor in vertikaler Richtung angewandt werden. Durch zweifache Integration der Beschleunigungswerte hätte auf die überwundene Höhe geschlossen werden können. In diesem Zusammenhang wäre der Vergleich dieses Werts mit den Daten, die mithilfe des Barometers errechnet wurden, möglich. Vor dem Hintergrund, dass beide Zugänge voneinander unabhängige Sensoren benötigen, wäre eine Diskussion dieser Ergebnisse besonders interessant gewesen. Allerdings lieferte der Beschleunigungssensor, dessen Funktionsweise in Kapitel 5.2 beschrieben wurde, bei mehreren Versuchen keine sinnvollen Daten. Beschleunigungswerte werden bei der Anwendung, bezogen auf die Ausrichtung des Smartphones, getrennt nach den Achsen im dreidimensionalen Raum angegeben. Um die Beschleunigung in vertikaler Richtung zu dokumentieren, muss das Smartphone während der gesamten Messung waagrecht zum Boden und mit dem Display nach oben positioniert werden. Geschieht dies nicht oder dreht sich das Gerät während der Bewegung, wird u. a. die Fallbeschleunigung immer wieder in anderen Richtungen gemessen, wodurch die gemessenen Daten unbrauchbar werden. Da die benötigte Ausrichtung des Geräts während des gesamten Sprungvorgangs jedoch nicht realisierbar war, wurde diese Überlegung wieder verworfen. Dennoch wäre es möglich, eine geeignete Konstruktion zu bauen, um damit eine zielführende Messung zu ermöglichen. Dafür müsste das Smartphone lediglich so am bzw. auf dem Helm befestigt werden können, dass das Display stets nach oben ausgerichtet ist.
"Kinematische Größen durch Differenziation"
[Bearbeiten]Dieses Experiment ist angelehnt an "Quickjump Freefall", denn der Höhenunterschied wird ebenfalls mittels Barometer gemessen. Allerdings wird aus diesen Werten - direkt innerhalb der App - die Geschwindigkeit sowie die Beschleunigung abgeleitet und grafisch veranschaulicht. Somit ist für die Weiterverarbeitung dieser Daten keine Tabellenkalkulation nötig.
Durch scannen des folgenden QR-Codes kann das Experiment auf der App abgerufen werden.

Allerdings wurde dieses Experiment erst nach den Besuchen in den Kletterparks programmiert. Somit liegen keine Daten am Hindernis vor. Zur Veranschaulichung der Datenausgaben wurde das Experiment zuhause ausgeführt. Dabei wurde das Smartphone nach dem Start von "Kinematische Größen durch Differenziation" mehrmals in die Höhe gehalten und langsam zu Boden geführt. Auf dem Bildschirm wurden folgendes ersichtlich:
Vor- und Nachteile der einzelnen Experimente
[Bearbeiten]| - | "Geschwindigkeit der Seilrutsche | "Quickjump Freefall" | "Kinematische Größen durch Differenziation" |
|---|---|---|---|
| VORTEILE | Differenzial- und Integralrechnung möglich | Ruck nutzbar/ Messung kann immer direkt gestartet werden | kein PC zur Weiterverarbeitung nötig |
| NACHTEILE | keine Messung wenn GPS-Verbindung fehlt/ Ruck nicht nutzbar | nur Differenzialrechnung möglich | geringer Erwerb digitaler Kompetenzen |
Chancen und Herausforderungen des außerschulischen Lernortbesuchs
[Bearbeiten]Das Verlassen des Klassenzimmers sollte immer in Hinblick auf deine Chancen begründet werden und sollte nie zum reinen Selbstzweck werden. Allerdings gehen mit einem außerschulischen Lernortbesuch auch Herausforderungen einher, welche von der Lehrkraft in die Entscheidungsfindung eines passenden Lernortes beachtet werden müssen.
Vorteile für den Mathematikunterricht:
[Bearbeiten]KOMPETENZEN:
• Mathematisch argumentieren (K1): Durch die entdeckten Zusammenhänge der verschiedenen kinematischen Größen, welche sowohl gemessen als auch erlebt wurden, sind die Schüler in der Lage, mathematischer Aussagen zu verstehen und zu bewerten.
• Probleme mathematisch lösen (K2): Die Kompetenz wird dahingehend gefördert, indem die Schüler mit dem Differenzenquotienten bzw. Differenzialquotienten und der Trapezregel Verfahren anwenden können um Ableitungen und Integrale berechnen zu können. Die Lernenden können somit „einen Lösungsweg einer einfachen mathematischen Aufgabe durch Identifikation und Auswahl einer naheliegenden Strategie finden“.
• Mathematisch modellieren (K3): Durch den Wechsel zwischen erlebter Realsituationen im Kletterpark und mathematischen Berechnungen via Calc können die Schüler ein mathematisches Resultat auf eine gegebene Realsituation übertragen sowie dessen Ergebnisse interpretieren.
• Mathematische Darstellungen verwenden (K4): Durch den zielgerichteten Einsatz einer Tabellenkalkulation fördern die Schüler ihre Kompetenzen hinsichtlich der Auswahl geeigneter Darstellungsformen sowie dem Erstellen mathematischer Darstellungen. Dazu gehören sowohl Diagramme, Graphen, Tabellen als auch Formeln. Anforderungsbereich. Darüber hinaus können sie die Darstellungen interpretieren bzw. eigene Darstellungen problemadäquat entwickeln.
• Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen (K5): Zuletzt wird durch die Anwendung der App PhyPhox in Verbindung mit einer Tabellenkalkulation auch der sinnvolle und verständige Einsatz von mathematischen Werkzeugen gefördert. Die Lernenden können diese Hilfsmittel nutzen und formale mathematische Verfahren der Tabellenkalkulation anwenden. Darüber hinaus können sie die Grenzen mathematischer Verfahren, Hilfsmittel und digitaler Mathematikwerkzeuge reflektieren. Diese zeigen sich beispielsweise während der Grenzwertbildung diskreter Messwerte oder bei der beschränkten Messfrequenz einiger Sensoren.
LEITIDEEN:
• Messen: Diese mathematische Leitidee wird dahingehend gefördert, dass die Schüler durch die beschriebenen Aktivitäten befähigt werden, Sekanten- und Tangentensteigungen an Graphen zu bestimmen, Änderungsraten zu berechnen und deuten sowie Inhalte von Flächen, die durch Funktionsgraphen begrenz sind, zu ermitteln.
• funktionaler Zusammenhang: Die Schüler können die Verknüpfungen von Graphen zur Beschreibung quantifizierbarer Zusammenhänge nutzen. Darüber hinaus sind sie in der Lage, die Ableitung insbesondere als lokale Änderungsrate zu deuten, die Änderungsraten funktional zu beschreiben und interpretieren sowie den Ableitungsgraphen zur Bestimmung von Extrema zu nutzten. Ebenso können sie den Ableitungsgraphen aus dem Funktionsgraphen und umgekehrt entwickeln, das bestimmte Integral, insbesondere als rekonstruierten Bestand, zu deuten und geometrisch-anschaulich den Hauptsatz der Differenzial- und Integralrechnung als Beziehung zwischen Ableitungs- und Integralbegriff zu begründen.
• Algorithmus und Zahl: Die Vorstellung reeller Zahlen wird hin zu Annäherungen mittels infinitesimaler Methoden erweitert. Somit können sie Schüler Grenzwerte auf der Grundlage eines propädeutischen Grenzwertbegriffs insbesondere bei der Bestimmung von Ableitung und Integral nutzen
Vorteile für den Sportunterricht:
[Bearbeiten]- Teambuilding-Maßnahme
- Sozialkompetenz durch gegenseitige Hilfestellungen
- Möglichkeit zum "lebenslangem Sporttreiben"
- Erwerb, die Erweiterung sowie die Verbesserung motorischer Fähigkeiten und Fertigkeiten
- Entwicklung der Wahrnehmungsfähigkeit für körperliche sowie psychische Reaktionen
- Aufgezählter Listeneintrag
allgemeine Vorteile:
[Bearbeiten]- Primärerfahrungen
- Affektive Komponente
- Fächerübergreifender Unterricht (Sport, Mathematik, Physik, Informatik etc.)
- Das Vorhaben ist für viele Schüler unterschiedlicher Altersstufen und Leistungsniveaus zugänglich
- Möglichkeiten zur Inklusion (werden später in einem separatem Abschnitt erläutert)
Herausforderungen
[Bearbeiten]- hoher Zeitaufwand für Lehrkräfte
- das Vorhaben benötigt inkl. Vor- und Nachbereitung viel Unterrichtszeit
- technische Voraussetzungen der Schülergeräte müssen erfüllt sein
- Vorhandensein von PC-Räumen in der Schule
- Was machen Schüler, die aufgrund von psychischen oder physischen Gründen nicht Klettern können?
PhyPhox - Das Smartphone als Messinstrument
[Bearbeiten]PhyPhox wurde von Mitarbeitern des 2. Physikalischen Instituts der RWTH in Aachen als digitales Werkzeug zur attraktiven und modernen Naturwissenschaftsbildung für den Schulunterricht, aber auch für ein vielfältiges Lernen außerhalb der Institution Schule entwickelt. Die Bezeichnung PhyPhox ist ein Akronym für physical phone experiments physical phone experiments. Die App ist kosten- und werbefrei sowohl für Android als auch für iOS nutzbar. Sie ermöglicht eine schülergerechte Durchführung von Experimenten und Messungen mit Hilfe integrierter Smartphone-Sensoren. Nutzbar sind die Sensoren Beschleunigung, Gyroskop, Magnetfeld, Licht, Magnetfeld, GPS, Temperatur, Druck, Luftfeuchtigkeit undund
Die nachfolgende Anleitung ist zum einfacheren Umgang mit der App phyphox erstellt worden, dabei werden die wichtigen Funktionen und ihre Bedienung erläutert:
1. Installation der App
[Bearbeiten]PhyPhox ist kosten- als auch werbefrei sowohl für iOS als auch Android im jeweiligen App-Store downloadbar.
Link für iOS: https://apps.apple.com/de/app/phyphox/id1127319693
Link für Android: https://play.google.com/store/apps/details?id=de.rwth_aachen.phyphox&hl=de&gl=US
2. Erste Schritte in PhyPhox
[Bearbeiten]- Öffnen der App
- Wahl eines definierten Experimentes im Hauptmenü
- Start der Messung
3. Live-Übertragung der Messdaten an den Computer
[Bearbeiten]Es ist möglich und je nach Experiment manchmal nötig, die App per Fernzugriff zu steuern. Dazu wird lediglich das Smartphone und ein PC/Tablet benötigt:
- Einrichtung des Smartphones als Hotspot
- Öffnen des Experiments auf der App
- Untermenü öffnen (Button mit den drei vertikal angeordneten Punkten)
- Häkchen bei "Fernzugriff erlauben" setzten und mit "OK" bestätigen
- Verbindung des PCs/ Tablets mit dem Hotspot des Smartphones
- Am PC/Tablet: Internetbrowser öffnen und die auf der App angezeigte URL Adresse eingeben. Das Experiment wird nun auf dem PC angezeigt.
- Das Experiment kann nun am PC/Tablet über den Play-Button gestartet und gestoppt werden.
- Nach dem Versuch können am PC/Tablet im Untermenü unter "Daten exportieren" die gemessenen Daten gespeichert werden und beispielsweise mit Open Office Calc geöffnet und weiterverarbeitet werden. Die Übertragung der Daten ist entweder per Bluetooth oder per Mail möglich
4. Eigenes Experiment erstellen (einfach)
[Bearbeiten]- "Plus-Zeichen" im Hauptmenü drücken
- Namen des Experiments eingeben
- Puffergröße und Sensorrate angeben: 0 steht für die höchstmögliche Genauigkeit
- gewünschter Sensor aktivieren. Wichtig hierbei ist, dass lediglich je ein Sensor benutzt werden kann. Wie die Daten graphisch dargestellt werden, ist nicht wähl- oder veränderbar.
- Experiment speichern, welches anschließend im Hauptmenü aufrufbar ist.
5. Eigenes Experiment erstellen (komplex)
[Bearbeiten]Auf der eigenen PhyPhox-Webseite gibt es einen Editor, in dem komplexere Experimente selbst erstellt werden können. Hier können beispielsweise verschiedene Sensoren miteinander verknüpft werden oder das Design ausgewählt werden. Darüber hinaus kann programmiert werden, welche Daten wie angezeigt bzw. zum Export gespeichert werden. Mit dem Editor eröffnen sich neue Dimensionen an Anwendungsmöglichkeiten zur gezielten Messwerterfassung . So können die Messungen an die didaktischen Vorstellungen des Lehrers und die Voraussetzungen der Klasse individuell angepasst werden.
Erstelltes Experiment teilen und laden:
Im Editor gibt es die Möglichkeit, das erstellte Experiment in einem QR-Code zu speichern. Dieser Code kann als Bild-Datei gespeichert werden und so beispielsweise einer Schulklasse bereitgestellt werden. Der Ablauf ist ganz einfach:
- Öffnen der App auf dem Smartphone
- Im Untermenü auf "Experiment zur Sammlung hinzufügen" drücken
- QR-Code scannen
- Danach kann das Experiment im Hauptmenü gespeichert und benutzt werden
weitere Materialien
[Bearbeiten]Hier finden sich sämtliche Videos und Bilder, die während dieser Arbeit entstanden sind, aber auf der vorliegenden Seite noch nicht verlinkt wurden. Jeder darf diese Dateien - sowie die bisherigen auch - nutzen und weiterverarbeiten, da sie mit einer entsprechenden CC-Lizenz versehen wurden.
https://commons.wikimedia.org/wiki/File:Seilrutsche.webm
https://commons.wikimedia.org/wiki/File:Quickjump.webm
commons.wikimedia.org/wiki/File:Quickjump.webm
- ↑ Dilling, F. & Krause, E. (2020). Zur Authentizität kinematischer Zusammenhänge in der Differentialrechnung - eine Analyse ausgewählter Aufgaben. MNU journal, (2), 163–168. Abgerufen 1. August 2022, von https://www.uni-siegen.de/fb6/didaktik/personen/frederik-dilling/mnu_02-2020_163-168.pdf
