Weltweiter Anstieg der CO2-Emissionen

Modellierungsthema und Zielsetzung

Die Folgen der Erderwärmung sind zur Zeit täglich in den Zeitungen zu lesen: das steigende Erdklima, regionale Wärmerekorde, das Schmelzen der Polkappen, das Steigen der Meeresspiegel, Waldbrände, Ernteverluste der Bauern, Hurrikans und weitere Naturkatastrophen. Um diese Folgen eindämmen zu können, rückt das Zwei-Grad-Ziel immer mehr in den Vordergrund. Beim Klimagipfel von Paris wurde im Jahr 2015 beschlossen, die Erderwärmung auf deutlich unter zwei Grad Celsius im Vergleich zum Beginn der Industrialisierung (etwa 1850n. Chr.) zu begrenzen. Das Ziel ist eine politische Festsetzung, die auf Grundlage wissenschaftlicher Erkenntnisse über die wahrscheinlichen Folgen der globalen Erwärmung erfolgte. Um dieses Ziel noch erreichen zu können, müsste der weltweite Treibhausgas-Ausstoß bis 2050 um bis zu 70% senken und im Jahr 2100 sogar auf 0 senken. Wir wollen uns in unserer Modellierung ansehen, wie CO₂ mit der Erderwärmung zusammenhängt.

Thematische Reduktion

Da die Ursachen der Erderwärmung sehr vielfältig sind und sich gegenseitig beeinflussen, lässt sie sich nicht bloß auf ein Phänomen zurückführen. Einer der wichtigsten Faktoren neben der Massentierhaltung sind hierbei die Treibhausgase, zu denen Kohlenstoffdioxid (CO₂), Methan (CH₄) und Lachgas (N₂O) zählen. "Die Konzentrationen [dieser Gase in unserer Erdatmosphäre] sind als Folge menschlicher Aktivität seit 1750 stark gestiegen". Dieser Anstieg ist in erster Linie durch die Verbrennung fossiler Energieträger (Braunkohle, Steinkohle, Erdgas, Erdöl etc.) zu erklären. Die vom Menschen verursachte Erhöhung der CO₂-Konzentration in unserer Erdatmosphäre um 40% seit der Industrialisierung ist zu 63% Ursache des globalen Klimawandels. Konkret wollen wir uns auf die global stark gestiegenen CO₂-Emissionen bzw. die CO₂-Konzentration der in Erdatmosphäre konzentrieren und beleuchten, in welchem Zusammenhang diese mit der Erderwärmung stehen könnte. Unter Anbetracht des Prozesses der Modellbildung wollen wir uns daher auf die Wirkungen von Treibhausgasen, speziell Kohlenstoffdioxid beschränken, da dieses das am häufigsten von Menschen erzeugte Treibhausgas ist und andere Treibhausgase in deutlich geringeren Mengen emittiert werden. Mit 66% liefert es den mit Abstand größten Beitrag aller klimawirksamen Gase zum Treibhauseffekt (zum Vergleich: Methan 17%, Lachgas 6%). Andere Faktoren, die einen Anstieg des CO₂-Gehalts in der Luft zur Folge haben können, wie z.B. veränderte Sonnenaktivität, Schwankungen der Erdbahn um die Sonne, Vulkanausbrüche, Meteoriteneinschläge oder große Mengen Methans werden bedingt durch den Modellbildungsprozess außer Acht gelassen, da diese die Dimensionen unseres bereits komplexen Projektes sprengen würde.

Fachwissenschaftliche Grundlagen

CO₂

CO₂ ist die chemische Summenformel für das aus Kohlenstoff und Sauerstoffstoff bestehende Molekül Kohlenstoffdioxid. Das Gas Kohlenstoffdioxid ist farblos, gut in Wasser löslich, nicht brennbar, geruchlos und ungiftig. Es ist ein natürlicher Bestandteil der Luft, wobei es mit nur etwa 0,038% einen sehr geringen Teil der Luft ausmacht.
Kohlenstoffdioxid kommt natürlich und in großen Mengen in der Erdatmosphäre vor. Es ist ein natürliches Nebenprodukt der Zellatmung von z.B. Mensch und Tier, entsteht bei der Verbrennung von Holz, Kohle, und Öl, oder wird durch natürliche CO2-Quellen, wie beispielsweise Vulkangase, freigesetzt. Zwar können Pflanzen dieses CO₂ wieder in Sauerstoff, den wir zum Leben brauchen, wieder umwandeln, jedoch wird mittlerweile so viel CO₂ produziert, dass unsere Natur dieses Gas in der großen Menge nicht aufnehmen kann, was zu einem Anstieg der CO₂-Konzentration in unserer Luft führt.

Treibhauseffekt

Doch wie sorgen eigentlich Treibhausgase (im speziellen CO₂) dafür, dass es zu einer globalen Erwärmung der Temperatur kommt? Im Folgenden möchten wir den sogenannten Treibhauseffekt in Kürze erklären.
In den 1830er Jahren hat der französische Physiker Jean-Baptiste Fourier beschrieben, wie Verbrennungsgase die Atmosphäre der Erde aufheizen. Diese sogenannten klimawirksamen Gase sind vor allem Wasserdampf (H₂O), Kohlendioxid (CO₂), Methan (CH₄), Ozon (O₃) und Lachgas (N₂O). Diese Gase kommen schon seit Tausenden von Jahren in unserer Atmosphäre vor und sind natürliche Produkte. Zusätzlich zu dem Aufkommen der natürlichen Treibhausgasen, die essentiell für Leben auf der Erde sind, kommt noch ein anthropogenes (von Menschen geschaffenes) Aufkommen an Treibhausgasen hinzu. Bis zu einem gewissen Grad sind diese Gase lebensnotwendig, denn ohne sie hätten wir eine Durchschnittstemperatur von -18°C auf der Erde. Diese Gase lassen zwar die sehr energiereichen und kurzwelligen Strahlen des Sonnenlichts passieren, aber halten einen Teil der Wärme der von der Erdoberfläche reflektierten, nun langwelligen Strahlen zurück. Ein Gleichgewicht entsteht, durch das sich im Laufe der Jahrtausende unser heutiges lebensfreundlichen Klima einpendeln konnte. (natürlicher Treibhauseffekt)
Bereits leichte Veränderungen der schwachen Treibhausgas-Konzentration bringen unsere Erdatmosphäre aus dem Gleichgewicht. Durch die hohe Menge an anthropogenen Treibhausgasen werden immer mehr langwellige Strahlen nicht mehr durch die Atmosphäre zurück geschickt, sonder nun wieder zur Erde zurück reflektiert. Die kurzwellige Strahlung kann die Atmosphäre und die Treibhausgase zwar noch mühelos passieren, doch die langwelligen Strahlen werden von den Treibhausgasen am Austreten aus der Erdatmosphäre gehindert. Salopp gesagt: die Wärme kommt von außen rein, aber von innen nicht mehr raus. Ein Ungleichgewicht entsteht, das die Erde immer stärker erwärmt. (anthropogener Treibhauseffekt)

Fragestellungen

• Welche Vorhersagen lassen sich über die zukünftige CO2-Emission treffen?
• Welche Vorhersagen lassen sich über die zukünftige CO2-Konzentration treffen?
• Wie wird sich die globale Erderwärmung in den nächsten Jahren entwickeln?
• Wie hängt die steigende CO2-Emission mit der globalen Erderwärmung zusammen?
• Wie hängt die steigende CO2-Konzentration mit der globalen Erderwärmung zusammen?

Studierendengruppe

Moriz Dörr
Eric Schumacher

Zuordnung des Themas zu den SDG

• SDG1: Durch einen reduzierten CO₂-Ausstoß und dem damit verbundenen und angestrebten Ende des Klimawandels werden allgemeine Lebensbedingungen in den Ländern verbessert, in denen der hohe Kohlendioxidausstoß besonders spürbar ist.
• SDG2: Viele Naturkatastrophen wie z.B. Dürren verursachen massive Ernteausfälle. Diese sind teilweise von den extremen CO₂-Emissionen verursacht. Somit ist die Reduzierung des CO₂-Ausstoßes essentiell für das Erreichen des SDG2.
• SDG3: CO₂ ist schädlich für den Menschen. Eine erhöhte Kohlendioxidkonzentration führt zunächst zu Atemdepression und schließlich zu Atemstillstand.
• SDG6: CO₂ trägt erheblich zur weltweiten Luftverschmutzung bei sich auch auf die Trinkwasserqualität auswirkt. Eine Reduzierung der Kohlendioxidemissionen liegt also auch im Interesse sauberen Trinkwassers.
• SDG7: Der Fokus der Energiepolitik sollte auf erneuerbare Energien wie z.B. Wind- und Wasserenergie liegen. Die in die Jahre gekommene und vor allem schädliche Kohleindustrie passt nicht mehr in die heutige Zeit. Somit ist der Kohleausstieg unvermeidlich.
• SDG8: Die Arbeit an erneuerbaren Enegien, die alternative Lösungen hervorbringen, bietet neue Forschungsgebiete.
• SDG12: Es liegt in der Verantowrtung eines jeden Weltbürgers, für das Wohl unserer Erde zu sorgen. Eine zu hohe CO₂-Konzentration in unserer Atmosphäre ist schädlich für unseren Planeten, deren Flora und Fauna, zu der auch wir selbst gehören.
• SDG13: Um den Klimawandel effektiv "zu bekämpfen", wie es beschrieben wird, muss der CO₂-Ausstoß massiv eingedämmt werden. Auch die Forschung auf dem Gebiet der erneuerbaren Energien trägt zur verantowrtungsbewussten Nutzung unserer Ressourcen bei.

Niveaustufen

Welche fachmathematischen Werkzeuge können/sollen für das Modell verwendet werden und auf welchem Niveau (Sek I, Sek II, Uni)?

Sekundarstufe I

• Tabellenkalkulation/ Excel (Datenrecherche/ Datenerhebung in Tabelle/ Diagramme erstellen)
• Geogebra
• funktionaler Zusammenhang erkennen und erläutern
• Funktionsgraph interpretieren können

Sekundarstufe II

• Integralrechnung
• GeoGebra
• Funktion aufstellen

Uniniveau

• anhand der Daten Vermutungen über die Zukunft schließen, Extrapolation
• Formeln erstellen die zur Zielführung beitragen
• Korrelation Korrelation
• Regression

Modellierungszyklen

Zyklus 1

Datenrecherche/Beschaffung der Rohdaten

Unser 1. Zyklus begann mit einer reinen Datenrecherche. Entsprechende Daten fanden wir auf verschiedenen Webseiten, am aussagekräftigsten erachteten wir die Datensätze der NASA.
Wir wollten zunächst einmal verschiedene CO₂-Werte der letzten Jahrzehnte sammeln und ordnen. Sortiert nach den Jahren haben wir nun jeweils die jährliche CO₂-Emission, die CO₂-Konzentration in der Atmosphäre und die globale Temperaturabweichung in einer Tabelle aufgelistet Dabei beschreibt die CO₂-Emission den jährlichen globalen Ausstoß gemessen in Gigatonnen. Die CO₂-Konzentration in der Erdatmosphäre wird in ppm (parts per million, "Anteile pro Million") angegeben. Diese Daten der NASA entstammen dem Mauna Loa Observatory auf Hawaii.

Jahr	CO2-Emission	CO2-Konzentration	globale Temperaturabweichung
2018		409
2017	32,53	407	0,9
2016	32,08	405	0,95
2015	32,294	402	0,86
2014	32.381	399	0,73
2013	32,19	397	0,64
2012	31,49	394	0,61
2011	31,29	392	0,57
2010	29,84	388	0,7
2009	28,32	384	0,63
2008	28,87	383	0,52
2007	28,78	381	0,64
2006	28,003	379	0,62
2005	27,136	377	0,67
2004	26.583	374	0,53
2003	24,983	373	0,61
2002	24,102	371	0,62
2001	23,35	368	0,54
2000	23,01	367	0,4
1999	23,172	365	0,4
1998	22,948	364	0,62
1997	23,035	361	0,42
1996	22,846	360	0,33
1995	22,134	358	0,44
1994	21,92	356	0,31
1993	21,812	354	0,24
1992	21,611	353	0,22
1991	21,57	352	0,41
1990	21,536	532	0,44
1989	21,533	350	0,28
...	...	...	...
1970	14,89	323	0,03
...	...	...	...

CO₂-Werte

Da die obrigen Daten in Tabellenform wenig anschaulich sind, empfahl es sich, diese in Digrammen abzubilden. Abbildung 1 zeigt den zeitlichen Verlauf der globalen CO₂-Emissionen. Die Daten beginnen ab 1970 bis ins Jahre 2018. Deutlich erkennbar ist, dass der Anstieg der weltweiten CO₂-Emissionen auf über das Doppelte des Ausgangswertes im Jahre 1970 steigt und einer deutlichen Steigerung ab dem Jahr 2000. Außerdem kann man eine grobe Linearität erahnen, was uns eventuell Aussagen über die zukünftige Entwicklung schließen lässt.
Das gleiche gilt auch für Abbildung 2, welche den zeitlichen Verlauf der CO₂-Konzentration abbildet. Wir können ablesen, dass die CO₂-Konzentration in der Erdatmosphäre zwischen den Jahren 1973/1974 sowie 1990/1991 stagniert. Tatsächlich aber fand nur ein geringer Anstieg der Konzentration in jenen Jahren statt, der allerdings zu klein für unsere Datenerhebung war. Dies ist auch der Tatsache geschuldet, dass wir die jährlichen Oktoberwerte der Jahre repräsentativ als Jahreswert nahmen und dieser auf eine natürliche Zahl gerundet wurde. Abbildung 2 kann mit der sogenannten Keeling-Kurve verglichen werden (Abb. 3). 1958 gelang dem US-amerikanischen Klimaforscher die graphische Darstellung des mittleren globalen Konzentrationsverlauf von CO₂ und konnte zeigen, dass diese Konzentration durch die Verbrennung fossiler Energieträger zunimmt. Die Abbildung 3 zeigt den typischen schwankenden Jahresverlauf der CO₂-Konzentration der Erdatmosphäre mit einer Abnahme im Frühling und einer Zunahme im Herbst. Dass der Anstieg der CO₂-Emissionen nicht von natürlichen Quellen stammt, erklärt der sogenannte Suess-Effekt: Der österreichische Chemiker Hans Eduard Suess entdeckte, dass der Anteil der Konhelstoff-Isotope in der Luft (¹³C und ¹⁴C) spürbar abnimmt. Da Kohle und Erdöl nur wenig bzw. gar kein ¹³C und ¹⁴C enthalten und weiterhin nur ¹²C bei deren Verbrennung freigesetzt wird, bestätigt seine Entdeckung, dass der Anstieg der Keeling-Kurve von der Verbrennung fossiler Energieträger getrieben wird. Der Klimawandel ist also menschengemacht. Schwankungen der Konzentration von CO₂ in unserer Erdatmosphäre sind in gewissem Maße natürlich. Gründe hierfür sind z.B. Schwankungen der Erdbahn um die Sonne, Vulkanerosionen, Meteoriteneinschläge oder große Mengen Methan. Doch mit keiner dieser genannten Gründe lässt sich der heutige Trend erklären. Daten belegen: die CO₂-Konzentration in der Atmosphäre liegt mindestens so hoch wie seit 800.000 Jahren nicht mehr.

In einem späteren Zyklus werden wir versuchen, Funktionsgleichungen zu den Diagrammen zu finden, die unsere Werte möglichst genau abbilden werden.

• 
  Abb. 1.Verlauf der globalen CO₂-Emissionen
• 
  Abb. 2 Verlauf der globalen CO₂-Konzentration

</gallery>

Temperaturabweichung

Auch die globale Temperaturabweichungen lassen sich gut in einem Diagramm darstellen. Die Abweichungen beschreiben Tempereaturanomalien, d.h. wie viel wärmer bzw. kälter ein Jahr im Vergleich zum mittleren Durchschnitt des 20. Jahrhunderts (1900 bis 1999) war. Diesen Durchschnitt stellt die Null-Grad-Marke im Diagramm dar.
Man kann erkennen, dass ab dem Jahre 1880 fast 100 Jahre lang die Temperaturabweichung permanent unter 0° Celsius liegt. Da in diesem Zeitraum auch die globalen CO₂-Emissionen relativ gering waren, könnte man hier einen ersten Zusammenhang zwischen Temperatur und CO₂-Emissionen feststellen. Hierzu passt auch, dass die globale Temperatur ab den 60er Jahren eine deutliche Steigung durchläuft, also zu der Zeit, ab dem auch die CO2-Emissionen stark gestiegen sind. Ab 1977 befindet sich die Temperaturabweichung kontinuierlich über dem Mittelwert von 0°.
Da wir in unserer Modellierung Prognosen über die zukünftige Temperaturabweichungen treffen wollen, betrachten wir den Zeitraum ab 1970 genauer, da gerade in diesem Abschnitt die Steigerung der Temperaturabweichung gut deutlich wird und wir ab den 70er Jahren lückenlose Daten zu den CO₂-Werten haben.
Mit den Daten ab 1880 können wir unsere Ergebnisse besser in den geschichtlichen Kontext einordnen. Somit können wir ablesen, dass 17 der 18 wärmsten jemals gemessenen Jahre seit 2001 auftraten (die einzige Ausnahme bildet dabei das Jahr 1998). Weiterhin lässt sich beobachten, dass alle 20 wärmsten Jahre seit 1996 auftraten. Beim Blick auf die neuesten Daten fällt außerdem auf, dass die Jahre 2014 bis 2017 die vier wärmsten Jahre, sowie 2016 das absolut wärmste Jahr seit Beginn der Messungen ist.

• 
  Abb. 3 Temperaturabweichung ab 1880
• 
  Abb. 4 Temperaturabweichung ab 1970

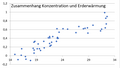
Zusammenhang zwischen CO₂-Konzentration und -Emissionen

Nachdem wir uns die CO₂-Werte bisher nur im zeitlichen Verlauf betrachtet haben, wollen wir nun den Zusammenhang zwischen der CO₂-Konzentration (x-Achse) und der CO₂-Emission (y-Achse) betrachten. Wir haben uns bewusst für diese Rollenverteilung entschieden, da die jährlichen Emissionswerte zu sehr variieren, als dass wir sie als x-Komponente benutzen könnten. Um einen funktionalen Zusammenhang herstellen zu können brauchen wir eine aufsteigende x-Komponente, die uns mit der CO₂-Konzentration gegeben war. Dazu mussten wir lediglich zwei Werte abändern: in den Jahren 1973/1974 sowie 1990/1991 wir jeweils die gleiche Konzentration erreicht (327ppm und 352ppm). Um diese Werte nicht doppelt auf der x-Achse zu haben, nehmen wir das arithmetische Mittel der Jahre, in der der jeweilige Konzentrationswert erreicht wird. Im ersten Fall (1973/1974) ist dies 16,598 Gt, im zweiten Fall 21,618 Gt. Diese Abweichungen kommen zustande, weil wir der Tabelle der Konzentration den aktuellsten Wert (Oktober 2017) genommen haben. Um eine Verzerrung durch den jährlichen Verlauf der durch die Jahreszeiten bedingten CO₂-KOnzentration zu vermeiden, nahmen wir die jährlichen Oktoberwerte als repräsentative Werte für das jeweilige Jahr. Für eine genauere Analyse hätte man das jeweilige arithmetische Mittel der Konzentrationswerte aller 12 Monate des jeweilige Jahres errechnen müssen. Auch hier lässt sich ein annähernd linearer Zusammenhang erahnen, was relativ logisch ist: Wenn mehr CO₂ ausgestoßen wird, steigt auch der CO₂-Anteil in der Luft.

• 
  Abb. 5 Abhängigkeit von Konzentration zu Emission

Zusammenhang zwischen CO₂-Konzentration und Temperaturabweichung

Um unserer Fragestellung "Wie hängen die steigenden CO₂-Emissionen mit der globalen Erderwärmung zusammen?" näher zu kommen, schauen wir uns nun den Zusammenhang zwischen der CO₂-Konzentration (x-Achse) und Temperaturabweichung (y-Achse) vom Jahre 1970 bis heute graphisch an.

• 
  Abb. 6 Zusammenhang zwischen CO2-Konzentration und Temperaturabweichung

Zusammenhang zwischen CO₂-Emissionen und Temperaturabweichung

Um unserer Fragestellung "Wie hängen die steigenden CO₂-Emissionen mit der globalen Erderwärmung zusammen?" näher zu kommen, schauen wir uns nun den Zusammenhang zwischen den CO₂-Emissionen (x-Achse) und Temperaturabweichung (y-Achse) vom Jahre 1970 bis heute graphisch an.

• 
  Abb. 7 Zusammenhang zwischen CO2-Emission und Temperaturabweichung

Zyklus 2

Regressionsanalyse zum Erstellen einer (linearen) Regressionsgleichung

Die Regressionsanalyse ist ein statistisches Verfahren zur Modellierung von Beziehungen zwischen mindestens zwei Variablen (abhängige und unabhängige). Sie wird verwendet, um Zusammenhänge in Daten zu beschreiben und zu analysieren. Des Weiteren lassen sich mit Regressionsanalysen auch Vorhersagen in der Zukunft machen.
Durch die Daten aus dem Zyklus 1 konnten wir mithilfe dieser Regressionsanalyse eine Funktion (Regressiongleichung) erstellen, die Annähernd den zeitlichen, linearen Verlauf beschreibt. So erhalten wir im Folgenden zu allen Grafiken jeweils eine zu den Daten passende Gleichung. Unter der Voraussetzung, dass auch die zukünftigen Werte in ähnlichen Raten wie bisher ansteigt, lassen sich also mithilfe dieser Funktion zukünftige Prognosen treffen.
Den x-Wert nennen wir „Prädiktor“ , die andere Variable y als „Responz“ . Die Festlegung, welches Merkmal Prädiktor und welches Responz ist, hängt ganz vom Sachkontext ab, ist also keine innermathematische Frage

Beispiel: Regressionsgerade der CO₂-Konzentration im zeitlichen Verlauf:

(Abb. Datenwolke)

Wir wollen zur Veranschaulichung der Regressionsanalyse nun die (lineare) Regressionsgerade der CO₂-Konzentration im zeitlichen Verlauf bestimmen. Dabei sollen die Jahreswerte auf der X-Achse, die CO₂-Konzentration auf der Y-Achse abgetragen werden. Der zugrunde liegende Datensatz entnehmen wir aus dem Zyklus 1. Für unser erstes Werte-Paar gibt sich dann folgendes: (x₁ ; d₁) = (1970 ; 323). Unsere Daten werden nun in einer Datenwolke (Abb. rechts) veranschaulicht. Man erkennt das die Daten relativ auf einer Gerade liegen, die durch die Gleichung f(x)=m*x + b beschrieben werden soll, wobei m die Steigung und b den konstanten Teil angibt. Die Abweichungen unsere Punkte zu der Gerade werden als Residuen (r_i mit r_i=d_i - f(x_i)) bezeichnet, welche möglichst klein gehalten werden sollen. Daraus ergibt sich, dass das Minimum ${\sum \limits _{i=1}^{n}|r^{2}|}$ erreicht werden muss. (kleinste Quadraten-Gerade)

Zum Erstellen einer Formel unseres m und b gehen wir nun folgendermaßen vor:

$S(m,b)={\sum \limits _{i=1}^{n}|r^{2}|}$ = ${\sum \limits _{i=1}^{n}|d_{i}-f(x_{i})|^{2}}$ = ${\sum \limits _{i=1}^{n}|d_{i}-(mx_{i}+b)|^{2}}$ = ${\sum \limits _{i=1}^{n}|d_{i}-mx_{i}-b|^{2}}$ OOOOOOO00000OOO(Gleichung *)
mit der Voraussetzung $b={\bar {d}}-m{\bar {x}}$ OOOOoooooooooooooooooooooooooooooooooooooooooOOO........................(Schwerpunkt/ Gleichung **)

Nun setzen wir (**) in (*) ein. Daraus ergibt sich:

$S(m)={\sum \limits _{i=1}^{n}}$$|d_{i}-mx_{i}-{\bar {d}}+m{\bar {x}}|^{2}$ = ${\sum \limits _{i=1}^{n}}$$|(d_{i}-{\bar {d}})-m(x_{i}-{\bar {x}})|^{2}$ = ${\sum \limits _{i=1}^{n}}$$(d_{i}-{\bar {d}})^{2}-2m(d_{i}-{\bar {d}})(x_{i}-{\bar {x}})+(x_{i}-{\bar {x}})^{2}$

Notation:

$Syy={\sum \limits _{i=1}^{n}}$$(d_{i}-{\bar {d}})^{2}$ OOOOOOO00000OOO

$Sxy={\sum \limits _{i=1}^{n}}$$2m(d_{i}-{\bar {d}})(x_{i}-{\bar {x}})$OOOOOOO00000OOO

$Sxx={\sum \limits _{i=1}^{n}}$$(x_{i}-{\bar {x}})^{2}$

Daraus ergibt sich:
$S(m)=Syy-2mSxy+m^{2}Sxx$
$S'(m)=-2Sxy+2mSxx$
Da wir das Minimum suchen muss $S'(m)=0$

$S'(m)=0$ Umgestellt nach m

$=>{\frac {Sxy}{Sxx}}=m$

Für unsere Steigung m ergibt sich final folgende Formel:

$m={\frac {\sum \limits _{i=1}^{n}(d_{i}-{\bar {d}})(x_{i}-{\bar {x}})}{\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}$


Berechnung der Mittelwerte von d (${\bar {d}}$) und x (${\bar {x}}$)

Für ${\bar {d}}$ und ${\bar {x}}$ benutzen wir folgende Formeln: ${\bar {d}}$=${\frac {\sum \limits _{i=1}^{n}d_{i}}{n}}={\frac {d_{1}+d_{2}+...+d_{n}}{n}}$ ${\bar {x}}$=${\frac {\sum \limits _{i=1}^{n}x_{i}}{n}}={\frac {x_{1}+x_{2}+...+x_{n}}{n}}$

OOOOOOO00000OOOOOOOOOOO

Nun setzen wir unsere Werte für di und xi ein. ${\bar {d}}$=${\frac {323+324+...+409}{49}}=359,8367$ ${\bar {x}}$=${\frac {1970+1971+...+2018}{49}}=1994$

Unser Schwerpunkt der Funktion liegt auf unserer gesuchten Gerade $f(x)$ mit den Daten $(1994,359,8367)$mit den Eigenschaften$b=359,8367-m1994$


Berechnung der Steigung m
Zur Berechnung der Steigung m benutzen wir die oben erstellte Formel:

${\frac {\sum \limits _{i=1}^{n}(d_{i}-{\bar {d}})(x_{i}-{\bar {x}})}{\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}={\frac {(d_{1}-{\bar {d}})(x_{1}-{\bar {x}})+(d_{2}-{\bar {d}})(x_{n}-{\bar {x}})+...+(d_{n}-{\bar {d}})(x_{n}-{\bar {x}})}{(x_{1}-{\bar {x}})^{2}+(x_{2}-{\bar {x}})^{2}+...+(x_{n}-{\bar {x}})^{2}}}$

Nun setzen wir unsere Werte für d_i und x_i ein.

${\frac {(323-359,8367)(1970-1994)+(324-359,8367)(1971-1994)+...+(409-359,8367)(2018-1994)}{(1970-1994)^{2}+(1971-1994)^{2}+....+(2018-1994)^{2}}}=1,7614=m$

Für unsere gesichte Funktion $f(x)$ ergibt sich also $m=1,7614$


Berechnung der konstanten b
Als letze Unbekannte wenden wir uns nun. dem Konstanten Teil b zu. Zum Berechnen benutzen wir die oben schon erwähnte Gleichung $b=d-mx$
Durch Einsetzen der bisherigen Ergebnisse ergibt sich:
$b=359,8367-1,7614*1994=-3152,5$


Regressionsgerade
Durch die Ergebnisse ergibt sich folgenden Funkiton der Regressionsgerade:

$f(x)=1,7614*x-3152,5$

Ergebnisse der weiteren Regressionsgeraden
Für die Ergebnisse der weiteren Regressionsgeraden gehen wir analog zu dem obrigen Beispiel vor, jeweils mit den entsprechenden Daten. Daraus ergeben sich folgende Regressionsgeraden:

Regressionsgerade zu CO₂-Emission im zeitlichen Verlauf

$f(x)=0,361x-696$ (Abb. 1.1)

Regressionsgerade zu CO₂-Konzentration im zeitlichen Verlauf

$j(x)=1,761x-3152$ (Abb. 2.1)

Regressionsgerade zu Erderwärmung im zeitlichen Verlauf

$g(x)=0,018x-35,43$ (Abb. 4.1)

Regressionsgerade zu CO₂-Konzentration im Zusammenhang mit der Erderwärmung

$k(x)=0,0104x-3,3434$ (Abb. 6.1)

Regressionsgerade zu CO₂-Emissionn im Zusammenhang mit der Erderwärmung

$l(x)=0,0471x-0,704$ (Abb. 7.1)

• 
  Abb. 1.1.Verlauf der globalen CO2-Emissionen mit Funktionsgleichung
• 
  Abb. 2.1. Verlauf der globalen CO2-Konzentration mit Funktionsgleichung
• 
  Abb. 4.1. Temperaturabweichung ab 1970 mit Funktionsgleichung
• 
  Abb. 6.1 Zusammenhang zwischen CO2-Konzentration und Temperaturabweichung
• 
  7.1 Zusammenhang zwischen CO2-Emission und Temperaturabweichung

Korrelation

Die Korrelation beschreibt den Zusammenhang zwischen mindestens zwei Größen. Der Korrelationskoeffizient gibt den Grad des Zusammenhangs an, welcher mit einem Wert zwischen -1 und 1 angegeben wird. Ist der Wert 0 gibt es keinen Zusammenhang. Die Zahl 1 steht für einen vollständigen positiven linearen Zusammenhang: beide Werte wachsen in gleicher Weise("Je mehr von x, desto mehr von y").
Umgekehrt gibt es auch eine negative Korrelation, die vorliegt, wenn ein Wert wächst, während der andere abnimmt ("je mehr x, desto weniger y")


Beispiel: Berechnung der Korrelation (Korrelationskoeffizient) der CO₂-Konzentration im zeitlichen Verlauf

Wenn man eine Gerade in eine Datenwolke einpasst, ist es oft willkürlich, welche Variable auf die X-Achse und welche auf die Y-Achse abgetragen wird. Für das Ergebnis einer linearen Regression spielt dies aber eine entscheidende Rolle, welches Merkmal als Prädiktor und welches als Responz gewählt wird. Nun vertauschen wir die Rollen von x und y, also wir versuchen, eine Gerade in ein Streudiagramm der Daten $(y_{1},x_{1}),(y_{2},x_{2}),...(y_{n},x_{n})$ hineinzulegen. Analog zu der Regression erhalten wir nun die Gleichung:

$m'={\frac {Sxy}{Syy}}$

mit $f(y)=x={\tilde {m}}x+{\tilde {b}}$

Wenn ${\tilde {m}}={\frac {1}{m'}}$ dann ergibt sich:

${\frac {Sxy}{Syy}}={\frac {Sxx}{Sxy}}$ und durch umstellen erhalten wir:

${\frac {Sxy^{2}}{Sxx*Syy}}=1$


Schließlich nur noch die Wurzel ziehen, dann kommen wir zur Formel für den Korrelationskoeffizienten r:
$r={\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{{\sqrt {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}*{\sqrt {\sum \limits _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}}}$

Wir wollen nun zur Veranschaulichung der Korrelation den Korrelationskoeffizienten r am Beispiel der CO₂-Konzentration im zeitlichen Verlauf berechnen. Dazu benutzen wir die oben erstellte Formel:
$r={\frac {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{{\sqrt {\sum \limits _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}*{\sqrt {\sum \limits _{i=1}^{n}(y_{i}-{\bar {y}})^{2}}}}}$ $={\frac {(x_{1}-{\bar {x}})(y_{1}-{\bar {y}})+(x_{2}-{\bar {x}})(y_{2}-{\bar {y}})+...+(x_{n}-{\bar {x}})(y_{n}-{\bar {y}})}{{\sqrt {(x_{1}-{\bar {x}})^{2}+(x_{2}-{\bar {x}})^{2}+...+(x_{n}-{\bar {x}})^{2}}}*{\sqrt {(y_{1}-{\bar {y}})^{2}+(y_{2}-{\bar {y}})^{2}+...+(y_{n}-{\bar {y}})^{2}}}}}$

Nun setzen wir unsere Werte für $x_{i}$ und $y_{i}$ ein. Daraus ergibt sich:
$r={\frac {(1970-1994)(323-359,8367)+(1971-1994)(324-359,8367)+...+(2018-1994)(409-359,8367)}{{\sqrt {(1970-1994)^{2}+(1971-1994)^{2}+...+(2018-1994)^{2}}}*{\sqrt {(323-359,8367)^{2}+(324-359,8367)^{2}+...+(409-359,8367)^{2}}}}}=0,9920879712$

Was bedeutet das? Der Wert r ist größer als Null, das bedeutet es liegt eine positive Korrelation vor. Da der Wert nah an 1 liegt, spricht man von einer hohen Korrelation, so lässt sich der Wert von Y gut durch den Wert von X vorhersagen.

Korrelation der CO₂-Emission im zeitlichen Verlauf

$r_{1}=0,9733256$
Bedeutung: hohe positive Korrelation

Korrelation der CO₂-Konzentration im zeitlichen Verlauf

$r_{2}=0,99208797$
Bedeutung: hohe positive Korrelation

Korrelation der Erderwärmung im zeitlichen Verlauf

$r_{4}=0,93356804$
Bedeutung: hohe positive Korrelation

Korrelation zwischen CO₂-Konzentration zu Erderwärmung

$r_{6}=0,93652947$
Bedeutung: hohe positive Korrelation

Korrelation zwischen CO₂-Emission zu Erderwärmung

$r_{7}=0,90763916$
Bedeutung: hohe positive Korrelation

Interpretationsfehler

Ein weit verbreiteter Irrtum besteht im Rückschluss von einem hohen Korrelationskoeffizienten (Betrag von r nahe 1) auf kausale Beziehungen zwischen den beiden betrachteten Variablen. Wenn zwei Merkmale X und Y hoch korreliert sind, dann kann es sein, dass das Merkmal X das Merkmal Y verursacht, es kann ebenso gut sein, dass Y die Ursache von X ist. Es kann aber auch vorkommen, dass X und Y eine gemeinsame Ursache Z haben, die für die Korrelation zwischen X und Y verantwortlich ist.
Beispielsweise lässt sich eine hohe Korrelation zwischen der Mathematikleistung von Schülern und ihrer Schuhgröße feststellen. Dies würde ja bedeuten, dass Kinder mit großen Füßen ein besseres mathematische Verständnis haben würden, was eher unwahrscheinlich ist. Beide Variable, Mathematikleistung sowie Schuhgröße, sind stark altersabhängig. Je länger Kinder in die Schule gehen, desto besser können sie mathematische Aufgaben lösen und umso größer sind ihre Füße.
Oft wird übersehen, dass der Korrelationskoeffizient nur die Stärke eines linearen Zusammenhanges misst.

Abb. 3 Temperaturabweichung ab 1880

Zyklus 3

Regressionsanalyse zum Erstellen einer nichtlinearen Regressionsgleichung

Wir versuchen nun für unsere Daten eine noch genauere Regressionsgleichung zu finden, die noch näher an der Wahrheit ist und die die Form einer nichtlinearen Gleichung annimmt. Für kleine Datenmengen oder kurze Zeitintervalle ist eine lineare Funktion eine gute Annäherung, allerdings in vielen Fällen noch nicht ausreichend. Wir schauen uns die Daten zu Temperaturentwicklung im zeitlichen Verlauf ab 1880 an. Die Form der Datenwolke könnte zu einer e-Funktion führen.

Vorgehensweise:

• Transformation der Daten:

Unsere Zielfunktion soll von folgender Gestalt sein: $y=qe^{(}mx)$
Wir brauchen diese Parameter. Diese Gleichung wollen wir transformieren, damit wir eine lineare Gleichung erhalten, mit dieser wir die benötigten Parameter erhalten. Dies geschieht, indem wir den $ln$ bilden. Man erhält:
$log(y)=log(q)+m*x$ (weil $log(e)=1)$ Da unsere Y-Werte zum Teil $<0$ sind, benutzen wir $y*=y+0,5$. Nun sind alle y*-Werte positiv und können den ld davon bilden. Mit diesen $ln(y*)$und $X$-Werten können wir eine lineare Regresionsgleichung bilden. (vgl. Regressionsanalyse oben). Man erhält:$y**=0,0152x-30,508$ $(m*=0,0152$ und $b*=-30,508)$

Analyse/ Prognose

Wir möchten nun versuchen, unsere anfänglichen Fragestellungen zu beantworten:
Dazu brauchen wir noch den Begriff der Extrapolation. Unter Extrapolation wird die Bestimmung eines (oft mathematischen) Verhaltens über den gesicherten Bereich hinaus verstanden (auch als Hochrechnung bezeichnet). Wir können nun mit unseren erstellten Regressionsgeraden, die wir mit Hilfe der Daten $(x_{1},y_{1})....(x_{n},y_{n})$ ermittelt haben, Werte für (x_n+1,y_n+1) bestimmen, also uns an zukünftige Prognosen wagen.

Welche Vorhersagen lassen sich über die zukünftige CO₂-Emission treffen?

Durch die Regressionsanalyse erhielten wir folgende Gleichung:

$f(x)=0,361x-696$

Nun können wir uns für den X-Wert jede beliebige Jahreszahl anschauen, z.B das Jahr 2050 $(x=2050=$.

Setzen wir dafür $x=2050$ in die Gleichung ein. So erhalten wir:

$f(2050)=44,05$

Bedeutet, dass im Jahre 2050 voraussichtlich die globale CO₂-Emission 44,05 Giga-Tonnen beträgt.

Welche Vorhersagen lassen sich über die zukünftige CO₂-Konzentration treffen?

Durch die Regressionsanalyse erhielten wir folgende Gleichung:

$j(x)=1,761x-3152$

Nun können wir für den X-Wert jede beliebige Jahreszahl anschauen, z.B 2050.

Setzen wir dafür $x=2050$ in die Gleichung ein. So erhalten wir:

$j(2050)=458,05$

Bedeutet, dass im Jahre 2050 voraussichtlich die CO₂-Konzentration in unserer Atmosphäre auf 458,05ppm ansteigen wird.

Wie wird sich die globale Erderwärmung in den nächsten Jahren entwickeln?

Durch die Regressionsanalyse erhielten wir folgende Gleichung:

$g(x)=0,018x-35,43$

Nun können wir für den X-Wert jede beliebige Jahreszahl anschauen, z.B 2050.

Setzen wir dafür $x=2050$ in die Gleichung ein. So erhalten wir:

$g(2050)=1,47$

Bedeutet, dass voraussichtlich die globale durchschnittliche Erdtemperatur um 1,47°C gestiegen sein wird.

Zu beginn unseres Projektes haben wir kurz das Zwei-Grad-Ziel thematisiert. Mit unserer Formel können wir nun folgendes berechnen: Wenn wir global weiterhin die Luft so extrem mit CO₂ verschmutzen, in welchem Jahr wird diese Grenze erreicht sein?
$g(x)=2$
$2=0,018x-35,43$ OOOOOOOOO |+35,43

$37,42=0,018x$ OOOOOOOOO |:0,018

$x=2078,88$

Bedeutet, dass wir voraussichtlich Ende 2078 die globale Durchschnittstemperatur um 2°C gestiegen ist und uns somit nur noch 60 Jahre bleiben, bis irreversible Schäden an Natur um Umwelt unvermeidbar sind.

Wie hängt die steigende CO₂-Emission mit der globalen Erderwärmung zusammen?

Durch die Regressionsanalyse erhielten wir folgende Gleichung:

$l(x)=0,0471x-0,704$

Nun können wir für den X-Wert eine zukünftige CO₂-Emission eingeben und erhalten dann den zu erwartenden Wert der globalen Erderwärmung: Z.B 44,05 GT CO₂ $(x=44,05$
So erhalten wir:

$l(44,05)=1,37$

Bedeutet, dass es bei einer CO₂-Konzentration von 458,05 die globale Erderwärmung auf 1,42°C ansteigen wird.

Der Korrelationskoeffizient ergab einen Wert von 0,90763916. Das bedeutet, dass eine hohe positive Korrelation vorliegt. Somit lassen sich sehr gut durch x-Werte Vorhersagen über die y-Werte treffen.

Wie hängt die steigende CO₂-Konzentration mit der globalen Erderwärmung zusammen?

Durch die Regressionsanalyse erhielten wir folgende Gleichung:

$k(x)=0,0104x-3,3434$

Nun können wir für den X-Wert eine zukünftige CO₂-Konzentration einsetzten und erhalten dann den zu erwartenden Wert der globalen Erderwärmung: Z.B eine CO₂-Konzentration von 458,05ppm $(x=458,05)$
So erhalten wir:

$k(458,05)=1,42$

Bedeutet, dass bei einer CO₂-Konzentration von 458,05 die globale Erderwärmung auf 1,42°C ansteigen wird.

Der Korrelationskoeffizient ergab einen Wert von 0,93652947. Das bedeutet, dass eine hohe positive Korrelation vorliegt. Somit lassen sich sehr gut durch x-Werte Vorhersagen über die y-Werte treffen.

Wie wird die globale Erderwärmung im Jahre 2050 aussehen?

Durch unsere Formeln gibt es nun verschiedene Möglichkeiten, die Temperaturabweichung im Jahre 2050 bestimmen zu wollen. Um die Genauigkeit/ Zuverlässigkeit unserer Formeln zu prüfen, wollen wir die Ergebnisse unserer Möglichkeiten miteinander vergleichen (Reliabilität).

* MÖGLICHKEIT 1:
Zunächst geben wir 2050 (Jahreszahl) in $g(x)$ ein (Erderwärmung im zeitlichen Verlauf)
$g(2050)=1,47$
Bedeutet, dass voraussichtlich die globale durchschnittliche Erdtemperatur um 1,47°C gestiegen sein wird.


* MÖGLICHKEIT 2:
Wir schauen uns an, welche CO₂-Emission im Jahre 2050 erwartet wird. Dafür setzen wir 2050 in $f(x)$ ein. Ergibt:
$f(2050)=44,05$
Bedeutet, dass im Jahre 2050 voraussichtlich die globale CO₂-Emission 44,05 Giga-Tonnen beträgt.

Nun setzten wir diesen Emissions-Wert in $l(x)$ (=Zusammenhang CO2-Emission mit globaler Erderwärmung). Ergibt:
$l(44,05)=1,37$
Bedeutet, dass bei einer CO₂-Konzentration von 458,05 im Jahre 205 die globale Erderwärmung auf 1,42°C ansteigen wird.


* MÖGLICHKEIT 3:
Wir schauen uns an, welche CO₂-Konzentration im Jahre 2050 erwartet wird. Dafür setzen wir 2050 in $j(x)$ ein. Ergibt:
$j(2050)=458,05$
Bedeutet, dass im Jahre 2050 voraussichtlich die CO₂-Konzentration in unserer Atmosphäre auf 458,05ppm ansteigen wird.

Nun setzen wir diesen Konzentrations-Wert in $k(x)$ ein. (=Zusammenhang CO2-Konzentration mit globaler Erderwärmung) Ergibt:
$k(458,05)=1,42$
Bedeutet, dass bei einer CO₂-Konzentration von 458,05 die globale Erderwärmung auf 1,42°C ansteigen wird.


Ergebnis: Unsere Ergebnisse für die Temperatur im Jahre 2050 sind relativ nah beieinander, weichen maximal um 0,1°C ab. Bedeutet also, wir kommen bei verschiedenen Wegen immer auf annähernd das gleiche Ergebnis, was für eine hohe Reliabilität spricht.

Interpretation und Reflektion

Wir sind nun am Ende unseres Modellprozesses angekommen. Jetzt geht es darum, die gewonnenen mathematischen Daten zurück in die "reale Welt" zu nehmen. Wir möchten mit unserem Modell zeigen, welche Dringlichkeit die Erderwärmung mit sich führt.

Konkret: anschauliche Annäherung an die Keeling-Kurve Orientierung der weltklimatischen Lage

Natürlich können mithilfe unserer Daten nur wage Prognosen getroffen werden. Selbst der spätere Chemie-Nobelpreisträger Svante Arrhenius prognostizierte im Jahr 1895 nach seinen Erkenntnissen über den Zusammenhang zwischen Verbrennungsgasen und Treibhauseffekt einen Temperaturanstieg von zwei bis sechs Grad Celsius. Abweichungen können z.B. durch die Residuen entstehen. Folgen sind oft erst Jahre, Jahrzehnte oder Jahrhunderte später spür- bzw. messbar. Auch wurde in unserem Modell lediglich der Einfluss des Spurengases CO2 bewertet. Weitere Treibhausgase bzw. Faktoren, die das Klima maßgeblich beeinflussen, übersteigen die Möglichkeiten einer Darstellung im Rahmen dieses Modells und wurden aufgrund ihrer Komplexität vernachlässigt. Diese wurden im Punkt 1.1 Thematische Reduktion erläutert. Allerdings lässt sich mit keiner der natürlichen Ursachen eines Anstiegs des CO₂-Gehalts in der Luft (Sonnenaktivität, Schwankungen der Erdbahn, Vulkanausbrüche Meteoriteneinschläge etc.) der heutige Erwärmungstrend erklären.

Auch lagen die Emissions-Werte in unserer Quelle monatlich dar. Bei knapp 50 Jahren Untersuchungszeitraum, je 12 Monaten wären das extrem viele Daten. Deshalb haben wir pro Jahr nur einen Wert genommen, was u.a die spätere Rechnung vereinfachte. Auch hier könnten jedoch Fehler/ Abweichungen Aufgetreten sein. Um eine genauere Analyse der Konzentration darzustellen, eignet sich die Keeling-Kurve, die einen monatlichen An- bzw. Abstieg darstellt.

Nutzen

Als letztes letztes möchten wir noch anführen, für wen diese Daten nützlich sein könnten:

• Bauern
• Winzer
• Klimaforscher
• Umweltaktivisten
• Politiker
• Lobbyisten
• Unternehmen

Der Anstieg der Erdtemperatur hat schwerwiegende Konsequenzen: wärmeren Meere verursachen heftigere Wirbelstürme, wärmere Luft nimmt mehr Feuchtigkeit auf, was zu stärkeren Regengüssen führt. Stärkere Druckunterschiede verursachen stärkeren Wind. Das Ökosystem der Erde ist hochkomplex und lässt sich leicht aus der Balance bringen. Klimapolitik wird in unserem Zeitalter immer bedeutender. Die Aufklärung dieses hochkomplexen Themas sollte daher schon in der Schule (Primarstufe, Sekundarstufen I und II) geschehen. Unser Modell soll grundlegende Ergebnisse dieses andauernden Prozesses vereinfacht darstellen, sodass ein jeder anhand unserer Sammlungen an Ergebnissen erkennt, von welcher Dringlichkeit eine für unseren Planeten förderliche Klimapolitik ist. Wir erhoffen uns, Menschen die Augen öffnen zu können und sie zu motivieren, etwas gegen den Trend der Erderwärmung zu unternehmen. Lösungsansätze lassen sich dabei sehr leicht finden: jeder kann CO2-Emissionen einsparen, indem er/sie öfters zum Fahrrad greift als jede Strecke mit dem Auto zu erledigen. Auch öffentliche Verkehrsmittel wie Bus oder Bahn sollen hier nicht vergessen werden. Eine Reduzierung des eigenen Plastikverbrauchs liegt ebenfalls in diesem Interesse, da viel Plastik in Müllverbrennungsanlagen vernichtet wird und so den CO2-Ausstoß fördert.

Modellierungsalternativen

Unser Modell hat sich thematisch auf CO₂ und Erderwärmung beschränkt. Jedoch ist nicht nur CO₂ allein Schuld an der Erderwärmung. Man könnte sich in einem alternativen Zyklus z.B anschauen, ob es einen Zusammenhang von Erderwärmung und Bevölkerungsanzahl gibt. Auch sind für den Treibhauseffekt weitere Treibhausgase wie Methan oder Ozon, die wir aufgrund der Komplexität des Themas komplett ignoriert haben, verantwortlich und man könnte sich anschauen, wie diese Gase sich entwickeln bzw. Einfluss auf die Erderwärmung haben.