Kurs:Stochastik/Normalverteilung

Einführung

Die Normal- oder Gauß-Verteilung (nach Carl Friedrich Gauß) ist in der Stochastik ein wichtiger Typ stetiger Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichte wird auch Gauß-Funktion, Gaußsche Normalverteilung, Gaußsche Verteilungskurve, Gauß-Kurve, Gaußsche Glockenkurve, Gaußsche Glockenfunktion, Gauß-Glocke oder schlicht Glockenkurve genannt.

Bedeutung der Normalverteilung

Die besondere Bedeutung der Normalverteilung beruht unter anderem auf dem zentralen Grenzwertsatz, dem zufolge Verteilungen, die durch additive Überlagerung einer großen Zahl von unabhängigen Einflüssen entstehen, unter schwachen Voraussetzungen annähernd normalverteilt sind.

Normalverteilte Abweichung vom Erwartungswert

Die Abweichungen der Messwerte vieler natur-, wirtschafts- und ingenieurwissenschaftlicher Vorgänge vom Erwartungswert lassen sich durch die Normalverteilung (bei biologischen Prozessen oft logarithmische Normalverteilung) entweder exakt oder zumindest in sehr guter Näherung beschreiben (vor allem Prozesse, die in mehreren Faktoren unabhängig voneinander in verschiedene Richtungen wirken).

Beispiele für die Beschreibung zufälliger Vorgänge

Zufallsvariablen mit Normalverteilung benutzt man zur Beschreibung zufälliger Vorgänge wie:

(Messung fehlerhaft) zufällige Messfehler,
(Werkstücke fehlerhaft)zufällige Abweichungen vom Sollmaß bei der Fertigung von Werkstücken,
(Bewegung zufällig) Beschreibung der brownschen Molekularbewegung.

Versicherungsmathematik - Schadensdaten

In der Versicherungsmathematik ist die Normalverteilung geeignet zur Modellierung von Schadensdaten im Bereich mittlerer Schadenshöhen.

Standardabweichung

Die Standardabweichung $\sigma$ beschreibt die Breite der Normalverteilung. Die Halbwertsbreite einer Normalverteilung ist das ungefähr $2{,}4$ -Fache (genau $2{\sqrt {2\ln 2}}$ ) der Standardabweichung.

Verteilung der Messwerte auf Intervalle

Die Verteilung der Messwerte auf Intervalle kann man unter zwei verschiedenen Bezüge zwischen Standardabweichung und prozentualem Anteil der Messwerte angeben:

ausgehend von Vielfachen $n\cdot \sigma$ , Standardabweichung $\sigma >0$ den prozentualen Anteil angeben, den das Intervall $[\mu -n\cdot \sigma ,\mu +n\cdot \sigma ]$
ausgehend von einem prozentualem Anteil der Messwerte, die in einem Intervall $[\mu -\varepsilon \cdot \sigma ,\mu +\varepsilon \cdot \sigma ]$ sind, das zugehörigen $\varepsilon >0$ angeben.

Vielfachen Standardabweichung

Bezogen auf den Verteilungsparameter der Standardabweichung $\sigma >0$ gilt näherungsweise:

Im Intervall der Abweichung $\pm \sigma$ vom Erwartungswert sind 68,27 % aller Messwerte zu finden,
Im Intervall der Abweichung $\pm 2\sigma$ vom Erwartungswert sind 95,45 % aller Messwerte zu finden,
Im Intervall der Abweichung $\pm 3\sigma$ vom Erwartungswert sind 99,73 % aller Messwerte zu finden.

Prozentualer Anteil der Messdaten

Und ebenso lassen sich umgekehrt für gegebene Wahrscheinlichkeiten die maximalen Abweichungen vom Erwartungswert finden:

50 % aller Messwerte haben eine Abweichung von höchstens $0{,}675\sigma$ vom Erwartungswert,
90 % aller Messwerte haben eine Abweichung von höchstens $1{,}645\sigma$ vom Erwartungswert,
95 % aller Messwerte haben eine Abweichung von höchstens $1{,}960\sigma$ vom Erwartungswert,
99 % aller Messwerte haben eine Abweichung von höchstens $2{,}576\sigma$ vom Erwartungswert.

Interpretation Erwartungswert und Standardabweichung

Somit kann neben dem Erwartungswert $\mu$ , der als Schwerpunkt der Verteilung interpretiert werden kann, auch der Standardabweichung eine einfache Bedeutung im Hinblick auf die Größenordnungen der auftretenden Wahrscheinlichkeiten bzw. Häufigkeiten zugeordnet werden.

Definition - Normalverteilung

Eine stetige Zufallsvariable $X$ hat eine (Gauß- oder) Normalverteilung mit Erwartungswert $\mu$ und Varianz $\sigma ^{2}$ ( $-\infty <\mu <\infty ,\sigma ^{2}>0$ ), oft geschrieben als $X\sim {\mathcal {N}}\left(\mu ,\sigma ^{2}\right)$ , wenn $X$ die folgende Wahrscheinlichkeitsdichte hat:^[1]^[2]

f(x\mid \mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\operatorname {exp} \left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)

={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}},-\infty <x<\infty .

Glockenkurve

Der Graph dieser Dichtefunktion hat eine „glockenförmige Gestalt“ und ist symmetrisch mit dem Parameter $\mu$ als Symmetriezentrum, der auch den w:de:ErwartungswertErwartungswert und den Median der Verteilung darstellt. Die Varianz von $X$ ist der Parameter $\sigma ^{2}$ . Weiterhin hat die Wahrscheinlichkeitsdichte Wendepunkte bei $x=\mu \pm \sigma$ .

Numerische Berechnung von Wahrscheinlichkeiten

Die Funktionswert der Verteilungsfunktion über die Dichtefunktion kann numerisch berechnen.

Standardnormalverteilungstabelle

Die Wahrscheinlichkeiten können mithilfe einer Standardnormalverteilungstabelle berechnet werden, die eine Standardform verwendet. Um das zu sehen, benutzt man die Tatsache, dass eine lineare Funktion einer normalverteilten Zufallsvariablen selbst wieder normalverteilt ist.

Lineare Transformation normalverteilter Zufallsvariablen

Konkret heißt das, wenn $X\sim {\mathcal {N}}\left(\mu ,\sigma ^{2}\right)$ und $Y=aX+b$ , wobei $a$ und $b$ Konstanten sind mit $a\neq 0$ , dann gilt $Y\sim {\mathcal {N}}\left(a\mu +b,a^{2}\sigma ^{2}\right)$ . Als Folgerung daraus ergibt sich die Zufallsvariable^[3]

Z={\frac {1}{\sigma }}(X-\mu )\sim {\mathcal {N}}(0,1),

die auch standardnormalverteilte Zufallsvariable $Z$ genannt wird.

Definition - Standardnormalverteilung

Die Standardnormalverteilung ist also die Normalverteilung mit Parametern $\mu =0$ und $\sigma ^{2}=1$ . Die Dichtefunktion der Standardnormalverteilung ist gegeben durch

\varphi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}x^{2}},-\infty <x<\infty .

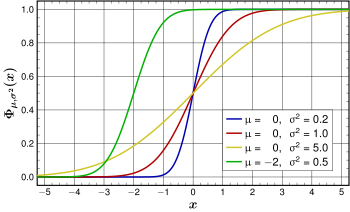
Ihr Verlauf ist nachfolgend graphisch dargestellt.

Graph der Dichtefunktion

Mehrdimensionale Normalverteilung

Die mehrdimensionale Verallgemeinerung ist im Artikel mehrdimensionale Normalverteilung zu finden.

Definition - Verteilungsfunktion

Bei intergrablen Wahrscheinlichkeitsdichten $f:\mathbb {R} \to \mathbb {R} _{o}^{+}$ ist die eindimensionale Verteilungsfunktion wie folgt definiert:

F(x):=\int _{-\infty }^{x}\varphi (t)dt

Graph der Verteilungsfunktion

Eigenschaften

Verteilungsfunktion

Die Verteilungsfunktion der Normalverteilung ist durch

F(x)={\frac {1}{\sigma {\sqrt {2\pi }}}}\int _{-\infty }^{x}e^{-{\frac {1}{2}}\left({\frac {t-\mu }{\sigma }}\right)^{2}}\mathrm {d} t

gegeben. Wenn man durch die Substitution $t=\sigma z+\mu$ statt $t$ eine neue Integrationsvariable $z:={\tfrac {t-\mu }{\sigma }}$ einführt, ergibt sich

F(x)={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{(x-\mu )/\sigma }e^{-{\frac {1}{2}}z^{2}}\mathrm {d} z=\Phi \left({\frac {x-\mu }{\sigma }}\right).

Dabei ist $\Phi$ die Verteilungsfunktion der Standardnormalverteilung

\Phi (x)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{x}e^{-{\frac {1}{2}}t^{2}}\mathrm {d} t.

Symmetrie

Der Graph der Wahrscheinlichkeitsdichte $f\colon \ \mathbb {R} \to \mathbb {R}$ ist eine Gaußsche Glockenkurve, deren Höhe und Breite von $\sigma$ abhängt. Sie ist achsensymmetrisch zur Geraden mit der Gleichung $x=\mu$ und somit eine symmetrische Wahrscheinlichkeitsverteilung um ihren Erwartungswert. Der Graph der Verteilungsfunktion $F$ ist punktsymmetrisch zum Punkt $(\mu ;0{,}5).$ Für $\mu =0$ gilt insbesondere $\varphi (-x)=\varphi (x)$ und $\Phi (-x)=1-\Phi (x)$ für alle $x\in \mathbb {R}$ .

Maximalwert und Wendepunkte der Dichtefunktion

Mit Hilfe der ersten und zweiten Ableitung lassen sich der Maximalwert und die Wendepunkte bestimmen. Die erste Ableitung ist

f'(x)=-{\frac {x-\mu }{\sigma ^{2}}}f(x).

Das Maximum der Dichtefunktion der Normalverteilung liegt demnach bei $x_{\mathrm {max} }=\mu$ und beträgt dort $f_{\mathrm {max} }={\tfrac {1}{\sigma {\sqrt {2\pi }}}}$ .

Die zweite Ableitung lautet

f''(x)={\frac {1}{\sigma ^{2}}}\left({\frac {1}{\sigma ^{2}}}(x-\mu )^{2}-1\right)f(x).

Somit liegen die Wendestellen der Dichtefunktion bei $x=\mu \pm \sigma$ . Die Dichtefunktion hat dort den Wert ${\tfrac {1}{\sigma {\sqrt {2\pi e}}}}$ .

Normierung (1)

Wichtig ist, dass die gesamte Fläche unter der Kurve gleich $1$ , also gleich der Wahrscheinlichkeit des sicheren Ereignisses, ist. Somit folgt, dass, wenn zwei Gaußsche Glockenkurven dasselbe $\mu$ , aber unterschiedliches $\sigma$ haben, die Kurve mit dem größeren $\sigma$ breiter und niedriger ist (da ja beide zugehörigen Flächen jeweils den Wert $1$ haben und nur die Standardabweichung größer ist). Zwei Glockenkurven mit gleichem $\sigma ,$ aber unterschiedlichem $\mu$ haben kongruente Graphen, die um die Differenz der $\mu$ -Werte parallel zur $x$ -Achse gegeneinander verschoben sind.

Normierung (2)

Jede Normalverteilung ist tatsächlich normiert, denn mit Hilfe der linearen Substitution $z={\tfrac {x-\mu }{\sigma }}$ erhalten wir

\int _{-\infty }^{\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}\mathrm {d} x={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }e^{-{\frac {1}{2}}z^{2}}\mathrm {d} z=1.

Für die Normiertheit des letzteren Integrals siehe Fehlerintegral.

Berechnung

Da sich $\Phi (z)$ nicht auf eine elementare Stammfunktion zurückführen lässt, wurde für die Berechnung früher meist auf Tabellen zurückgegriffen (siehe Standardnormalverteilungstabelle). Heutzutage sind in statistischen Programmiersprachen wie zum Beispiel R Funktionen verfügbar, die auch die Transformation auf beliebige $\mu$ und $\sigma$ beherrschen.

Erwartungswert

Der Erwartungswert der Standardnormalverteilung ist $0$ . Es sei $X\sim {\mathcal {N}}\left(0,1\right)$ , so gilt

\operatorname {E} (X)={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{+\infty }x\ e^{-{\frac {1}{2}}x^{2}}\mathrm {d} x=0,

da der Integrand integrierbar und punktsymmetrisch ist.

Ist nun $Y\sim {\mathcal {N}}\left(\mu ,\sigma ^{2}\right)$ , so gilt $X=(Y-\mu )/\sigma$ ist standardnormalverteilt, und somit

\operatorname {E} (Y)=\operatorname {E} (\sigma X+\mu )=\sigma \underbrace {\operatorname {E} (X)} _{=0}+\mu =\mu .

Varianz und weitere Streumaße

Die Varianz der $(\mu ,\sigma ^{2})$ -normalverteilten Zufallsvariablen entspricht dem Parameter $\sigma ^{2}$

\operatorname {Var} (X)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\int _{-\infty }^{\infty }(x-\mu )^{2}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\,\mathrm {d} x=\sigma ^{2}.

Ein elementarer Beweis wird Poisson zugeschrieben.

Standardabweichung der Normalverteilung

Eindimensionale Normalverteilungen werden durch Angabe von Erwartungswert $\mu$ und Varianz $\sigma ^{2}$ vollständig beschrieben. Ist also $X$ eine $\mu$ - $\sigma ^{2}$ -verteilte Zufallsvariable – in Symbolen $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ –, so ist ihre Standardabweichung einfach $\sigma _{X}={\sqrt {\sigma ^{2}}}=\sigma$ .

Streuintervalle (1)

Die Abbildung zeigt Intervalle um $\mu$ bei der Normalverteilung.
Aus der Standardnormalverteilungstabelle ist ersichtlich, dass für normalverteilte Zufallsvariablen jeweils ungefähr

68,3 % der Realisierungen im Intervall

\mu \pm \sigma

,

95,4 % im Intervall

\mu \pm 2\sigma

und

99,7 % im Intervall

\mu \pm 3\sigma

liegen.

Streuintervalle (2)

Da in der Praxis viele Zufallsvariablen annähernd normalverteilt sind, werden diese Werte aus der Normalverteilung oft als Faustformel benutzt. So wird beispielsweise $\sigma$ oft als die halbe Breite des Intervalls angenommen, das die mittleren zwei Drittel der Werte in einer Stichprobe umfasst, siehe Quantil.

Streuintervalle (3)

Die Abbildung zeigt eine Normalverteilung (a) und eine kontaminierte Normalverteilung (b).

Streuintervalle (4)

Diese Praxis ist aber nicht empfehlenswert, denn sie kann zu sehr großen Fehlern führen. Zum Beispiel ist die Verteilung $P=0{,}9\cdot {\mathcal {N}}(\mu ,\sigma ^{2})+0{,}1\cdot {\mathcal {N}}(\mu ,(10\sigma )^{2})$ optisch kaum von der Normalverteilung zu unterscheiden (siehe Bild), aber bei ihr liegen im Intervall $\mu \pm {\overline {\sigma }}$ 92,5 % der Werte, wobei ${\overline {\sigma }}$ die Standardabweichung von $P$ bezeichnet. Solche kontaminierten Normalverteilungen sind in der Praxis sehr häufig; das genannte Beispiel beschreibt die Situation, wenn zehn Präzisionsmaschinen etwas herstellen, aber eine davon schlecht justiert ist und mit zehnmal so hohen Abweichungen wie die anderen neun produziert.

Streuintervalle (5)

Werte außerhalb der zwei- bis dreifachen Standardabweichung werden oft als Ausreißer behandelt. Ausreißer können ein Hinweis auf grobe Fehler der Datenerfassung sein. Andererseits liegt bei einer Normalverteilung im Durchschnitt ca. jeder 20. Messwert außerhalb der zweifachen Standardabweichung und ca. jeder 500. Messwert außerhalb der dreifachen Standardabweichung.

Da der Anteil der Werte außerhalb der sechsfachen Standardabweichung mit ca. 2 ppb verschwindend klein wird, gilt ein solches Intervall als gutes Maß für eine nahezu vollständige Abdeckung aller Werte.

Streuintervalle (6)

Das wird im Qualitätsmanagement durch die Methode Six Sigma genutzt, indem die Prozessanforderungen Toleranzgrenzen von mindestens $6\sigma$ vorschreiben. Allerdings geht man dort von einer langfristigen Erwartungswertverschiebung um 1,5 Standardabweichungen aus, sodass der zulässige Fehleranteil auf 3,4 ppm steigt. Dieser Fehleranteil entspricht einer viereinhalbfachen Standardabweichung ( $4{,}5\ \sigma$ ). Ein weiteres Problem der $6\sigma$ -Methode ist, dass die $6\sigma$ -Punkte praktisch nicht bestimmbar sind. Bei unbekannter Verteilung (d. h., wenn es sich nicht ganz sicher um eine Normalverteilung handelt) grenzen zum Beispiel die Extremwerte von 1.400.000.000 Messungen ein 75-%-Konfidenzintervall für die $6\sigma$ -Punkte ein.^[4]

Streuintervalle (7)

Die Abildung zeigt die Abhängigkeit der Wahrscheinlichkeit (Prozent innerhalb) von der Größe des Streuintervalls $p(z)$ .

Streuintervalle (8)

Die Abbildung zeigt die Abhängigkeit der Streuintervallgrenze von der eingeschlossenen Wahrscheinlichkeit $z(p)$ .

Streuintervalle (9)

Die Wahrscheinlichkeiten $p$ für bestimmte Streuintervalle $[\mu -z\sigma ;\mu +z\sigma ]$ können berechnet werden als

p=2\Phi (z)-1

,

wobei $\Phi (z)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{z}e^{-{\frac {x^{2}}{2}}}\,\mathrm {d} x$ die Verteilungsfunktion der Standardnormalverteilung ist.

Umgekehrt können für gegebenes $p\in (0,1)$ durch

z=\Phi ^{-1}\left({\frac {p+1}{2}}\right)

die Grenzen des zugehörigen Streuintervalls $[\mu -z\sigma ;\mu +z\sigma ]$ mit Wahrscheinlichkeit $p$ berechnet werden.

Ein Beispiel (mit Schwankungsbreite) (1)

Die Körpergröße des Menschen ist näherungsweise normalverteilt. Bei einer Stichprobe von 1.284 Mädchen und 1.063 Jungen zwischen 14 und 18 Jahren wurde bei den Mädchen eine durchschnittliche Körpergröße von 166,3 cm (Standardabweichung 6,39 cm) und bei den Jungen eine durchschnittliche Körpergröße von 176,8 cm (Standardabweichung 7,46 cm) gemessen.^[5]

Ein Beispiel (mit Schwankungsbreite) (2)

Demnach lässt obige Schwankungsbreite erwarten, dass 68,3 % der Mädchen eine Körpergröße im Bereich 166,3 cm ± 6,39 cm und 95,4 % im Bereich 166,3 cm ± 12,78 cm haben,

16 % [ ≈ (100 % − 68,3 %)/2 ] der Mädchen kleiner als 160 cm (und 16 % entsprechend größer als 173 cm) sind und
2,5 % [ ≈ (100 % − 95,4 %)/2 ] der Mädchen kleiner als 154 cm (und 2,5 % entsprechend größer als 179 cm) sind.

Ein Beispiel (mit Schwankungsbreite) (3)

Für die Jungen lässt sich erwarten, dass 68 % eine Körpergröße im Bereich 176,8 cm ± 7,46 cm und 95 % im Bereich 176,8 cm ± 14,92 cm haben,

16 % der Jungen kleiner als 169 cm (und 16 % größer als 184 cm) und
2,5 % der Jungen kleiner als 162 cm (und 2,5 % größer als 192 cm) sind.

Charakteristische Funktion

Die charakteristische Funktion für eine standardnormalverteilte Zufallsvariable $Z\sim {\mathcal {N}}(0,1)$ ist

\varphi _{Z}(t)=e^{-{\frac {1}{2}}t^{2}}.

Für eine Zufallsvariable $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ erhält man daraus mit $X=\sigma Z+\mu$ :

\varphi _{X}(t)=\operatorname {E} (e^{it(\sigma Z+\mu )})=\operatorname {E} (e^{it\sigma Z}e^{it\mu })=e^{it\mu }\operatorname {E} (e^{it\sigma Z})

=e^{it\mu }\varphi _{Z}(\sigma t)=\exp \left\{it\mu -{\tfrac {1}{2}}\sigma ^{2}t^{2}\right\}.

Invarianz gegenüber Faltung (1)

Die Normalverteilung ist invariant gegenüber der Faltung, d. h., die Summe unabhängiger normalverteilter Zufallsvariablen ist wieder normalverteilt (siehe dazu auch unter stabile Verteilungen bzw. unter unendliche teilbare Verteilungen). Eine veranschaulichende Formulierung dieses Sachverhaltes lautet: Die Faltung einer Gaußkurve der Halbwertsbreite $\Gamma _{a}$ mit einer Gaußkurve der Halbwertsbreite $\Gamma _{b}$ ergibt wieder eine Gaußkurve mit der Halbwertsbreite

\Gamma _{c}={\sqrt {\Gamma _{a}^{2}+\Gamma _{b}^{2}}}.

Invarianz gegenüber Faltung (2)

Sind also $X,Y$ zwei unabhängige Zufallsvariablen mit

X\sim {\mathcal {N}}(\mu _{X},\sigma _{X}^{2}),\ Y\sim {\mathcal {N}}(\mu _{Y},\sigma _{Y}^{2}),

so ist deren Summe ebenfalls normalverteilt:

X+Y\sim {\mathcal {N}}(\mu _{X}+\mu _{Y},\sigma _{X}^{2}+\sigma _{Y}^{2})

Das kann beispielsweise mit Hilfe von charakteristischen Funktionen gezeigt werden, indem man verwendet, dass die charakteristische Funktion der Summe das Produkt der charakteristischen Funktionen der Summanden ist (vgl. Faltungssatz der Fouriertransformation).

Invarianz gegenüber Faltung (3)

Gegeben seien allgemeiner $n$ unabhängige und normalverteilte Zufallsvariablen $X_{i}\sim {\mathcal {N}}(\mu _{i},\sigma _{i}^{2})$ .
Dann ist deren Summe wieder normalverteilt

\sum _{i=1}^{n}X_{i}\sim {\mathcal {N}}\left(\sum _{i=1}^{n}\mu _{i},\sum _{i=1}^{n}\sigma _{i}^{2}\right)

und das arithmetische Mittel ebenfalls

{\frac {1}{n}}\sum _{i=1}^{n}X_{i}\sim {\mathcal {N}}\left({\frac {1}{n}}\sum _{i=1}^{n}\mu _{i},{\frac {1}{n^{2}}}\sum _{i=1}^{n}\sigma _{i}^{2}\right).

Nach dem Satz von Cramér gilt sogar die Umkehrung.

Beziehungen zu anderen Verteilungsfunktionen

Transformation zur Standardnormalverteilung (1)

Eine Normalverteilung mit beliebigen $\mu$ und $\sigma$ und der Verteilungsfunktion $F$ hat, wie oben erwähnt, die nachfolgende Beziehung zur ${\mathcal {N}}(0,1)$ -Verteilung:

F(x)=\Phi \left({\tfrac {x-\mu }{\sigma }}\right).

Darin ist $\Phi$ die Verteilungsfunktion der Standardnormalverteilung.

Transformation zur Standardnormalverteilung (2)

Wenn $X\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ , dann führt die Z-Transformation

Z={\frac {X-\mu }{\sigma }}

zu einer standardnormalverteilten Zufallsvariablen $Z$ , denn

P(Z\leq z)=P\left({\tfrac {X-\mu }{\sigma }}\leq z\right)=P\left(X\leq \sigma z+\mu \right)=F(\sigma z+\mu )=\Phi (z).

Geometrisch betrachtet entspricht die durchgeführte Substitution einer flächentreuen Transformation der Glockenkurve von ${\mathcal {N}}(\mu ;\sigma ^{2})$ zur Glockenkurve von ${\mathcal {N}}(0,1)$ .

Approximation der Binomialverteilung durch die Normalverteilung (1)

Die Normalverteilung kann zur Approximation der Binomialverteilung verwendet werden, wenn der Stichprobenumfang hinreichend groß und in der Grundgesamtheit der Anteil der gesuchten Eigenschaft weder zu groß noch zu klein ist (Satz von Moivre-Laplace, zentraler Grenzwertsatz, zur experimentellen Bestätigung siehe auch unter Galtonbrett).

Approximation der Binomialverteilung durch die Normalverteilung (2)

Ist ein Bernoulli-Versuch mit $n$ voneinander unabhängigen Stufen (bzw. Zufallsexperimenten) mit einer Erfolgswahrscheinlichkeit $p$ gegeben, so lässt sich die Wahrscheinlichkeit für $k$ Erfolge allgemein berechnen mittels

P(X=k)={\tbinom {n}{k}}\cdot p^{k}\cdot (1-p)^{n-k},\quad k=0,1,\dotsc ,n.

Diese Binomialverteilung kann durch eine Normalverteilung approximiert werden, wenn $n$ hinreichend groß und $p$ weder zu groß noch zu klein ist. Als Faustregel dafür gilt $np(1-p)\geq 9$ . Für den Erwartungswert $\mu$ und die Standardabweichung $\sigma$ gilt dann:

Approximation der Binomialverteilung durch die Normalverteilung (3)

\mu =n\cdot p

und

\sigma ={\sqrt {n\cdot p\cdot (1-p)}}

.

Damit gilt für die Standardabweichung $\sigma \geq 3$ . Falls diese Bedingung nicht erfüllt sein sollte, ist die Ungenauigkeit der Näherung immer noch vertretbar, wenn gilt: $np\geq 4$ und zugleich $n(1-p)\geq 4$ .

Approximation der Binomialverteilung durch die Normalverteilung (4)

Folgende Näherung ist dann brauchbar:

P(x_{1}\leq X\leq x_{2})=\underbrace {\sum _{k=x_{1}}^{x_{2}}{n \choose k}\cdot p^{k}\cdot (1-p)^{n-k}} _{\mathrm {BV} }

\approx \underbrace {\Phi \left({\frac {x_{2}+0,5-\mu }{\sigma }}\right)-\Phi \left({\frac {x_{1}-0,5-\mu }{\sigma }}\right)} _{\mathrm {NV} }.

Approximation der Binomialverteilung durch die Normalverteilung (5)

Bei der Normalverteilung wird die untere Grenze um 0,5 verkleinert und die obere Grenze um 0,5 vergrößert, um eine bessere Approximation gewährleisten zu können. Dies nennt man auch „Stetigkeitskorrektur“. Nur wenn $\sigma$ einen sehr hohen Wert besitzt, kann auf sie verzichtet werden.

Da die Binomialverteilung diskret ist, muss auf einige Punkte geachtet werden:

Approximation der Binomialverteilung durch die Normalverteilung (6)

Der Unterschied zwischen $<$ oder $\leq$ (sowie zwischen größer und größer gleich) muss beachtet werden (was ja bei der Normalverteilung nicht der Fall ist). Deshalb muss bei $P(X_{\text{BV}}<x)$ die nächstkleinere natürliche Zahl gewählt werden, d. h.

P(X_{\text{BV}}<x)=P(X_{\text{BV}}\leq x-1)

bzw.

P(X_{\text{BV}}>x)=P(X_{\text{BV}}\geq x+1)

,

damit mit der Normalverteilung weitergerechnet werden kann.

Zum Beispiel:

P(X_{\text{BV}}<70)=P(X_{\text{BV}}\leq 69)

Approximation der Binomialverteilung durch die Normalverteilung (7)

Außerdem ist

$P(X_{\text{BV}}\leq x)=P(0\leq X_{\text{BV}}\leq x)$
$P(X_{\text{BV}}\geq x)=P(x\leq X_{\text{BV}}\leq n)$
$P(X_{\text{BV}}=x)=P(x\leq X_{\text{BV}}\leq x)$ (unbedingt mit Stetigkeitskorrektur)

und lässt sich somit durch die oben angegebene Formel berechnen.

Der große Vorteil der Approximation liegt darin, dass sehr viele Stufen einer Binomialverteilung sehr schnell und einfach bestimmt werden können.

Beziehung zur logarithmischen Normalverteilung

Ist die Zufallsvariable $X$ normalverteilt mit ${\mathcal {N}}(\mu ,\sigma ^{2})$ , dann ist die Zufallsvariable $Y=e^{X}$ logarithmisch-normalverteilt, also $Y\sim {\mathcal {LN}}(\mu ,\sigma ^{2})$ .

Die Entstehung einer logarithmischen Normalverteilung ist auf multiplikatives, die einer Normalverteilung auf additives Zusammenwirken vieler Zufallsvariablen zurückführen.

Rechnen mit der Standardnormalverteilung (1)

Bei Aufgabenstellungen, bei denen die Wahrscheinlichkeit für $\mu$ - ${\sigma }^{2}$ -normalverteilte Zufallsvariablen durch die Standardnormalverteilung ermittelt werden soll, ist es nicht nötig, die oben angegebene Transformation jedes Mal durchzurechnen. Stattdessen wird einfach die Transformation

Z={\frac {X-\mu }{\sigma }}

verwendet, um eine ${\mathcal {N}}(0,1)$ -verteilte Zufallsvariable $Z$ zu erzeugen.

Rechnen mit der Standardnormalverteilung (2)

Die Wahrscheinlichkeit für das Ereignis, dass z. B. $X$ im Intervall $[x,y]$ liegt, ist durch folgende Umrechnung gleich einer Wahrscheinlichkeit der Standardnormalverteilung:

${\begin{aligned}P(x\leq X\leq y)&=P\left({\frac {x-\mu }{\sigma }}\leq {\frac {X-\mu }{\sigma }}\leq {\frac {y-\mu }{\sigma }}\right)\\&=P\left({\frac {x-\mu }{\sigma }}\leq Z\leq {\frac {y-\mu }{\sigma }}\right)\\&=\Phi \left({\frac {y-\mu }{\sigma }}\right)-\Phi \left({\frac {x-\mu }{\sigma }}\right)\end{aligned}}$ .

Grundlegende Fragestellungen (1)

Allgemein gibt die Verteilungsfunktion die Fläche unter der Glockenkurve bis zum Wert $x$ an, d. h., es wird das bestimmte Integral von $-\infty$ bis $x$ berechnet. Dies entspricht in Aufgabenstellungen einer gesuchten Wahrscheinlichkeit, bei der die Zufallsvariable $X$ kleiner oder nicht größer als eine bestimmte Zahl $x$ ist. Wegen der Stetigkeit der Normalverteilung macht es keinen Unterschied, ob nun $<$ oder $\leq$ verlangt ist, weil z. B.

P(X=3)=\int _{3}^{3}f(x)\mathrm {d} x=0

und somit

P(X<3)=P(X\leq 3)

.

Analoges gilt für „größer“ und „nicht kleiner“.

Grundlegende Fragestellungen (2)

Dadurch, dass $X$ nur kleiner oder größer als eine Grenze sein (oder innerhalb oder außerhalb zweier Grenzen liegen) kann, ergeben sich für Aufgaben bei Wahrscheinlichkeitsberechnungen zu Normalverteilungen zwei grundlegende Fragestellungen:

Wie groß ist die Wahrscheinlichkeit, dass bei einem Zufallsexperiment die standardnormalverteilte Zufallsvariable $Z$ höchstens den Wert $z$ annimmt?
$P(Z\leq z)=\Phi (z)$

In der Schulmathematik wird für diese Aussage gelegentlich auch die Bezeichnung linker Spitz verwendet, da die Fläche unter der Gaußkurve von links bis zur Grenze verläuft. Für $z$ sind auch negative Werte erlaubt.

Grundlegende Fragestellungen (3)

Allerdings haben viele Tabellen der Standardnormalverteilung nur positive Einträge – wegen der Symmetrie der Kurve und der Negativitätsregel

\Phi (-z)\ =\ 1-\Phi (z)

des „linken Spitzes“ stellt dies aber keine Einschränkung dar.

Grundlegende Fragestellungen (4)

Wie groß ist die Wahrscheinlichkeit, dass bei einem Zufallsexperiment die standardnormalverteilte Zufallsvariable $Z$ mindestens den Wert $z$ annimmt?

P(Z\geq z)=1-\Phi (z)

Hier wird gelegentlich die Bezeichnung rechter Spitz verwendet, mit

P(Z\geq -z)=1-\Phi (-z)=1-(1-\Phi (z))=\Phi (z)

gibt es auch hier eine Negativitätsregel.
Da jede Zufallsvariable $X$ mit der allgemeinen Normalverteilung sich in die Zufallsvariable $Z={\frac {X-\mu }{\sigma }}$ mit der Standardnormalverteilung umwandeln lässt, gelten die Fragestellungen für beide Größen gleichbedeutend.

Streubereich und Antistreubereich (1)

Häufig ist die Wahrscheinlichkeit für einen Streubereich von Interesse, d. h. die Wahrscheinlichkeit, dass die standardnormalverteilte Zufallsvariable $Z$ Werte zwischen $z_{1}$ und $z_{2}$ annimmt:

P(z_{1}\leq Z\leq z_{2})=\Phi (z_{2})-\Phi (z_{1})

Beim Sonderfall des symmetrischen Streubereiches ( $z_{1}=-z_{2}$ , mit $z_{2}>0$ ) gilt:

${\begin{aligned}P(-z\leq Z\leq z)&=P(|Z|\leq z)\\&=\Phi (z)-\Phi (-z)\\&=\Phi (z)-(1-\Phi (z))\\&=2\Phi (z)-1\end{aligned}}$

Streubereich und Antistreubereich (2)

Für den entsprechenden Antistreubereich ergibt sich die Wahrscheinlichkeit, dass die standardnormalverteilte Zufallsvariable $Z$ Werte außerhalb des Bereichs zwischen $z_{1}$ und $z_{2}$ annimmt, zu:

P(Z\leq z_{1}{\text{ oder }}Z\geq z_{2})=\Phi (z_{1})+(1-\Phi (z_{2})).

Somit folgt bei einem symmetrischen Antistreubereich

${\begin{aligned}P(Z\leq -z{\text{ oder }}Z\geq z)&=P(|Z|\geq z)\\&=\Phi (-z)+1-\Phi (z)\\&=1-\Phi (z)+1-\Phi (z)\\&=2-2\Phi (z).\end{aligned}}$

Streubereiche am Beispiel der Qualitätssicherung (1)

Besondere Bedeutung haben beide Streubereiche z. B. bei der Qualitätssicherung von technischen oder wirtschaftlichen Produktionsprozessen. Hier gibt es einzuhaltende Toleranzgrenzen $x_{1}$ und $x_{2}$ , wobei es meist einen größten noch akzeptablen Abstand $\epsilon$ vom Erwartungswert $\mu$ (= dem optimalen Sollwert) gibt. Die Standardabweichung $\sigma$ kann hingegen empirisch aus dem Produktionsprozess gewonnen werden.

Wurde $[x_{1};x_{2}]=[\mu -\epsilon ;\mu +\epsilon ]$ als einzuhaltendes Toleranzintervall angegeben, so liegt (je nach Fragestellung) ein symmetrischer Streu- oder Antistreubereich vor.

Streubereiche am Beispiel der Qualitätssicherung (2)

Im Falle des Streubereiches gilt:

${\begin{aligned}P(x_{1}\leq X\leq x_{2})&=P(|X-\mu |\leq \epsilon )\\&=P(\mu -\epsilon \leq X\leq \mu +\epsilon )\\&=P\left({\frac {-\epsilon }{\sigma }}\leq Z\leq {\frac {\epsilon }{\sigma }}\right)\\&=\Phi \left({\frac {\epsilon }{\sigma }}\right)-\Phi \left({\frac {-\epsilon }{\sigma }}\right)\\&=2\Phi \left({\frac {\epsilon }{\sigma }}\right)-1\\&=\gamma \end{aligned}}$

Der Antistreubereich ergibt sich dann aus $P(|X-\mu |\geq \epsilon )=1-\gamma .\,$

Streubereiche am Beispiel der Qualitätssicherung (3)

Wenn kein Streubereich berechnet wurde durch $P(|X-\mu |\geq \epsilon )=2\cdot \left(1-\Phi \left({\frac {\epsilon }{\sigma }}\right)\right)=\alpha .$

Das Ergebnis $\gamma$ ist also die Wahrscheinlichkeit für verkaufbare Produkte, während $\alpha$ die Wahrscheinlichkeit für Ausschuss bedeutet, wobei beides von den Vorgaben von $\mu$ , $\sigma$ und $\epsilon$ abhängig ist.

Ist bekannt, dass die maximale Abweichung $\epsilon$ symmetrisch um den Erwartungswert liegt, so sind auch Fragestellungen möglich, bei denen die Wahrscheinlichkeit vorgegeben und eine der anderen Größen zu berechnen ist.

Testen auf Normalverteilung (1)

Die Abbildung zeigt die Quantile einer Normalverteilung und einer Chi-Quadrat-Verteilung.

Testen auf Normalverteilung (2)

Eine χ²-verteilte Zufallsvariable mit 5 Freiheitsgraden wird auf Normalverteilung getestet. Für jeden Stichprobenumfang werden 10.000 Stichproben simuliert und anschließend jeweils 5 Anpassungstests zu einem Niveau von 5 % durchgeführt.

Testen auf Normalverteilung (3)

Überprüfungen auf Normalverteilungen sind möglich mittels:

Chi-Quadrat-Test
Kolmogorow-Smirnow-Test
Anderson-Darling-Test (Modifikation des Kolmogorow-Smirnow-Tests)
Lilliefors-Test (Modifikation des Kolmogorow-Smirnow-Tests)
Cramér-von-Mises-Test
Shapiro-Wilk-Test
Jarque-Bera-Test
Q-Q-Plot (deskriptive Überprüfung)
Maximum-Likelihood-Methode (deskriptive Überprüfung)

Testen auf Normalverteilung (4)

Die Tests haben unterschiedliche Eigenschaften hinsichtlich der Art der Abweichungen von der Normalverteilung, die sie erkennen. So erkennt der Kolmogorov-Smirnov-Test Abweichungen in der Mitte der Verteilung eher als Abweichungen an den Rändern, während der Jarque-Bera-Test ziemlich sensibel auf stark abweichende Einzelwerte an den Rändern („heavy tails“) reagiert.

Testen auf Normalverteilung (5)

Beim Lilliefors-Test muss im Gegensatz zum Kolmogorov-Smirnov-Test nicht standardisiert werden, d. h., $\mu$ und $\sigma$ der angenommenen Normalverteilung dürfen unbekannt sein.

Mit Hilfe von Quantil-Quantil-Plots (auch Normal-Quantil-Plots oder kurz Q-Q-Plots) ist eine einfache grafische Überprüfung auf Normalverteilung möglich.
Mit der Maximum-Likelihood-Methode können die Parameter $\mu$ und $\sigma$ der Normalverteilung geschätzt und die empirischen Daten mit der angepassten Normalverteilung grafisch verglichen werden.

Parameterschätzung, Konfidenzintervalle und Tests (1)

Viele der statistischen Fragestellungen, in denen die Normalverteilung vorkommt, sind gut untersucht. Wichtigster Fall ist das sog. Normalverteilungsmodell, in dem man von der Durchführung von $n$ unabhängigen und normalverteilten Versuchen ausgeht. Es existieren drei Fälle:

der Erwartungswert ist unbekannt und die Varianz bekannt
die Varianz ist unbekannt und der Erwartungswert ist bekannt
Erwartungswert und Varianz sind unbekannt.

Parameterschätzung, Konfidenzintervalle und Tests (2)

Je nachdem, welcher dieser Fälle auftritt, ergeben sich verschiedene Schätzfunktionen, Konfidenzbereiche oder Tests. Diese sind detailliert im Hauptartikel Normalverteilungsmodell zusammengefasst.

Dabei kommt den folgenden Schätzfunktionen eine besondere Bedeutung zu:

Parameterschätzung, Konfidenzintervalle und Tests (3)

Das Stichprobenmittel

{\overline {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}

ist ein erwartungstreuer Schätzer für den unbekannten Erwartungswert sowohl für den Fall einer bekannten als auch einer unbekannten Varianz. Er ist sogar der beste erwartungstreue Schätzer, d. h. der Schätzer mit der kleinsten Varianz. Sowohl die Maximum-Likelihood-Methode als auch die Momentenmethode liefern das Stichprobenmittel als Schätzfunktion.

Parameterschätzung, Konfidenzintervalle und Tests (4)

Die unkorrigierte Stichprobenvarianz

V(X)={\frac {1}{n}}\sum _{i=1}^{n}(X_{i}-\mu _{0})^{2}

ist ein erwartungstreuer Schätzer für die unbekannte Varianz bei gegebenem Erwartungswert $\mu _{0}$ . Auch sie kann sowohl aus der Maximum-Likelihood-Methode als auch aus der Momentenmethode gewonnen werden.

Parameterschätzung, Konfidenzintervalle und Tests (5)

Die korrigierte Stichprobenvarianz

V^{*}(X)={\frac {1}{n-1}}\sum _{i=1}^{n}(X_{i}-{\overline {X}})^{2}

ist ein erwartungstreuer Schätzer für die unbekannte Varianz bei unbekanntem Erwartungswert.

Erzeugung normalverteilter Zufallszahlen

Alle folgenden Verfahren erzeugen standardnormalverteilte Zufallszahlen. Durch lineare Transformation lassen sich hieraus beliebige normalverteilte Zufallszahlen erzeugen: Ist die Zufallsvariable $x\sim {\mathcal {N}}(0,1)$ -verteilt, so ist $a\cdot x+b$ schließlich ${\mathcal {N}}(b,a^{2})$ -verteilt.

Box-Muller-Methode

Nach der Box-Muller-Methode lassen sich zwei unabhängige, standardnormalverteilte Zufallsvariablen $X$ und $Y$ aus zwei unabhängigen, gleichverteilten Zufallsvariablen $U_{1},U_{2}\sim U(0,1)$ , sogenannten Standardzufallszahlen, simulieren:

X=\cos(2\pi U_{1}){\sqrt {-2\ln U_{2}}}

und

Y=\sin(2\pi U_{1}){\sqrt {-2\ln U_{2}}}.

Polar-Methode

Die Polar-Methode von George Marsaglia ist auf einem Computer noch schneller, da sie keine Auswertungen von trigonometrischen Funktionen benötigt:

Erzeuge zwei voneinander unabhängige, im Intervall $[-1,1]$ gleichverteilte Zufallszahlen $u_{1}$ und $u_{2}$
Berechne $q=u_{1}^{2}+u_{2}^{2}$ . Falls $q=0$ oder $q\geq 1$ , gehe zurück zu Schritt 1.
Berechne $p={\sqrt {\frac {-2\cdot \ln q}{q}}}$ .
$x_{i}=u_{i}\cdot p$ für $i=1,2$ liefert zwei voneinander unabhängige, standardnormalverteilte Zufallszahlen $x_{1}$ und $x_{2}$ .

Zwölferregel (1)

Der zentrale Grenzwertsatz besagt, dass sich unter bestimmten Voraussetzungen die Verteilung der Summe unabhängig, identisch verteilter Zufallszahlen einer Normalverteilung nähert.

Ein Spezialfall ist die Zwölferregel, die sich auf die Summe von zwölf Zufallszahlen aus einer Gleichverteilung auf dem Intervall [0,1] beschränkt und bereits zu passablen Verteilungen führt.

Zwölferregel (2)

Allerdings ist die geforderte Unabhängigkeit der zwölf Zufallsvariablen $X_{i}$ bei den immer noch häufig verwendeten Linearen Kongruenzgeneratoren (LKG) nicht garantiert. Im Gegenteil wird vom Spektraltest für LKG meist nur die Unabhängigkeit von maximal vier bis sieben der $X_{i}$ garantiert. Für numerische Simulationen ist die Zwölferregel daher sehr bedenklich und sollte, wenn überhaupt, dann ausschließlich mit aufwändigeren, aber besseren Pseudo-Zufallsgeneratoren wie z. B. dem Mersenne-Twister (Standard in Python, GNU R) oder WELL genutzt werden. Andere, sogar leichter zu programmierende Verfahren, sind daher i. d. R. der Zwölferregel vorzuziehen.

Verwerfungsmethode

Normalverteilungen lassen sich mit der Verwerfungsmethode (siehe dort) simulieren.

Anwendungen außerhalb der Wahrscheinlichkeitsrechnung

Die Normalverteilung lässt sich auch zur Beschreibung nicht direkt stochastischer Sachverhalte verwenden, etwa in der Physik für das Amplitudenprofil der Gauß-Strahlen und andere Verteilungsprofile.

Zudem findet sie Verwendung in der Gabor-Transformation.

Siehe auch

Literatur

Stephen M. Stigler: The history of statistics: the measurement of uncertainty before 1900. Belknap Series. Harvard University Press, 1986. ISBN 9780674403413.

Weblinks

Commons: Normalverteilung – Sammlung von Bildern, Videos und Audiodateien

Wikibooks: Anschauliche Darstellung der Normalverteilung – Lern- und Lehrmaterialien

Einzelnachweise

↑ Bei $e^{x}$ handelt es sich um die Exponentialfunktion mit der Basis $e.$
↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. 1988, S. 47.
↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. 1988, S. 48.
↑ H. Schmid, A. Huber: Measuring a Small Number of Samples and the 3σ Fallacy. (PDF) In: IEEE Solid-State Circuits Magazine. Bd. 6, Nr. 2, 2014, S. 52–58, doi:10.1109/MSSC.2014.2313714.
↑ Mareke Arends: Epidemiologie bulimischer Symptomatik unter 10-Klässlern in der Stadt Halle. Dissertation. Martin-Luther-Universität Halle-Wittenberg, 2005, Tabelle 9, S. 30.

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Stochastik' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Stochastik/Normalverteilung
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

Wikipedia2Wikiversity

Diese Seite wurde auf Basis der folgenden Wikipedia-Quelle erstellt:

[1] Bei $e^{x}$ handelt es sich um die Exponentialfunktion mit der Basis $e.$

[2] George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. 1988, S. 47.

[3] George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl, T. C. Lee: Introduction to the Theory and Practice of Econometrics. 1988, S. 48.

[4] H. Schmid, A. Huber: Measuring a Small Number of Samples and the 3σ Fallacy. (PDF) In: IEEE Solid-State Circuits Magazine. Bd. 6, Nr. 2, 2014, S. 52–58, doi:10.1109/MSSC.2014.2313714.

[5] Mareke Arends: Epidemiologie bulimischer Symptomatik unter 10-Klässlern in der Stadt Halle. Dissertation. Martin-Luther-Universität Halle-Wittenberg, 2005, Tabelle 9, S. 30.

[1]

[2]

[3]

[4]

[5]