Kurs:Topologische Invertierbarkeitskriterien/B-Regularität

Einführung

Wenn wir die ${\mathcal {B}}$ -Regularität eines Elementes $z\in A$ für eine topologische Algebra $(A,{\mathcal {T}}_{A})$ sprechen, suchen wir nach einer Algebraerweiterungen $(B,{\mathcal {T}}_{B})$ von $(A,{\mathcal {T}}_{A})$ in der $z\in A$ invertierbar ist und sowohl $(A,{\mathcal {T}}_{A})$ als auch $(B,{\mathcal {T}}_{B})$ Banachalgebren sind. Dabei reicht es zu zeigen, dass eine normierte Algebraerweiterung $(B_{0},{\mathcal {T}}_{B_{0}})$ existiert, in der $z\in A$ invertierbar ist. Ist $(B_{0},{\mathcal {T}}_{B_{0}})$ dann nicht vollständig, vervollständigt man ggf. die Algebraerweiterung $B_{0}$ dann zu $B$ mit $z\in B_{0}\subseteq B$ . Wenn $z\in A$ in $B_{0}$ ein inverses Element $b$ besitzt, besitzt $z\in A$ auch in der Vervollständigung $B\supseteq B_{0}$ ein inverses Element.

Zielsetzung

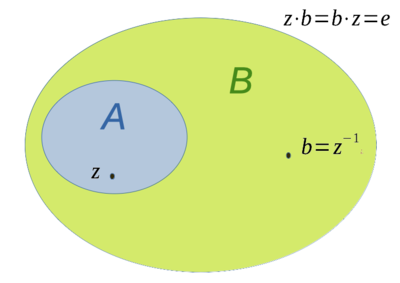
Zielsetzung einer Banachalgebraerweiterung $(B,\|\cdot \|_{B})$ zu einer gegebenen topologischen Algebra $(A,\|\cdot \|_{A})$ mit $z\in A$ ist es, die gegebene Banachalgebra so zu vergrößern, dass diese ein inverses Element $z^{-1}:=b\in B$ in der Banachalgebra $B$ enthält. Für kommutative Banachalgebren erhält man folgende Charakterisierung^[1]:

$z\in A$ permanent singulär $\Longleftrightarrow$ $z\in {\mathcal {TNT}}(A)$ (topologischer Nullteiler)
$z\in A$ ${\mathcal {B}}$ -regulär $\Longleftrightarrow$ es gibt ein $D>0$ mit $\|x\|\leq D\cdot \|z\cdot x\|$ für alle $x\in A$

Veranschaulichung

Algebraerweiterung $B$ von $A$ ist hier wieder eine Banachalgebra, die ein inverses Element $b=z^{-1}\in B$ zu einem gegebenen $z\in A$ enthält.

Vollständigkeit

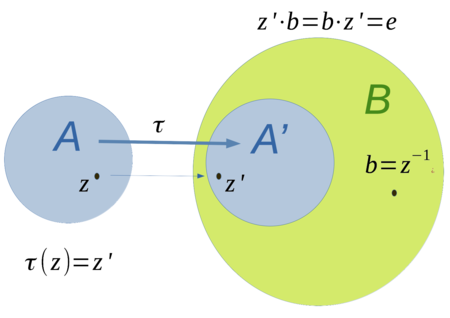
Zunächst einmal betrachtet man normierte Algebraerweiterungen $(B_{0},\|\cdot \|_{B_{0}})$ von $(A,\|\cdot \|_{A})$ , in denen man ein inverses Element $b=z^{-1}\in B_{0}$ zu der gegebenen $z\in A$ enthält. Wenn man in der normierten Algebraerweiterung ein inverses Element $z^{-1}\in B_{0}$ zu $z\in A$ gefundet hat, vervollständigt man $(B_{0},\|\cdot \|_{B_{0}})$ zu einer Banachalgebra $(B,\|\cdot \|_{B})$ mit $b=z^{-1}\in B_{0}\subseteq B$ (siehe Vollständigkeit)

Algebraerweiterung - Zahlbereichserweiterung

In dem folgenden Folien wird Verwendung der Vollständigkeit in der Funktionalanalysis in Bezug zur Zahlbereichserweiterungen im Kontext der Schule kurz behandelt.

Cauchyfolgen in der Sekundarstufe

Jede irrationale Zahl $x\in \mathbb {R} \setminus \mathbb {Q}$ kann man Cauchy-Folge in $\mathbb {Q}$ darstellen.

1,4142\ldots ={\sqrt {2}}=\lim _{n\to \infty }a_{n}

mit

a_{1}=1,\,a_{2}={\frac {14}{10}},\,a_{3}={\frac {141}{100}},\,a_{4}={\frac {1414}{1000}},\,a_{4}={\frac {14142}{10000}},\ldots

.

Rationale Zahlen und Normen

In den rationalen Zahlen ist der Betrag $|\cdot |_{\mathbb {Q} }$ die Norm, die den Raum $(\mathbb {Q} ,|\cdot |_{\mathbb {Q} })$ aus funktionalanalytischer Sicht zu einer eindimensionalen topologischen Algebra über dem Körper $\mathbb {K} :=\mathbb {Q}$ macht. Mit $d(x,y):=|x-y|_{\mathbb {Q} }$ kann man $\mathbb {Q}$ auch als einen metrischen Raum auffassen und diese Algebra über Äquivalenzklassenbildung von Cauchy-Folgen zu den reellen Zahlen $\mathbb {R}$ vervollständigen.

Inverse in Vervollständigungen

Wenn $b=z^{-1}={\frac {1}{5}}$ das inverse Element zu $5$ in $B_{0}:=\mathbb {Q}$ ist, bleibt es das inverse Element in der Algebraerweiterung von $(\mathbb {R} ,|\cdot |_{\mathbb {R} })$ , wobei $|\cdot |_{\mathbb {R} }$ der Betragsfunktion in den reellen Zahlen $\mathbb {B} =\mathbb {R} \supset \mathbb {Q} =B_{0}$ ist.

Definition:

Sei ${\textstyle {\mathcal {Kc}}_{e}}$ eine Klasse von unitalen Algebren und ${\textstyle A\in {\mathcal {K}}_{e}}$ , dann heißt ${\textstyle B\in {\mathcal {K}}_{e}}$ Algebraerweiterung, Oberalgebra oder ${\textstyle {\mathcal {K}}}$ -Erweiterung von ${\textstyle A}$ , falls es einen Algebraisomorphismus ${\textstyle \tau :A\longrightarrow A'\subset B}$ gibt mit:

${\textstyle \tau (e_{_{A}})=e_{_{B}}}$ , wobei ${\textstyle e_{_{A}}}$ ist das Einselement von ${\textstyle A}$ und ${\textstyle e_{_{B}}\in A'}$ das Einselement von ${\textstyle B}$ ist.
${\textstyle A}$ ist homöomorph zu ${\textstyle A'}$ ; d.h. ${\textstyle \tau }$ und ${\textstyle \tau ^{-1}:A'\longrightarrow A}$ sind stetig.

Veranschaulichung - Algebraisomorphismus

Bemerkung

Im allgemeinen identifiziert man ${\textstyle A}$ mit ${\textstyle A'}$ und schreibt ${\textstyle A\subset B}$ .
Sei ${\textstyle {\mathfrak {U}}_{A'}(0)}$ eine Nullumgebungsbasis der Relativtopologie von ${\textstyle B}$ auf ${\textstyle A'}$ und ${\textstyle {\mathfrak {U}}_{A}(0)}$ eine Nullumgebungsbasis von ${\textstyle A}$ , dann kann man die Homöomorphie zwischen ${\textstyle A}$ und ${\textstyle A'}$ wie immer über die Topologie ausdrückeen:

{\begin{array}{rcl}\forall _{\displaystyle V\in {\mathfrak {U}}_{A}(0)}\exists _{\displaystyle U\in {\mathfrak {U}}_{A'}(0)}&:&U\subset V\,\,\,(\tau (U)\subset V)\\\forall _{\displaystyle U\in {\mathfrak {U}}_{A'}(0)}\exists _{\displaystyle V\in {\mathfrak {U}}_{A}(0)}&:&V\subset U\,\,\,(\tau ^{-1}(V)\subset U).\end{array}}

Stetigkeit und Norm

Betrachtet man die Normen ${\textstyle \left\|\cdot \right\|_{A'}}$ und ${\textstyle \left\|\cdot \right\|_{A}}$ für Nullumgebungen, so lassen sich die oberen beiden Aussagen wie folgt umformulieren (siehe auch Stetigkeitssatz für lineare Abbildungen):

{\begin{array}{rcl}\exists _{\displaystyle C_{1}>0}\forall _{x\in A}&:&\left\|x\right\|_{A}\leq C_{1}\cdot \left\|\tau (x)\right\|_{A'}\\{\mbox{ bzw. }}&&\left\|\cdot \right\|_{A}\leq C_{1}\cdot \left\|\cdot \right\|_{A'}\circ \tau \\\exists _{\displaystyle C_{2}>0}\forall _{x\in A}&:&\left\|\tau (x)\right\|_{A'}\leq C_{2}\cdot \left\|x\right\|_{A}\\{\mbox{ bzw. }}&&\left\|\cdot \right\|_{A'}\circ \tau \leq C_{2}\cdot \left\|\cdot \right\|_{A}.\end{array}}

Konstruktion Algebraisomorphismus

Für die Konstruktion des Algebraisomorphismus geht man wie folgt vor:

(KA1) man konstruiert zunächst eine Algebrahomomorphismus $\tau :A\to B$ und zeigt, dass dieser stetig ist.
(KA2) man zeigt, dass der Algebrahomomorphismus injektiv ist $Kern(\tau )=\{0_{A}\}$
(KA3) man definiert mit $A':=\tau (A)\subset B$ , die Umkehrabbildung $\tau ^{-1}:A'\to A$ und zeigt, dass $\tau ^{-1}$ ebenfalls stetig ist (siehe Stetigkeitssatz für lineare Abbildungen).

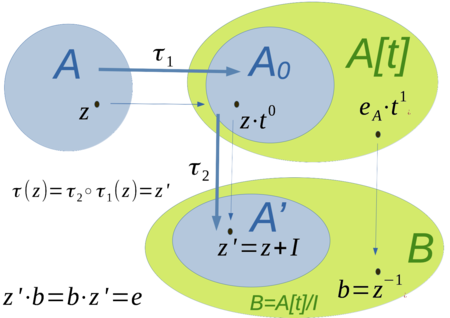
Normierte Polynomalgebra

Wir betrachten nun zu einer gegeben Banachalgebra ${\textstyle \left(A,\left\|\cdot \right\|_{A}\right)\in {\mathcal {B}}(\mathbb {K} )}$ die Menge der Polynome mit Koeffizienten in $A$ .

p(t)=\sum _{k=0}^{n}p_{k}\cdot t^{k}{\mbox{ mit }}p_{k}\in A{\mbox{ für }}k\in \{0,1,...,n\}

und Potenzreihen mit Koeffizienten in der Algebra $A$

p(t)=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ mit }}p_{k}\in A{\mbox{ für }}k\in \mathbb {N} _{o}

Bemerkung: Polynomalgebren

Bei der Konstruktion der Algebraerweiterung, in der ein $z\in A$ invertierbar ist, wird in einem ersten Schritt die Algebra der Polynome $A[t]$ betrachtet. Die folgende Abbildung zeigt, wie die Algebraerweiterung $B$ über die Polynomalgebra konstruiert wird.

Grad von Polynomen

Zunächst einmal würde man Polynome formal eher in der obigen Form mit $n\in \mathbb {N} _{o}$ notieren und mit $p_{n}\not =0_{A}$ würde $n$ den Grad des Polynoms angeben. Für das Cauchyprodukt von zwei Polynomen $p,q\in A[t]$ ist diese Schreibweise allerdings ungeeignet, da bei der Addition und Multiplikation zwei Polynomen $p,q\in A[t]$ die Handhabung des Grades zusätzlichen formalen Aufwand nach sich zieht, der aber für die weitern Betrachtungen von Algebraerweiterungen keine Rolle spielt.

Schreibweise für die Polynomalgebra

Daher werden die Polynome wie folgt über "endliche" Folgen $c_{oo}(A)$ definiert, die ab einer Indexschranke $n\in \mathbb {N} _{o}$ nur noch aus dem Nullvektor $0_{A}$ in $A$ besteht.

p(t)=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ mit }}(p_{k})_{k\in \mathbb {N} _{0}}\in c_{oo}(A)

Topologisierung der Polynomalgebra

Für die Normdefinition von Polynomen $p\in A[t]$ wird nun eine Folge $(C_{k})_{k\in \mathbb {N} }$ von positiven Konstanten in $\mathbb {R} ^{+}$ verwendet um $A[t]$ zu topologisieren.

\|\!|p|\!\|:=\displaystyle \sum _{k=0}^{\infty }C_{k}\cdot \|p_{k}\|_{A}{\mbox{ mit }}(p_{k})_{k\in \mathbb {N} _{0}}\in c_{oo}(A)

Definition der Koeffizientenfolge für die Norm

Für eine gegebene feste positive Konstante $D>0$ setzt man $C_{k}:=D^{k}$ und kann man die Koeffizientenfolge $(D^{k})_{k\in \mathbb {N} }$ wie folgt für die Normdefinition verwenden:

\|\!|p|\!\|_{D}\displaystyle :=\sum _{k=0}^{\infty }D^{k}\cdot \|p_{k}\|_{A}{\mbox{ mit }}(p_{k})_{k\in \mathbb {N} _{0}}\in c_{oo}(A)

Cauchy-Produkt - Stetigkeit

Betrachtet man zwei Polynome $p,q\in A[t]$ in dem normierten Raum $(A[t],\|\!|\cdot |\!\|_{D})$ .

p(t):=\sum _{k=0}^{\infty }p_{k}\cdot t^{k}{\mbox{ und }}q(t):=\sum _{k=0}^{\infty }q_{k}\cdot t^{k}

Dann liefert die Definition der Norm für das Produkt $p\cdot q$ :

\|\!|p\cdot q|\!\|_{D}=\displaystyle \sum _{n=0}^{\infty }D^{n}\cdot \left\|\sum _{k=0}^{n}p_{k}\cdot q_{n-k}\right\|_{A}

Aufgabe für die Lernende

Beweisen Sie, dass die folgende Abbildung $\|\!|\cdot |\!\|_{D}:\to \mathbb {R} ^{+}$ eine Norm ist und für alle $p,q\in A[t]$ gilt

\|\!|p\cdot q|\!\|_{D}\leq \|\!|p|\!\|_{D}\cdot \|\!|q|\!\|_{D}

D.h., dass die Multiplikation auf $(A[t],\|\!|\cdot |\!\|_{D})$ stetig ist. Der Index $D\in \mathbb {R} ^{+}$ bezeichnet die gewählte Basis für die Koeffizienten $D^{n}$ .

Ideale in Polynomalgebren

Wenn $z\in A$ kein topologischer Nullteiler ist und man $D>0$ für Abschätzung bzgl. der Norm erhält, dann topologisiert man mit diesem $D$ die Polynomalgebra und erzeugt bzgl. des Polynoms $p(t):=z\cdot t-e_{A}$ ein topologisch abgeschlossenes Hauptideal $I\subset A[t]$ . Diese Topologisierung der Algebraerweiterung erfolgt über den Quotientenraum $B:=A[t]/I$ des Ideals $I$ in $A[t]$ .

Topologische Eigenschaft von z

In der Algebra $A$ sei $z\in A$ kein topologischer Nullteiler, dann gibt es ein $D>0$ mit:

\forall _{x\in A}:\,\,\|x\|_{A}\leq D\cdot \|z\cdot x\|_{A}\,\,\wedge \,\,\|x\|_{A}\leq D\cdot \|x\cdot z\|_{A}

Ohne Einschränkung sei $D\geq 1$ . Im Falle von $D<1$ gilt die Ungleichung

\forall _{x\in A}:\,\,\|x\|_{A}\leq \|z\cdot x\|_{A}\,\,\wedge \,\,\|x\|_{A}\leq \|x\cdot z\|_{A}

und man kann $D=1$ wählen.

Ideale in der Polynomalgebra

Für dieses $z\in A$ definiert man ein Polynom $o\in A[t]$ mit $o(t):=z\cdot t-e_{A}$ , wobei $e_{A}$ das Einselement der Multiplikation in $A$ ist.

Zweiseitiges Hauptideal

Man definiert nun ein zweiseitiges Hauptideal in $A[t]$ bzgl. eines Polynoms $p\in A[t]$ mit $o(t):=z\cdot t-e_{A}$ über

I_{z}:={\mathfrak {E}}(p)=\{q^{(1)}+\dotsb +q^{(n)}\mid n\in \mathbb {N} {\mbox{ und }}q^{(k)}\in A[t]\cdot o\cdot A[t]\}.

Das gesuchte Ideal $I:={\overline {I_{z}}}\subset A[t]$ ist nun der topologische Abschluss in der Polynomalgebra $A[t]$ bzgl. der Norm $\|\!|\cdot |\!\|_{D}$ auf $A[t]$ .

Hauptideal in kommutativen Algebren

In einer kommutativen Algebra $A$ besteht das zweiseitige Hauptideal in $A[t]$ bzgl. eines Polynoms $p\in A[t]$ mit $o(t):=z\cdot t-e_{A}$ aus Polynomen $r\in I_{z}:={\mathfrak {E}}(o)=o\cdot A[t]$ der folgenden Form:

{\begin{array}{rcl}r(t)&=&\displaystyle \sum _{k=0}^{\infty }r_{k}\cdot t^{k}\\&{\mbox{mit}}&r\in p\cdot A[t]\\\exists _{q\in A[t]}:\,\,\,r_{0}=-q_{0}&\wedge &\left(\forall _{k>0}:r_{k}=z\cdot q_{k-1}+q_{k}\right)\end{array}}

Aufgaben für Lernende

Sei nun die Algebra $A$ nicht kommutativ bzgl. der Multiplikation. Bestimmen Sie nun für das zweiseitige Hauptideal $I_{z}:={\mathfrak {E}}(p)$ in $A[t]$ bzgl. des Polynoms $o\in A[t]$ mit $o(t):=z\cdot t-e_{A}$ die Koeffizienten von Polynomen $r\in I_{z}:={\mathfrak {E}}(o)$ mit:

{\begin{array}{rcl}r(t)&=&\displaystyle \sum _{k=0}^{\infty }r_{k}\cdot t^{k}\\&{\mbox{mit}}&q^{(1)},q^{(2)}\in A[t]:r=q^{(1)}\cdot p\cdot q^{(2)}{\mbox{ und }}\\q^{(i)}&=&\displaystyle \sum _{k=0}^{\infty }q_{k}^{(i)}\cdot t^{k},\,\,\,\,\,\,i\in \{1,2\}\\\end{array}}

Algebraerweiterung

Der Algebrahomomorphismus $\tau :A\to B$ bildet nun jedes Element $x\in A$ auf die Nebenklasse $x+I\in B:=A[t]/I$ ab.

Abgeschlossenes Hauptideal in der Polynomalgebra

Für das gegebene $z\in A$ in der kommutativen normierten topologische Algebren $(A,\|\cdot \|_{A})$ definiert man ein Polynom $o\in A[t]$ mit $o(t):=z\cdot t-e_{A}$ , wobei $e_{A}$ das Einselement der Multiplikation in $A$ ist. Als Ideal definiert man $I:={\overline {o\cdot A[t]}}$ als abgeschlossenes Hauptideal in $A[t]$ . Als Untervektorraum $I$ wäre der Quotientenraum auch ein Vektorraum. Die zusätzliche Eigenschaft des Ideals sorgt dafür, dass auch die Multiplikation auf dem Quotientenraum wohldefiniert ist.

Aufgabe für Lernende

Betrachten Sie eine kommutative Algebra $A\in {\mathcal {B}}_{e}^{k}(\mathbb {K} )$ über dem Körper $\mathbb {K}$ .

Zeigen Sie, dass mit der Abbildung $\tau :A\to B$ und $\tau (x)=x_{_{I}}=x+I$ eine Algebraerweiterung von $A$ nach $B$ definiert wurde!
Zeigen Sie, dass $e_{_{B}}:=e_{_{A}}+I$ das neutrale Element der Multiplikation in $B$ ist.
Zeigen Sie, dass $z\in A$ in $B$ invertierbar ist mit $b_{_{I}}=b+I$ und $b(t):=e_{A}\cdot t$ - zeigen Sie also, dass $z_{_{I}}\cdot b_{_{I}}=b_{_{I}}\cdot z_{_{I}}=e_{_{B}}$ gilt!

Hinweis: Zeigen Sie, dass $0_{_{B}}:=0_{_{A}}+I=z_{_{I}}\cdot b_{_{I}}-e_{_{B}}$ und erläutern Sie den Zusammenhang zur Definition des Ideals $I$ !

Topologisierung der Algebraerweiterung

Die Algebraerweiterung wird mit einer Quotientennorm versehen, die wie folgt definiert ist:

\|q_{_{I}}\|_{B}:=\|q+I\|_{B}:=\displaystyle \inf _{r\in I}\|\!|q+r|\!\|_{D}

Dabei bezeichnen man die Nebenklassen in Kurzform mit $q_{I}\in B$ , wobei diese Mengen wie folgt definiert sind:

q_{_{I}}:=q+I:=\{q+r\,:\,r\in I\}

Man muss hier keine Linknebenklassen und Rechtnebenklassen unterscheiden, da die Addition in einem Vektorraum kommuntativ ist.

Stetigkeit Algebrahomomorphismus

Sei $x\in A$ beliebig gewählt, dann gilt mit der Norm $\|\cdot \|_{B}$ auf dem Quotientenraum $B:=A[t]/I$ die folgende Abschätzung

{\begin{array}{rcl}\|\tau (x)\|_{B}&=&\|x_{I}\|_{B}=\|x+I\|_{B}:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{D}\\&\leq &\|\!|x+0_{A[t]}|\!\|_{D}=D^{0}\cdot \|x\|_{A}=\|x\|_{A}\end{array}}

Damit ist $\tau$ stetig (siehe Stetigkeitssatz für lineare Abbildungen).

Struktur der Polynome aus dem Ideal

Betrachten nun das Bild $\tau (A)\subset B$ von $\tau$ in $B$ . Sei nun $A'=\tau (A)=\{x_{I}\,:\,x_{I}=x+I=\tau (x)\}$ gegeben und man betrachtet die Abschätzung für ein beliebiges $q\in A[t]$ mit $r=o\cdot q\in I$ mit $o(t)=z\cdot t-e_{A}$ . Dabei gilt:

{\begin{array}{rcl}r(t)&=&\displaystyle \sum _{k=0}^{\infty }r_{k}\cdot t^{k}=o(t)\cdot q(t)\\&=&-q_{0}+\sum _{k=1}^{\infty }(z\cdot q_{k-1}-q_{k})\cdot t^{k}\end{array}}

Stetigkeit der Umkehrabbildung der Einbettung

Unter Verwendung der Abschätzung $\|x\|_{A}\leq D\cdot \|z\cdot x\|_{A}$ erhält man

{\begin{array}{rcl}\|\!|x+r|\!\|_{D}&=&D^{0}\cdot \|x-q_{0}\|_{A}+\sum _{k=1}^{\infty }D^{k}\cdot \|z\cdot q_{k-1}-q_{k}\|_{A}\\\\&\geq &D^{0}\cdot \|x-q_{0}\|_{A}+\sum _{k=1}^{\infty }D^{k}\cdot \left(\|z\cdot q_{k-1}\|_{A}-\|q_{k}\|_{A}\right)\\\\&\geq &D^{0}\cdot \|x-q_{0}\|_{A}+\sum _{k=1}^{\infty }D^{k}\cdot \|z\cdot q_{k-1}\|_{A}-D^{k}\cdot \|q_{k}\|_{A}\\&\geq &\|x-q_{0}\|_{A}+\sum _{k=1}^{\infty }D^{k-1}\cdot \|q_{k-1}\|_{A}-D^{k}\cdot \|q_{k}\|\\&\geq &\|x-q_{0}\|_{A}+\|q_{0}\|_{A}\geq \|x\|_{A}\end{array}}

Teleskopierende Summen

Bei teleskopierenden Summen werden Summen betrachtet, wobei die Summanden selbst Differenzen sind. Aufeinanderfolgende Teilterme heben sich dabei auf. In der obigen Abschätzung bilden die Terme

D^{k-1}\cdot \|q_{k-1}\|-D^{k}\cdot \|q_{k}\|

eine Telekopsumme.

Infimumbildung

Durch Infimumbildung über alle Polynome $r\in I$ bleibt die obige Ungleichung erhalten. $\|x+I\|_{B}:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{D}\geq \|x\|_{A}$

Umgekehrte Abschätzung

Für die Stetigkeit der Umkehrabbildung $\tau ^{-1}$ gilt bzgl. dem Nullpolynom $0_{A[t]}\in I$ :

\|x+I\|_{B}:=\displaystyle \inf _{r\in I}\|\!|x+r|\!\|_{D}\leq \|\!|x+0_{A[t]}|\!\|_{D}=D^{0}\cdot \|x\|_{A}=\|x\|_{A}

Insgesamt ist der Algebraisomorphismus der Einbettung von $A$ in $A'\subset B:=A[t]/I$ eine Isometrie mit $\|x+I\|_{B}=\|x\|_{A}$ .

Vervollständigung

Zunächst einmal vervollständigt man die Polynomalgebra $(A[t],\|\!|\cdot |\!\|_{D})$ zu einer Potenzreihenalgebra $({\overline {A[t]}},\|\!|\cdot |\!\|_{D})$ , wobei die Menge der Polynome aus $A[t]$ dicht in ${\overline {A[t]}}$ bzgl. der Norm $\|\!|\cdot |\!\|_{D}$ mit:

{\overline {A[t]}}:=\left\{p\in A^{\infty }[t]\,:\,\|\!|p|\!\|_{D}:=\sum _{k=0}^{\infty }D^{k}\cdot \|p_{k}\|_{A}<\infty \right\}

Cauchy-Folgen in der Polynomalgebra

Sei $(p^{(m)})_{m\in \mathbb {N} }\in A[t]^{\mathbb {N} }$ eine Cauchy-Folge von Polynomen in $A[t]$ mit der Eigenschaft:

p^{(m)}(t):=\sum _{k:=0}^{\infty }p_{k}^{(m)}\cdot t^{k}{\mbox{ mit }}\left(p_{k}^{(m)}\right)_{k\in \mathbb {N} _{0}}\in c_{oo}(A)

und der Cauchy-Folgen-Eigenschaft

\forall _{\varepsilon >0}\quad \exists _{N_{\varepsilon }\in \mathbb {N} }\quad \forall _{m,n\geq N_{\varepsilon }}\,\colon \,\quad \|\!|p^{(m)}-p^{(n)}|\!\|_{D}<\varepsilon

.

Vervollständigung der Polynomalgebra

Wenn ein $z\in A$ in der Algebraerweiterung $B_{0}$ invertierbar ist, dann ist $z\in A$ auch in der Vervollständigung $B_{0}\subseteq B:={\overline {B_{0}}}$ als Algebraerweiterung invertierbar. Jeder metrische Raum lässt sich vervollständigen und jeder normierte Raum ist auch ein metrische Raum.