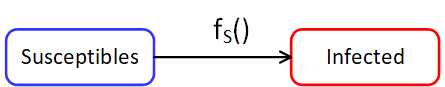COVID-19/Mathematische Modellierung/Kompartimentmodelle

SIR Model - Animation

Kompartimentmodelle in der Epidemiologie

In der Biologie werden alle gleichartigen Zellräume häufig in einer Gruppe zusammengefasst und als Kompartimente bezeichnet.

Betrachtet man die Effekte zwischen Kompartimenten, spricht man von Compartiment Models.

Beispielsweise kann man eine Diffusion als Austausch zwischen zwei Kompartimenten, welche durch eine Membran getrennt sind, beschreiben.

Die Aufteilung einer Population in Kompartimente ist eine gängige Technik zur mathematischen Modellierung von Infektionskrankheiten und wird auch häufig bei COVID-19 eingesetzt.

Warnhinweis: Die Beispielrechnungen und -Werte dienen lediglich zu Lehrzwecken. Sie dürfen nicht zu Zwecken der Vorhersage verwendet werden.

Das SI-Modell

Ein sehr einfaches Kompartiment-Modell ist die Unterteilung einer Population in lediglich zwei Kompartimente:

• Anteil der Nicht-Infizierten $S$ (Susceptible) an der Gesamtbevölkerung N: Eine Zahl zwischen 0 und 1
• Anteil der Infizierten $I$ (Infected)

In der Gruppe $I$ befinden sich Individuen, welche einmal durch den Erreger infiziert wurden (unabhängig davon, ob sie Symptome zeigen oder nicht).

Susceptibles können von dem Kompartiment $S$ durch eine Infektion in das Kompartiment $I$ wechseln.

Die Individuen in den Kompartimenten werden also lediglich durch das Merkmal "Besitz eines Erregers" unterschieden.

Bei diesem einfachen Modell kehren Individuen nicht aus dem $I$ -Kompartiment zum $S$ -Kompartiment zurück.

Die Infektionsfunktion

Im Kompartiment-Bild zeigt ein Pfeil an, dass Individuen von einem Kompartiment zu einem anderen wechseln.

Eingehende Pfeile zeigen eine Zunahme an. Entsprechend werden ausgehende Pfeile aus einem Kompartiment negativ gezählt.

Wir definieren eine Infektions-Funktion ${\textstyle f_{S}()}$, die den Wechsel der Individuen in das Infected-Kompartiment mit einer bestimmten Rate beschreibt.

Diese Rate entspricht der Ableitung von $I$ nach der Zeit:

$f_{S}()={\frac {dI}{dt}}={\dot {I}}$

Exponentielles Wachstum

Eine sehr einfache Annahme besteht darin, dass jeder Infizierte Susceptibles (aus einem unendlichen Vorrat) mit einer festen Rate infiziert.

Dann hätten wir als Infektions-Funktion

$f_{S}()={\dot {I}}=\beta \cdot I$

umgeformt

${\dot {I}}-\beta \cdot I=0$

Dies ist eine Differentialgleichung mit der Lösung

$I(t)=C_{e}\cdot e^{\beta \cdot t}$,

also exponentielles Wachstum mit einer Infektionskontaktrate $\beta$ und $C_{e}$ als Anteil an Infizierten am Tag 0.

Hier können Sie weitere Materialien zum exponentiellen Wachstum ansehen.

Berücksichtigung endlich vieler Susceptibles

Während die Annahme eines unendlichen Vorrats an $S$ zu Beginn einer Epidemie noch gültig sein mag, ist bei weiterem Fortschreiten zu erwarten, dass der Anteil der $S$ zurückgeht.

Die Infektions-Funktion wird dann sowohl proportional zu $S$ als auch zu $I$ angenommen:

$f_{S}()={\dot {I}}=\beta \cdot S\cdot I$

Da wir $S$ und $I$ als Anteile formuliert haben, können wir den Wert von $\beta$, den wir aus der Exponentialfunktion abgeschätzt haben, übernehmen (unverändertes Kontakt- und Hygiene-Verhalten vorausgesetzt).

Dann haben wir eine Gleichung für den Zufluss

${\dot {I}}=\beta \cdot I\cdot S$

und eine Gleichung für den Wegfluss

${\dot {S}}=-\beta \cdot S\cdot I$

Diese beiden Gleichungen müssen wir jetzt in einen Zusammenhang bringen.

Die Erhaltungsgleichung

Im Fall von Epidemien nimmt man an, dass von außen keine neuen Individuen hinzukommen oder weggehen.

Soll auch das berücksichtigt werden, spricht man von Endemie-Modellen.

Im Epidemiefall haben wir eine Erhaltungsgleichung ${\textstyle S+I=1}$.

Daraus folgt: ${\textstyle {\dot {I}}+{\dot {S}}=0}$ bzw. ${\textstyle {\dot {S}}=-{\dot {I}}=-f()}$.

Die Logistische Funktion

Mit ${\textstyle S=1-I}$ wird obige Gleichung zu

${\frac {dI}{dt}}=-\beta \cdot I\cdot (I-1)$

Diese Gleichung nennt man logistische Differentialgleichung, für die man eine Lösung (Logistische Funktion) angeben kann:

$I(t)={\frac {1}{1+Ce^{-\beta \cdot t}}}$

Nimmt man nun die Infektionszahlen für den Tag Null (24. Februar 2020, 16 Infizierte) ${\textstyle I(0)=16/83Mio.}$, erhält man ${\textstyle C=5,19\cdot 10^{6}}$.

Am Tag 10 (5.März 2020) waren es 400 Infizierte. Dadurch ergibt sich ${\textstyle \beta =0,3219}$.

Hiernach wäre zu Beginn der Infektion bei exponentiellem Wachstum etwa alle ${\frac {ln(2)}{0,3219}}\approx 2$ Tage von einem Infizierten eine Übertragung erfolgt.

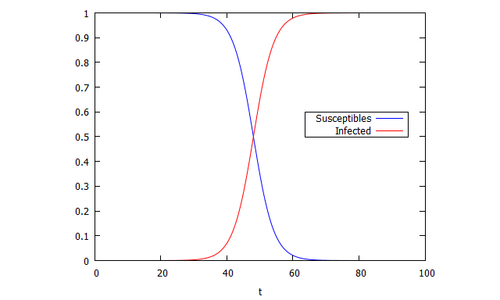
Man kann entsprechend diesem Modell (und der doch recht einfachen Abschätzung der Parameter) ablesen, dass am Wendepunkt der Kurve nach ca. 47 Tagen die Hälfte der Bevölkerung infiziert ist.

An diesem Tag wäre die Infektionsrate auf auf ihren Maximalwert von fast 8% der Gesamtbevölkerung an einem einzigen Tag (!!) angestiegen.

Die Krankenhäuser könnten eine solche Fallzahl nicht ansatzweise verkraften. Diese Entwicklung kann jedoch teilweise gesteuert werden durch Massnahmen wie Kontaktverringerung etc. .

Dann sich die Parameter einiger Zeit während dies mit den Gleichungen schwierig zu bewerkstelligen ist, kann eine solche Berechnung mit Maxima recht leicht durchgeführt werden.

Lösung der Gleichung mit Maxíma

Das Prinzip der Berechnung basiert auf dem Verfahren von Euler.

Zu Beginn setzen wir einen Startwert ${\textstyle I_{0}}$ in die Differentialgleichung ein und erhalten den Wert der Ableitung an der Stelle ${\textstyle I_{0}}$:

${\frac {d\,I_{0}}{dt}}=-\beta \cdot I_{0}\cdot (I_{0}-1)$

Damit können wir den Wert von ${\textstyle I_{1}}$ berechnen über:

$I_{1}=I_{0}+{\frac {d\,I_{0}}{dt}}\cdot \Delta t$

Mit dem Wert für ${\textstyle I_{1}}$ gehen wir wieder in die Differentialgleichung und bestimmen den Wert ${\textstyle {\dot {I_{2}}}}$, um daraus wiederum ${\textstyle I_{2}}$ zu berechnen.

Dieses Vorgehen wird solange wiederholt, bis "der gewünschte Blick in die Zukunft" weit genug ist.

Wir verwenden bei Maxima eine Variante des Euler-Verfahrens, das Runge-Kutta-Verfahren.

Für die Verwendung des Runge-Kutta-Verfahrens muss die Differentialgleichung nach der höchsten vorkommenden Ableitung aufgelöst sein, was in unserer Gleichung bereits der Fall ist.

Bei Maxima steht beim zugehörigen rk()-Befehl in der ersten eckigen Klammer die rechte Seite der Differentialgleichung.

In die zweite eckige Klammer kommt der Name der zu integrierenden Variablen (${\textstyle I}$), gefolgt vom Startwert.

In der letzten eckigen Klammer steht zuerst der Name der unabhängigen Variablen, gefolgt von der Untergrenze, danach die Obergrenze und schließlich die Schrittweite der Integration:

/*SI-Modell*/
beta: 0.3219;
I0: 1.93E-07;
sol: rk([-beta*I*(I-1) ],[I],[I0],[t,0,100,0.1])$   
plot2d ([[discrete,makelist([p[1],1-p[2]],p,sol)],
         [discrete,makelist([p[1],p[2]],p,sol)]],
         [xlabel,"t"],
         [legend,"Susceptibles","Infected"],
         [color, blue, red],
         [gnuplot_preamble, "set key box at 95.,.6" ])$

Möchte man nun den letzten Wert von ${\textstyle I}$ nach 80 Tagen aufrufen, gibt man einfach ein:

sol[801][2];

(Bei Maxima beginnnt die Zählung ab Index 1.)

Das SIR-Modell

Beim vorigen SI-Modell infiziert ein Mitglied von ${\textstyle I}$ mit einer konstanten Infektionskontaktrate ${\textstyle \beta }$ "endlos" weiter.

Dies ist natürlich eine grobe Vereinfachung, der man durch die Einführung der Klasse ${\textstyle R}$ (Removed) im Kompartiment-Modell abhelfen will.

Die Erhaltungsgleichung wird um den Anteil ${\textstyle R}$ erweitert: ${\textstyle S+I+R=1}$.

Die Infektionsfunktion übernimmt man unverändert aus dem SI-Modell.

Die Gesundungs-Funktion führt nun Anteile aus ${\textstyle I}$ nach ${\textstyle R}$ mit einer Genesungsrate ${\textstyle \gamma }$ über:

${\frac {dR}{dt}}={\dot {R}}=f_{I}()=\gamma \cdot I$

Statistisch gesehen wird hier eine Exponentialverteilung mit dem Erwartungswert einer Gesundungsdauer ${\textstyle T_{G}={\frac {1}{\gamma }}}$ beschrieben.

Ist der Erwartungswert der Genesungsdauer beispielsweise 7 Tage, dann beträgt der Anteil der Infizierten nach 7 Tagen (angenommen, es sind keine weiteren Infektionen hinzugekommen), noch ${\textstyle {\frac {1}{e}}\approx 37\%}$.

Beim SIR-Modell kommen also zum einen neue Infizierte hinzu (${\textstyle S\rightarrow I}$, genauso wie beim SI-Modell), andere wechseln in die Gruppe (${\textstyle I\rightarrow R}$):

${\frac {dI}{dt}}={\dot {I}}={\dot {S}}-{\dot {R}}=f_{S}()-f_{I}()=\beta \cdot S\cdot I-\gamma \cdot I$

Damit haben wir ein kleines System von Differentialgleichungen mit

${\textstyle {\dot {S}}=-\beta \cdot S\cdot I}$

${\textstyle {\dot {I}}=\beta \cdot S\cdot I-\gamma \cdot I}$

${\textstyle {\dot {R}}=\gamma \cdot I}$

Wegen $R+S+I=1$ ergibt sich ${\dot {R}}+{\dot {S}}+{\dot {I}}=0$.

Damit ergibt sich die dritte Differentialgleichung auch aus ${\dot {R}}=-{\dot {S}}-{\dot {I}}$. Sie braucht daher nicht integriert zu werden.

Das SIR-Modell wurde bereits 1927 von Kermack und McKendrick Kermack und McKendrick formuliert:

Lösung des Gleichungssystems mit Maxima

Auch Differentialgleichungssysteme lassen sich mit der rk()-Funktion leicht lösen. In den Klammern werden lediglich mehrere Gleichungen hintereinander eingefügt und durch Kommata getrennt:

/*SIR-Modell*/
beta: 0.3219;
gamma: 0.1;
I0: 1.93E-07;
sol: rk([ -beta*S*I ,
           beta*S*I-gamma*I],
           [S,I],
           [(1-I0),I0],
           [t,0,160,1])$
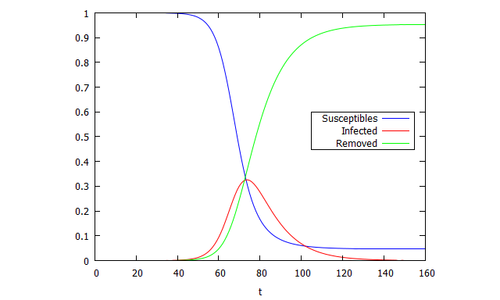
plot2d ([[discrete,makelist([p[1],p[2]],p,sol)],
         [discrete,makelist([p[1],p[3]],p,sol)],
         [discrete,makelist([p[1],1-p[3]-p[2]],p,sol)]] ,
         [xlabel,"t"],
         [legend,"Susceptibles","Infected","Removed"],
         [color, blue, red,green],
         [gnuplot_preamble, "set key box at 155.,.6" ])$

Nach dieser Berechnung liegt bei 75 Tagen das Maximum der Infektionen. Hiernach wären beängstigende 30% der Bevölkerung infiziert.

Die Basisreproduktionszahl

Eine oft genannte Kenngröße bei Epidemien ist die Basisreproduktionszahl ${\textstyle R_{0}}$. Sie gibt an, wie viele Andere eine Infizierte Person während der Phase der Infektiosität durchschnittlich ansteckt.

Beispielhafte Basisreproduktionszahlen sind:

• Malaria: mehr als 1000
• Masern: 15 bis 18
• Pocken, Polio: 6 bis 8
• Keuchhusten 14
• Grippepandemie von 1918: 2 bis 3
• COVID-19 (geschätzt): 2,4 bis 3,3

Für das SIR-Modell gilt :

$R_{0}={\frac {\beta }{\gamma }}$.

Mit den Werten für ${\textstyle \beta =0,3219}$ und ${\textstyle \gamma =0,1}$ würden wir als ${\textstyle R_{0}=3,219}$ erhalten. Dies liegt innerhalb der Schätzwerte ${\textstyle 2,4<R_{0}<3,3}$.

Das SEIR-Modell

Bei vielen Infektionen sind die Betroffenen selbst nicht sofort infektiös, sondern erst nach einer Latenzzeit.

Um diesen Zustand zu modellieren, führt man ein weiteres Kompartiment $E$ vor $I$ ein.

${\textstyle S+E+I+R=1}$

Die Infektions-Funktion führt dann $S$-Anteile in $E$-Anteile über:

$f_{S}()={\dot {E}}=\beta \cdot S\cdot I$

Eine weitere Latenz-Funktion führt dann $E$-Anteile in $I$-Anteile über:

$f_{E}()={\dot {I}}=\alpha \cdot E$

Statistisch gesehen wird auch hier eine Exponentialverteilung beschrieben.

Die Gesundungs-Funktion führt nun wie oben Anteile aus ${\textstyle I}$ nach ${\textstyle R}$ mit einer Genesungsrate ${\textstyle \gamma }$ über:

${\frac {dR}{dt}}={\dot {R}}=f_{I}()=\gamma \cdot I$

Dann haben wir das System von Diiferentialgleichungen:

${\textstyle {\dot {S}}=-\beta \cdot S\cdot I}$

${\textstyle {\dot {E}}=\beta \cdot S\cdot I-\alpha E}$

${\textstyle {\dot {I}}=\alpha E-\gamma I}$

${\textstyle {\dot {R}}=\gamma I}$

Die letzte Gleichung können wir wiederum wegen der Erhaltungsgleichung ${\textstyle S+E+I+R=1}$ und ${\textstyle {\dot {S}}+{\dot {E}}+{\dot {I}}+{\dot {R}}=0}$ weglassen.

Lösung des Gleichungssystems mit Maxíma

Die Lösung dieses Gleichungssystems geht analog zum SIR-Modell:

/*SEIR-Modell*/
N:8.3E7;
alpha: 0.5; 
beta: 0.3219; 
gamma: 0.1; 
I0:  1.93E-07;
sol: rk([-beta*S*I,
         beta*S*I-alpha*E,
         alpha*E-gamma*I],
         [S,E,I],[(1-I0),0,I0],
         [t,0,160,0.1])$;
plot2d ([[discrete,makelist([p[1],p[2]],p,sol)],
         [discrete,makelist([p[1],p[3]],p,sol)],
         [discrete,makelist([p[1],p[4]],p,sol)],
         [discrete,makelist([p[1],(1-p[4]-p[3]-p[2])],p,sol)]] ,
         [xlabel,"t"],
         [legend,"Susceptibles","Exposed","Infected","Removed"],
         [color,blue,magenta,red,green],
         [gnuplot_preamble, "set key box at 70.,.6" ])$;

Beim Verlauf der $I$-Kurve kann man sehen, dass das Maximum 35 Tage später auftritt mit einem ca. 5% geringeren Wert als beim SIR-Modell. Dies wären 22 Mio. Infizierte in Deutschland.

Wenn man annimmt, dass die Hälfte der Intensivstationen für andere schwere Krankheiten benötigt werden, liegt die Chance eines schwer an Covid-19 Erkrankten auf einen Platz in einer Intensivstation bei kärglichen 5 %!

Setzt man $\alpha$ auf den Wert 1, ist das Maximum etwa 20 Tage früher und etwa 2% geringer als beim SIR-Modell. Das E-Kompartiment hat also zwar eine verzögernde, aber keine wesentlich abschwächende Funktion.

Vor allem aber ist sie nicht durch Verhaltensänderungen steuerbar.

Kontaktreduktion

Nun interessiert uns, wie sich der Verlauf ändert, wenn wir nach einigen Tagen einen Parameter ändern. Beispielsweise wollen wir nach 60 Tagen die Infektionskontaktrate auf ein Drittel des ursprünglichen Werts setzen.

Hierzu führen wir die rk()-Rechnung für 60 Tage durch. Danach wird der Parameter $\beta _{2}=\beta _{1}/3$ gesetzt.

Danach wird die rk()-Rechnung erneut aufgerufen. Die Randwerte werden aus den Parametern der vorangegangenen Rechnung übergeben. Beispielsweise ist sol[601][2] der $S$-Wert nach 60 Tagen (unsere Schrittweite war 0,1).

In der Graphik ist die y-Achse in Bevölkerungszahlen für Deutschland dargestellt. Etwas mehr als 1 % der Infizierten bedürfen einer Behandlung in einer der ca. 14 000 Intensivstationen.

/*SEIR-Modell mit phasenweiser Aenderung von Gamma; N*/
N:8.3E7;
alpha: 0.5;
beta1: 0.3219; 
gamma: 0.1;
I0: 1.93E-07;
dateofchange: 60;
sol1: rk([-beta1*S*I,
          beta1*S*I-alpha*E,
          alpha*E-gamma*I],
          [S,E,I],[(1-I0),0,I0],[t,0,dateofchange,0.1])$;
beta2: beta1/3;
sol2: rk([-beta2*S*I,
          beta2*S*I-alpha*E,
          alpha*E-gamma*I],
          [S,E,I],
          [sol1[dateofchange*10+1][2],sol1[dateofchange*10+1][3],sol1[dateofchange*10+1][4]],
          [t,dateofchange,90,0.1])$;
plot2d ([discrete,makelist([p[1],p[3]*8.3E7],p,sol1)],
        [discrete,makelist([p[1],p[4]*8.3E7],p,sol1)],
        [discrete,makelist([p[1],8.3E7*(1-p[4]-p[3]-p[2])],p,sol1)],
        [discrete,makelist([p[1],p[3]*8.3E7],p,sol2)],
        [discrete,makelist([p[1],p[4]*8.3E7],p,sol2)],
        [discrete,makelist([p[1],8.3E7*(1-p[4]-p[3]-p[2])],p,sol2)]] ,
        [xlabel,"t"],
        [legend,"Exposed","Infected","Removed","","",""],
        [color, magenta,red,green, magenta,red,green],
        [gnuplot_preamble, "set key box at 40.,3E5" ])$;

Man sieht, dass nach 60 Tagen die Exposed-Kurve zurückgeht und dann wieder langsam steigt.

Über einen längeren Zeitraum bliebe die Infected-Kurve dann unter 250 000 Infizierten, die Situation mit reduzierten Kontakten würde sich dann aber über 2,5 Jahre hinziehen.

Dies darf jedoch nicht verwundern, da mit einer Durchseuchung gerechnet werden muss ist und die Gesundungsdauer nicht wesentlich beeinflusst werden kann.

Verfeinerungsmöglichkeiten

Jetzt, wo wir das Grundgerüst haben, können wir weitere Verfeinerungen vornehmen und das Modell perfektionieren.

• Wir könnten die Erhaltungsgleichung ändern und eine Geburtenrate sowie Sterberate hinzufügen. Dann hätten wir ein Endemiemodell.
• Wir könnten die Übergangsfunktionen näher an die beobachteten zeitlichen Verläufe anpassen (z.B. normalverteilt mit Mittelwert und Varianz)
• Wir könnten die Bevölkerung in Altergruppen einteilen und die Übergänge zwischen den Gruppen mit jeweils altersspezifischen Faktoren versehen.
• Wir könnten die Bevölkerungsdichte berücksichtigen und verschiedene Kompartimente mit Gebieten hoher und geringer Dichte einführen, um verschiedene Kontaktraten nachzubilden.

Aufgaben für Lernende

• Analysieren Sie die Verfügbarkeit von Daten aus statistischen Quellen und stellen Sie dar, wie man Prognosen aus diesen Daten erstellen kann! Welche Problem sehen Sie bei den Daten?
• Wie groß ist die Infektionskontaktrate $\beta$ beim exponentiellen Verlauf, wenn sich die Zahl der Infizierten nach 4 Tagen (= die mittlere Zeit zwischen Kontakten) verdoppelt hat?
• Wie groß ist die Infektionskontaktrate $\beta$ beim SI-Modell, wenn die größte Zunahme an Infektionen nach 100 Tagen erfolgt? Wie groß ist $\beta =$ für 200 Tage?
• Wie groß ist beim SIR-Modell der Anteil der Infizierten bei einer angenommenen Gesundungsrate $\gamma =0.1\,Tag^{-1}$ nach fünf Wochen, wenn keine weiteren Infektionen hinzukommen?
• Angenommen, Infizierte werden beim SIR-Modell jeweils nach exakt 10 Tagen wieder gesund. Wie könnte man eine Gesundungs-Funktion beschreiben? Wie ließe sich dieses Modell in Maxima implementieren?
• (Animationen) Animationen können die Prozesse in Lernumgebungen veranschaulichen. Welche weiteren Animationen sind für diese Lernumgebung hilfreich? Analysieren Sie dazu die Möglichkeiten 2D-Animationen zu erstellen!
• (Dynamische Dokumentengenerierung) Analysieren Sie die Möglichkeiten der dynamischen Generierung von Dokumenten auf Basis einer sich stetig ändernden Datenbasis. Erläutern Sie die Bedeutung für die epidemiologische Modellbildung!

Siehe auch

• 2D-Animationen