Fachbereich Physik/Klassische Elektrodynamik/Maxwell-Einführung
Dieser Text ist noch in Bearbeitung. Vor Änderungen bitte mit dem Verfasser Kontakt aufnehmen oder eine Diskussion beginnen.
Der folgende Text enthält eine Einführung in die maxwell'schen Gleichungen für Oberstufenschüler, Studienanfänger und andere Interessierte. Der volle mathematische Formalismus befindet sich im Wikipedia-Artikel w:Maxwellsche Gleichungen.
Was müssen Sie wissen, um den folgenden Text zu verstehen?
- Sie wissen, was eine Ableitung ist. Wie in vielen Bereichen der Physik üblich, verwenden wir in diesem Artikel für die Ableitungen eine Differentialschreibweise. Sie kennen wahrscheinlich die Ableitung einer Funktion als schreiben. Wir schreiben hier .
- Sie wissen, was ein Integral ist. Hier werden wir nicht nur eine Funktion integrieren sondern auch über eine Fläche oder eine Linie im Raum. Das wird aber in diesem Text am ersten Beispiel knapp erläutert.
- Sie brauchen zum Grundverständnis keine genauen Kenntnisse über Vektoranalysis. Wir schreiben die Gleichungen zwar vektoriell auf, aber es reicht, wenn Sie sich Felder vorstellen, die senkrecht durch Flächen hindurchgehen. Die Vektoranalysis sorgt dafür, dass die Beziehungen auch im allgemeinen Fall "schräger" Felder stimmen.
An physikalischem Wissen müssen Sie folgendes mitbringen:
- Sie wissen, dass ein elektrisches Feld Ladungen verschieben kann. Man kann eine Verschiebungsdichte als pro Fläche verschobene Ladung definieren.
- Sie wissen, dass ein sich änderndes Magnetfeld in einer Leiterschleife eine Induktionsspannung hervorruft.
- Sie wissen, dass ein stromdurchflossener Leiter von einem Magnetfeld umgeben ist. Im ungestörten Fall bilden sich ringförmige Feldlinien um den Leiter.
Willkommen an Bord!
Der Autor freut sich über konstruktive Rückmeldungen, insbesondere über Fehlerkorrekturen.
Verschiebungsdichte und Feldstärke des Elektrischen Felds - Die erste maxwellsche Gleichung
[Bearbeiten]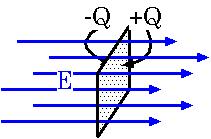
Man stellt fest, dass ein elektrisches Feld an jeder Stelle eine Ladungsverschiebung hervorruft. Diese Ladungsverschiebung (Ladung pro Fläche in Coulomb pro Quadratmeter) ist proportional zur Feldstärke in Newton pro Coulomb oder Volt pro Meter.
Hier wird man sehr oft verwendet. Man stellt fest: Wer ist man, wodurch stellt fest (Versuch), wie stellt fest?
Der Proportionalitätsfaktor ist eine universelle Konstante, die w:Permittivität oder Dielektrizitätskonstante.
Man kann diesen Term umformen und erhält das Produkt aus elektrischer Feldstärke und Fläche. Das ist eine Größe, die man analog zu einer entsprechenden Größe beim Magnetfeld als elektrischen Fluss bezeichnen kann. Die Vorstellung einer elektrischen Größe, die analog zu einer Flüssigkeit eine Fläche durchfließt, war der Ausgangspunkt für die Formulierung der Gleichungen analog zur Strömungsdynamik. Wieder "man"

Nun gilt diese Formel nur dann, wenn über die Fläche konstant ist. Ist das nicht der Fall, muss man ein Flächenintegral verwenden. Dies liefert die erste maxwell'sche Gleichung:
Dabei ist nun eine geschlossene Fläche (das ist eine Fläche ohne "Rand", die einen Raum vollständig umschließt, in einem einfachen Fall eine Kugelfläche). Diese Formel kann umgeformt werden, so dass die Ladungsdichte statt der Ladung auftritt, näheres dazu siehe im Wikipedia-Artikel. Die Abbildung rechts zeigt einen zweidimensionalen Schnitt durch eine dreidimensionale Oberfläche.
Das Integral bedeutet hier, dass die Gesamtfläche in kleine Flächenstückchen zerlegt wird, dass in jedem dieser Flächenelemente das Produkt gebildet wird und alle diese Werte aufsummiert werden. Für das Grundverständnis der Gleichung genügt es, wenn Sie sich ein über die Fläche homogenes Feld vorstellen. Dann schrumpft das Integral wieder zu einem einfachen Produkt: . Das Integral sorgt lediglich dafür, dass die Beziehung auch im Fall inhomogener Felder stimmt.
Interpretation
[Bearbeiten]Diese Gleichung sagt aus, dass der elektrische Fluss durch die Oberfläche eines Raumvolumens proportional der umschlossenen Ladung ist. In anderen Worten: jede Ladung im Raum erzeugt einen elektrischen Fluss.
Anwendung
[Bearbeiten]Nehmen wir an, die Ladung befinde sich im Zentrum einer Kugelfläche mit dem Radius . In jedem ihrer Flächenelemente ist aus Symmetriegründen der elektrische Fluss gleich, so dass man auf das Integral verzichten kann. Für kann man die Kugeloberfläche einsetzen. Löst man diesen Term nach auf:
erhält man das Coulombsche Gesetz.
Das Magnetfeld und die zweite maxwellsche Gleichung
[Bearbeiten]
In einem elektrischen Feld kann eine geschlossene Fläche ein Volumen enthalten, in dem sich überschüssige positive oder negative Ladungen befinden. Die Folge ist, dass durch diese Fläche ein elektrischer Fluss auftritt. Im Gegensatz dazu enthält bei einem Magnetfeld ein Volumen immer gleichermaßen Nord- und Südpol, es gibt keine isolierten magnetischen Pole, die sich als Überschuss in einem Raumvolumen befinden können.
Durch jede geschlossene Fläche im Raum ist deshalb die Summe des magnetischen Flusses null. Dies ist die Aussage der zweiten maxwellschen Gleichung:
Auch hier enthält die Abbildung einen zweidimensionalen Schnitt durch eine dreidimensionale Struktur.
Interpretation
[Bearbeiten]Anschaulich kann man formulieren: Feldlinien, die ein Volumen durch die geschlossene Fläche A verlassen, müssen auch wieder in das Volumen durch diese Fläche hineinlaufen. Es gibt nur geschlossene Feldlinien. Bei dieser Argumentation muss man sich allerdings immer im Klaren sein, dass Feldlinien Richtungen von Kräften angeben und keine zählbaren Größen sind!
Anwendung
[Bearbeiten]?
Faradays Induktionsgesetz und die dritte maxwell'sche Gleichung
[Bearbeiten]Das Induktionsgesetz als Integral
[Bearbeiten]Das Induktionsgesetz sagt, dass die induzierte Spannung gleich der zeitlichen Änderung des magnetischen Flusses ist:
Analog zum elektrischen Fluss ist der magnetische Fluss als das eine Fläche A durchdringende magnetische Feld definiert. Im einfachsten Fall, wenn B über die gesamte Fläche konstant ist, gilt:
Wenn man oben den magnetischen Fluss wieder durch seine Definition rück-ersetzt, erhält man das Induktionsgesetz als
Falls B über A nicht konstant ist, muss ein Integral verwendet werden:
Unter Berücksichtigung dieser Verallgemeinuerung lässt sich das Induktionsgesetz so schreiben:
Die Formulierung ist auf den ersten Blick verwirrend, weil hier die zeitliche Ableitung eines Integrals über eine Fläche gebildet wird. Man sieht jedoch leicht: Das Integral liefert den magnetischen Fluss über die offene Fläche . Eine offene Fläche ist eine Fläche mit "Rand", im einfachsten Fall eine ebene Kreisscheibe, sie kann jedoch auch eine beliebige, nicht ebene Form mit einem Rand sein, beispielsweise eine Halbkugel-Fläche oder ein Becherglas. Die Induktionsspannung ergibt sich nun einfach als Ableitung des magnetischen Flusses durch diese Fläche nach der Zeit.
Das elektrische Feld bei der Induktion
[Bearbeiten]In der letzten Formel des vorangegangenen Abschnitts taucht eine offene Fläche auf, über die das Magnetfeld integriert wird. Man kann diese Formel nun so interpretieren, dass die Induktionsspannung auftritt, wenn man längs des Rands dieser Fläche einen Umlauf vollführt.

In einem statischen Feld kann beim Durchlaufen einer geschlossenen Kurve keine Energie aufgenommen werden. Man landet immer auf dem gleichen Potential, wenn man sich wieder am Ausgangsort befindet. Das Ringintegral der Feldstärke über den Weg ist in einem statischen Feld immer Null. Durch das sich zeitlich ändernde Magnetfeld bei der Induktion entsteht nun ein elektrisches Wirbelfeld. Durchläuft eine Ladung den Rand der Fläche , erhält sie nach einem Umlauf die Energie . Sie befindet sich wieder am gleichen Ort aber auf einem anderen Potential, das sich vom Ausgangspotential gerade um die Induktionsspannung unterscheidet. Formal kann man dies so schreiben.
Gleichsetzen der beiden Ausdrücke für die Induktionsspannung liefert den induktiven Zusammenhang zwischen dem sich ändernden Magnetfeld und dem aus ihm entstehenden elektrischen Feld und damit die dritte maxwell'sche Gleichung:
oder einfacher:
Interpretation/Zusammenfassung
[Bearbeiten]Gegeben sei eine offene Fläche , beispielsweise eine Kreisscheibe, die von einem Magnetfeld durchsetzt ist. Die zeitliche Änderung dieses magnetischen Flusses ist gleich einer Induktionsspannung, die bei einem Umlauf um als Integral der elektrischen Feldstärke über den Weg auftritt.
Oder: Ein elektrisches Wirbelfeld tritt genau dann auf, wenn ein sich ändernder magnetischer Fluss vorhanden ist. Ein Kreislauf um eine Fläche führt dann nicht mehr zu einer Stelle mit dem gleichen Potential.
Die Existenz eines elektrischen Felds ist nicht an das Vorhandensein von Ladungen gebunden. Ein E-Feld kann alleine dadurch entstehen, dass sich der magnetische Fluss durch eine Fläche im Raum ändert.
Anwendung
[Bearbeiten]
Jeder Stromkreis bildet eine Leiterschleife. Im statischen Fall gilt das kirchhoff'sche Gesetz, dass sich alle Teilspannungen (alle Änderungen des Potentials) zu Null addieren, genannt die Maschenregel. Geht man vom Punkt A (siehe Schaltung, links) aus im Kreis und addiert alle Spannungen vorzeichenrichtig, ergibt sich:
Eine Induktivität in einem Stromkreis erzeugt die Selbstinduktionsspannung

Enthält der Stromkreis einen ohmschen Widerstand und eine Induktivität, ändert sich die Situation grundlegend. Nun gilt die Maschenregel nicht mehr. Alle Teilspannungen summieren sich zur Induktionsspannung:
In anderen Worten: Läuft man von A beginnend ein Mal im Kreis, so hat man einen Potentialunterschied in Höhe der Induktionsspannung zurückgelegt. Wendet man das ohmsche Gesetz an, erhält man eine Differentialgleichung, mit deren Hilfe man den Stromfluss durch diese Schaltung berechnen kann:
Ausblick: Die Lösung dieser Gleichung führt auf eine e-Funktion. Das Integral dieser Funktion ermöglicht, den Energiegehalt des Magnetfelds zu bestimmen.
Das Ampère'sche Gesetz, der Verschiebestrom und die vierte maxwell'sche Gleichung
[Bearbeiten]Die vierte maxwell'sche Gleichung ist nicht - wie die anderen - eine neue Formulierung der bekannten Zusammenhänge mit anderen mathematischen Mitteln. Hinter der vierten Gleichung steckt eine neue physikalische Erkenntnis, weshalb es sich lohnt, diese Gleichung besonders gründlich zu betrachten.
Bekanntlich erzeugt sich bewegende Ladung, also ein Strom, ein Magnetfeld. Im Falle eines langen, geradlinigen Leiters ohne andere Objekte in der Nähe ergibt sich das Bild eines konzentrischen (genauer: zylindrischen) Felds. Die Feldstärke ist dabei
Sie ist also proportional dem Strom und indirekt proportional dem Abstand. Man erkennt unter dem Bruchstrich einen Kreisumfang und kann umformen:
Das bedeutet etwas ziemlich Phantastisches: Multipliziert man das Magnetfeld mit der Länge einer Kreislinie, erhält man eine Größe, die proportional der Stromstärke ist, die man umfahren hat. Diese Beziehung gilt allerdings nicht nur bei Kreislinien sondern auch bei beliebigen geschlossenen Kurven und sie gilt auch, wenn das magnetische Feld nicht immer senkrecht auf dem zurückgelegten Wegelement steht. Dieser Zusammenhang lässt sich wieder als Integral schreiben:
Diese Formel heißt das ampère'sche Gesetz. Interpretieren wir diese Formel:

Gegeben ist eine offene Fläche im Raum. Das ist eine Fläche mit einem Rand. Wir können uns einfach eine Kreisscheibe oder ein Quadrat vorstellen. Die Fläche kann aber auch nicht-eben sein, beispielsweise ein Duschvorhang oder eine Plastiktüte ohne Grifflöcher. Integrieren wir nun das Magnetfeld entlang des Rands, erhalten wir einen Wert, der proportional zum Strom ist, der die Fläche durchdringt. Und zwar unabhängig davon, ob die Fläche eben ist oder irgend wie "gebauscht". So lange wir den Rand nicht ändern, können wir die Fläche beliebig verformen, das Integral wird immer den gleichen Wert liefern. Das Bild links zeigt den einfachen Fall einer von einem Strom "durchstoßenen" Kreisscheibe.
Betrachten wir nun zwei Punkte in der Nähe eines Plattenkondensators, der gerade aufgeladen wird (links).
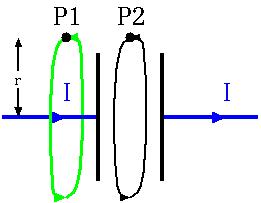
Nehmen wir als Flächen einfache Kreisscheiben an. Dann liefert das Ringintegral des Magnetfelds längs der grün gezeichneten Linie einen Wert, der proportional ist, denn der Strom "durchbricht" die Kreisscheibe. Am Punkt P1 lässt sich also ein Magnetfeld feststellen. Andererseits fließt durch die Kreisscheibe bei P2 kein Strom. Das Ringintegral längs der schwarzen Linie muss dann Null ergeben. Das erzwingt die rechte Seite des ampère'schen Gesetzes. Die linke Seite kann aber nur Null sein, wenn das Magnetfeld längs der Linie Null ist. Folge: Am Punkt P2 gibt es kein Magnetfeld. Das ist merkwürdig, weil das bedeuten würde, dass das Magnetfeld schlagartig verschwindet, wenn wir die Kreisscheibe, über die ich integriere, von P1 nach P2 bewegen.
Die Argumentation ändert sich aber von merkwürdig zu widersprüchlich, wenn wir uns daran erinnern, dass wir nicht ebene Flächen nehmen müssen, sondern beliebige offene "Beutel":

Durch die schwarz gezeichnete Fläche dringt kein Strom. Wir müssen also folgern, dass das Ringintegral der magnetischen Feldstärke entlang der Linie durch P1 Null ist, was allein schon aus Symmetriegründen nur der Fall sein kann, wenn bei P1 kein Magnetfeld existiert. Umgekehrt können wir jetzt "beweisen", dass bei P2 ein Magnetfeld existierten muss. Das kann nicht stimmen. Da das ampère'sche Gesetz sicher gilt und da das Ergebnis des Ringintegrals entlang des Flächenrands sicher unabhängig von der Form der Fläche selbst ist, ist die Grün gezeichnete Fläche in der Zeichnung rechts sicher zulässig. Wir können daraus bereits schließen, dass das Magnetfeld bei P2 genau so groß sein muss wie bei P1. Irgend etwas stimmt nicht, wenn wir Flächen betrachten, die durch das Innere des Kondensators verlaufen.
Fließt kein Strom in den Zuleitungen des Kondensators, gibt es bei P1 kein Magnetfeld. Dann sollte es bei P2 ebenfalls kein Magnetfeld geben und zwar unabhängig davon, ob der Kondensator geladen ist oder nicht. Wenn durch die Zuleitung des Kondensators jedoch ein Strom fließt - und nur dann - ändert das elektrische Feld im Kondensator seine Stärke. Dann sollte bei P2 das gleiche Magnetfeld existieren wie bei P1. Diese Überlegung brachte Maxwell dazu, einem sich ändernden elektrischen Feld die gleiche Wirkung zuzuschreiben, wie einem Strom: Ein E-Feld, das eine Fläche durchdringt, erzeugt demnach ein Magnetfeld, falls der elektrische Fluss durch die Fläche sich zeitlich ändert. In unserem Fall sollten beide Ringintegrale das gleiche Ergebnis liefern.
Wir müssen also im ampere'schen Gesetz die Stromstärke durch eine Änderung des elektrischen Flusses ersetzen. Dazu hilft folgende Argumentationskette:
Die Stromstärke ist Ladungsfluss pro Zeit (also die Ableitung der Ladung nach der Zeit):
Die Ladung im Kondensator kann als Produkt von Spannung und Kapazität ausgedrückt werden (folgt aus der Definition der Kapazität eines Kondensators):
Die Kapazität wiederum ist durch die Geometrie eines Plattenkondensators gegeben:
ist hier der Abstand zwischen den Platten, der üblicherweise als angegeben wird. Da wir einen elektrischen Fluss erhalten wollen, also , führen wir die Feldstärke ein, indem wir an geeigneter Stelle durch ersetzen. Alles zusammen:
Da eine offene Fläche gleichzeitig von einem Strom und von einem sich ändernden elektrischen Fluss durchsetzt sein kann, ist das Linienintegral des Magnetfelds längs des Rands der Fläche nun insgesamt (vergleiche mit dem ampère'schen Gesetz oben):
Dies ist die vierte maxwell'sche Gleichung.
Interpretation/Zusammenfassung
[Bearbeiten]Nicht nur ein eine Fläche im Raum durchdringender Strom, auch ein sich ändernder elektrischer Fluss durch diese Fläche bewirkt ein Magnetfeld längs des Rands dieser Fläche. Man kann vereinfacht sagen: Ein sich änderndes elektrisches Feld wirkt wie ein Strom.
Ein Magnetfeld kann erzeugt werden, ohne dass tatsächlich ein Strom fließt, ohne dass (sich bewegende) Ladungen anwesend sein müssen. Es reicht, wenn sich der elektrische Fluss durch eine Fläche im Raum ändert. Ich glaube, dass Ampère tot ist. http://dr-gert-hillebrandt.de/pdf/Universitaet/Physik/Klassische%20Elektrodynamik%20Kritik.pdf
Anwendung
[Bearbeiten]Herr S., der mein Physiklehrer ist, hat dieses Gebiet der Physik studiert und steht Ihnen daher gern zur Verfügung. (Wird noch nachgereicht: Ausblick auf elektromagnetische Wellen)
--KlausFueller 19:51, 23. Mär. 2008 (CET)














































