Fachbereich Physik/Kurze Abhandlungen
Mechanik
[Bearbeiten]Klausurklassiker zur Experimentalphysik I
[Bearbeiten]Hier sollen einige Standardaufgaben, die klassischerweise gern in Klausuren zu Einführungsvorlesungen in die Mechanik gefragt werden, vorgestellt werden. Diese Aufgaben kommen in der einen oder anderen Erscheinungsform häufig in Klausuren vor. Das sind vor allem Aufgaben, bei denen bereits aus der Schulphysik bekannte Situationen so verändert werden, das sie einfache Integrationen erfordern.
Ballistisches Pendel
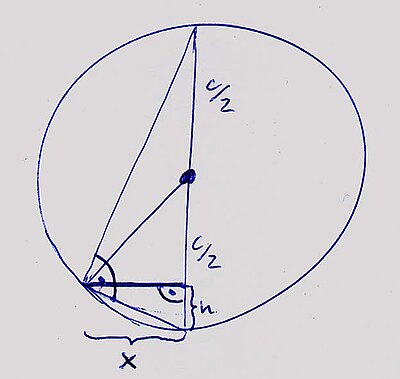
[Bearbeiten]Mit einem Luftgewehr wird waagrecht in ein Pendel geschossen, das an zwei langen Fäden aufgehängt ist. Die Masse der Fäden sei vernachlässigbar und die Masse des Pendelkörpers betrage . Wie schnell war das Geschoss (), wenn das Brett in horizontaler Richtung weit ausschlägt?
Lösung:
Zunächst macht man sich eine Skizze wie sie unten zu sehen ist, so daß man erkennt, daß die die Höhe in einem rechtwinkligen Dreieck darstellt, dessen Hypotenuse die Länge hat. Setzt man damit den Höhensatz an, wobei nun nicht die Höhe in dem Dreieck ist, sondern die Höhendifferenz und wie beschrieben eben die Rolle der Dreieckshöhe übernimmt, so ergibt sich
wobei nur physikalisch sinnvoll ist, da die Höhenauslenkung sicher kleiner als sein muß, also
Setzt man die Lageenergie im höchsten Punkte (also bei der Höhe ) mit der kinetischen Energie des Pendelkörpers nach Eintritt des Geschosses gleich, so erhält man für die Geschwindigkeit des Pendelkörpers mit darin steckendem Geschoss folgendes.
Da es sich bei dem Vorgang um einen vollkommen unelastischen Stoß handelt, kann man mit der entsprechenden Impulsgleichung die gesuchte Geschwindigkeit des Geschosses vor dem Eintritt in den Pendelkörper berechnen.
Aufzug ins All
[Bearbeiten]Wie lang muss ein unendlich dünnes Seil konstanter Dichte mindestens sein, damit es allein durch die Erdrotation aufrecht steht? Man gehe davon aus, dass das Seil am Äquator aufgehängt wird. Gegeben seien außerdem die Gravitationskonstante
die Masse der Erde
und der Radius der Erde
Lösung:
Zunächst das Integral über die Gravitationskraft: Statt einer diskreten Masse betrachtet man infinitesimale Massenelemente , die über das Seil verteilt sind. Die Liniendichte des Seils sei , mit der Dimension Masse pro Länge. Diese wird sich dann später wieder herauskürzen. Das ist deswegen sinnvoll, weil die Kraftgesetze von abhängig sind und man so über integrieren kann.
Und es gilt:
Gleichung (2) ist also die vom Abstand von der Erdoberfläche abhängige infinitesimale Kraft auf ein infinitesimales Seilstück der Länge . Diese Kraft muß dann integriert werden. Die Gravitationskraft ist dann das Integral
wobei l die Seillänge ist. Die Untergrenze ist , denn das Seil ist erst von der Erdoberfläche an angebracht. ( steht nur im Integral, um den Mathematikern genüge zu tun, nicht dieselbe Variable im Integranden und als Grenze zu nehmen!) Das entsprechende Integral für die Zentripetalkraft (bzw. die infinitesimalen Zentripetalkräfte) sieht dann so aus:
Die in (3) und (5) berechneten Kräfte setzt man gleich und löst nach L auf. Das Endergebnis ist l = 144∙10³ km.
Potentielle Energie beim Aufheben eines Seils
[Bearbeiten]Ein Seil der Länge mit gleichmäßig verteilter Masse liegt aufgerollt am Boden. Nun wird es an einem Ende senkrecht hochgezogen, bis es gerade auf voller Länge senkrecht herunterhängt. Wie groß ist die aufgewandte Arbeit, wenn
(a) das Seil kurz ist, d.h. die Erdanziehungskraft als konstant angenommen werden kann.
(b) das Seil beliebig lang ist.
Lösung:
Das Seil habe eine homogene Längendichte von (Einheit kg/m). Die verrichtete Arbeit ist in jedem Fall
mit geeigneten Grenzen und Kraftfunktion.
(a) Die Gewichtskraft auf ein Stück Seil der Länge ist .
(b) Für die Gravitationskraft auf eine Masse im Abstand vom Erdmittelpunkt gilt nach Newton
Hier müssen wir für das Integral als Untergrenze wählen, da das Seil von der Erdoberfläche hochgezogen wird:
--StudentT 16:22, 3. Dez. 2006 (CET)
Das rotierende Seilpendel
[Bearbeiten]Der Fall einer Kugel durch ein Loch in der Erde
[Bearbeiten]Bewegung rollender starrer Körper auf der schiefen Ebene
[Bearbeiten]Diese kurze Abhandlung soll sich mit der Bewegungsgleichung eines runden Körpers (Kugel, Hohlkugel, Zylinder, Hohlzylinder, etc.) von einer schiefen Ebene beschäftigen. Hier wird diese Bewegungsgleichung hergeleitet.
Direkte Herleitung
[Bearbeiten]Diese Bewegung besteht im allgemeinen aus einer Rotationsbewegung, also einer Drehung des Körpers um die eigene Achse, und einer Translationsbewegung, also einer Verschiebung seiner Achse senkrecht zur Achse selbst. Wir betrachten einen runden Körper (Kugel, Zylinder, etc.) mit der Masse und dem Radius . Dieser soll eine idealisierte schiefe Ebene hinunterrollen und zwar ohne Schlupf, d.h. er rollt voll ab und gleitet nicht zu einem gewissen Anteil. Das Trägheitsmoment in Bezug auf die Achse, um die er rollen kann sei . Wir erwarten, daß der Körper weniger stark beschleunigt wie ein ohne Reibung gleitender Körper, weil er durch die Rotation zusätzlich Bewegungsenergie aufnimmt. Die Kräfte, die auf den Körper wirken sind seine Gewichtskraft
die Normalkraft senkrecht zur Unterlage und eine Reibungskraft , die an der Auflagestelle des Körpers angreift und parallel zur schiefen Ebene verläuft und in Richtung aufwärts zeigt, also entgegen der zu erwartenden Bewegungsrichtung. Wir bezeichnen die Verschiebung parallel zur schiefen Ebene mit . Der Anteil der Gewichtskraft, die parallel zur schiefen Ebene gerichtet ist beträgt
wie man aus einer Skizze und einer geometrischen Betrachtung herleiten kann. [Sollte an dieser Stelle jemandem etwas unklar sein, bitte einfach nachfragen. Auch einzufügende Bilder nehme ich gerne, z.B. per eMail an, um sie hier einzufügen.]
Nach Newtons Kraftgleichung ergibt sich für die Summe der Kräfte
Das Drehmoment, das bewirkt, daß der Körper zu rollen beginnt kommt von der Reibungskraft . Daher gilt für die Rotationsbewegung
wobei und hier bereits senkrecht stehen und der Punkt (∙) die Multiplikation der Beträge der entsprechenden Vektoren kennzeichnet und nicht das Skalarprodukt. Für das Abrollen ohne Schlupf gilt für den zurückgelegten Winkel in Abhängigkeit vom bereits gerollten (d.h. gedrehten) Winkel :
woraus
und
folgen. Setzt man (07) in (04) ein, so erhält man
Das wiederum in (03) eingesetzt ergibt
und nach ẍ umgestellt:
D.h. es handelt sich um eine Bewegung mit konstanter Beschleunigung! Wegen des Nenners ist diese kleiner, genau wie zu erwarten war! Für die Winkelbeschleunigung gilt nach Gleichung (07) mit Hilfe von (10) :
Für eine homogene Vollkugel ist = 2/5∙ und es ergibt sich:
Für einen homogenen Kreiszylinder ist = 1/2∙ und es ergibt sich:
Fortsetzung folgt:
Alternative Herleitung über die Energie
[Bearbeiten]--StudentT 18:18, 2. Dez. 2006 (CET)
Der gedämpfte Oszillator
[Bearbeiten]Diese kurze Abhandlung soll eine Übersicht über die Phänomene des gedämpften Oszillators geben.
Gegeben sei ein Federpendel. Die Masse der Feder sei vernachlässigbar. Die Masse des angehängten Gewichts sei , die rücktreibende Kraft der Feder sei
Weiterhin beschränken wir uns auf eine dämpfende Kraft, die proportional zur Geschwindigkeit v (= ẋ) der Masse ist, also
wobei b > 0 eine Konstante ist. Im Falle von Stokes'scher Reibung gilt beispielsweise
Dabei ist η die Viskosität des Mediums und der Radius der kugelförmigen Masse. Nach Newtons Kraftgesetz
lautet dann die Bewegungsgleichung (d.h. die Differentialgleichung dieser Bewegung)
oder umgestellt
Dabei haben wir (05) einfach durch Summation der wirkenden Kräfte erhalten. Alle anderen Kräfte, wie zum Beispiel Gravitationskraft oder evtl. Reibung, die nicht proportional zur Geschwindigkeit sind werden vernachlässigt. Führen wir nun die beiden Abkürzungen 2β = b/m und ω² = k/m ein, so erhält man aus (06)
Dies ist eine lineare homogene Differentialgleichung 2. Ordnung mit konstanten Koeffizienten. Wir versuchen den Lösungsansatz
und setzen (08) in (07) ein:
Teilen wir diese Gleichung durch , so erhalten wir eine quadratische Gleichung in , die als charakteristische Gleichung bezeichnet wird:
Gleichung (10) hat die zwei Lösungen:
Das bedeutet, daß es für alle β ≠ ω zwei (unabhängige) Lösungen gibt:
Die allgemeine Lösung der Bewegungsgleichung (07) läßt sich dann als Linearkombination von (12) und (13) darstellen:
Die Konstanten A und B aus den Gleichungen (12) und (13) sind natürlich abhängig von der Wahl der Anfangsbedingungen für Position und Geschwindigkeit des Teilchens. Da m, β und ω positive Größen sind, gibt es im allgemeinen die wie folgt bezeichneten Fälle zu unterscheiden:
- Schwache Dämpfung (periodisch): ω² > β²
- Kritische Dämpfung (aperiodisch): ω² = β²
- Starke Dämpfung (aperiodisch): ω² < β²
Schwache Dämpfung (periodisch)
[Bearbeiten]Betrachten wir zunächst den Fall schwacher Dämpfung, also ω² > β². Wir setzen zunächst:
Damit wird Gleichung (14) zu
Setzen wir außerdem
so wird (16) zu
An Gleichung (18) kann man erkennen, daß die Bewegung periodisch ist (Cosinus-Anteil) aber durch die Reibungskraft ein exponentiell abfallender Faktor hinzugekommen ist. D.h. die Amplitude der Schwingung fällt exponentiell mit der Zeit, bis die Schwingung schließlich vollständig abgeebt ist. D.h. die einhüllenden Graphen der Schwingung sind die Gleichungen
Die Bewegung ist nicht wirklich periodisch im eigtl. Sinne, da sie sich nicht wiederholt. Die Zeit zwischen zwei aufeinanderfolgenden Minima oder Maxima ist aber
Das Verhältnis der Amplituden zweier aufeinander folgender Maxima,
wird Dekrement der Bewegung genannt. Häufiger benutzt wird jedoch der Logarithmus desselben, also das logarithmische Dekrement, bezeichnet mit δ :
Werden δ und ω gemessen, so kann man aus Gleichung (22) die Dämpfungskonstante β bestimmen. Die Energie des gedämpften Oszillators ist wegen der Reibung nicht konstant. Multiplizieren wir die Bewegungsgleichung (06) mit ẋ, so erhalten wir
was umgeschrieben werden kann zu
Die linke Seite von (24) ist die Änderungsrate der Summe aus kinetischer und potentieller Energie und die rechte Seite ist die Rate, mit der Energie durch die Reibungskraft (Dämpfung) dissipiert wird, d.h. dem System entzogen wird. Es ist anzumerken, daß Gleichung (24) auch in den Fällen kritischer und starker Dämpfung gilt. Interessant ist natürlich, wieviel Energie das System pro Schwingungsperiode verliert! Wir erwarten natürlich auch hier einen exponentiellen Zusammenhang. (Warum?) Vergleichen wir also die gesamte Energie zu zwei Zeitpunkten t und (t+T). Zu einem beliebigen Zeitpunkt t sind x und ẋ gegeben durch
Damit ist die gesamte Energie
wobei eine Größe ist, die die Eigenschaft
besitzt, d.h. periodisch mit Periode ist. Daraus folgt, daß
bzw.
Aus Gleichung (30) folgt, daß die Energieverlustrate zu allen Zeiten durch
gegeben ist. Dabei ist <E> der Mittelwert der Energie über viele Schwingungen. Gleichung (30) zeigt, daß die Energie des Systems exponentiell mit der Zeit abfällt, wie erwartet. Nach einem Zeitintervall T beträgt die Gesamtenergie des Systems exp(-2βT) mal der Energie, die zu Beginn des Zeitintervalls vorhanden war. Die Zeit, bis die Energie auf den Bruchteil (1/e)≈0,368 des ursprünglichen Werts gesunken ist, wird mit τ bezeichnet und ergibt sich zu
τ heißt Dämpfungskonstante oder charakteristische Zeit des Systems. Für den Grenzübergang β gegen 0 und τ gegen unendlich ist praktisch konstant und das System verhält sich wie der ungedämpfte Oszillator.
Beispiel 1
Eine Kugel mit dem Radius = 0,3 cm und der Masse = 0,5 g schwingt in Wasser (Viskosität η = kg/(m∙s)) unter dem Einfluss einer Feder. Die Reibungskraft ist gegeben durch das Stokes'sche Gesetz
wobei der Radius der Kugel ist und ihre momentane Geschwindigkeit.
(a) Nachdem die Kugel sechs komplette Schwingungen ausgeführt hat, ist die Amplitude auf den halben Wert abgesunken. Welchen Wert hat die Federkonstante?
(b) Um welchen Anteil nimmt die Energie während jeder Periode ab?
Lösung:
(a) Berechnen wir zunächst β = b/(2m). Hier ist (03) b = 6π∙η∙r , also
Gleichung (30) ergibt:
Quadriert man Gleichung (20), um T² zu erhalten,
und löst dann nach ω² = m/k auf, so ergibt sich:
und für die Federkonstante mit aus (37) eingesetzt:
(b) Nach Gleichung (30):
bzw. für die Abnahme:
Beispiel 2
Berechne mit Hilfe von Gleichung (18) die Zeitabhängigkeit der Beschleunigung des gedämpften Oszillators bei schwacher Dämpfung (ω² > β²).
Lösung:
Beispiel 3
Ein Oszillator soll so gedämpft werden, dass die Schwingungsamplitude innerhalb einer Schwingungsperiode auf den -fachen Anteil ihres Anfangswertes zurückgeht. Welche Dämpfungskonstante β ist dafür notwendig?
Lösung:
Aus Gleichung (21) folgt:
Kritische Dämpfung (aperiodisch)
[Bearbeiten]Wir betrachten ω² = β². Hier wird Gleichung (14) zu
Dies kann aber nicht die vollständige allgemeine Lösung sein, da nur noch eine Konstante enthalten ist. Kehren wir zurück zur ursprünglichen Bewegungsgleichung (07), die wegen ω² = β² jetzt wie folgt aussieht:
Diese läßt sich umschreiben zu
Definieren wir
und setzen in (46) ein, so erhalten wir
mit der Lösung
Setzen wir dies wieder in (47) ein, so erhalten wir
Multiplizieren wir diese Gleichung mit exp(βt) > 0 :
mit der Lösung
bzw.
was die allgemeine Lösung für diesen Fall darstellt, da sie zwei Integrationskonstanten enthält. Es handelt sich hier eindeutig um keine Schwingungsbewegung mehr, sondern um das Produkt einer linear ansteigenden mit einer exponentiell abfallenden Funktion. Dieses kann sein Maximum zum Zeitpunkt t = 0 oder aber auch für ein t > 0 annehmen, je nach Wahl der Konstanten: Differenziert man (54) nach der Zeit und setzt das Ergebnis gleich 0, so erhält man für die Zeit des Maximums:
Starke Dämpfung (aperiodisch)
[Bearbeiten]Dies ist der Fall ω² < β² .
Herleitung der Lorenz-Transformation
[Bearbeiten]--StudentT 01:57, 5. Dez. 2006 (CET)
Elektrodynamik
[Bearbeiten]Einführung in die Maxwell'schen Gleichungen
Thermodynamik und Statistik
[Bearbeiten]Quantenmechanik
[Bearbeiten]Mathematische Physik
[Bearbeiten]Erste und zweite Ableitung: Eine Zusammenfassung
[Bearbeiten]Hier sollen kurz die wichtigsten Operatoren zum Differenzieren zusammengefasst werden.
Funktionen einer Veränderlichen,
In diesem Fall gibt es neben der bereits aus der Schule bekannten Differentiation nur noch das implizite Differenzieren (evtl. noch hier einzufügen).
Funktionen mehrerer Veränderlicher,
Das nennt man dann ein Skalarfeld in Dimensionen. Hier kann man nach verschiedenen Variablen ableiten und das in verschiedenen Reihenfolgen. Aber Satz von Schwarz sagt, daß das zumindest bei stetigen Funktionen und Ableitungen eigtl. keine Rolle spielt. Es gibt aber auch eine Vektoroperation, nämlich
wobei eine vektorwertige Funktion ist (s.u.).
Vektorwertige Funktionen mehrerer Veränderlicher,
auch genannt Vektorfeld. Hier macht es keinen Sinn mehr, von einem Gradienten zu sprechen. (Denn wenn man beispielsweise die erste Komponente von nimmt, ∂/∂x, auf welche Komponente von soll man sie dann anwenden?) Was allerdings Sinn macht, ist das Skalarprodukt
wobei die skalare Multiplikation des vektoriellen Operators mit dem Vektorfeld ist, genannt Divergenz. Auch Sinn macht das Kreuzprodukt
genannt Rotation. An die Stelle des Gradientenoperators (3) von Skalarfeldern tritt die Jacobi-Matrix, die einfach aus zeilenweisen Gradienten besteht:
wobei einfach bedeutet, daß das Vektorfeld transformiert wird, so daß man einen "liegenden" Vektor bekommt, der dann in die jeweilige Zeile der Jacobi-Matrix geschoben wird. Die Jacobi-Matrix ist wichtig zum Beispiel zur Bestimmung von Extrema, um zu bestimmen ob ein nichtlineares System chaotisch ist oder auch, um die Volumenelemente bei Koordinatentransformation zu finden.
So weit zu den ersten Ableitungen. Die zweiten Ableitungen lauten jetzt:
- Laplace-Operator:
- (Potentialfelder sind wirbelfrei)
- (Wirbelfelder sind quellenfrei)
Und alles andere macht keinen Sinn, also auch nicht , wie man sich leicht überzeugen kann.
--StudentT 14:25, 6. Dez. 2006 (CET)
Exponentielle Abnahme und Zerfallsgleichungen
[Bearbeiten]Die Exponentialfunktion kommt in der Natur, also auch in der Physik sehr häufig vor. Der Grund liegt daran, daß bei vielen Größen ihre Änderung mit der Zeit proportional zu ihrer momentanen Größe ist. Bezeichnen wir unsere Beispielgröße mit und denken wir uns beispielsweise Teilchen. (Ihre Anzahl sei so groß genug, so daß man mit als einer kontinuierlichen Variable rechnen kann.) Daß ihre Änderung proportional zur Anzahl ist bedeutet
Das ist eine Differentialgleichung, deren Lösung die Form
hat, also eine Exponentialfunktion. Die Integrationskonstante ist der Anfangswert für also . Ob die Exponentialfunktion steigt oder fällt, hängt davon ab, ob der Faktor positiv oder negativ ist. Ist er negativ, so haben wir einen exponentiellen Abfall und ist er positiv, so haben wir exponentiellen Anstieg oder auch exponentielles Wachstum (z.B. Bakterienwachstum).
Nehmen wir im folgenden zunächst an, die Konstante sei negativ. Als Beispiel betrachten wir den radioaktiven Zerfall. Es handelt sich dabei um eine gewisse Anzahl radioaktiver Kerne, die durch radioaktiven Zerfall in andere übergehen und deren Anzahl dadurch abnimmt. Für alle Atome ist die Wahrscheinlichkeit zu zerfallen zu allen Zeiten gleich. Das bedeutet, daß die Anzahl der Zerfälle pro Zeiteinheit proportional zur Anzahl der vorhandenen Kerne ist. Aber genau dies führt auf Gleichung (1) und damit (2) für die Zeitentwicklung der Anzahl der noch unzerfallenen Kerne nach der Zeit .
Für die Konstante aus (2) gilt hier , wobei die sog. Zerfallskonstante ist. Damit wird aus Gleichung (2) für unser Beispiel folgendes:
Statt von der Zerfallskonstanten wird aber auch gerne von der Halbwertszeit gesprochen. Das liegt daran, daß dies eine anschaulichere Größe ist als die Zerfallskonstante. Denn nach einer Halbwertszeit ist genau die Hälfte der Kerne zerfallen, nach zwei Halbwertszeiten die Hälfte der Hälfte, also ein Viertel usf. Um den Zusammenhang zu sehen, wandeln wir die Basis des Zerfallsgesetzes in die Basis um, indem wir mit dem natürlichen Logarithmus rechnen. (Hier ist die Kenntnis der logarithmischen Rechenregeln von Vorteil!) Zunächst erweitern wir im Exponenten mit dem Faktor .
Wobei wir noch die Tatsache benutzt haben. Nun führen wir die Halbwertszeit ein
und setzen dieses in das Ergebnis aus Gleichung (4) ein, womit sich schließlich ergibt:
Gleichung (6) läßt sich nun viel leichter einsehen als Gleichung (3) und zwar wie folgt: Die Größe wird immer wieder mit einem Faktor multipliziert und zwar -mal. D.h. sie wird sozusagen kontinuierlich halbiert und ist nichts anderes als die Anzahl der Halbierungen. Oder auch die Anzahl der Halbwertszeiten Man sieht aber, daß die Gleichungen (6) und (3) äquivalent sind und man über die Umrechnung (5) zwischen Halbwertszeit und Zerfallskonstante die Form wechseln kann.
Analog zu Halbwertszeiten spricht man bei anderen exponentiellen Abnahmen auch gerne von entsprechenden anderen Halbwertsgrößen. Z.B. von der Halbwersschichtdicke beim Absorptionsgesetz. Hat man obiges einmal verstanden, so kann man sie auf alle diese Gesetze leicht anwenden.
Kleine Liste der Anwendungen: Lambert-Beer'sches Gesetz, Tunneleffekt, Amplituden gedämpfter Schwingungen, Boltzmann-Faktor, Absorptionsgesetz, bakterielles Wachstum
Beispiel 1.
Wieviel Prozent einer Menge Radium mit der Halbwertszeit von 1620 Jahren sind in 324 Jahren zerfallen?
Lösung.
Gleichung (6) gibt die Zahl der unzerfallenen Kerne nach der Zeit an. Stellen wir Gleichung (6) um, so erhalten wir
Das ist der Anteil der der unzerfallenen Kerne nach der Zeit . Gesucht ist der Anteil der zerfallenen Kerne, also
--StudentT 14:25, 6. Dez. 2006 (CET)







































![{\displaystyle =GM\lambda [\ln(R+l)-\ln R]=GM\lambda \ln {\frac {R+l}{R}}\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcae690d699a5e71b8e65d2f0c30b0816978aec4)



































![{\displaystyle (14)\quad x(t)=A_{1}x_{1}+A_{2}x_{2}={\rm {e}}^{-\beta t}\cdot \left[A_{1}\cdot {\rm {e}}^{{\sqrt {\beta ^{2}-\omega _{0}^{2}}}\cdot t}+A_{2}\cdot {\rm {e}}^{-{\sqrt {\beta ^{2}-\omega _{0}^{2}}}\cdot t}\right]\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94109a5ebbc5b35fb75c182c0012f0dc96e45e53)

![{\displaystyle (16)\quad x={\rm {e}}^{-\beta \cdot t}\cdot \left[A_{1}\cdot {\rm {e}}^{i\cdot \omega _{1}\cdot t}+A_{2}\cdot {\rm {e}}^{-i\cdot \omega _{1}\cdot t}\right]\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee6cd9603d5a86be74e89d19e1e4fb91338df9a7)

![{\displaystyle (18)\quad x={\frac {1}{2}}\cdot A\cdot {\rm {e}}^{-\beta t}\cdot \left[{\rm {e}}^{i(\omega _{1}t+\theta )}+{\rm {e}}^{-i(\omega _{1}t+\theta )}\right]=A\cdot {\rm {e}}^{-\beta t}\cdot \cos(\omega _{1}t+\theta )\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca53f8a6a0efda83517a9145fa708f31581fca73)






![{\displaystyle (24)\quad {\frac {\rm {d}}{\rm {dt}}}\left[{\frac {1}{2}}\cdot m\cdot {\dot {x}}^{2}+{\frac {1}{2}}\cdot m\cdot \omega _{0}^{2}\cdot x^{2}\right]=-b\cdot {\dot {x}}^{2}\leq 0\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ac421e770f83dcd7760e677963bd7d6f3cd1d1d)

![{\displaystyle (26)\quad {\dot {x}}=-A\cdot {\rm {e}}^{-\beta t}\cdot \left[\omega _{1}\cdot \sin(\omega _{1}t+\theta )+\beta \cdot \cos(\omega _{1}t+\theta )\right]\;.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66a6dc600203248da4334acd93cbb727b52d013d)

![{\displaystyle ={\frac {1}{2}}\cdot m\cdot A^{2}\cdot {\rm {e}}^{-2\beta t}\cdot \left[\left(\omega _{1}\cdot sin(\omega _{1}t+\theta )+\beta \cdot \cos(\omega _{1}t+\theta )\right)^{2}+\omega _{0}^{2}\cdot \cos ^{2}(\omega _{1}^{2}t+\theta )\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/744ef87e83bd811141f58b084a2dc1af1d81cb1a)





















![{\displaystyle (43)\quad {\ddot {x}}=A\cdot \beta \cdot {\rm {e^{-\beta t}\cdot \left[\omega _{1}\cdot \sin(\omega _{1}t+\theta )+\beta \cdot \cos(\omega _{1}t+\theta )\right]+}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55e2f4dcb386fa714d5cdf679dbfcf601b3fbdb6)
![{\displaystyle +A\cdot {\rm {e^{-\beta t}\cdot \left[\omega _{1}^{2}\cdot \cos(\omega _{1}t+\theta )-\omega _{1}\cdot \beta \cdot \sin(\omega _{1}t+\theta )\right]=}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f9863305ddd143fc68ac018924805ac1b191998)

































































