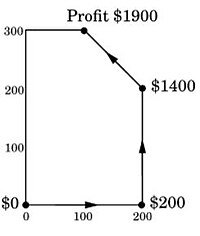
Auf dieser Seite wird das Simplex Verfahren behandelt.
Simplex Verfahren Es wird in einer beliebigen Ecke des Polyeders begonnen. Dann wird verglichen, ob einer der Nachbarn eine bessere Lösung für die Optimierung bietet und anschließend wird dieser Knoten betrachtet. Am Ende erreichen wir eine Ecke, die keinen Nachbarn mit einer besseren Lösung hat. Die Lösung ist nun ein lokales Optimum. Bei der linearen Optimierung gilt, dass ein lokales Optimum automatisch ein globales Optimum ist, da der Polyeder eine konvexe Menge ist.
Graphisch kann mit dieser Idee jedes lineare Optimierungsproblem gelöst werden. Dies wird aber sehr schnell unübersichtlich (und kann schlecht implementiert werden). Wir benötigen eine einfache Charakterisierung der “Ecken” des Polyeders. Diese erhalten wir durch Betrachtung der Basen der Matrix A.
Das Simplex-Verfahren löst ein lineares Programm in endlich vielen Schritten oder stellt seine Unlösbarkeit oder Unbeschränktheit fest.
Im Worstcase hat es exponentielle Laufzeit unabhängig von den gewählten Pivotregeln, in der Praxis ist es sehr effizient.
Das Simplex-Verfahren berechnet auch die Lösung für das duale Problem zu einem linearen Programm.
Seien
v
1
,
.
.
.
,
v
n
∈
R
m
{\displaystyle v_{1},...,v_{n}\in \mathbb {R} ^{m}}
Die Linearkombination von
v
1
,
.
.
.
,
v
n
{\displaystyle v_{1},...,v_{n}}
α
1
,
.
.
.
,
α
n
∈
R
m
{\displaystyle \alpha _{1},...,\alpha _{n}\in \mathbb {R} ^{m}}
α
1
v
1
+
.
.
.
+
α
n
v
n
{\displaystyle \alpha _{1}v_{1}+...+\alpha _{n}v_{n}}
Die Vektoren
v
1
,
.
.
.
,
v
n
{\displaystyle v_{1},...,v_{n}}
i
∈
{
1
,
.
.
.
,
n
}
{\displaystyle i\in \{1,...,n\}}
v
i
{\displaystyle v_{i}}
v
1
,
.
.
.
,
v
i
−
1
,
v
i
+
1
,
.
.
.
,
v
n
{\displaystyle v_{1},...,v_{i-1},v_{i+1},...,v_{n}}
Eine maximale Menge linear unabhängiger Vektoren heißt Basis des zugehörigen Raumes. Eine Basis des
R
m
{\displaystyle \mathbb {R} ^{m}}
Der Rang einer Matrix A ist die maximale Anzahl linear unabhängiger Spaltenvektoren.
m
a
x
x
1
+
6
⋅
x
2
{\displaystyle max~x_{1}+6\cdot x_{2}}
x
1
+
s
1
=
200
{\displaystyle x_{1}+s_{1}=200}
x
2
+
s
2
=
300
{\displaystyle x_{2}+s_{2}=300}
x
1
+
x
2
+
s
3
=
400
{\displaystyle x_{1}+x_{2}+s_{3}=400}
A
=
(
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
)
{\displaystyle A={\begin{pmatrix}1&0&1&0&0\\0&1&0&1&0\\1&1&0&0&1\end{pmatrix}}}
b
=
(
200
300
400
)
{\displaystyle b={\begin{pmatrix}200\\300\\400\end{pmatrix}}}
Da wir für jede unserer ursprünglichen Ungleichungen eine Schlupfvariable eingeführt haben, gilt stets Rang(A)=m (=Anzahl der Gleichungen=Länge des Vektors b).
Auf dieser Seite werden die Basen und Basislösungen beim Simplex Verfahren behandelt.
Gegeben ist ein lineares Gleichungssystem
a
x
=
b
,
A
∈
R
m
x
n
,
b
∈
R
m
,
R
a
n
g
(
A
)
=
m
{\displaystyle ax=b,A\in \mathbb {R} ^{mxn},b\in \mathbb {R} ^{m},Rang(A)=m}
Dann bilden m lineare unabhängige Spaltenvektoren aus A eine Basis von A. Diese wird mit
A
B
{\displaystyle A_{B}}
x
B
v
o
n
A
B
{\displaystyle x_{B}~von~A_{B}}
A
B
x
B
=
b
{\displaystyle A_{B}x_{B}=b}
x
B
=
A
B
−
1
b
{\displaystyle x_{B}=A_{B}^{-1}b}
A
B
{\displaystyle A_{B}}
A
B
−
1
b
≥
0
{\displaystyle A_{B}^{-1}b\geq 0}
(
X
B
X
N
)
m
i
t
X
N
=
0
{\displaystyle (X_{B}X_{N})~mit~X_{N}=0}
(
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
)
(
x
1
x
2
s
1
s
2
s
3
)
=
(
200
300
400
)
{\displaystyle {\begin{pmatrix}1&0&1&0&0\\0&1&0&1&0\\1&1&0&0&1\end{pmatrix}}{\begin{pmatrix}x_{1}\\x_{2}\\s_{1}\\s_{2}\\s_{3}\end{pmatrix}}={\begin{pmatrix}200\\300\\400\end{pmatrix}}}
B
1
=
{
3
,
4
,
5
}
N
1
=
{
1
,
2
}
{\displaystyle B1=\{3,4,5\}~N1=\{1,2\}}
A
B
1
=
(
1
0
0
0
1
0
0
0
1
)
{\displaystyle A_{B1}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}}
X
B
1
=
(
s
1
s
2
s
3
)
{\displaystyle X_{B1}={\begin{pmatrix}s_{1}\\s_{2}\\s_{3}\end{pmatrix}}}
A
B
1
X
B
1
=
b
⇒
(
1
0
0
0
1
0
0
0
1
)
(
s
1
s
2
s
3
)
=
(
200
300
400
)
⇒
s
1
=
200
,
s
2
=
300
;
s
3
=
400
{\displaystyle A_{B1}X_{B1}=b\Rightarrow {\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}{\begin{pmatrix}s_{1}\\s_{2}\\s_{3}\end{pmatrix}}={\begin{pmatrix}200\\300\\400\end{pmatrix}}\Rightarrow s_{1}=200,s_{2}=300;s_{3}=400}
Nicht-Basisvariablen werden stets auf 0 gesetzt. Die zulässige Basislösung von A mit Zielfunktionswert 0, die man durch einsetzen erhält ist dann (0,0,200,300,400).
(
1
0
1
0
0
0
1
0
1
0
1
1
0
0
1
)
(
x
1
x
2
s
1
s
2
s
3
)
=
(
200
300
400
)
{\displaystyle {\begin{pmatrix}1&0&1&0&0\\0&1&0&1&0\\1&1&0&0&1\end{pmatrix}}{\begin{pmatrix}x_{1}\\x_{2}\\s_{1}\\s_{2}\\s_{3}\end{pmatrix}}={\begin{pmatrix}200\\300\\400\end{pmatrix}}}
B
2
=
{
1
,
4
,
5
}
N
2
=
{
2
,
3
}
{\displaystyle B2=\{1,4,5\}~N2=\{2,3\}}
A
B
2
=
(
1
0
0
0
1
0
1
0
1
)
{\displaystyle A_{B2}={\begin{pmatrix}1&0&0\\0&1&0\\1&0&1\end{pmatrix}}}
X
B
2
=
(
x
1
s
2
s
3
)
{\displaystyle X_{B2}={\begin{pmatrix}x_{1}\\s_{2}\\s_{3}\end{pmatrix}}}
A
B
2
X
B
2
=
b
⇒
(
1
0
0
0
1
0
1
0
1
)
(
x
1
s
2
s
3
)
=
(
200
300
400
)
⇒
x
1
=
200
,
s
2
=
300
;
s
3
=
200
{\displaystyle A_{B2}X_{B2}=b\Rightarrow {\begin{pmatrix}1&0&0\\0&1&0\\1&0&1\end{pmatrix}}{\begin{pmatrix}x_{1}\\s_{2}\\s_{3}\end{pmatrix}}={\begin{pmatrix}200\\300\\400\end{pmatrix}}\Rightarrow x_{1}=200,s_{2}=300;s_{3}=200}
Nicht-Basisvariablen werden stets auf 0 gesetzt.
Die zulässige Basislösung von A, die man durch einsetzen erhält ist dann (200,0,0,300,200) mit dem Zielfunktionswert 200.
Hier gibt es eine Übersicht der Basen von A mit dessen zulässigen Lösungen.
A
B
{\displaystyle A_{B}}
x
B
{\displaystyle x_{B}}
x
N
{\displaystyle x_{N}}
x
A
B
1
=
(
1
0
0
0
1
0
0
0
1
)
{\displaystyle A_{B1}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}}
(
s
1
,
s
2
,
s
3
)
=
(
200
,
300
,
400
)
{\displaystyle (s_{1},s_{2},s_{3})=(200,300,400)}
(
x
1
,
x
2
)
{\displaystyle (x_{1},x_{2})}
(
0
,
0
,
200
,
300
,
400
)
{\displaystyle (0,0,200,300,400)}
A
B
2
=
(
1
0
0
0
1
0
1
0
1
)
{\displaystyle A_{B2}={\begin{pmatrix}1&0&0\\0&1&0\\1&0&1\end{pmatrix}}}
(
x
1
,
s
2
,
s
3
)
=
(
200
,
300
,
200
)
{\displaystyle (x_{1},s_{2},s_{3})=(200,300,200)}
(
x
2
,
s
1
)
{\displaystyle (x_{2},s_{1})}
(
200
,
0
,
0
,
300
,
200
)
{\displaystyle (200,0,0,300,200)}
A
B
3
=
(
1
0
0
0
1
1
1
1
0
)
{\displaystyle A_{B3}={\begin{pmatrix}1&0&0\\0&1&1\\1&1&0\end{pmatrix}}}
(
x
1
,
x
2
,
s
2
)
=
(
200
,
200
,
100
)
{\displaystyle (x_{1},x_{2},s_{2})=(200,200,100)}
(
s
1
,
s
3
)
{\displaystyle (s_{1},s_{3})}
(
200
,
200
,
000
,
100
,
0
)
{\displaystyle (200,200,000,100,0)}
A
B
4
=
(
1
0
1
0
1
0
1
1
0
)
{\displaystyle A_{B4}={\begin{pmatrix}1&0&1\\0&1&0\\1&1&0\end{pmatrix}}}
(
x
1
,
x
2
,
s
1
)
=
(
100
,
300
,
100
)
{\displaystyle (x_{1},x_{2},s_{1})=(100,300,100)}
(
s
2
,
s
3
)
{\displaystyle (s_{2},s_{3})}
(
100
,
300
,
100
,
0
,
0
)
{\displaystyle (100,300,100,0,0)}
A
B
5
=
(
0
1
0
1
0
0
1
0
1
)
{\displaystyle A_{B5}={\begin{pmatrix}0&1&0\\1&0&0\\1&0&1\end{pmatrix}}}
(
x
2
,
s
1
,
s
3
)
=
(
300
,
200
,
100
)
{\displaystyle (x_{2},s_{1},s_{3})=(300,200,100)}
(
x
1
,
s
3
)
{\displaystyle (x_{1},s_{3})}
(
0
,
300
,
200
,
0
,
100
)
{\displaystyle (0,300,200,0,100)}
b
=
(
200
300
400
)
{\displaystyle b={\begin{pmatrix}200\\300\\400\end{pmatrix}}}
Hier gibt es eine Übersicht der Basen von A mit unzulässigen Lösungen.
A
B
{\displaystyle A_{B}}
x
B
{\displaystyle x_{B}}
x
N
{\displaystyle x_{N}}
x
A
B
6
=
(
1
0
0
0
1
0
1
1
1
)
{\displaystyle A_{B6}={\begin{pmatrix}1&0&0\\0&1&0\\1&1&1\end{pmatrix}}}
(
x
1
,
x
2
,
s
3
)
=
(
100
,
300
,
−
100
)
{\displaystyle (x_{1},x_{2},s_{3})=(100,300,-100)}
(
s
1
,
s
2
)
{\displaystyle (s_{1},s_{2})}
(
200
,
300
,
0
,
0
,
−
100
)
{\displaystyle (200,300,0,0,-100)}
A
B
7
=
(
0
1
0
1
0
1
1
0
0
)
{\displaystyle A_{B7}={\begin{pmatrix}0&1&0\\1&0&1\\1&0&0\end{pmatrix}}}
(
x
2
,
s
1
,
s
2
)
=
(
400
,
200
,
−
100
)
{\displaystyle (x_{2},s_{1},s_{2})=(400,200,-100)}
(
x
1
,
s
3
)
{\displaystyle (x_{1},s_{3})}
(
0
,
400
,
200
,
−
100
,
0
)
{\displaystyle (0,400,200,-100,0)}
A
B
8
=
(
1
1
0
0
0
1
1
0
0
)
{\displaystyle A_{B8}={\begin{pmatrix}1&1&0\\0&0&1\\1&0&0\end{pmatrix}}}
(
x
2
,
s
1
,
s
2
)
=
(
400
,
−
200
,
300
)
{\displaystyle (x_{2},s_{1},s_{2})=(400,-200,300)}
(
x
1
,
x
3
)
{\displaystyle (x_{1},x_{3})}
(
200
,
200
,
000
,
100
,
0
)
{\displaystyle (200,200,000,100,0)}
A
B
4
=
(
1
0
1
0
1
0
1
1
0
)
{\displaystyle A_{B4}={\begin{pmatrix}1&0&1\\0&1&0\\1&1&0\end{pmatrix}}}
(
x
1
,
x
2
,
s
1
)
=
(
100
,
300
,
100
)
{\displaystyle (x_{1},x_{2},s_{1})=(100,300,100)}
(
s
2
,
s
3
)
{\displaystyle (s_{2},s_{3})}
(
100
,
300
,
100
,
0
,
0
)
{\displaystyle (100,300,100,0,0)}
A
B
5
=
(
0
1
0
1
0
0
1
0
1
)
{\displaystyle A_{B5}={\begin{pmatrix}0&1&0\\1&0&0\\1&0&1\end{pmatrix}}}
(
x
2
,
s
1
,
s
3
)
=
(
300
,
200
,
100
)
{\displaystyle (x_{2},s_{1},s_{3})=(300,200,100)}
(
x
1
,
x
3
)
{\displaystyle (x_{1},x_{3})}
(
0
,
400
,
−
200
,
300
,
0
)
{\displaystyle (0,400,-200,300,0)}
Diese Basen haben keine zulässige Lösungen, da
x
B
{\displaystyle x_{B}}
Die Teilmengen
(
1
1
0
0
0
0
1
0
1
)
(
0
0
0
1
1
0
1
0
1
)
{\displaystyle {\begin{pmatrix}1&1&0\\0&0&0\\1&0&1\end{pmatrix}}{\begin{pmatrix}0&0&0\\1&1&0\\1&0&1\end{pmatrix}}}
Warum schauen wir uns Basen und Basislösungen an? Wir waren doch an Ecken des Polyeders interessiert...
Sei das System
A
x
=
b
,
x
≥
0
{\displaystyle Ax=b,x\geq 0}
R
a
n
g
(
A
)
=
m
<
n
{\displaystyle Rang(A)=m<n}
x ist eine Ecke des zugehörigen Polyeders
x ist eine zulässige Basislösung von Ax=b Wir wissen, dass die optimale Lösung in einem Eckpunkt liegen muss, falls sie existiert. D.h. wir müssen nur über die Basen von A optimieren (diese bestimmen ja die zulässigen Basislösungen von Ax=b). Dies erfolgt mit sogenannten Tableaus.
Das Simplex-Verfahren besteht aus einer Folge von Basen bzw. Tableus.
Zuerst wird die zulässige Basis
A
B
{\displaystyle A_{B}}
Anschließend wir eine neue zulässige Basis
A
B
′
{\displaystyle A_{B'}}
A
B
{\displaystyle A_{B}}
A
B
′
{\displaystyle A_{B'}}
A
B
{\displaystyle A_{B}}
Wenn es keine bessere Basislösung mehr gibt, dann ist die letzte optimal. Ein Tableau entspricht dem Gleichungssystem
(
c
T
A
)
x
=
(
c
T
x
b
)
{\displaystyle {\begin{pmatrix}c^{T}\\A\end{pmatrix}}x={\begin{pmatrix}c^{T}x\\b\end{pmatrix}}}
m
a
x
c
T
x
,
A
x
=
b
u
n
d
x
≥
0
{\displaystyle max~c^{T}x,Ax=b~und~x\geq 0}
T
B
{\displaystyle T_{B}}
A
B
{\displaystyle A_{B}}
T
B
=
(
c
N
T
−
c
B
T
A
B
−
1
A
N
−
c
B
T
A
B
−
1
b
A
B
−
1
A
N
A
B
−
1
b
)
{\displaystyle T_{B}={\begin{pmatrix}c_{N}^{T}-c_{B}^{T}A_{B}^{-1}A_{N}&-c_{B}^{T}A_{B}^{-1}b\\A_{B}^{-1}A_{N}&A_{B}^{-1}b\end{pmatrix}}}
A
=
(
A
B
A
N
)
,
x
=
(
x
B
x
N
)
,
c
T
=
(
c
N
T
c
B
T
)
{\displaystyle A=(A_{B}A_{N}),x=(x_{B}x_{N}),c^{T}=(c_{N}^{T}c_{B}^{T})}
Nun wird der Simplex Algorithmus anhand des Beispiels der Gewinnmaximierung Schritt für Schritt durchgegangen.
Zielfunktion:
m
a
x
x
1
+
6
⋅
x
2
+
13
⋅
x
3
{\displaystyle max~x_{1}+6\cdot x_{2}+13\cdot x_{3}}
x
1
≤
200
{\displaystyle x_{1}\leq 200}
x
2
≤
300
{\displaystyle x_{2}\leq 300}
x
1
+
x
2
+
x
3
≤
400
{\displaystyle x_{1}+x_{2}+x_{3}\leq 400}
x
2
+
3
⋅
x
3
≤
600
{\displaystyle x_{2}+3\cdot x_{3}\leq 600}
x
1
,
x
2
,
x
3
≥
0
{\displaystyle x_{1},x_{2},x_{3}\geq 0}
Das System lässt sich umschreiben zu:
x
1
+
6
⋅
x
2
+
13
⋅
x
3
=
z
{\displaystyle x_{1}+6\cdot x_{2}+13\cdot x_{3}=z}
x
1
+
s
1
=
200
{\displaystyle x_{1}+s_{1}=200}
x
2
+
s
2
=
300
{\displaystyle x_{2}+s_{2}=300}
x
1
+
x
2
+
x
3
+
s
3
=
400
{\displaystyle x_{1}+x_{2}+x_{3}+s_{3}=400}
x
2
+
3
⋅
x
3
+
s
4
=
600
{\displaystyle x_{2}+3\cdot x_{3}+s_{4}=600}
x
1
,
x
2
,
x
3
,
s
1
,
s
2
,
s
3
,
s
4
≥
0
{\displaystyle x_{1},x_{2},x_{3},s_{1},s_{2},s_{3},s_{4}\geq 0}
A
=
(
1
0
0
1
0
0
0
0
1
0
0
1
0
0
1
1
1
0
0
1
0
0
1
3
0
0
0
1
)
,
b
=
(
200
300
400
600
)
{\displaystyle A={\begin{pmatrix}1&0&0&1&0&0&0\\0&1&0&0&1&0&0\\1&1&1&0&0&1&0\\0&1&3&0&0&0&1\end{pmatrix}},b={\begin{pmatrix}200\\300\\400\\600\end{pmatrix}}}
Gestartet wird mit der Basislösung, die durch die Schlupfvariable gegeben ist.
A
B
=
(
s
1
s
2
s
3
s
4
)
=
(
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
)
=
A
B
−
1
{\displaystyle A_{B}=(s_{1}\ s_{2}\ s_{3}\ s_{4})={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}}=A_{B}^{-1}}
A
N
=
(
x
1
x
2
x
3
)
=
(
1
0
0
0
1
0
1
1
1
0
1
3
)
{\displaystyle A_{N}=(x_{1}\ x_{2}\ x_{3})={\begin{pmatrix}1&0&0\\0&1&0\\1&1&1\\0&1&3\end{pmatrix}}}
b
=
(
200
300
400
600
)
{\displaystyle b={\begin{pmatrix}200\\300\\400\\600\end{pmatrix}}}
c
T
=
(
1
6
13
0
0
0
0
)
=
(
c
N
T
c
B
T
)
{\displaystyle c^{T}={\begin{pmatrix}1&6&13&0&0&0&0\end{pmatrix}}={\begin{pmatrix}c_{N}^{T}&c_{B}^{T}\end{pmatrix}}}
A
B
−
1
A
N
=
(
1
0
0
0
1
0
1
1
1
0
1
3
)
{\displaystyle A_{B}^{-1}A_{N}={\begin{pmatrix}1&0&0\\0&1&0\\1&1&1\\0&1&3\end{pmatrix}}}
A
B
−
1
b
=
(
200
300
400
600
)
{\displaystyle A_{B}^{-1}b={\begin{pmatrix}200\\300\\400\\600\end{pmatrix}}}
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
x
3
{\displaystyle x_{3}}
b
z
1
6
13
0
s
1
{\displaystyle s_{1}}
1
0
0
200
s
2
{\displaystyle s_{2}}
0
1
0
300
s
3
{\displaystyle s_{3}}
1
1
1
400
s
4
{\displaystyle s_{4}}
0
1
3
600
x
1
,
x
2
,
x
3
{\displaystyle x_{1},x_{2},x_{3}}
s
1
,
s
2
,
s
3
,
s
4
{\displaystyle s_{1},s_{2},s_{3},s_{4}}
c
N
T
−
c
N
T
A
B
−
1
A
N
{\displaystyle c_{N}^{T}-c_{N}^{T}A_{B}^{-1}A_{N}}
A
B
−
1
A
N
{\displaystyle A_{B}^{-1}A_{N}}
A
B
−
1
b
{\displaystyle A_{B}^{-1}b}
−
c
B
T
A
B
−
1
b
{\displaystyle -c_{B}^{T}A_{B}^{-1}b}
Für das Update eines Tableau wird eine neue zulässige Basis bestimmt, indem ein Basisvektor durch einen Nichtbasisvektor ausgetauscht wird.
Die Menge der Nichtbasisvektoren, die getauscht werden können, ist über die positiven Koeffizienten c der Zielfunktion definiert als:
E
=
{
j
|
c
x
x
j
>
0
}
{\displaystyle E=\{j|c_{x}x_{j}>0\}}
E
=
∅
{\displaystyle E=\emptyset }
L
j
=
{
i
|
x
j
i
>
0
}
{\displaystyle L_{j}=\{i|x_{j}^{i}>0\}}
L
j
=
∅
{\displaystyle L_{j}=\emptyset }
j
∈
E
{\displaystyle j\in E}
c
T
x
{\displaystyle c^{T}x}
x
j
{\displaystyle x_{j}}
Berechne für eine zulässige Basis, das zugehörige Tableau. Nun wird E bestimmt. Wenn
E
=
∅
{\displaystyle E=\emptyset }
j
∈
E
{\displaystyle j\in E}
L
j
{\displaystyle L_{j}}
L
j
=
∅
{\displaystyle L_{j}=\emptyset }
i
∈
L
j
{\displaystyle i\in L_{j}}
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
x
3
{\displaystyle x_{3}}
b
z
1
6
13
0
s
1
{\displaystyle s_{1}}
1
0
0
200
s
2
{\displaystyle s_{2}}
0
1
0
300
s
3
{\displaystyle s_{3}}
1
1
1
400
s
4
{\displaystyle s_{4}}
0
1
3
600
E
=
{
j
|
c
x
x
j
>
0
}
=
{
1
,
2
,
3
}
{
x
1
,
x
2
,
x
3
}
{\displaystyle E=\{j|c_{x}x_{j}>0\}=\{1,2,3\}~\{x_{1},x_{2},x_{3}\}}
L
1
=
{
i
|
x
1
i
>
0
}
=
{
1
,
3
}
{
s
1
,
s
3
}
{\displaystyle L_{1}=\{i|x_{1}^{i}>0\}=\{1,3\}~\{s_{1},s_{3}\}}
L
2
=
{
i
|
x
2
i
>
0
}
=
{
2
,
3
,
4
}
{
s
2
,
s
3
,
s
4
}
{\displaystyle L_{2}=\{i|x_{2}^{i}>0\}=\{2,3,4\}~\{s_{2},s_{3},s_{4}\}}
L
3
=
{
i
|
x
3
i
>
0
}
=
{
3
,
4
}
{
s
3
,
s
4
}
{\displaystyle L_{3}=\{i|x_{3}^{i}>0\}=\{3,4\}~\{s_{3},s_{4}\}}
[ Bearbeiten ] Als erstes werden die größten Koeffizienten in der Zielfunktion gewählt (Dantzig). Eine andere Möglichkeit ist das steepest-edge pricing, welches die Kombination aus Spalten- und Zeilenvektor wählt, die den größten Zuwachs für die Zielfunktion bringt. Oder der kleinste Index wird gewählt. Die letzte Möglichkeit ist eine zufällige Auswahl.
Heuristik: Ersetze einen Basisvektor durch den Nichtbasisvektor, der den größten Zugewinn für die Zielfunktion bringt.
x
1
{\displaystyle x_{1}}
0
≤
s
1
=
200
−
x
1
{\displaystyle 0\leq s_{1}=200-x_{1}}
0
≤
s
3
=
400
−
x
1
{\displaystyle 0\leq s_{3}=400-x_{1}}
x
1
=
m
i
n
(
200
,
400
)
=
200
⇒
z
=
200
{\displaystyle x_{1}=min(200,400)=200\Rightarrow z=200}
Hier wird die Zeile von
s
1
u
n
d
s
3
{\displaystyle s_{1}~und~s_{3}}
x
1
{\displaystyle x_{1}}
x
1
{\displaystyle x_{1}}
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
0
≤
s
2
=
300
−
x
2
{\displaystyle 0\leq s_{2}=300-x_{2}}
0
≤
s
3
=
400
−
x
2
{\displaystyle 0\leq s_{3}=400-x_{2}}
0
≤
s
4
=
600
−
x
2
{\displaystyle 0\leq s_{4}=600-x_{2}}
x
2
=
m
i
n
(
300
,
400
,
600
)
=
300
⇒
z
=
1800
{\displaystyle x_{2}=min(300,400,600)=300\Rightarrow z=1800}
Hier wird die Zeile von
s
2
,
s
3
u
n
d
s
4
{\displaystyle s_{2},s_{3}~und~s_{4}}
x
2
{\displaystyle x_{2}}
x
2
{\displaystyle x_{2}}
x
2
{\displaystyle x_{2}}
x
3
{\displaystyle x_{3}}
0
≤
s
3
=
400
−
x
3
{\displaystyle 0\leq s_{3}=400-x_{3}}
0
≤
s
4
=
600
−
3
x
3
{\displaystyle 0\leq s_{4}=600-3x_{3}}
x
3
=
m
i
n
(
400
,
200
)
=
200
⇒
z
=
2600
{\displaystyle x_{3}=min(400,200)=200\Rightarrow z=2600}
Hier wird die Zeile von
s
3
u
n
d
s
4
{\displaystyle s_{3}~und~s_{4}}
x
3
{\displaystyle x_{3}}
x
3
{\displaystyle x_{3}}
x
3
{\displaystyle x_{3}}
s
4
{\displaystyle s_{4}}
x
3
{\displaystyle x_{3}}
Der neue Wert von
x
3
{\displaystyle x_{3}}
s
4
=
600
−
x
2
−
3
x
3
⇔
x
3
=
200
−
x
2
3
−
s
4
3
{\displaystyle s_{4}=600-x_{2}-3x_{3}\Leftrightarrow x_{3}=200-{\frac {x_{2}}{3}}-{\frac {s_{4}}{3}}}
Dieser Wert wird nun eingesetzt.
z
=
x
1
+
6
x
2
+
13
⋅
(
200
−
x
2
3
−
s
4
3
)
=
x
1
+
5
3
x
2
−
13
3
s
4
+
2600
{\displaystyle z=x_{1}+6_{x_{2}}+13\cdot (200-{\frac {x_{2}}{3}}-{\frac {s_{4}}{3}})=x_{1}+{\frac {5}{3}}x_{2}-{\frac {13}{3}}s_{4}+2600}
s
3
=
400
−
x
1
−
x
2
−
(
200
−
x
2
3
−
s
4
3
)
=
200
−
x
1
−
2
3
x
2
+
s
4
3
{\displaystyle s_{3}=400-x_{1}-x_{2}-(200-{\frac {x_{2}}{3}}-{\frac {s_{4}}{3}})=200-x_{1}-{\frac {2}{3}}x_{2}+{\frac {s_{4}}{3}}}
x
3
=
200
−
x
2
3
−
s
4
3
{\displaystyle x_{3}=200-{\frac {x_{2}}{3}}-{\frac {s_{4}}{3}}}
Das neue Tableau sieht nun so aus:
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
s
4
{\displaystyle s_{4}}
b
z
1
5
3
{\displaystyle {\frac {5}{3}}}
−
13
3
{\displaystyle -{\frac {13}{3}}}
-2600
s
1
{\displaystyle s_{1}}
1
0
0
200
s
2
{\displaystyle s_{2}}
0
1
0
300
s
3
{\displaystyle s_{3}}
1
2
3
{\displaystyle {\frac {2}{3}}}
−
1
3
{\displaystyle -{\frac {1}{3}}}
200
x
3
{\displaystyle x_{3}}
0
1
3
{\displaystyle {\frac {1}{3}}}
1
3
{\displaystyle {\frac {1}{3}}}
200
Was haben wir nun gemacht?
Von der Basis
B
=
(
s
1
,
s
2
,
s
3
,
s
4
)
{\displaystyle B=(s_{1},s_{2},s_{3},s_{4})}
B
′
=
(
s
1
,
s
2
,
s
3
,
x
3
)
{\displaystyle B'=(s_{1},s_{2},s_{3},x_{3})}
T
B
′
=
(
c
N
′
T
−
c
B
′
T
A
B
′
−
1
A
N
′
−
c
B
′
T
A
B
′
−
1
b
A
B
′
−
1
A
N
′
A
B
′
−
1
b
)
{\displaystyle T_{B}'={\begin{pmatrix}c_{N'}^{T}-c_{B'}^{T}A_{B'}^{-1}A_{N'}&-c_{B'}^{T}A_{B'}^{-1}b\\A_{B'}^{-1}A_{N'}&A_{B'}^{-1}b\end{pmatrix}}}
A
B
′
=
(
1
0
0
0
0
1
0
0
0
0
1
1
0
0
0
3
)
{\displaystyle A_{B'}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&1\\0&0&0&3\end{pmatrix}}}
A
B
′
−
1
=
(
1
0
0
0
0
1
0
0
0
0
1
−
1
3
0
0
0
1
3
)
{\displaystyle A_{B'}^{-1}={\begin{pmatrix}1&0&0&0\\0&1&0&0\\0&0&1&-{\frac {1}{3}}\\0&0&0&{\frac {1}{3}}\end{pmatrix}}}
A
N
=
(
1
0
0
0
1
0
1
1
0
0
1
1
)
{\displaystyle {A_{N}}={\begin{pmatrix}1&0&0\\0&1&0\\1&1&0\\0&1&1\end{pmatrix}}}
A
B
′
−
1
A
N
=
(
1
0
0
0
1
0
1
2
3
−
1
3
0
1
3
1
3
)
{\displaystyle A_{B'}^{-1}A_{N}={\begin{pmatrix}1&0&0\\0&1&0\\1&{\frac {2}{3}}&-{\frac {1}{3}}\\0&{\frac {1}{3}}&{\frac {1}{3}}\end{pmatrix}}}
A
B
′
−
1
b
=
(
200
300
200
200
)
{\displaystyle {A_{B'}^{-1}b}={\begin{pmatrix}200\\300\\200\\200\end{pmatrix}}}
c
T
=
(
1
6
0
0
0
0
13
)
=
(
c
N
′
T
c
B
′
T
)
{\displaystyle c^{T}={\begin{pmatrix}1&6&0&0&0&0&13\end{pmatrix}}={\begin{pmatrix}c_{N'}^{T}&c_{B'}^{T}\end{pmatrix}}}
c
N
′
T
−
c
B
′
T
A
B
′
−
1
A
N
′
=
(
1
5
3
−
13
3
)
{\displaystyle c_{N'}^{T}-c_{B'}^{T}A_{B'}^{-1}A_{N'}={\begin{pmatrix}1&{\frac {5}{3}}&-{\frac {13}{3}}\end{pmatrix}}}
−
c
B
T
A
B
−
1
b
=
−
2600
{\displaystyle -c_{B}^{T}A_{B}^{-1}b=-2600}
E
=
{
j
|
c
x
x
j
>
0
}
=
{
1
,
2
}
{
x
1
,
x
2
}
{\displaystyle E=\{j|c_{x}x_{j}>0\}=\{1,2\}~\{x_{1},x_{2}\}}
L
1
=
{
i
|
x
1
i
>
0
}
=
{
1
,
3
}
{
s
1
,
s
3
}
{\displaystyle L_{1}=\{i|x_{1}^{i}>0\}=\{1,3\}~\{s_{1},s_{3}\}}
L
2
=
{
i
|
x
2
i
>
0
}
=
{
2
,
3
,
4
}
{
s
2
,
s
3
,
x
3
}
{\displaystyle L_{2}=\{i|x_{2}^{i}>0\}=\{2,3,4\}~\{s_{2},s_{3},x_{3}\}}
Heuristik: Ersetze einen Basisvektor durch den Nichtbasisvektor, der den größten Zugewinn für die Zielfunktion bringt.
x
1
{\displaystyle x_{1}}
0
≤
s
1
=
200
−
x
1
{\displaystyle 0\leq s_{1}=200-x_{1}}
0
≤
s
3
=
200
−
x
1
{\displaystyle 0\leq s_{3}=200-x_{1}}
x
1
=
200
⇒
z
=
2800
{\displaystyle x_{1}=200\Rightarrow z=2800}
Hier wird die Zeile von
s
1
u
n
d
s
3
{\displaystyle s_{1}~und~s_{3}}
x
1
{\displaystyle x_{1}}
x
1
{\displaystyle x_{1}}
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
0
≤
s
2
=
300
−
x
2
{\displaystyle 0\leq s_{2}=300-x_{2}}
0
≤
s
2
=
200
−
2
3
x
2
{\displaystyle 0\leq s_{2}=200-{\frac {2}{3}}x_{2}}
0
≤
x
2
=
200
−
1
3
x
2
{\displaystyle 0\leq x_{2}=200-{\frac {1}{3}}x_{2}}
x
2
=
m
i
n
(
300
,
600
)
=
300
⇒
z
=
4400
{\displaystyle x_{2}=min(300,600)=300\Rightarrow z=4400}
Hier wird die Zeile von
s
2
,
s
3
u
n
d
x
3
{\displaystyle s_{2},s_{3}~und~x_{3}}
x
2
{\displaystyle x_{2}}
x
2
{\displaystyle x_{2}}
x
2
{\displaystyle x_{2}}
s
2
{\displaystyle s_{2}}
x
2
{\displaystyle x_{2}}
Der neue Wert von
x
2
{\displaystyle x_{2}}
s
2
=
300
−
x
2
⇔
x
2
=
300
−
s
2
{\displaystyle s_{2}=300-x_{2}\Leftrightarrow x_{2}=300-s_{2}}
z
=
x
1
+
5
3
⋅
(
300
−
s
2
)
−
13
3
s
4
+
2600
=
x
1
−
5
3
s
2
−
13
3
s
4
+
3100
{\displaystyle z=x_{1}+{\frac {5}{3}}\cdot (300-s_{2})-{\frac {13}{3}}s_{4}+2600=x_{1}-{\frac {5}{3}}s_{2}-{\frac {13}{3}}s_{4}+3100}
s
3
=
200
−
x
1
+
2
3
⋅
(
300
−
s
2
)
+
s
4
3
=
−
x
1
+
2
3
s
2
+
s
4
3
{\displaystyle s_{3}=200-x_{1}+{\frac {2}{3}}\cdot (300-s_{2})+{\frac {s_{4}}{3}}=-x_{1}+{\frac {2}{3}}s_{2}+{\frac {s_{4}}{3}}}
x
3
=
200
−
1
3
⋅
(
300
−
s
2
)
−
s
4
3
=
100
+
1
3
s
2
−
s
4
3
{\displaystyle x_{3}=200-{\frac {1}{3}}\cdot (300-s_{2})-{\frac {s_{4}}{3}}=100+{\frac {1}{3}}s_{2}-{\frac {s_{4}}{3}}}
Das neue Tableau sieht nun so aus:
x
1
{\displaystyle x_{1}}
s
2
{\displaystyle s_{2}}
s
4
{\displaystyle s_{4}}
b
z
1
−
5
3
{\displaystyle -{\frac {5}{3}}}
−
13
3
{\displaystyle -{\frac {13}{3}}}
-3100
s
1
{\displaystyle s_{1}}
1
0
0
200
x
2
{\displaystyle x_{2}}
0
1
0
300
s
3
{\displaystyle s_{3}}
1
−
2
3
{\displaystyle -{\frac {2}{3}}}
−
1
3
{\displaystyle -{\frac {1}{3}}}
0
x
3
{\displaystyle x_{3}}
0
−
1
3
{\displaystyle -{\frac {1}{3}}}
1
3
{\displaystyle {\frac {1}{3}}}
100
E
=
{
j
|
c
x
x
j
>
0
}
=
{
1
}
{
x
1
}
{\displaystyle E=\{j|c_{x}x_{j}>0\}=\{1\}~\{x_{1}\}}
L
1
=
{
i
|
x
1
i
>
0
}
=
{
1
,
3
}
{
s
1
,
s
3
}
{\displaystyle L_{1}=\{i|x_{1}^{i}>0\}=\{1,3\}~\{s_{1},s_{3}\}}
Ersetze einen Basisvektor durch den Nichtbasisvektor, der den größten Zugewinn für die Zielfunktion bringt. Es müssen nur Terme aus z mit positivem Vorzeichen betrachtet werden, d.h. es bleibt nur noch
x
1
{\displaystyle x_{1}}
x
1
{\displaystyle x_{1}}
0
≤
s
1
=
200
−
x
1
{\displaystyle 0\leq s_{1}=200-x_{1}}
0
≤
s
3
=
0
−
x
1
{\displaystyle 0\leq s_{3}=0-x_{1}}
x
1
=
m
i
n
(
200
,
0
)
⇒
z
=
3100
{\displaystyle x_{1}=min(200,0)\Rightarrow z=3100}
Nun wird
s
3
{\displaystyle s_{3}}
x
1
{\displaystyle x_{1}}
s
3
=
−
x
1
+
2
3
s
2
+
s
4
3
⇔
x
1
=
−
s
3
+
2
3
s
2
+
s
4
3
{\displaystyle s_{3}=-x_{1}+{\frac {2}{3}}s_{2}+{\frac {s_{4}}{3}}\Leftrightarrow x_{1}=-s_{3}+{\frac {2}{3}}s_{2}+{\frac {s_{4}}{3}}}
z
=
−
s
3
+
2
3
s
2
+
s
4
3
−
5
3
s
2
−
13
3
s
4
+
3100
=
−
s
3
−
s
2
−
4
s
4
+
3100
{\displaystyle z=-s_{3}+{\frac {2}{3}}s_{2}+{\frac {s_{4}}{3}}-{\frac {5}{3}}s_{2}-{\frac {13}{3}}s_{4}+3100=-s_{3}-s_{2}-4s_{4}+3100}
s
1
=
200
−
(
−
s
3
−
2
3
s
2
−
s
4
3
)
=
200
+
s
3
+
2
3
s
2
+
s
4
3
{\displaystyle s_{1}=200-(-s_{3}-{\frac {2}{3}}s_{2}-{\frac {s_{4}}{3}})=200+s_{3}+{\frac {2}{3}}s_{2}+{\frac {s_{4}}{3}}}
Das neue Tableau sieht nun so aus:
s
3
{\displaystyle s_{3}}
s
2
{\displaystyle s_{2}}
s
4
{\displaystyle s_{4}}
b
z
-1
-1
-4
-3100
s
1
{\displaystyle s_{1}}
-1
2
3
{\displaystyle {\frac {2}{3}}}
1
3
{\displaystyle {\frac {1}{3}}}
200
x
2
{\displaystyle x_{2}}
0
1
0
300
x
1
{\displaystyle x_{1}}
1
−
2
3
{\displaystyle -{\frac {2}{3}}}
1
3
{\displaystyle {\frac {1}{3}}}
0
x
3
{\displaystyle x_{3}}
0
−
1
3
{\displaystyle -{\frac {1}{3}}}
1
3
{\displaystyle {\frac {1}{3}}}
100
Die Zielfunktion kann nun nicht weiter verbessert werden. Unser x ist nun (0,300,100) und unser z ist 3100.
Das Simplex-Verfahren löst ein lineares Programm in endlich vielen Schritten oder stellt seine Unlösbarkeit oder Unbeschränktheit fest. Im Worstcare hat es eine exponentielle Laufzeit, unabhängig von den gewählten Pivotregeln. In der Praxis ist es sehr effizient.