Kurs:Astronomie im Freien

Projekt
Projekttitel	Astronomie im Freien
Ansprechpartner	Klaus-Dieter Keller
Laufzeit	1 bis 3 Doppelstunden
Kurzbeschreibung
Astronomie-Praktikum am Margarete-Steiff-Gymnasium Giengen für die Kursstufe 1

Ablauf

Das Praktikum findet auf dem Schießberg statt. Gestartet wird am Pavillon, danach geht es über die Lindenallee zum Tanzkreis und zum Aussichtsturm. Nach zwei gemeinsamen Aufgaben zu Beginn (Planetenweg und Milchstraße) durchlaufen die Zweierteams die weiteren Aufgaben in beliebiger Reihenfolge selbständig. Die Entfernungen werden mit großen Schritten gemessen, die dann 1 Meter groß sind.

Hier geht es zu den Lösungen zu den meisten Aufgaben.

Material

Bitte auf passende Kleidung und festes Schuhwerk achten, man läuft nur zu Beginn auf Asphalt.

Jedes Zweiterteam benötigt

Schreibblock und Stift
Taschenrechner, trigonometrische Funktionen im DEG-Modus müssen möglich sein (evtl. Smartphone)
Meterstab
Geodreieck zur Winkelmessung
Wasserwaage (evtl. Smartphone-App)

Daten

Die Daten stammen von der Liste der Planeten des Sonnensystems und sind auf vier geltende Ziffern gerundet.

Objekt	Radius in km	Große Bahnhalbachse in km	Bemerkung
Sonne	696.300	-
Merkur	2.440	57.910.000
Venus	6.052	108.200.000
Erde	6.378	149.600.000
Mars	3.397	227.900.000
Jupiter	71.490	778.400.000
Saturn	60.270	1.427.000.000
Uranus	25.560	2.871.000.000
Neptun	24.760	4.498.000.000

Mond	1.737	384.400	Entfernung zur Erde

Aufgabe: Planetenweg

Wenn die Sonne auf einen Durchmesser von 10 cm geschrumpft wird, erhält man eine Abbildung im Maßstab 1:14.000.000.000 (1:14 Milliarden). Die Modell-Sonne steht im Pavillion auf dem Schießberg. Alle acht Planeten und der Mond werden den Teilnehmern oder Gruppen zugeteilt. Berechne mit dem Maßstab und mit den Daten oben

den Durchmesser deines Modells (Tipp: Berechne zuerst den Modellradius)
den Abstand deines Modellobjekts von der Modell-Sonne.

Suche ein Steinchen mit diesem Durchmesser und positioniere dich auf der Lindenallee im Modellabstand von der Sonne; pro Meter einen großen Schritt. Das Besondere: Wir haben jetzt ein Modell, bei dem der Maßstab für Durchmesser und Abstände der gleiche ist. Viele Planetenwege haben den Maßstab nur im Abstand; viele Abbildungen der Planeten haben den Maßstab nur im Durchmesser.

Maßstäbliche Abstände bei einem Planetenweg
Maßstäbliche Durchmesser bei einer Abbildung

Aufgabe: Milchstraße

Unsere Galaxie, die Milchstraße, besitzt einen Durchmesser von 200.000 Lichtjahren und eine Dicke von 1.000 Lichtjahren. In der Mitte ist sie dicker, nämlich 15.000 Lichtjahre.

Die nächste Galaxie ist die Andromedagalaxie. Sie besitzt den gleichen Durchmesser wie die Milchstraße und ist von ihr 2.500.000 Lichtjahre entfernt.

a) Miss den Durchmesser des Tanzkreises in Metern.

b) Wenn die Milchstraße so groß ist wie der Tanzkreis, wie dick wäre sie dann außen und in der Mitte?

c) In welcher Entfernung befindet sich dann die Andromedagalaxie?

Aufgabe: Bogenminute und Bogensekunde

Person in 100m Abstand

Die zwei Personen eines Teams stehen 100 m auseinander.

a) Berechne zuerst die Höhe/Breite h von Objekten, die in der Entfernung 100 m jeweils 1 Grad, 1 Bogenminute und 1 Bogensekunde groß scheinen.

$h=100m\cdot tan(\alpha )$

b) Jeder sucht Objekte der jeweiligen Größe. Zeigt sie euch gegenseitig in 100 m Entfernung.

Aufgabe: Sonnenfinsternis

Je nach Position auf den elliptischen Bahnen erscheinen Mond und Sonne leicht unterschiedlich groß:

Mond: 0,49° bis 0,56°
Sonne: 0,52° bis 0,54°

Aber grob gesagt erscheinen sie uns gleich groß und sie passen fast exakt „aufeinander“.

a) Berechne aus dem Verhältnis der beiden Radien von Sonne und Mond den Faktor, um den die Sonne größer ist als der Mond.

b) Suche zwei Objekte, die sich um diesen Faktor unterscheiden, das Größere könnte eine Baumkrone oder der Tanzkreis sein. Ordne die Objekte so an, dass genau eine „Finsternis“ enststeht.

c) Miss die Abstände von deinem Auge zu den beiden Objekten und berechne das Verhältnis. Vergleiche zur Kontrolle mit dem Verhältnis der Abstände von Erde zu Mond und Erde zur Sonne aus a).

Aufgabe: Höhe des Aussichtsturms

Bestimme mit einer der drei folgenden Methoden die Höhe des Aussichtsturms. Die Formel in der letzten Zeile zeigt dir jeweils, was du messen musst.

Bestimmung der Turmhöhe mit einem gleichseitigen Dreieck (45°-Methode)
a ist deine Augenhöhe. Benutze die 45°-Ecke des Geodreiecks, um die Spitze des Turms anzupeilen. Wenn du die Spitze siehst, bist du (fast) so weit weg wie der Turm hoch ist.
$b=d$
$h=a+b=a+d$
Bestimmung der Turmhöhe mit dem Strahlensatz
s ist die Länge eines Stabs, c ist ungefähr die Armlänge
${\frac {h}{s}}={\frac {d}{c}}$
$h={\frac {s\cdot d}{c}}$
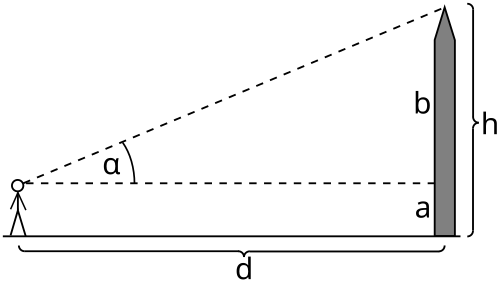
Bestimmung der Turmhöhe mit Trigonometrie
a ist deine Augenhöhe, $\alpha$ wird mit dem Geodreieck bestimmt
$b=d\cdot \tan \alpha$
$h=a+b=a+d\cdot \tan \alpha$

geplante Aufgaben

Parallaxenmethode

Wo ist Norden?

Wie groß ist die Erde?