Kurs:Java – ein schneller Einstieg/Klassen und Objekte
- Einleitung
- Grundlagen
- Rechnen
- GUI
- Events
- Frames
- Usability
- Exceptions
- Javadoc
- Anhang
Klassen und Objekte
[Bearbeiten]Die objektorientierte Programmierung erzeugt sogenannte Objekte aus Klassen. Dieser Vorgang wird Instanziierung genannt, was dem Anfänger keinesfalls weiterhilft. Auch Erklärungen über Reservierung von Speicherplatz durch Anlegen von Kopien der entsprechenden Klassen helfen wenig. Hier hilft nur reine Anschauung. Allerdings handelt es sich bei Objekt entweder um einen sehr abstrakten oder um einen sehr realen Begriff - je nach Vorstellung.
Dieser Kurs beginnt mit der Annahme, dass die abstrakte Betrachtungsweise gewählt wurde. Andere Vorstellungen werden natürlich ebenfalls berücksichtigt, aber eben erst nach der Instanziierung.
Objektsammlungen
[Bearbeiten]Um hier etwas Licht in die Sache zu bringen, wird der Instanziierungsvorgang umgekehrt; aus Objekten sollen erst einmal die Klassen hergeleitet werden.
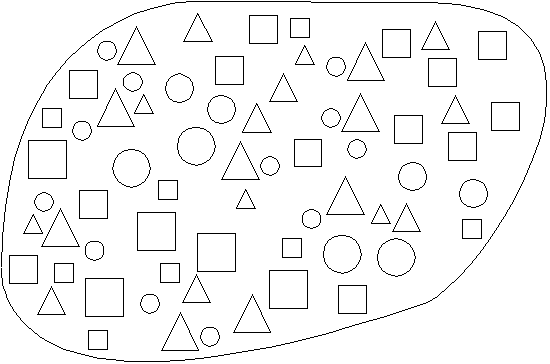
Hier ist offensichtlich eine Ansammlung von Objekten geometrischer Art vorhanden. Eine Klassifizierung bedarf zunächst einmal einer Ordnung. Jedoch ist Ordnung ein relativer Begriff. Soll nun nach Größe geordnet werden oder ist es angebrachter, nach Formen zu unterscheiden? Soll die Hierarchie von links nach rechts oder von oben nach unten gerichtet sein?
Am einfachsten ist es in diesem Fall, alle genannten Überlegungen gleichzeitig anzuwenden. Dabei muss aber peinlich genau darauf geachtet werden, die Grenzen nicht zu verletzen. Diese Grenzen sind hier durch die konvexe Hülle gegeben. Auch darf bei der Einführung einer Ordnungsrelation kein Element (Objekt) fehlen oder hinzugefügt werden.
Die jetzt eingeführte Ordnung der Objekte folgt in vertikaler Richtung den Formen und in horizontaler den Größen. Die vorhandenen Abgrenzungen seien durchgehende Linien. Die Objekte wurden innerhalb der umhüllenden Grenze in kleinere Ansammlungen zusammengefasst oder gekapselt. Es ergeben sich neun Teile.
Alle Objekte zwischen zwei durchgehenden Grenzlinien bilden wiederum abgeschlossene Teile der Ansammlung (die horizontalen Linien seien ebenfalls durchgehend, auch wenn diese Vorstellung etwas Abstraktionsvermögen voraussetzt) mit jeweils drei Teilen. So lassen sich die Objekte entweder in einer umhüllenden, formgebenden Ordnung oder in einer umhüllenden größenbegrenzenden Ordnung zusammenfassen.
Objektmenge
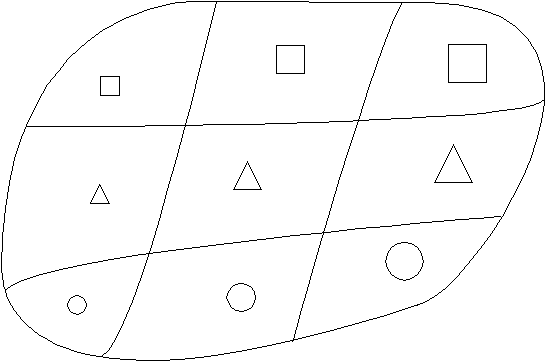
[Bearbeiten]Bis jetzt ist es gelungen, gleichartige Objekt in abgeschlossenen Bereichen unterzubringen. Jeder dieser Bereiche ist ein Element der Menge eben dieser Bereiche. Es liegt deshalb eine Menge vor, weil die einzelnen Elemente wohlunterscheidbar sind. Diese Unterteilung hat natürlich einen eigenen Begriff und wird als Faserung einer Menge bezeichnet. In jedem Fall ist jetzt alles Formbasierende in horizontalen Fasern, alles Größenbasierende in vertikalen Fasern untergebracht. So verläuft die Faser der großen Objekte ganz rechts von oben nach unten, die Faser der runden Objekte dagegen ganz unten von links nach rechts.
Die Elemente innerhalb einer Faser werden Zellen genannt. Jetzt besteht das nächste Problem darin, die Objekte innerhalb der Zellen so umzugestalten, dass jede Zelle als Teilmenge der gesamten Objektmenge vorhanden ist. Hier kommt ein wesentlicher Gesichtspunkt der Mengentheorie ins Spiel - die Wohlunterscheidbarkeit. Eine Menge besteht nur aus unterscheidbaren Objekten. Es existiert keine Menge der Form M = {4,4}, denn die Elemente sind voneinander nicht zu unterscheiden. Jede Zelle hat aber mehr als ein Element in sich, was tun?
Nun sind Zahlen nichts anderes als Faktoren und damit prinzipell nichtssagend. Mit 15 kann niemand etwas anfangen; fünfzehn Was? Burger, Euros, Cents, Millimeter oder was? Von diesen nichtssagenden Gebilden sollte Abstand genommen werden. Die Elemente innerhalb der Fasern sollen nun in (Teil)mengen umgewandelt werden und enthalten damit nur noch ein einziges Objekt.
Eine erste Klassifizierung
[Bearbeiten]Jetzt repräsentiert jede Zelle die Klasse des Elements das sie enthält und kann beliebig viele Objekte dieser Elemente bereitstellen. Aber noch mehr wurde erreicht; jede Faser ist nun eine übergeordnete Klasse der jeweiligen Fasern. So ist die linke Faser die Menge aller Klassen kleiner Objekte und die unterste Faser die Klasse aller runden Objekte
Die jetzt vorhandene Menge ist einem Einkaufskatalog mit jeweils einem Abbild eines Produkts vergleichbar. Von jedem Element einer Zelle kann eine gewisse Anzahl bestellt werden. Jeder Zelle wird so die faktorisiernde Anzahl einfach als Eigenschaft zugeordnet.
Zelle der kleinen Dreiecke: Anzahl 5; oder Zelle der großen Kreise: Anzahl 4.
Menge der Klassen geometrischer Objekte
[Bearbeiten]Der letzte Schritt zur Klassifizierung besteht in der Konfektionierung. In Kaufhäusern werden oft T-Shirts in den Größen S, M und L angeboten. Diese amerikanischen Konfektionsgrößen (Small, Medium, Large) liegen auch hier vor. Jede horizontale Faser besitzt die gleiche Unterteilung seiner Zellen. Wer Analogien zur Schnäppchenjagd im Kaufhaus mag, kann die unterschiedlichen Formen durch T-, Polo- und Sweat-Shirts ersetzen. In jedem Fall kann die horizontale Unterteilung durch Einführung der Konfektionsgröße entfallen.
Jetzt ist die Klassifizierung der anfangs vorhandenen Objekte abgeschlossen. Für Freunde des realen Bezugs kann die hier dargestellt Klassenmenge als Hersteller von Shirts angesehen werden. Es existieren drei Klassen, die jeweils eine Hemdensorte erzeugen können. Damit die Erzeugung funktioniert, muss in diesem Fall die Anzahl und Größe der gewünschten Objekte angegeben werden.
Zahlen und Werte
[Bearbeiten]Eine Zahl repräsentiert gemeinhin einen Wert. Es existieren die unterschiedlichsten Möglichkeiten Zahlen in Werte umzuwandeln. So war die Zeichenfolge "IV" vor geraumer Zeit eine durchaus übliche Repräsentation des Wertes "vier". Bis heute hat sich nichts an den Unterscheidungszwang zwischen Zeichenfolge/Zahl/Wert geändert. So ist denn auch in Java dieses Problem vorhanden.
Wenn irgendwo im Quelltext die Zeichenfolge 123 auftaucht, vermutet der Compiler immer den Wert einer ganzen Zahl dahinter. Wenn jedoch "123" gefunden wird, steht für den Compiler fest, dass es sich um einen Text handelt. Nun ist es sinnvoll, den verwendeten Dingen einen Namen zu geben und diesen Namen statt Zeichenfolge/Wert/Text zu verwenden. Diese Namen werden unter dem Begriff Variablen zusammengefasst und spielen in der Programmierung die zentrale Rolle. Variablen informieren den Compiler über den Ort des Wertes (sie referenzieren einen Speicherbereich) und über den Aufbau des Wertes. Mag die Notwendigkeit einer Ortsangabe noch einzusehen sein, so treten doch bei "Art des Wertes" erste Verständnisprobleme auf.
Zunächst sollen die Begriffe "Zeichenfolge", "Zahl" und "Wert" getrennt werden. Diese Unterscheidung bereitet am Anfang die größten Probleme.
- Zeichenfolge
- Eingaben des Anwenders sind Zeichenfolgen. Unabhängig davon, ob nun ausschließlich Ziffern oder Buchstaben eingetippt werden, es handelt sich immer nur um eine Aneinanderreihung von Zeichen.
- Zahl
- Der Anwender gibt eine Folge von Ziffern ein, also eine Zeichenfolge. Das Programm (nicht der Compiler) muss diese Folge in eine Zahl umwandeln. Wie diese Aufgabe bewältigt wird, zeigt ein anschließender Abschnitt. Hier genügt es, die Notwendigkeit der Umwandlung zu erkennen. Der Compiler wandelt diese Zahl nun in einen Wert.
- Wert
- Mit Werten wird ein Anwender nicht konfrontiert. Werte sind systeminterne Bitfolgen, die nach bestimmten Regeln aufgebaut sind (IEEE 754 ist eine solche Regel). Auch Programmierer sind kaum mit diesen Interna konfrontiert, es sei denn, es sollen schnelle Programme geschrieben werden. Zu diesem Zeitpunkt ist nur wichtig, dass der Computer nur mit Werten umgehen kann, während der Anwender und auch der Programmierer nur an den Ergebnissen interessiert ist. Ergebnisse müssen aufbereitet werden, damit sie verständlich sind. Für die erste Überprüfung werden sie meist wieder in eine Zeichenfolge umgewandelt, damit diese angezeigt werden können.
Der Umgang mit Zahlen auf einem Computer ist also eine Art Keislauf. Zunächst wird eine "Zeichenfolge" entgegengenommen und in eine Zahl umgewandelt. Der Compiler macht einen Wert daraus und eine Berechnung (z.B. diese Zahl +5) kann angewiesen werden. Der Wert wird nun dieser Berechnung unterzogen und liegt im systeminternen Format vor. Zur Überprüfung muss nun der Wert in eine Zahl und weiter in eine Zeichenfolge gewandelt werden. Letztere wird dann angezeigt.
Detaillierte Beschreibung einer Addition
[Bearbeiten]Das Thema "Zahlen" ist derart wichtig, dass ein behutsames Herantasten an die Abläufe in Programmen sehr wichtig ist. Deshalb soll hier die Addition mit dem jetzt vorhandenen Wissen detailliert besprochen werden.
Eine Zeichenfolge der Form "26" wird unter dem Namen "Zahl1" geführt. Natürlich ist es keine Zahl, sondern ein Text (String). Eine weitere Zeichfolge "74" wird unter dem Namen "Zahl2" geführt. Wenn es sich um Zahlen handelte müsste die Addition die Zahl 100 ergeben. Im Quelltext könnte nun etwas wie
Zahl1 = 26 Zahl2 = 74 Zahl1 + Zahl2
stehen. Selbst wenn es sich um ausführbare Anweisungen handeln würde, wäre es sinnlos. Zwar stünde irgenwo im Speicher der Wert 100, aber er ist nicht erreichbar. Ihm fehlt eine Referenz. Sinnvoller, aber noch nicht ausführbar, ist folgende Schreibweise:
Zahl1 = 26 Zahl2 = 74 Ergebnis = Zahl1 + Zahl2
Das Programm kann nun über die Referenz "Ergebnis" auf den errechneten Wert zugreifen. Aus dem bisher Erarbeiteten kann eine erste Konsequenz gezogen werden.
|
Alle Werte müssen über eine Referenz verfügen. |
Ziel dieser detaillierten Auseinandersetzung mit Zahlen und Werten ist eine in Java ausführbare Programmsequenz. Java verlangt genaue Informationen über die Art der zu verarbeitenden Werte. Was ist also unter dem Begriff "Art des Wertes" zu verstehen? Ganz einfach, es ist der Typ gemeint. Tatsächlich kommt die zweite Bezeichnung der Sache bereits etwas näher.
Typen
[Bearbeiten]Oft werden Geschäftsleute in zwei Kategorien unterteilt: Die Integeren, die lieber das Geschäft ablehnen, als unseriös zu wirken und die Realisten, die sich auch mal zu ihren eigenen Gunsten "verrechnen". Diese zwei Typen können mit viel Phantasie auf Werte übertragen werden. Die Integer-Werte und die Real-Werte verhalten sich recht unterschiedlich wenn es ins Detail geht, sonst aber durchaus gleich. Integer-Werte können bedingt geteilt werden. Der Integer-Wert "fünf" teilt sich in zwei gleiche Hälften der jeweiligen Werte "zwei". Der Real-Typ würde jeweils "2,5"-wertige Hälften zulassen. Allerdings kann es vorkommen, dass eine Hälfte "2,500000001" wert ist und die andere "2,4999999997". Trotzdem würde der Real-Typ die Addition dieser beiden unterschiedlichen Werte wieder zur "5" vereinen. Richtig unangenehm wird es allerdings bei Werten um 1. Ein Integer-Wert ergibt bei eine Teilung durch 2 den Wert 0. Ein Real-Wert den 0.5 (mit der bereits erwähnten Möglichkeit zur Ungenauigkeit). Eine Überprüfung durch Addition beider Hälften wird bei Integer-Typen das fehlerhafte Ergebnis 0 und bei Real-Typen das korrekte Ergebnis 1 liefern. Offensichtlich können diese beiden Grundtypen unterteilt werden in die Merksätze:
|
Um die Nomenklatur von Java bezüglich der Reals, sie werden als Floats typisiert, etwas zu verdeutlichen, kann vielleicht folgende Vorstellung herangezogen werden:
Ein Getränk in einer Bar ist teuer, genau abgemessen aber es kann nicht gänzlich genossen werden. Ein paar Tropfen bleiben im Glas und entziehen sich dem Genuss. Beim nächsten Drink sollte das alte Glas benutzt werden, denn es wird um eben diese Tropfen voller sein. Der unweigerlich entstehende Fehler durch die Ungenauigkeit wurde halbiert.
Java hat also die Wertetypen Integer und Float. Damit aber noch nicht genug, denn es gibt auch hier noch Abstufungen. Je nach Bedarf können lange oder kurze Zahlen bearbeitet werden, je nach erforderlicher Genauigkeit. Eine komplette Liste aller Wertetypen ist im Abschnitt Variablen enthalten.
Rechnen mit typisierten Werten
[Bearbeiten]Zurück zum Aufbau einer lauffähigen Programmsequenz zur Addition zweier Zahlen. Die Werte verfügen bereits über Referenzen (Zahl1, Zahl2 und Ergebnis), es fehlten ihnen aber die Typen. Offensichtlich genügen Integer-Typen für alle Werte, denn es existieren keine Kommastellen und es soll auch nicht dividiert werden. Nun ist Java eine objektorientierte Programmiersprache und die Vermutung drängt sich auf, dass hinter all den Referenzen, Typen und Werten das eine oder andere Objekt versteckt ist. Nein, weit und breit kein Objekt. Noch nicht! Bei dem nun um die Typenangabe erweiterten Quellcode
int Zahl1 = 26; int Zahl2 = 74; int Ergebnis = Zahl1 + Zahl2;
handelt es sich um eine ausführbare Sequenz. Allerdings muss diese erst übersetzt werden, damit der Computer sie versteht. Dieser Übersetzungsvorgang soll nun prinzipiell erörtert werden (die tatsächlichen Abläufe eines Compilers werden hier natürlich nicht besprochen).
Zunächst findet der Compiler die eine Typenbezeichnung und reserviert den benötigten Speicherplatz. Jetzt wird der Bezeichner (Name) "Zahl1" gefunden und mit dem Ort des reservierten Speicherplatzes in Verbindung gebracht. Der Wert wird über den Bezeichner referenziert. Das Gleichheitszeichen "=" wird erkannt, womit der Compiler angewiesen wird, alle bis zum Semikolon ";" folgenden Zeichen irgendwie als Zahl zu interpretieren und deren Wert dann an der referenzierten Stelle abzulegen. Dieses Vorhaben wird ihm zweifellos gelingen und er verfährt mit der nächsten Zeile wieder genauso. Nun die dritte Zeile. Zunächst findet der Compiler wieder eine Typen- und eine Referenzangabe. Hinter dem Gleichheitszeichen steht jetzt zwar wieder eine Zeichenfolge (Zahl1), aber sie lässt sich nicht in eine Zahl umwandeln. Vielleicht hat diese Zeichenfolge aber etwas mit Werten zu tun. Letztendlich entpuppt sie sich als Referenz und eine Überprüfung des Typs ergibt, dass es sich um einen brauchbaren (Integer) handelt. Das Pluszeichen wird erkannt und der Compiler wird versuchen die nächste Zeichenfolge wieder als Zahl zu interpretieren. War nichts, ist wieder eine Referenz. Typ überprüfen, Typ ok. und nun aus den Referenzen und dem Pluszeichen eine Zahl zusammenbauen. Über "Zahl1" referenzierten Wert holen und merken, über "Zahl2" referenzierten Wert holen und zum gemerkten addieren. Neuen Wert merken und unter der über "Ergebnis" referenzierten Speicherstelle ablegen.
Soweit die prinzipielle Vorgehensweise des Compilers. Offensichtlich ein sehr komplexes Programm, dessen Prinzipien aber durchaus bei der täglichen Programmierarbeit hilfreich sind. Der nächste Abschnitt zeigt warum.
<< Java – ein schneller Einstieg | Klassen und Objekte | Rechnen mit eingegebenen Zahlen >>