Kurs:Räumliche Modellbildung/Gruppe 15
Gruppenseite - (RGB)
[Bearbeiten]Diese Seite enthält die gesammelten Materialien der Gruppe 15 für die Portfolioprüfung.
Teilnehmer-innen
[Bearbeiten]- Klara Ruff
- Lena Gilcher
- Shirley Betsch
Diskrete Modellierung
[Bearbeiten]SIR-Modell mit Tabellenkalkulationsprogramm
[Bearbeiten]Allgemeine Informationen
[Bearbeiten]- Die Startpunkte der einzelnen Personen werden festgelegt und die infizierte Person gewählt (1:infected ; 0:susceptible).
- Der Raum wird durch eine 20x20 Matrix dargestellt.
- Die Infektionswahrscheinlichkeit gibt an wie hoch die Wahrscheinlichkeit ist sich zu infizieren.
| A | B | C | D | E |
|---|---|---|---|---|
| x | y | |||
| Startpunkt Person 1 | 10 | 13 | 1 | |
| Startpunkt Person 2 | 3 | 5 | 0 | |
| Startpunkt Person 3 | 16 | 14 | 0 | |
| Startpunkt Person 4 | 8 | 8 | 0 | |
| Startpunkt Person 5 | 4 | 4 | 0 | |
| x | y | |||
| obere Grenzen | 20 | 20 | ||
| untere Grenzen | 0 | 0 | ||
| Infektionswahrscheinlichkeit | 0,2 |
Modellierung der Positionsänderungen aller Personen
[Bearbeiten](Beispielhaft durch Person 1 gezeigt)
- Person 1
Status am Anfang: 1 d.h Person ist infiziert
- Abfragen:
⇒12,7536268786558=WENN(B5+D6>$Allgemeines.B$11;B5-ZUFALLSZAHL()*3;WENN(B5+D6<$Allgemeines.B$12;B5+ZUFALLSZAHL()*3;B5+D6))
⇒12,7536268786558=WENN(C5+E6>$Allgemeines.C$11;C5-ZUFALLSZAHL()*3;WENN(C5+E6<$Allgemeines.C$12;C5+ZUFALLSZAHL()*3;C5+E6))
⇒2,75362687865583=-3+6*ZUFALLSZAHL()
⇒-0,005662748437095=-3+6*ZUFALLSZAHL()
| A | B | C | D | E |
|---|---|---|---|---|
| t | x | y | Bewegung in x-Richtung | Bewegung in y-Richtung |
| 0 | 10 | 13 | ||
| 1 | 12,7536268786558 | 12,9943372515629 | 2,75362687865583 | -0,005662748437095 |
| 2 | 10,917954283641 | 13,1458929666051 | -1,83567259501487 | 0,151555715042242 |
| 3 | 9,96388314304611 | 15,9229791003147 | -0,954071140594845 | 2,77708613370958 |
| 4 | 8,51250844841113 | 15,4924898240445 | -1,45137469463499 | -0,430489276270182 |
| 5 | 8,5772288908625 | 12,7624766264637 | 0,064720442451369 | -2,73001319758088 |
| 6 | 9,82651751507785 | 10,9650534345809 | 1,24928862421536 | -1,79742319188276 |
| 7 | 10,0096249152132 | 8,07713475134837 | 0,183107400135356 | -2,88791868323254 |
| 8 | 8,27631653202698 | 5,84270743285987 | -1,73330838318623 | -2,2344273184885 |
| 9 | 6,56276433307787 | 6,5481794430535 | -1,71355219894911 | 0,705472010193631 |
| 10 | 8,42119782316474 | 8,20854039214596 | 1,85843349008687 | 1,66036094909246 |
| 11 | 10,5246069551183 | 9,14207090744135 | 2,10340913195353 | 0,933530515295396 |
| 12 | 10,5110795559202 | 6,32226607972122 | -0,013527399198093 | -2,81980482772013 |
| 13 | 11,360894269437 | 4,57738612179959 | 0,849814713516773 | -1,74487995792163 |
| 14 | 10,0398705193774 | 4,85192343043513 | -1,32102375005952 | 0,274537308635539 |
| 15 | 8,8466928781919 | 2,88416570363843 | -1,19317764118554 | -1,9677577267967 |
| 16 | 6,9901049800876 | 3,92313021302957 | -1,8565878981043 | 1,03896450939114 |
| 17 | 8,42515517916673 | 5,41030564957336 | 1,43505019907913 | 1,48717543654379 |
| 18 | 9,37947664592221 | 7,8297594578109 | 0,954321466755477 | 2,41945380823754 |
| 19 | 11,6862806755774 | 5,31887514301613 | 2,30680402965515 | -2,51088431479477 |
| 20 | 9,65646807141582 | 4,41178891153317 | -2,02981260416153 | -0,907086231482955 |
| 21 | 12,219653631761 | 1,81917331023282 | 2,56318556034522 | -2,59261560130035 |
| 22 | 12,8632807163325 | 0,897372396031146 | 0,643627084571443 | -0,921800914201678 |
| 23 | 15,1019365932361 | 3,02669574165249 | 2,23865587690362 | 2,12932334562135 |
| 24 | 16,6193900638279 | 1,47051605847286 | 1,51745347059181 | -1,55617968317963 |
| 25 | 18,4283745726683 | 1,42457177592046 | 1,80898450884043 | -0,045944282552401 |
| 26 | 17,8946345272821 | 0,433348643794853 | -0,53374004538628 | -0,991223132125607 |
| 27 | 19,5989098838579 | 2,83704598705126 | 1,70427535657581 | 2,40369734325641 |
| 28 | 17,4618244073089 | 2,3262726616941 | 0,775359395067039 | -0,510773325357157 |
| 29 | 17,0704164616034 | 2,95831577511132 | -0,391407945705569 | -2,57928304793946 |
| 30 | 15,9900539448124 | 2,96480246770511 | 2,98577992253819 | 0,006486692593787 |
| 31 | 13,8346748907432 | 2,81291540256485 | -2,15537905406927 | -0,151887065140259 |
| 32 | 14,0773663314632 | 1,20682965087788 | 0,242691440720001 | -1,60608575168697 |
| 33 | 16,0810894073221 | 0,155948328248616 | 2,00372307585898 | -1,05088132262927 |
| 34 | 14,9765520759798 | 3,01689439311031 | -1,10453733134232 | -1,13353980745856 |
| 35 | 17,165544974251 | 0,78539356806105 | 2,18899289827121 | -2,23150082504926 |
| 36 | 16,4634934554289 | 1,61384047647813 | -0,702051518822128 | 0,828446908417082 |
| 37 | 18,0956895771532 | 4,17927637997317 | 1,63219612172433 | 2,56543590349504 |
| 38 | 15,4204234319744 | 3,67473657941849 | -2,67526614517883 | -0,504539800554676 |
| 39 | 15,8035696797358 | 3,53527444487542 | 0,383146247761384 | -0,139462134543075 |
| 40 | 14,605753824254 | 5,86690951168784 | -1,1978158554818 | 2,33163506681242 |
| 41 | 16,7780180044461 | 3,5939740564565 | 2,17226418019209 | -2,27293545523133 |
| 42 | 17,9266693606991 | 4,82085964299434 | 1,14865135625298 | 1,22688558653783 |
| 43 | 17,1817459974786 | 5,47203442194138 | -0,744923363220475 | 0,651174778947044 |
| 44 | 16,1418508089 | 4,28319067932935 | -1,03989518857862 | -1,18884374261203 |
| 45 | 17,6468791301006 | 4,02641674407368 | 1,50502832120068 | -0,256773935255669 |
| 46 | 18,238266063823 | 3,29999847134887 | 0,591386933722409 | -0,726418272724814 |
| 47 | 17,8047190576252 | 5,80548039443484 | 2,43449055864976 | 2,50548192308598 |
| 48 | 15,6200844908496 | 7,68979694964426 | -2,18463456677555 | 1,88431655520942 |
| 49 | 17,7750870354746 | 9,14285093208986 | 2,15500254462495 | 1,4530539824456 |
| 50 | 15,8730508808343 | 11,9795744597499 | -1,90203615464026 | 2,83672352766005 |
| 51 | 16,6829786932846 | 11,121295420428 | 0,809927812450313 | -0,858279039321862 |
| 52 | 15,8539782617851 | 12,1156127401561 | -0,829000431499503 | 0,994317319728056 |
| 53 | 17,8378094253411 | 12,8580741463164 | 1,98383116355596 | 0,742461406160339 |
| 54 | 14,8979843085182 | 12,6586755670545 | -2,93982511682292 | -0,199398579261966 |
| 55 | 14,4284521639095 | 9,67015833789943 | -0,46953214460869 | -2,98851722915505 |
| 56 | 14,7257190422845 | 8,21727445112315 | 0,297266878375 | -1,45288388677628 |
| 57 | 14,773088360179 | 10,1558295393159 | 0,047369317894501 | 1,9385550881928 |
| 58 | 15,4422934103038 | 11,0502636166708 | 0,669205050124787 | 0,894434077354877 |
| 59 | 12,7985325329135 | 11,7405537529637 | -2,64376087739026 | 0,690290136292924 |
| 60 | 14,2365321947301 | 9,15573453954939 | 1,43799966181662 | -2,58481921341436 |
Abstandsabfrage zwischen Personen
[Bearbeiten]- Mittels der euklidischen Norm wird der Abstand zwischen den Personen berechnet.
7,71340468964258=WURZEL((Person1!B6-Person2!B6)^2+(Person1!C6-Person2!C6)^2)
⇒Zugriff auf Tabellenblätter der einzelnen Personen, um die jeweiligen x- und y-Koordinaten zum jeweiligen Zeitpunkt abzurufen, sodass die euklidische Norm berechnet werden kann.
- Beispielhafter Ausschnitt der Ergebnisse der Abstandsabfrage:
| Abstand Person 1 mit Person 2 |
|---|
| 7,71340468964258 |
| 4,26554244469595 |
| 0,8402068053489 |
| 2,93410122552207 |
| 6,02357886620046 |
| 7,80980231754275 |
| 8,51000440094819 |
| 8,3790048243642 |
| 3,38116600466229 |

Abstandscheck
[Bearbeiten]- Abstandscheck zwischen Person 1 und Person 3 wird durchgeführt. Falls der Abstand zwischen beiden kleiner 2m ist, soll 1 ausgegeben werden (Zufallsexperiment wird im Weiteren durchgeführt), sonst 0 (Zufallsexperiment wird nicht durchgeführt)
1=WENN(B4<2;1;0)
| Abstandscheck |
|---|
| 0 |
| 1 |
| 0 |
| 0 |
| 1 |
| 0 |
| 0 |
| 0 |

Infektionsvorgang mittels einem Zufallexperiment und Abfrage des Infektionsstatus
[Bearbeiten]Zufallsexperiment
[Bearbeiten]- Hier wird abgefragt ob bei dem Abstandscheck zuvor eine 1 oder eine 0 ausgeworfen wurde.
- Ein Zufallsexperiment wird durchgeführt, wenn beim Abstandscheck der Abstand kleiner 2 ist.
- Beim Zufallsexperiment wird eine Zufallszahl generiert. Eine "Infektion" wird angezeigt, wenn die Zufallszahl kleiner als die Infektionswahrscheinlichkeit ist, sonst wird "keine Infektion" ausgeworfen.
keine Infektion=WENN(UND(N12=1;ODER(V11=1;Z11=1));WENN(ZUFALLSZAHL()<$Allgemeines.$B$15;"Infektion";"Keine Infektion");"0")
| Person 1 mit Person 5 |
|---|
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| Keine Infektion |
| 0 |
| 0 |
| Keine Infektion |
| 0 |
| 0 |
| 0 |
| Infektion |
| 0 |
| 0 |
Abfrage Infektionsstatus
[Bearbeiten]Abfrage Anfangsstatus Person 5: 0=$Allgemeines.E8 Abfrage Status Person 5 nach Zeitschritten: 1=WENN(Z18=1;1;WENN(ODER(AE19="Infektion";AH19="Infektion";AJ19="Infektion";AK19="Infektion");1;0)) Wenn eines der Zufallsexperiment zuvor mit Infektion beschrieben wird, soll eine 1 ausgeworfen werden.
| Person 5 |
|---|
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 0 |
| 1 |

Gefährdungsfunktion mittels GeoGebra
[Bearbeiten]Normalverteilung:
d und c
- d = Integral(p(x), -j, j)
- c = 1-d (Infektionswahrscheinlichkeit)

Modellierung Klassenzimmer mit Gefährdungsfunktion in Octave
[Bearbeiten]Festlegung grundlegender Variablen und Bedingungen
[Bearbeiten]clear all close all % Anzahl der bewegenden Personen PersonenX=5; % Personen insgesamt in x PersonenY=5; % Personen insgesamt in y Zeitschritte=2; T=2;
% Fuer die Gefaehrdungsfunktion werden globale Variablen definiert um sie in anderen Funktionen nutzen zu koennen. % Deinition einer Normalverteilung mit sigma entsprechend der Funktionsvorschrift global sigma = 0.6; global f = @(t) 1/sqrt(2*pi*sigma.^2)*exp(-1/2*(t/sigma).^2);
% Definition Menschen % Definieren auf Basis des Szenarios % Ausgangsposition - jeder im Abstand von 2m zu einer anderen Person Abstand=2; x=[1:Abstand:PersonenX*Abstand]; y=[1:Abstand:PersonenY*Abstand]; [X,Y]=meshgrid(x,y);
% Definition der Raender auf Basis der Personen (Vektoren x und y)
xMin=x(1)-1;
xMax=x(end)+1;
yMin=y(1)-1;
yMax=y(end)+1;
% Gibt an, was passiert, wie weit sich eine Person von der Wand wegbewegt, sofern sie auf sie trifft
Faktor=1;
Abstandsvektor=[]
%X=[2,5,8];
%Y=[5,7,9];
Erster Infizierter
[Bearbeiten]% Position des ersten Infizierten wird durch ein Zufallsexperiment bestimmt % Indices der Person wird herausgegeben % rand(1) gibt eine Zufallszahl zwischen 0 und 1 heraus xZufall=ceil(PersonenX*rand(1)); yZufall=ceil(PersonenY*rand(1));
% geometrische Position der Infizierten Person wird auf Basis der Indices ermittelt
XInf=X(yZufall,xZufall)
YInf=Y(yZufall,xZufall)
% Erste Infizierte Person wird in die Vektoren der Infizierten Personen übernommen InfizierteX=[xZufall]; InfizierteY=[yZufall]; InfizierteXneu=InfizierteX; % Dient als Zwischenspeicher InfizierteYneu=InfizierteY; % Dient als Zwischenspeicher
Plot Ausgangssituation
[Bearbeiten]% Erster Plot
figure(1)
plot(X,Y,'*b')
hold on
axis([x(1)-10 x(end)+10 y(1)-10 y(end)+10])
plot(XInf,YInf,'sr')
hold off

Bewegung der Personen
[Bearbeiten]% Bewegung % Bewegungsvektoren fuer das erste T wird erstellt VPosX=rand(PersonenY,PersonenX)-0.5; VPosY=rand(PersonenY,PersonenX)-0.5; for i=1:Zeitschritte*T neuX=X+VPosX; neuY=Y+VPosY; for k1=1:PersonenX for k2=1:PersonenY % Abfragen, ob sich eine Person aus dem definierten Gebiet herausbewegt % Sollte dies passieren, wird sie mittels Zufallsexperiment von der Wand entfernt und % in das Gebiet zurueckgeschickt. if neuX(k2,k1)<xMin neuX(k2,k1)=X(k2,k1)+rand(1)*Faktor; elseif neuX(k2,k1)<xMin && neuY(k2,k1)<yMin % Abfrage wo die Person den Rand ueberschreitet neuX(k2,k1)=X(k2,k1)+rand(1)*Faktor; % Abhaengig von dieser Abfrage wird die Person vom Rand neuY(k2,k1)=Y(k2,k1)+rand(1)*Faktor; % weggeschickt elseif neuX(k2,k1)<xMin && neuY(k2,k1)>yMax neuX(k2,k1)=X(k2,k1)+rand(1)*Faktor; neuY(k2,k1)=Y(k2,k1)-rand(1)*Faktor; elseif neuX(k2,k1)>xMax neuX(k2,k1)=X(k2,k1)-rand(1)*Faktor; elseif neuX(k2,k1)>xMax && neuY(k2,k1)<yMin neuX(k2,k1)=X(k2,k1)-rand(1)*Faktor; neuY(k2,k1)=Y(k2,k1)+rand(1)*Faktor; elseif neuX(k2,k1)>xMax && neuY(k2,k1)>yMax neuX(k2,k1)=X(k2,k1)-rand(1)*Faktor; neuY(k2,k1)=Y(k2,k1)-rand(1)*Faktor; elseif neuY(k2,k1)<yMin neuY(k2,k1)=Y(k2,k1)+rand(1)*Faktor; elseif neuY(k2,k1)>yMax neuY(k2,k1)=Y(k2,k1)-rand(1)*Faktor; else X(k2,k1)=neuX(k2,k1); Y(k2,k1)=neuY(k2,k1); endif endfor endfor X=neuX; Y=neuY;
Plot der Bewegung
[Bearbeiten]figure(i+10)
plot(neuX,neuY,'*b')
hold on
axis([x(1)-10 x(end)+10 y(1)-10 y(end)+10])
Rahmen plotten
plot([xMin xMin],[yMin yMax],"-b");
plot([xMax xMax],[yMin yMax],"-b");
plot([xMin xMax],[yMin yMin],"-b");
plot([xMin xMax],[yMax yMax],"-b");
%quiver(neuX,neuY,VPosX,VPosY); %Sofern Bewegungspfeile gewuenscht % Zu jedem neuen T wird die Bewegungsrichtung der Personen gewechselt if mod(i,Zeitschritte)==0 VPosX=rand(PersonenY,PersonenX)-0.5; VPosY=rand(PersonenY,PersonenX)-0.5; endif
Infektion
[Bearbeiten]% Definition Ansteckungsfunktion function [Infektion]=Ansteckungsfunktion(Abstand) % Globale Variablen(Normalverteilung mit entsprechenden Paramaetern) werden involviert global sigma global f % Siehe GeoGebra fuer Erklaerung Infwahrscheinlichkeit=1-integral(f,-Abstand,Abstand); % Zufallsexperiment wird durchgefuert % Entscheidung fuer eine Infektion oder nicht Experiment=rand(1); if Experiment<Infwahrscheinlichkeit Infektion=true; else Infektion=false; endif endfunction
Abstandscheck und neue Infizierungen
[Bearbeiten]for j=1:columns(InfizierteX) % Abstand zu jedem Infizierten wird berechnet for k1=1:PersonenX % Alle Personen werden "durchiteriert" for k2=1:PersonenY % Abstandsabgleich zum Infizierten von jeder Person Abstand=norm([neuX(k2,k1)-neuX(InfizierteY(j),InfizierteX(j)),neuY(k2,k1)-neuY(InfizierteY(j),InfizierteX(j))]); % Gefahrfunktion und Zufallexperiment Infektion=Ansteckungsfunktion(Abstand); if Infektion==true % Ansteckungsfunktion Abstandsvektor=[Abstandsvektor,Abstand]; % Neu infizierte Person wird in den Speicher übernommen InfizierteXneu=[InfizierteXneu k1]; InfizierteYneu=[InfizierteYneu k2]; % Speicheroptimierung - Personen sollen nicht doppelt im Speicher der Infizierten vorkommen A1 = [InfizierteXneu']; A2 = [InfizierteYneu']; A=[A1,A2]; B=unique(A,"rows"); InfizierteXneu=B(:,1)'; InfizierteYneu=B(:,2)'; endif endfor endfor endfor
% Zwischenspeicheruebergabe
InfizierteX=InfizierteXneu;
InfizierteY=InfizierteYneu;
% Kennzeichnung aller Infizierten
for l=1:columns(InfizierteX)
plot(neuX(InfizierteY(l),InfizierteX(l)),neuY(InfizierteY(l),InfizierteX(l)),'sr')
endfor
endfor
Verbesserungsvorschläge
[Bearbeiten]% Reflexion an der Wand % Nach einer bestimmten Anzahl von Zeitschritten wird eine Person aus dem Infiziertenspeicher % geloescht und in die Gruppe der Genesenen % Einzelne Personen bewegen sich schneller oder langsamer % Szenarios von Gruppenbildung % Abaenderung der Gefahrenfunktion
Kontinueliche Modellierung
[Bearbeiten]Tutorium 1 - Kontaktmodell
[Bearbeiten]%Anzahl von Punkten in x- und y-Richtung Nx=10; Ny=20; radiusInf=0.8; Zeitschritte=3; %pro eine Zeiteinheit T=1 T=6; %Die Berechnung wird für 5 Zeiteinheiten laufen g=0.5;% Geschwindigkeit mit der sich die Fußgänger fortbewegen Anzahl=[1];
x=[1:Nx]; y=[1:Ny]; dt=1/Zeitschritte;
[x,y]=meshgrid (x,y);
%erste infizierte Person xInf=x(1, Nx/2); yInf=y(Ny/2); IndInf2=Nx/2; %Spalte IndInf1=Ny/2; %Zeile IndInf1neu=IndInf1; IndInf2neu=IndInf2; Plot figure (1) hold on; plot(x,y, '*b') ; plot(xInf,yInf, 'sr') ; axis([-5 15 -5 25]);
%mit folgenden Befehlen kann man die Bilder speichern und für weitere Bearbeitung verwenden (Videos, Animationen)
%test=["Fig_", num2str(1),".jpg"]
%saveas(1, test)
hold off;

for i=1:T*Zeitschritte %1. Zeiteinheit
figure (i+1) title (['t=' num2str(i*dt)]) axis([-5 15 -5 25]); hold on
% Zielpunkt, der am Ende der Bewegung erreicht werden soll
% Mit rand(Ny,Nx) wird eine Matrix generiert - es entstehen Zufallszahlen zwischen -0.5 und 0.5
% Zielpositionen werden durch Addition der Zufallszahlen zwischen -0.5 und 0.5 zu jeder x,y-Koordinate generiert und mit der Geschwindigkeit g skaliert
neuPosX=x.+g.*rand(Ny,Nx)-0.5*g; neuPosY=y.+g.*rand(Ny,Nx)-0.5*g;
%In jedem Zeitschritt wird zur aktuellen Position ein Bruchteil i*dt der noch ausstehenden Strecke addiert
Faktor=mod(i,Zeitschritte);
if Faktor==0
Faktor=Zeitschritte;
endif
neuX=x.+1*(neuPosX.-x)*Faktor*dt; neuY=y.+1*(neuPosY.-y)*Faktor*dt;
VPosX=neuX.-x; VPosY=neuY.-y;
x=neuX; y=neuY;
%%neue Infizierungen: %%In Vektoren IndInf1, IndInf2 sind die i- und j-Indexen der (x,y)-Koordinaten der bereits Infizierten gespeichert. %%---------------------------
for k1=1:length(IndInf1)
for j=1:Nx
for l=1:Ny
%%die aktuellen Positionen der Fußgänger-Punkte werden mit den Positionen der Infizierten abgeglichen (Abstand wird berechnet)
abstand=norm ( [neuX(l,j)-neuX(IndInf1(k1),IndInf2(k1)), neuY(l,j)-neuY(IndInf1(k1),IndInf2(k1))]);
if abstand<radiusInf
%%wenn der Abstand zum Infizierten unter dem Ansteckungsradius liegt, wird der l,j-te Punkt infiziert (mit rotem Quadrat gekennzeichnet)
abstand;
plot(neuX(l,j),neuY(l,j), 'sr') ;
hold on
%%---------------------------
k2=1;
%% der Vektor der Infizierten wird untersucht, falls die l,j-Indexen des aktuellen Punkten nicht unter den
%infizierten Indexen auftauchen, werden die l,j-Indexen des aktuell Infizierten zu den neuen Vektoren der Infizierten-Indexen
% IndInf1neu, IndInf2neu zugefügt.
%(Grund: Speicheroptimierung)
while k2 <=length(IndInf1)&&(l!=IndInf1neu(k2) || j!=IndInf2neu(k2))
k2=k2+1;
endwhile
if k2 >length(IndInf1)
IndInf1neu=[IndInf1neu l];
IndInf2neu=[IndInf2neu j];
endif
endif
endfor
endfor
endfor
IndInf1=IndInf1neu; IndInf2=IndInf2neu;
Laenge=length(IndInf1) Anzahl= [Anzahl, Laenge];
plot(neuX,neuY, '*b') quiver (neuX,neuY, VPosX,VPosY); %%Speichern der Bilder: optional %test=["Fig_", num2str(i+1),".jpg"] %saveas(i+1, test) hold off %% Erreichte Position wird nach einem Zeitschritt i in x bzw. y gespeichert endfor

%%Zeitschleife abgeschlossen %%--------------------------- figure (20) hold on plot([0,(1:T*Zeitschritte)*dt], Anzahl, 'sr-') xlabel('Zeit') ylabel('Anzahl von Infizierten') grid on %test=["Fig_", num2str(20),".jpg"] %saveas(20, test)

Das Kontaktmodell soll zunächst dazu dienen ein vereinfachtes Modell der Verbreitung einer COVID-19 Infektion darzustellen. Dabei stehen die Punkte, welche durch eine Matrix gebildet wurden, für Personen. In der Ausgangssituation sind 200 Personen abgebildet. Der Infizierte befindet sich in der Mitte und wird durch ein rotes Quadrat markiert. Die Passanten bewegen sich zunächst mit einer Geschwindigkeit von 0,5 km/h in unterschiedliche Richtungen. Bei einem Abstand unter 0,8 m zu einer Infizierten Person wird ein weiterer Passant infiziert, der in den Radius des Infizierten eintritt. Mit der Abänderung unterschiedlicher Faktoren, die auf das Modell einwirken, können Beobachtungen bezüglich Veränderungen der Verbreitung wahrgenommen werden. Diese sollen im Folgenden dokumentiert werden.
Ausgangssituation
[Bearbeiten]
Veränderung des Ansteckungsradius
[Bearbeiten]
Zunächst wurde der Ansteckungsradius verändert. Dabei wurde der Radius des Infizierten, in der diese Person für andere ansteckend ist, auf 1,3 m erhöht. Mit der Vergrößerung des Radius steigt die Anzahl der Infizierten und die Infektion kann sich schneller ausbreiten. Modellhaft kann man von einer ansteckenderen Mutation der Infektion ausgehen.
Erhöhung der Geschwindigkeit
[Bearbeiten]
Die Geschwindigkeit wurde im Modell von 0,5 km/h auf 1 km/h erhöht. Eine erhöhte Geschwindigkeit bringt zunächst ebenfalls eine höhere Infektionszahl mit sich. Da sich die Passanten allerdings immer weiter voneinander entfernen treten weniger Verbindungen zwischen den Passanten auf. Dadurch steigen die Infektionen bei erhöhten Zeitschritten nicht mehr an.
Veränderung der Zeiteinheiten
[Bearbeiten]
Erhöht man die Zeitschritte von 3 auf 5, ist eine niedrigere Anzahl der Infizierten in einem Zeitschritt zu beobachten, da sich der Vorgang über einen längeren Zeitraum vollstreckt.
Wahl des ersten Infizierten als Randpunkt
[Bearbeiten]
Nun wird der erste Infizierte nicht im Zentrum der Matrix gewählt, sondern als Randpunkt, genauer noch als Eckpunkt. Hier wird keine weitere Person Infiziert, da sich der Ausgangspunkt der Infektion direkt von den anderen Personen entfernt und dadurch keine Kontakte entstehen können.
Erhöhung des Ansteckungsradius und Geschwindigkeitsreduktion
[Bearbeiten]
Die Geschwindigkeit wird von 0,5 km/h auf 0,2 km/h reduziert und der Ansteckungsradius auf 1,2 m erhöht. Die Anzahl der Infektionen steigt noch schneller wie zuvor an. Die Passanten entfernen sich durch die geringere Geschwindigkeit viel langsamer voneinander und werden zudem durch den erhöhten Ansteckungsradius schneller mit COVID-19 infiziert.
Tutorium 2 - Fundamenallösungen der Diffusionsgleichung
[Bearbeiten]Stationäre Diffusion: Laplace Gleichung ⇒ Fundamentallösung von Phi
[Bearbeiten]clear all;
x=[-2:0.08:-0.01,0.01:0.08:2]; %Singularität rausnehmen (denn wenn wir Werte gegen Null schicken, geht das Ganze gegen unendlich)
y=[-2:0.08:-0.01,0.01:0.08:2];
[x,y]=meshgrid(x,y); %Matrizen werden erzeugt
Formel der Fundamentallösung der Laplace-Gleichung für:
u=(-1/(2*pi))*log(sqrt(x.^2+y.^2)); %Laplace-Gleichung auf R^2
Plot
figure(1)
meshc(x,y,u)
title('Graphische Darstellung der Laplace Gleichung auf R^2')

Stationäre Diffusion: Poisson Gleichung
[Bearbeiten]function wert=Quellfunktion(x,y) if sqrt((x.-1.0).^2+(y.-1).^2)<=0.15 wert=1; else wert=0; if sqrt((x.-4.0).^2+(y.-2).^2)<=0.15 wert=0.5; else wert=0; %+. endif endif endfunction
Rechteckiges Gebiet/Gitter wird definiert
step=0.03;
X=[0:step:5];
Y=[0:step:5]; %Hier wurde das Rechteck verändert, über das integriert wird, sodass beide Träger mit drin sind (Aufgabe 2a).
[x,y]=meshgrid(X,Y);
Auswertung der Quellfunktion in allen Punkten des Gitters
for i=1:(length(X))
for j=1:(length(Y))
f(j,i)=1*Quellfunktion(x(j,i),y(j,i)); %Auswertung wird in f gespeichert
endfor
endfor
Implementierung der Poissonformel
[Bearbeiten]for i=1:(length(X)) for j=1:(length(Y)) xstar=x(j,i)*ones(length(Y),length(X)); ystar=y(j,i)*ones(length(Y),length(X)); % Phi mit verschobenem Argument: phi=-log(sqrt((xstar.-x).^2+(ystar.-y).^2))/(2*pi); phi(j,i)=0; %numerische Integration I(j,i) = trapz(Y,trapz(X,phi.*f,2)); endfor endfor
Graphische Ausgaben
figure 1
meshc(x,y,I)
grid on
title ('Losung von Poissongleichung')
xlabel('x')
ylabel ('y')
figure 2
surfc(x,y,f)
title ('Funktion der rechten Seite')


Zeitabhängige Diffusion ⇒ Fundamentallösung von Psi
[Bearbeiten]close all clear all Abmessung=3; %Damit wir den Anfangs- und Endwert schneller abändern können, definieren wir "Abmessung" Schrittweite=0.1; %Gleiches erfolgt mit der Schrittweite %Ausschneiden des Punktes (0,0) nicht notwendig, da die Singularität in diesem Fall nur entsteht wenn alles 0 ist - x, z aber auch t, was hier nicht so ist. x=[-Abmessung:Schrittweite:Abmessung]; y=[-Abmessung:Schrittweite:Abmessung]; [x,y]=meshgrid(x,y); %Matrizen werden erzeugt
norm=sqrt(x.^2+y.^2); %Norm wird definiert, sodass wir sie in z verwenden können
% Diffusionskoeffizienten a=0.1; %Je größer a ist, desto schneller bewegen sich die Teilchen von Ort hoher Konzentration, zu Ort niedriger Konzentration
t0=0.01 dt=0.2
for k=0:5 %hier definieren wir eine for-Schleife für die verschiedenen Zeitpunkte. Diese läuft von Zeitpunkt t1 bis t5.
t=t0+k*dt;
Lösungsformel für die homogene (instationäre) Diffusionsgeichung für konstanten Diffusionskoeffizient
.
z=(1/(4*pi*a*t))*exp(-norm.^2/(4*a*t)); %stationaere Diffusionsgleichung für n=2
%plotten figure(k+1) %Plott soll zum jeweiligen Zeitpunkt k+1 folgen meshc(x,y,z) grid on title (['Loesung von Diffusionsgleichung_',num2str(k)]) %num2str führt dazu, dass die bei allen Bildern der Zeitpunkt angegeben wird. xlabel('x') ylabel ('y') axis([-Abmessung Abmessung -Abmessung Abmessung 0 6.48]) %Achsen werden fest gewählt, sodass die Bilder aussagekräftig sind und nicht immer anders skaliert sind %Skalierung der Achsen: x-Werte von -2 bis +2; y-Werte von -2 bis +2 und z-Werte von 0 bis 6.48
% Speichern der Bilder
filename=["Images/Figure_" num2str(k+1) ".jpg"]; %[] texte werden verbunden ; num2str = Nummer zu Text; / = in dem Ordner speichern! mehrere / in den jeweiligen Unterordner
saveas(k+1,filename)
endfor
Zeitabhängige Diffusion als Anfangswertproblem
[Bearbeiten]clear all
function wert=Quellfunktion(x,y) %Quellfunktion wird definiert (wie ganz oben)
if sqrt((x.-1.0).^2+(y.-1).^2)<=0.15 wert=1;
else wert=0;
if sqrt((x.+1.0).^2+(y.+1).^2)<=0.15 wert=1;
else wert=0;
endif
endif
endfunction
% Langsamere Diffusionsgeschwindigkeit
a=1;
step=0.05; %Abstand der Gitterpunkte
%x und y Matrizen werden definiert
Abmessungen=2;
X=[-Abmessungen:step:Abmessungen];
Y=[-Abmessungen:step:Abmessungen];
[x,y]=meshgrid(X,Y);
%Quellfunktion wird in einer Schleife für i von i=1 bis zur jeweiligen Länge des Vektors x bzw. y aufgerufen for i=1:(length(X)) for j=1:(length(Y)) f(j,i)=1*Quellfunktion(x(j,i),y(j,i)); %Speichern erfolgt in Matrix f an der Stelle (j,i) endfor endfor %Anfangsloesung-Darstellung meshc(x,y,f)

%Zeitschleife für t wird eingebaut for t=0.08:0.02:0.16 %wir fangen bei 0,08 an und laufen in 0,02er Schritten zu 0,16
%man geht in 2 for-Schleifen über alle Gitterpunkte
for i=1:(length(X))
for j=1:(length(Y))
%________________ xstar=x(j,i)*ones(length(Y),length(X)); ystar=y(j,i)*ones(length(Y),length(X)); % Psi mit verschobenem Argument: psi=(1/(4*pi*a*t))*exp(-((xstar.-x).^2+(ystar.-y).^2)/(4*a*t));
%numerische Integration J(j,i) = trapz(Y,trapz(X,psi.*f,2)); %wird in Matrix J gespeichert %_______________
endfor endfor
%plotten n_fig=1000+t*1000; figure(n_fig) meshc(x,y,J) title(['Loesung zeitabhaengige Diffusionsgleichung' num2str(t)]) xlabel('x-Achse') ylabel('y-Achse') axis([-0.8 2 -0.8 2 0 1.0]) %Achsen werden fest gewählt, sodass die Bilder aussagekräftig sind und nicht immer anders skaliert sind
endfor
Tutorium 3 - Modifiziertes SIR Modell
[Bearbeiten]Parameter des SIR Models
[Bearbeiten]NM=55000; % Kapazitätsgrenze, 2/3 der deutschen Bevölkerung (in T)
c=0.32450; % Basisinfektionsrate- die Rate des exponenziellen Wachstums am Anfang der Pandemie w=1/13.90; % Wechselrate zu den Genesenen d=0.003; % Todesrate
% Anteil der erfassten Infizierten r=0.1; %Veraenderung des r-Werts - Aufgabe 3 r=[0.1:0.1:1];
Aktuelle Daten bis zum 02.06.21 function y= Daten() infects = [ 16.0 18.0 21.0 26.0 53.0 66.0 117.0 150.0 188.0 240.0 400.0 639.0 795.0 902.0 1139.0 1296.0 1567.0 2369.0 3062.0 3795.0 4838.0 6012.0 7156.0 8198.0 10999.0 13957.0 16662.0 18610.0 22672.0 27436.0 31554.0 36508.0 42288.0 48582.0 52547.0 57298.0 61913.0 67366.0 73522.0 79696.0 85778.0 91714.0 95391.0 99225.0 103228.0 108202.0 113525.0 117658.0 120479.0 123016.0 125098.0 127584.0 130450.0 133830.0 137439.0 139897.0 141672.0 143457.0 145694.0 148046.0 150383.0 152438.0 154175.0 155193.0 156337.0 157641.0 159119.0 160758.0 161703.0 162496.0 163175.0 163860.0 164807.0 166091.0 167300.0 168531.0 169218.0 169575.0 170508.0 171306.0 172239.0 173152.0 173772.0 174355.0 174697.0 175210.0 176007.0 176752.0 177212.0 177850.0 178281.0 178570.0 179002.0 179364.0 179717.0 180458.0 181196.0 181482.0 181815.0 182028.0 182370.0 182764.0 183271.0 183678.0 183979.0 184193.0 184543.0 184861.0 185416.0 185674.0 186022.0 186269.0 186461.0 186839.0 187184.0 187764.0 188534.0 189135.0 189822.0 190359.0 190862.0 191449.0 192079.0 192556.0 193243.0 193499.0 193761.0 194259.0 194725.0 195228.0 195674.0 196096.0 196335.0 196554.0 196944.0 197341.0 197783.0 198178.0 198556.0 198804.0 198963.0 199375.0 199726.0 200260.0 200843.0 201372.0 201574.0 201823.0 202345.0 202799.0 203368.0 204183.0 204964.0 205269.0 205609.0 206242.0 206926.0 207828.0 208698.0 209653.0 209893.0 210402.0 211281.0 212022.0 213067.0 214214.0 215336.0 215891.0 216327.0 217293.0 218519.0 219964.0 221413.0 222828.0 223453.0 224014.0 225404.0 226914.0 228621.0 230048.0 232082.0 232864.0 233575.0 234853.0 236429.0 237936.0 239507.0 240986.0 241771.0 242381.0 243599.0 244855.0 246166.0 247619.0 248997.0 249985.0 250799.0 252298.0 253474.0 255366.0 256850.0 258480.0 259428.0 260355.0 261762.0 263663.0 265857.0 267773.0 270070.0 271415.0 272337.0 274158.0 275927.0 278070.0 280223.0 282730.0 284140.0 285332.0 287421.0 289219.0 291722.0 294395.0 296958.0 299237.0 300619.0 303258.0 306086.0 310144.0 314660.0 319381.0 322864.0 325331.0 329453.0 334585.0 341223.0 348557.0 356387.0 361974.0 366299.0 373167.0 380762.0 392049.0 403291.0 418005.0 429181.0 437866.0 449275.0 464239.0 481013.0 499694.0 518753.0 532930.0 545027.0 560379.0 577593.0 597583.0 619089.0 642488.0 658505.0 671868.0 687200.0 705687.0 727553.0 751095.0 773556.0 790503.0 801327.0 815746.0 833307.0 855916.0 879564.0 902528.0 918269.0 929133.0 942687.0 961320.0 983588.0 1006394.0 1028089.0 1042700.0 1053869.0 1067473.0 1084743.0 1106789.0 1130238.0 1153556.0 1171323.0 1183655.0 1197709.0 1218524.0 1242203.0 1272078.0 1300516.0 1320716.0 1337078.0 1351510.0 1379238.0 1406161.0 1439938.0 1471238.0 1494009.0 1510652.0 1530180.0 1554920.0 1587115.0 1587115.0 1627103.0 1640858.0 1651834.0 1664726.0 1687185.0 1719737.0 1719737.0 1755351.0 1765666.0 1775513.0 1787410.0 1808647.0 1835038.0 1866887.0 1891581.0 1908527.0 1921024.0 1933826.0 1953426.0 1978590.0 2000958.0 2019636.0 2033518.0 2040659.0 2052028.0 2068002.0 2088400.0 2106262.0 2122679.0 2134936.0 2141665.0 2148077.0 2161275.0 2178828.0 2192850.0 2205171.0 2216363.0 2221971.0 2228085.0 2237790.0 2252001.0 2264909.0 2275394.0 2284010.0 2288545.0 2291924.0 2299996.0 2310233.0 2320093.0 2328447.0 2334561.0 2338987.0 2342843.0 2350399.0 2360606.0 2369719.0 2378883.0 2386559.0 2390928.0 2394811.0 2402818.0 2414687.0 2424684.0 2434446.0 2442336.0 2447068.0 2451011.0 2460030.0 2471942.0 2482522.0 2492079.0 2500182.0 2505193.0 2509445.0 2518591.0 2532947.0 2545781.0 2558455.0 2569245.0 2575849.0 2581329.0 2594764.0 2612268.0 2629750.0 2645783.0 2659516.0 2667225.0 2674710.0 2690523.0 2713180.0 2734753.0 2755225.0 2772401.0 2782273.0 2791822.0 2808873.0 2833173.0 2855061.0 2873190.0 2885386.0 2893883.0 2900768.0 2910445.0 2930852.0 2956316.0 2980413.0 2998268.0 3011513.0 3022323.0 3044016.0 3073442.0 3099273.0 3123077.0 3141262.0 3153699.0 3163308.0 3188192.0 3217710.0 3245253.0 3268645.0 3287418.0 3299325.0 3310301.0 3332532.0 3357268.0 3381597.0 3400532.0 3416822.0 3425982.0 3433516.0 3451550.0 3473503.0 3491988.0 3507673.0 3520329.0 3527251.0 3533376.0 3548285.0 3565704.0 3577040.0 3584934.0 3593434.0 3598846.0 3603055.0 3614095.0 3626393.0 3635162.0 3642244.0 3648958.0 3651640.0 3653551.0 3656177.0 3662490.0 3669870.0 3675296.0 3679148.0 3681126.0 3682911.0 3687828.0 ]; deads = [ 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 12.0 20.0 31.0 46.0 55.0 86.0 114.0 149.0 198.0 253.0 325.0 389.0 455.0 583.0 732.0 872.0 1017.0 1158.0 1342.0 1434.0 1607.0 1861.0 2107.0 2373.0 2544.0 2673.0 2799.0 2969.0 3254.0 3569.0 3868.0 4110.0 4294.0 4404.0 4598.0 4879.0 5094.0 5321.0 5500.0 5640.0 5750.0 5913.0 6115.0 6288.0 6481.0 6575.0 6649.0 6692.0 6831.0 6996.0 7119.0 7266.0 7369.0 7395.0 7417.0 7533.0 7634.0 7723.0 7824.0 7881.0 7914.0 7935.0 8007.0 8090.0 8147.0 8174.0 8216.0 8247.0 8257.0 8302.0 8349.0 8411.0 8450.0 8489.0 8500.0 8511.0 8522.0 8551.0 8581.0 8613.0 8646.0 8668.0 8674.0 8711.0 8729.0 8755.0 8763.0 8781.0 8787.0 8791.0 8800.0 8830.0 8856.0 8872.0 8883.0 8882.0 8885.0 8895.0 8914.0 8927.0 8948.0 8954.0 8957.0 8961.0 8973.0 8985.0 8994.0 9003.0 9010.0 9012.0 9016.0 9024.0 9036.0 9048.0 9054.0 9060.0 9063.0 9064.0 9068.0 9071.0 9078.0 9082.0 9083.0 9084.0 9086.0 9090.0 9095.0 9101.0 9111.0 9118.0 9118.0 9118.0 9122.0 9128.0 9134.0 9141.0 9148.0 9141.0 9148.0 9156.0 9168.0 9175.0 9183.0 9195.0 9196.0 9197.0 9201.0 9207.0 9211.0 9225.0 9231.0 9231.0 9232.0 9236.0 9243.0 9253.0 9260.0 9267.0 9269.0 9272.0 9277.0 9280.0 9285.0 9288.0 9289.0 9295.0 9298.0 9302.0 9313.0 9321.0 9322.0 9324.0 9325.0 9325.0 9329.0 9338.0 9341.0 9342.0 9347.0 9349.0 9350.0 9362.0 9368.0 9371.0 9378.0 9384.0 9386.0 9386.0 9396.0 9409.0 9428.0 9443.0 9452.0 9457.0 9460.0 9471.0 9488.0 9500.0 9508.0 9527.0 9529.0 9534.0 9546.0 9562.0 9578.0 9589.0 9604.0 9615.0 9621.0 9634.0 9677.0 9710.0 9734.0 9767.0 9777.0 9789.0 9836.0 9875.0 9905.0 9954.0 10003.0 10032.0 10056.0 10098.0 10183.0 10272.0 10349.0 10452.0 10481.0 10530.0 10661.0 10812.0 10930.0 11096.0 11226.0 11289.0 11352.0 11506.0 11767.0 11982.0 12200.0 12378.0 12485.0 12547.0 12814.0 13119.0 13370.0 13630.0 13884.0 14022.0 14112.0 14361.0 14771.0 15160.0 15586.0 15965.0 16123.0 16248.0 16636.0 17123.0 17602.0 18034.0 18517.0 18772.0 18919.0 19342.0 19932.0 20372.0 20970.0 21466.0 21787.0 21975.0 22475.0 23427.0 24125.0 24938.0 25640.0 26049.0 26275.0 27006.0 27968.0 28770.0 28770.0 29422.0 29778.0 30126.0 30978.0 32107.0 33071.0 33071.0 33960.0 34272.0 34574.0 35518.0 36537.0 37607.0 38795.0 39878.0 40343.0 40686.0 41577.0 42637.0 43881.0 44994.0 45974.0 46419.0 46633.0 47622.0 48770.0 49783.0 50642.0 51521.0 51870.0 52087.0 52990.0 53972.0 54913.0 55752.0 56546.0 56945.0 57120.0 57981.0 58956.0 59742.0 60597.0 61286.0 61517.0 61675.0 62156.0 62969.0 63635.0 64191.0 64742.0 64960.0 65076.0 65604.0 66164.0 66698.0 67206.0 67696.0 67841.0 67903.0 68318.0 68740.0 69125.0 69519.0 69888.0 70045.0 70105.0 70463.0 70881.0 71240.0 71504.0 71804.0 71900.0 71934.0 72189.0 72489.0 72810.0 73062.0 73301.0 73371.0 73418.0 73656.0 73905.0 74132.0 74358.0 74565.0 74664.0 74714.0 74964.0 75212.0 75440.0 75623.0 75780.0 75870.0 75913.0 76093.0 76342.0 76543.0 76775.0 76895.0 76963.0 77013.0 77103.0 77401.0 77707.0 78003.0 78249.0 78353.0 78452.0 78746.0 79088.0 79381.0 79628.0 79847.0 79914.0 80006.0 80303.0 80634.0 80893.0 81158.0 81444.0 81564.0 81624.0 81968.0 82280.0 82544.0 82850.0 83082.0 83192.0 83276.0 83591.0 83876.0 84126.0 84410.0 84648.0 84775.0 84829.0 85112.0 85380.0 85658.0 85848.0 86025.0 86096.0 86160.0 86381.0 86665.0 86902.0 87128.0 87298.0 87380.0 87423.0 87456.0 87726.0 87995.0 88187.0 88350.0 88406.0 88442.0 88595.0 88774.0]; recovered = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 0.0, 13500.0, 16100.0, 18700.0, 21400.0, 23800.0, 26400.0, 28700.0, 30600.0, 33000.0, 46300.0, 49000.0, 53913.0 57400.0 60200.0 64300.0 68200.0 72600.0 77000.0 81800.0 85400.0 88000.0 91500.0 95200.0 99400.0 103300.0 106800.0 109800.0 112000 114500 117400.0 120400.0 123500.0 126900.0 129000.0 130600.0 132700.0 135100.0 137400.0 139900.0 141700.0 143300.0 144400.0 145600.0 147200.0 148700.0 150300.0 151700.0 152600.0 153400.0 154600.0 155700.0 156900.0 158000.0 159000.0 159900.0 160300.0 161200.0 162000.0 162800.0 163200.0 164100.0 164900.0 165200.0 165900.0 166400.0 167300.0 167800.0 168500.0 168900.0 169100.0 169600.0 170200.0 170700.0 171200.0 171600.0 171900.0 172200.0 172600.0 173100.0 173600.0 174100.0 174400.0 174700.0 174900.0 175300.0 175700.0 176300.0 176800.0 177100.0 177500.0 177700.0 178100.0 179100.0 179800.0 180300.0 181000.0 181300.0 181700.0 182200.0 182700.0 183100.0 183600.0 184000.0 184400.0 184600.0 185100.0 185500.0 186000.0 186400.0 186900.0 187200.0 187400.0 187800.0 188100.0 188600.0 189000.0 189400.0 189800.0 190000.0 190400.0 190800.0 191300.0 191800.0 192300.0 192700.0 192900.0 193500.0 194000.0 194600.0 195200.0 195900.0 196400.0 196800.0 197400.0 198100.0 198800.0 199500.0 200200.0 200800.0 201300.0 202100.0 203000.0 203900.0 204800.0 205800.0 206600.0 207100.0 208200.0 209300.0 210600.0 211900.0 213200.0 214200.0 214900.0 216200.0 217600.0 219100.0 220500.0 221900.0 222900.0 223700.0 225000.0 226500.0 228000.0 229400.0 230600.0 231400.0 232100.0 233300.0 234600.0 236000.0 237300.0 238700.0 239800.0 240700.0 242200.0 243700.0 245400.0 246900.0 248500.0 249700.0 250500.0 252500.0 254200.0 256000.0 257900.0 259500.0 260900.0 261900.0 263700.0 265600.0 267700.0 269600.0 271800.0 273500.0 274800.0 276900.0 279300.0 281900.0 284600.0 287600.0 290000.0 291900.0 294800.0 298300.0 302100.0 306100.0 310300.0 314100.0 317100.0 321600.0 326700.0 332800.0 339200.0 345700.0 351200.0 355900.0 363100.0 371500.0 381400.0 391600.0 402500.0 412000.0 419300.0 429600.0 441200.0 454800.0 467800.0 481700.0 493200.0 502300.0 515200.0 530200.0 546500.0 562700.0 579100.0 593100.0 603800.0 618800.0 636700.0 656400.0 676100.0 696100.0 711000.0 722300.0 739100.0 758800.0 779500.0 800000.0 820600.0 835700.0 846400.0 863300.0 881800.0 902100.0 922100.0 942100.0 957500.0 967900.0 984200.0 1003300.0 1025000.0 1047600.0 1069400.0 1085500.0 1097400.0 1115400.0 1136700.0 1160100.0 1184400.0 1184400.0 1223700.0 1236700.0 1255700.0 1277900.0 1302600.0 1328200.0 1328200.0 1368100.0 1381900.0 1401200.0 1424700.0 1451000.0 1474000.0 1494100.0 1511800.0 1525300.0 1545500.0 1570000.0 1596600.0 1620200.0 1641200.0 1657900.0 1672000.0 1691700.0 1716200.0 1741800.0 1762200.0 1780200.0 1795400.0 1807500.0 1823500.0 1844000.0 1866000.0 1883700.0 1898900.0 1911800.0 1921700.0 1935600.0 1954000.0 1973200.0 1991000.0 2008200.0 2020900.0 2029200.0 2041300.0 2057300.0 2073100.0 2087600.0 2101000.0 2112000.0 2119100.0 2128800.0 2141400.0 2154600.0 2165900.0 2176300.0 2185100.0 2190600.0 2198000.0 2207700.0 2217700.0 2226500.0 2235700.0 2243200.0 2248400.0 2255500.0 2264600.0 2274400.0 2283400.0 2292100.0 2299400.0 2304300.0 2310900.0 2319600.0 2328700.0 2337000.0 2345600.0 2352600.0 2358000.0 2365100.0 2374200.0 2383600.0 2392600.0 2401700.0 2409700.0 2415200.0 2423400.0 2433800.0 2445300.0 2456200.0 2467600.0 2477500.0 2484600.0 2494800.0 2507900.0 2521800.0 2535000.0 2548200.0 2560400.0 2569400.0 2581500.0 2597100.0 2614500.0 2631400.0 2647600.0 2661500.0 2671200.0 2683900.0 2700200.0 2718700.0 2736100.0 2752000.0 2765100.0 2775200.0 2787200.0 2803600.0 2824100.0 2845300.0 2865000.0 2882300.0 2893900.0 2910100.0 2931400.0 2954000.0 2975200.0 2995200.0 3012100.0 3024600.0 3040700.0 3061500.0 3084700.0 3107300.0 3128800.0 3147100.0 3159200.0 3175600.0 3196900.0 3220300.0 3240300.0 3259000.0 3275500.0 3286400.0 3300700.0 3320300.0 3340400.0 3358000.0 3374600.0 3387800.0 3397100.0 3408800.0 3423700.0 3438800.0 3450400.0 3461700.0 3471800.0 3478600.0 3486700.0 3498400.0 3509600.0 ]; y=[infects;deads;recovered]; endfunction % Einlesen der Daten von Infizierten, Genesenen und Toten A=Daten(); inf_falleWHO=A(1,:); inf_falleWHOrecovered=A(3,:); inf_falleWHOtoten=A(2,:);
Aktuelle Impfdaten bis zum 02.06.21
function y= Impfungen()
vacc = [0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 6581.0 24741.0 42670.0 77602.0 115175.0 163424.0 163424.0 228763.0 283264.0 318674.0 366081.0 416646.0 461701.0 461701.0 532562.0 606786.0 679649.0 756333.0 834398.0 903271.0 903271.0 981914.0 1024631.0 1104504.0 1178725.0 1253306.0 1331573.0 1331573.0 1410239.0 1470822.0 1525943.0 1580628.0 1634786.0 1690351.0 1690351.0 1756478.0 1806606.0 1854928.0 1910863.0 1971043.0 2029047.0 2029047.0 2095255.0 2159412.0 2215504.0 2271784.0 2346388.0 2410230.0 2410230.0 2484408.0 2546692.0 2605818.0 2674692.0 2738103.0 2749786.0 2749786.0 2891951.0 2951692.0 3018750.0 3097094.0 3172553.0 3246005.0 3246005.0 3345235.0 3416612.0 3516986.0 3603639.0 3683054.0 3683054.0 3768080.0 3877914.0 3961165.0 4059489.0 4152414.0 4152414.0 4334170.0 4334170.0 4334170.0 4534775.0 4633859.0 4737605.0 4831522.0 4910308.0 4910308.0 5035195.0 5117056.0 5186135.0 5276028.0 5350247.0 5452990.0 5452990.0 5517282.0 5582992.0 5646788.0 5724561.0 5790531.0 5855864.0 5855864.0 5960243.0 6038063.0 6113728.0 6241152.0 6381397.0 6381397.0 6381397.0 6655866.0 6771476.0 6931584.0 7145486.0 7360108.0 7572228.0 7572228.0 7813381.0 8022890.0 8320680.0 8320680.0 8822370.0 9060934.0 9060934.0 9332160.0 9548021.0 9901626.0 10432968.0 10915832.0 11343644.0 11343644.0 11343644.0 11896572.0 12274086.0 13053626.0 13674483.0 14197101.0 14197101.0 14615052.0 15009970.0 15604092.0];
y=[vacc];
endfunction
% Einlesen der Impfungen (Zahlen entsprechen denen der vollstaendig Geimpften)
vacc=Impfungen();
% Aktuell infizierte Faelle (Gesamtfaellen an Infizierten und den Genesenen)
inf_falleWHOaktuell=inf_falleWHO-inf_falleWHOrecovered;
% Wieviele Tage Datenmaterial vorhanden
n=length(inf_falleWHO)
% Anzahl der Tage von denen Daten vorhanden sind
timesWHO=[0:1:n-1];
% Hinzufuegen von Nullen bei Impfungen, damit deren Dimensionen den Infizierten entsprechen
m=length(vacc);
vacc=[zeros(1,n-m),vacc];
mneu=length(vacc);
Plot Daten WHO
figure(1)
title ('Corona- infizierten Detuschland, Quelle RKI')
plot (timesWHO, inf_falleWHO./1000, 's', "linewidth",4, timesWHO,inf_falleWHOaktuell/1000, '*' , timesWHO,inf_falleWHOrecovered/1000,'s', timesWHO, inf_falleWHOtoten./1000 , '*' )
xlabel ('Tage von 26. Februar')
ylabel ('Zahlen in Tausend')
legend ( "German data I+R" ,"German data I","German data R", "German data deaths" ,"location", "west")
grid on
xticks([10:10:460])
axis([0,n, 0 ,450])

Berechnung der Infektionsraten auf Basis der RKI-Daten
[Bearbeiten]T=1; ccc(1)=c; for i=T+1:n ccc(i-T)=(inf_falleWHO(i)-inf_falleWHO(i-T))/(inf_falleWHO(i-T)); % NEU ---------------- % Infektionsrate aus dem beschränktem Modell ccc2(i-T)=NM*(inf_falleWHO(i)-inf_falleWHO(i-T))/(inf_falleWHO(i-T)*(NM-0.001*inf_falleWHO(i-T))); endfor
Slowdown-Funktion % val ist hier direkt die Infektionsrate! function val=slowdown2(x,t) % x=2.5 global c=0.32450; % Ab Tag t (Argument der Funktion) wird die Infektionsrate in mehreren Schritten sinken: if x<t val=0.32450 ; elseif x<t +10 val=t./(x.^1.05)*0.32450; elseif x<t +22 val=t./(x.^1.2)*0.32450; else val=t./(x.^1.27)*0.32450 ; endif %Beispielhafte Lockerung der Maßnahmen ab Tag 80, die die Infektionsrate wieder auf 50 % der Basisinfektionsrate erhöht %(um den Effekt der Lockerung zu beobachten) if x> 90 val=0.07; endif if x>150 val=0.06; endif if x>200 val=0.115; endif if x>250 val=0.15; endif if x>300 val=0.1; endif if x>330 val=0.08; endif if x>380 val=0.12; endif if x>400 val=0.195; endif if x>420 val=0.3; endif if x>440 val=0.11; endif endfunction
Einbettung slowdown-Funktion for i=1:length(timesWHO) cc(i)=slowdown2(timesWHO(i),25); % NEU: Annahme, dass Infektionsrate in einer Woche konstant ist % Gleitender Mittelwert for j=100:6:length(cc)-6 Mittelwert=sum(cc(j:j+6))/7; cc(j:j+6)=Mittelwert; endfor endfor % Resultat: Werte für unsere Infektionsrate gespeichert in dem Vektor cc
Plot der Infektionsrate und slowdown-Funktion
figure(2)
plot(timesWHO,cc)
hold on
plot (ccc, '*', ccc2 , 's')
grid on
title ('Tatsächliche und slow-down Infektionsrate')
legend ('slow-down Funktion', 'Infektionsrate c_Data')
hold off

% zum Vergleich relativer Fehler der Infektionsraten aus beschänkten und unbeschränktem Modell figure(3) plot (abs(ccc-ccc2)./ccc) %plot (NM-0.001*inf_falleWHO(2:length(timesWHO))) % Kapazität title ('Relat Fehler der unbesch. und beschr. Infektionsrate')
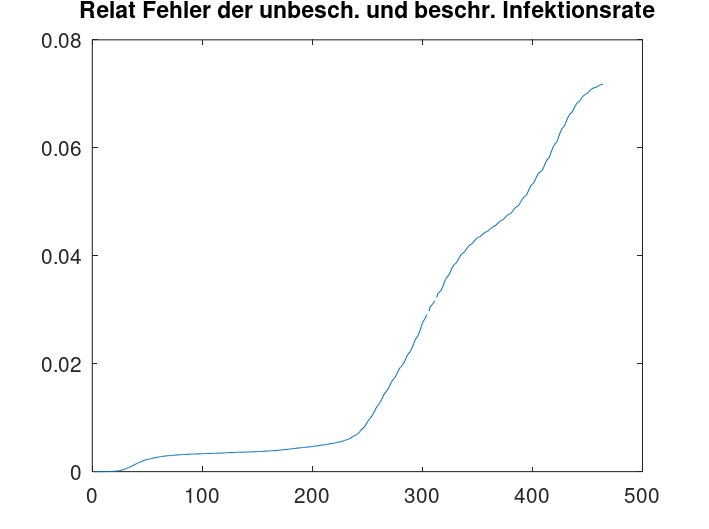
Numerische Lösung des SIR-Modells
[Bearbeiten]Weitere slowdown-Funktion
function val=slowdown(x,cc)
Rundung=floor(x);
if Rundung==0
val=cc(1,1);
else
val=cc(1,floor(x));
endif
endfunction
Lösung des ODE Systems % Times angepasst damit kein NA in relat Fehler entsteht % Beim Vergleich von Daten mit berechneten Werten, muessen die Berechnungszeiten uebereinstimmen. times=(0:0.1:465); for i=1:length(r) %Aufgabe 3 rRechnung=r(i); %Anfangsbedingungen yo=[NM-16/1000;16/1000;0]; % Loesung des Systems von gewoehnlichen Differentialgleichungen (SIR-Modell) f=@(y,x) [-slowdown(x,cc)*y(1)*y(2)/(rRechnung*NM);slowdown(x,cc)*y(1)*y(2)/NM-w*y(2);w*y(2)-0*y(2)]; y = lsode (f, yo, times); % Plot der numerischen Loesung figure(i+30) plot ( times, y (:,2), '.', times, y (:,3),'.',times, y (:,3)+y (:,2),'.') hold on plot (timesWHO, inf_falleWHO./1000, 's', "linewidth",4, timesWHO,inf_falleWHOaktuell/1000, '*' , timesWHO,inf_falleWHOrecovered/1000, '*' ) legend ( "Infected", "Removed", " Infected+Removed","German data I +R" ,"German data I ","German data R" ,"location", "west") title (["Mit r = " ,num2str(rRechnung)]); axis([0,n, 0 ,5500]) hold off
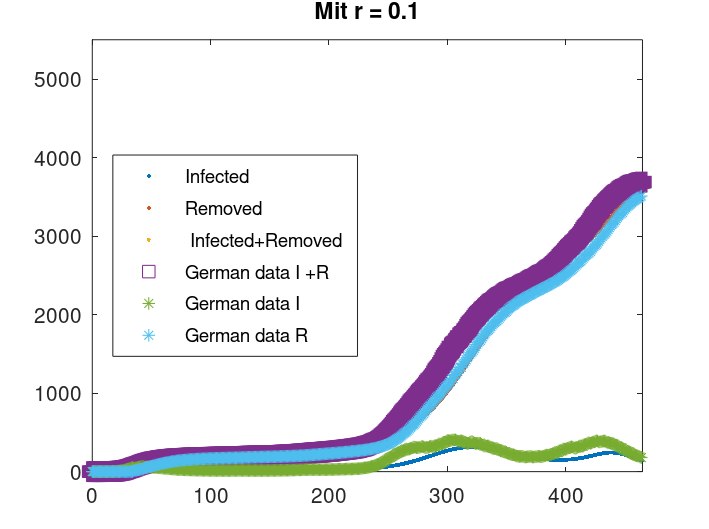
figure(i+40) plot ( times, y (:,1), '.', times, y (:,2), '.', times, y (:,3),'.',times, y (:,3)+y (:,2),'.') hold on plot (timesWHO, inf_falleWHO./1000, 's', "linewidth",4, timesWHO,inf_falleWHOaktuell/1000, '*' , timesWHO,inf_falleWHOrecovered/1000, '*' ) legend ( "Succeptible","Infected", "Removed", " Infected+Removed","German data I +R" ,"German data I ","German data R" ,"location", "west") title (["Mit r = " ,num2str(rRechnung)]); axis([0,450, 0 ,55020]) hold off endfor
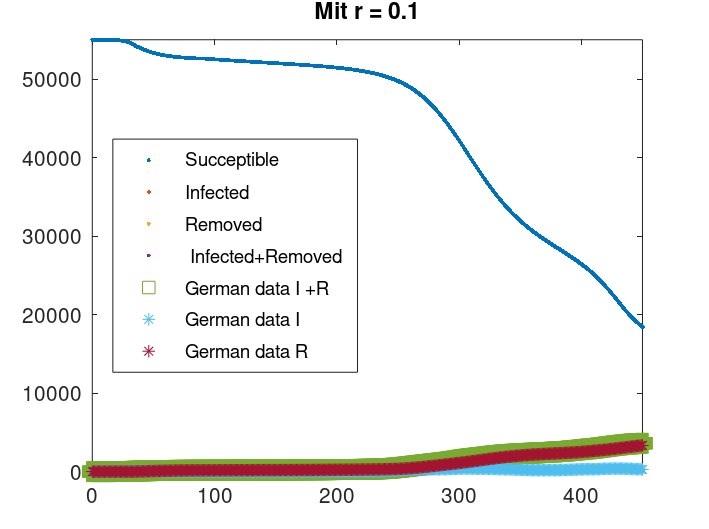
Beobachtung Aufgabe 3
Es ist deutlich zu erkennen, dass die Kurve der Infizierten (dunkelblau) ansteigt, je größer r wird. Dies bedeutet: Werden mehr Infizierte erfasst, also r größer und die Dunkelziffer damit kleiner, steigt im Umkehrschluss die Zahl der Infizierten.
Relativer Fehler der numerischen Lösung des SIR-Modells zu den RKI-Daten
[Bearbeiten]Relativer Fehler Infizierte %Interpolation der Funktionswerte an die RKI-Zeiten (Tage) I=interp1 (times, y(:,2), timesWHO+1); abs_I=abs(I-inf_falleWHOaktuell/1000); rel_I=abs(I-inf_falleWHOaktuell/1000)./(inf_falleWHOaktuell/1000);
Relativer Fehler Genesene/Toten
R=interp1 (times, y(:,3), timesWHO+1);
abs_R=abs(R-inf_falleWHOrecovered/1000);
rel_R=abs(R-inf_falleWHOrecovered/1000)./(inf_falleWHOrecovered/1000);
Plot relativer Fehler Infizierte und Genesene
figure(5)
plot (timesWHO, rel_I)
title ('relativer Fehler, Infected , Recovered')
hold on
plot (timesWHO, rel_R, '*')
hold off
legend('Infected', 'Recovered')
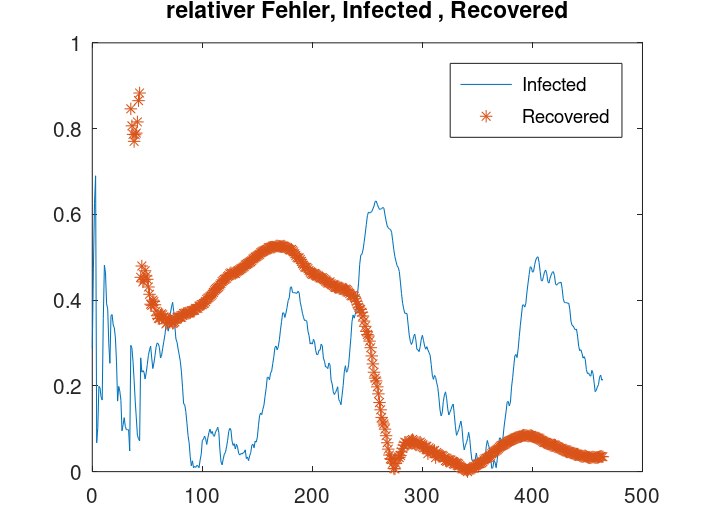
%Fehlermaß maas_I=norm(abs_I)/norm(inf_falleWHOaktuell/1000) %weiterer Fehlermaß Durchschnitt und Euklid-Norm rel_I_mean=mean(rel_I) rel_I_norm=norm(rel_I); %Fehlermaß maas_R=norm(abs_R)/norm(inf_falleWHOrecovered/1000) % weiterer Fehlermaß: Durchschnitt und Euklid-Norm rel_R_mean=mean(rel_R(36:length(timesWHO))) rel_R_norm=norm(rel_R(36:length(timesWHO)));
Impfungen
[Bearbeiten]Impffunktion %weitere slowdown-Funktion function val=Impffunktion(x) Rundung=floor(x); if x<330 val=0; elseif x<390&&x>=330 val=0.00065; elseif x<430&&x>=390 val=0.0009; elseif x<450&&x>=430 val=0.0022; else val=0.0045; endif endfunction for i=1:length(timesWHO) Impfen(i)=Impffunktion(timesWHO(i))*82000; Impfen_gesamt(i)=sum(Impfen(1:i)); endfor
Plot der Geimpften und der Impffunktion
figure(1000)
title("Impfungen auf RKI-Daten")
plot(timesWHO, vacc./1000,"s",Impfen_gesamt,"-b",Impfen)
xlabel("Tage von 26. Februar 2020")
ylabel("Zahlen in Tausend")
legend("ImpfungenRKI","Impffunktion","Tagesimpfungen")
grid on
xticks([10:20:480])
axis([0,n, 0 ,20000])
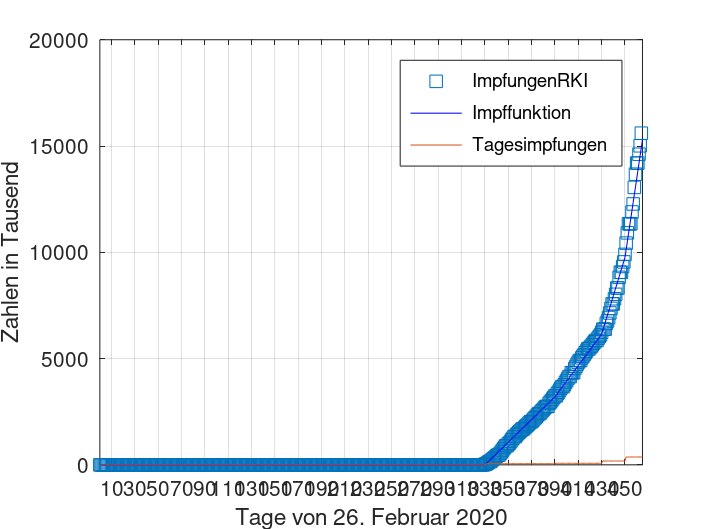
Einbauen der Impffunktion in das System %Lösung des ODE Systems % Zeitpunkt in denen numerische Loesung soll berechnet werden times=(0:0.1:460); for i=1:length(r) %Aufgabe 3 rRechnung=r(i); %Anfangsbedingungen % neue Differentialgleichung wird hinzugefuegt - SIR Modell wird um die Gruppe der Geimpften erweitert, zu Beginn: "0" Geimpfte yo=[NM-16/1000;16/1000;0;0]; % Term wurde hier hinzugefuegt - aus der Gruppe der Succeptible werden die Geimpften entfernt und in ihre eigene Gruppe hinzugefuegt f=@(y,x) [-slowdown(x,cc)*y(1)*y(2)/(rRechnung*NM)-(Impffunktion(x)*82000);slowdown(x,cc)*y(1)*y(2)/NM-w*y(2);w*y(2)-0*y(2);(Impffunktion(x)*82000)]; y = lsode (f, yo, times);
Plot ohne Succeptible
figure(i+60)
plot ( times, y (:,2), '.', times, y (:,3),'.',times, y (:,3)+y (:,2),'.',times,y(:,4),'.')
hold on
plot (timesWHO, inf_falleWHO./1000, 's', "linewidth",4, timesWHO,inf_falleWHOaktuell/1000, '*' , timesWHO,inf_falleWHOrecovered/1000, '*',timesWHO, vacc./1000,"s" )
legend ( "Infected", "Removed", " Infected+Removed","Vaccinated","German data I +R" ,"German data I ","German data R" ,"German data Vaccinated","location", "west")
title (["Mit r=" ,num2str(rRechnung)]);
axis([0,n, 0 ,5000])
hold off
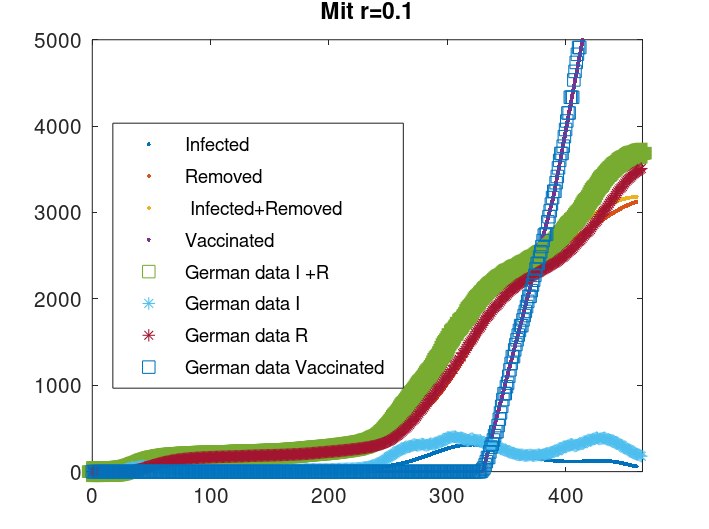
Plot mit Succeptible
figure(i+70)
plot ( times, y (:,1),times, y (:,2), '.', times, y (:,3),'.',times, y (:,3)+y (:,2),'.',times,y(:,4),'.')
hold on
plot (timesWHO, inf_falleWHO./1000, 's', "linewidth",4, timesWHO,inf_falleWHOaktuell/1000, '*' , timesWHO,inf_falleWHOrecovered/1000, '*',timesWHO, vacc./1000,"s" )
legend ("Succeptible","Infected", "Removed", " Infected+Removed","Vaccinated","German data I +R" ,"German data I ","German data R", "German data Vaccinated","location", "west")
title (["Mit r = " ,num2str(rRechnung)]);
axis([0,450, 0 ,55020])
hold off

close(i+70) endfor
Tutorium 4
[Bearbeiten]Aufgabenteil a)
[Bearbeiten]Implementierung der Randwertaufgabe für Dirichlet-Randbedingungen
[Bearbeiten] % Quellfunktion f der rechten Seite der Poissongleichung wird definiert:
function wert=Quellfunktion(x,y)
if sqrt((x.-3.25).^2+(y.-3).^2)<=0.35 wert=1;
else wert=0;
endif
endfunction
% Erstellung eines aequidistanten Gitters
% Gebiet D wird definiert:
xend=8;
yend=5.0;
N=50 % Anzahl der Punkte
hx=xend/(N+1) % Schrittweite ergibt sich aus der Laenge von x und der Anzahl der Punkte hy=hx; % aequidistantes Gitter M=floor((yend/hy))-1 % Koordinatenmatrix der Gitterpunkte [x,y]=meshgrid(hx:hx:xend-hx,hy:hy:yend-hy);
a=1.0; % konstanter Diffusionskoeffizient
% Dirichlet Randwertbedingung: % Bei der Wahl von "0" handelt es sich um ein homogenes Dirichlet Randwertproblem wert_unten= 0.3; wert_oben=0.32; wert_links=0.3; wert_rechts=0.15;
% Definition der Systemmatrix
% Definition des ersten Blocks - Tridiagonale Matrix Block=zeros(N,N); Block1=Block-4.*eye(N,N); % eye Einheitsmatrix Block1=Block1.+diag(ones(N-1,1),1); % fuegt Einsen auf der oberen, ersten Nebendiagonalen ein Block1=Block1.+diag(ones(N-1,1),-1);% fuegt Einsen auf der unteren, ersten Nebendiagonalen ein
% N x N Einheitsmatrix
Block2=eye(N,N);
Ah=zeros(N*M);
for i=1:M % Blockhauptdiagonale (B's) Ah(N*(i-1)+1:N*i,N*(i-1)+1:N*i)=Block1; % (1:50,1:50) (x-Richtung, y-Richtung) % 51:100 % 101:150 endfor
% Einsortierung der Einheitsmatritzen (Block2) for j=2:M % Obere Blocknebendiagonale (I's) % (1:50,51:100) (51:100,101:150) Ah(N*(j-2)+1:N*(j-1),N*(j-1)+1:N*j)=Block2; % Untere Blocknebendiagonale (I's) % (51:100,1:50) (101:150,51:100) Ah(N*(j-1)+1:N*j,N*(j-2)+1:N*(j-1))=Block2; endfor
% Plotten
figure(1)
spy(Ah)
xlabel("Spalten")
ylabel("Zeilen")
title("Systemmatrix Ah")
% Matrix mit Diffkoeff/h^2 multiplizieren
Ah=Ah*a/hx^2;

% rechte Seite des Systems clear f; for i=1:N for j=1:M % Berechnung der "f's" der Quellfunktion auf der rechten Seite f(j,i)=1*Quellfunktion(x(j,i),y(j,i));
% Dirichlet Randbedingung unten: if j==1 f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+ wert_unten*(a/hx^2);endif % Dirichlet Randbedingung oben: if j==M f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+wert_oben*(a/hx^2);endif
% Dirichlet Randbedingung links: if (i==1)% ||(i==N ) % mathematische "Oder" in Octave f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+wert_links*(a/hx^2);endif % Dirichlet Randbedingung rechts: if (i==N) f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+wert_rechts*(a/hx^2);endif endfor endfor
% Werte der Ecken:
f(1,1)=1*Quellfunktion(x(1,1),y(1,1))+ (wert_links+wert_unten)*(a/hx^2);
f(1,N)= 1*Quellfunktion(x(1,N),y(1,N))+ (wert_rechts+wert_unten)*(a/hx^2);
f(M,1)=1*Quellfunktion(x(M,1),y(M,1))+ (wert_links+wert_oben)*(a/hx^2);
f(M,N)=1*Quellfunktion(x(M,N),y(M,N))+ (wert_rechts+wert_oben)*(a/hx^2);
size (f)
% reshape funktioniert Spaltenmässig: es wird Spalte1, dann Spalte2,... eingeordnet, wobei wir die Matrix f nach Reihen/Zeilen einordnen.
% Daher soll die Matrix f' mit N(Zeilen)x M(Spalten) in ein langern Vektor eingeordnet.
b=-1*reshape(f',N*M,1);
% Loesungschritt
sol=Ah\b;
sol_matrix=reshape(sol,N,M);% Matrix mit N(Zeilen)x M(Spalten) sol_matrix=sol_matrix'; % Transponiert, wegen reshape
% Oeffne ein Bildfenster und plotte die Lösung auf dem realen Koordinatenfeld
figure(2);
surfc(x,y,sol_matrix);
title ("Loesung");
ylabel("y")
xlabel("x")
colormap("hsv")
colorbar

% weiteres Bild mit Quellfunktion- rechte Seite des Systems figure(3); surfc(x,y,f); title ("Quellfunktion"); ylabel("y") xlabel("x") % colormap("hsv")

Aufgabenteil b)
[Bearbeiten]clear all;
function wert=Quellfunktion(x,y)
if sqrt((x.-3.25).^2+(y.-3).^2)<=0.35 wert=1;
else wert=0;
endif
endfunction
% definiere Gebiet D xend=8; yend=5.0; N=80 % Anzahl der Punkte
hx=xend/(N+1)
hy=hx;
M=floor((yend/hy))-1
% Koordinatenmatrix der Gitterpunkte
[x,y]=meshgrid(0:hx:xend,0:hy:yend);
a=1.0; % konstanter Diffusionskoeffizient
% Randbedingungen(=0)
wert_links=0;
% Definition der Systemmatrix % Bei Neumann ist die Systemmatrix von der Groesse (N+2)*(M+2)x(N+2)*(M+2) N=N+2; M=M+2; Ah=zeros(N*M);
% Definition des ersten Blocks - Tridiagonale Matrix Block=zeros(N,N); Block1=Block-4.*eye(N,N); Block1=Block1.+diag(ones(N-1,1),1); % fuegt Einsen auf der oberen, ersten Nebendiagonalen ein Block1=Block1.+diag(ones(N-1,1),-1);% fuegt Einsen auf der unteren, ersten Nebendiagonalen ein
Block3=eye(N,N)*hx;
% Definition Neumann Randbedingungen unten
Ah(1:N,1:N)=Block3;
Ah(1:N,N+1:2*N)=-Block3;
% Definition Neumann Randbedingungen oben
Ah(N*M-(N-2)-1:N*M,N*M-(N-2)-1:N*M)=Block3;
Ah(N*M-(N-2)-1:N*M,N*M-N-(N-2)-1:N*M-N)=-Block3;
% N x N Einheitsmatrix
Block2=eye(N,N);
Block2(1,1)=0;
Block2(N,N)=0;
for i=2:M-1 Ah(N*(i-1)+1:N*i,N*(i-1)+1:N*i)=Block1; %(1:50,1:50) (x-Richtung, y-Richtung) % 51:100 % 101:150 endfor
% Einsortierung der Einheitsmatritzen (Block2) % obere Nebendiagonale for j=3:M % (1:50,51:100) (51:100,101:150) Ah(N*(j-2)+1:N*(j-1),N*(j-1)+1:N*j)=Block2; endfor
% untere Nebendiagonale for j=2:M-1 % (51:100,1:50) (101:150,51:100) Ah(N*(j-1)+1:N*j,N*(j-2)+1:N*(j-1))=Block2; endfor
figure(1)
spy(Ah)
xlabel("Spalten")
ylabel("Zeilen")
title("Systemmatrix Ah")

% Matrix mit Diffkoeff/h^2 multiplizieren
Ah1=Ah*a/hx.^2;
% rechte Seite des Systems
clear f;
for i=1:N
for j=1:M
f(j,i)=1*Quellfunktion(x(j,i),y(j,i));
% Dirichlet Randbedingung links: if (i==1)||(i==N ) % mathematische "Oder" in Octave f(j,i)=1*Quellfunktion(x(j,i),y(j,i))+wert_links*(a/(hx.^2)); endif endfor endfor
% Werte der Ecken % Damit sich in den Ecken Neumann realisiert, werden hier die Dirichlet Randbedingungen Null gesetzt f(1,1)=1*Quellfunktion(x(1,1),y(1,1))+ 0; f(1,N)= 1*Quellfunktion(x(1,N),y(1,N))+ 0; f(M,1)=1*Quellfunktion(x(M,1),y(M,1))+ 0 ; f(M,N)=1*Quellfunktion(x(M,N),y(M,N))+ 0;
size (f)
b=-1*reshape(f',N*M,1); % Spalten
% Loesungsschritt
sol=Ah1\b;
sol_matrix=reshape(sol,N,M);% Matrix mit N(Zeilen)x M(Spalten) sol_matrix=sol_matrix'; % Transponiert, wegen reshape
% Oeffne ein Bildfenster und plotte die Lösung auf dem realen Koordinatenfeld
figure(2);
surfc(x,y,sol_matrix);
title ("Loesung");
ylabel("y")
xlabel("x")
colormap("hsv")
colorbar

% weiteres Bild mit Quellfunktion- rechte Seite des Systems figure(3); surfc(x,y,f); title ("Quellfunktion"); ylabel("y") xlabel("x") % colormap("hsv")

Tutorium 5
[Bearbeiten]clear all close all
% Allgemeine Parameter --------------------------------------------------------- a=0.1; %(konstanter Diffusionskoeffizient) Tage=200 %(Zeitintervall in Tagen) delta_t=0.1 %(Zeitschritt) Zeitschritte=floor(Tage/delta_t) %Für Reaktionsdiffusionsgleichung: Infektionsrate=0.3 %(Infektionsrate, Vorsicht k=c/B in unserem Modell k.u.(B-u)-w.u) Wechselrate=1/14 %Wechselrate Speicherung=true; mitImpfungen=true; Impfrate_Beginn=0;
% Einlesen der Bevoelkerungsdichte ---------------------------------------------
A=imread ('Monitor_Einwohnerzahl_detail.png');
%Ausschnitt aus dem Bild der Groesse 15x18 Picksel
% hier kein Ausschnitt gewaehlt
S=A;
Groesse_Matrix=size(A)
% Bildebenen S1=A(:,:,1); S2=A(:,:,2); S3=A(:,:,3); % man sieht, S ist hier nur eine 2D Matrix size(S1) %___ [s1 s2 s3]=size(S) S1=double (S1); S2=double (S2); S3=double (S3); A=S1+S2+S3; %___ S1=S1./A; S2=S2./A; S3=S3./A; % Farbebene rot minus grau, geht von ca 20-100% S=S1.-0.4.*(S2.+S3)/1.4; % Alternativ (Gesamtintensitaet in umgedrehter Skala, max ist 255) maxA=max(max(A)) %S=abs(A/maxA-1.1); % nicht von uns bevorzugt % oder nur die Skala der roten Farbtonen, heruntergesetzt, da diese bei 40 % anfaengt S=S1-0.29;
%Konstante maximale Bevölkerungsdichte und weitere Definitionen
%----------------------------------------------------
B=3;% in Tausend: 800 Einwohner pro km^2 Konstante Bevölkerungsdichte pro km^2
% das physische räumliche Gebiet an die räumliche Koordinaten des Bildes, oder dessen Ausschnittes anpassen
yend=s1;
xend=s2;
N=s2%hier ist eine Rasterzelle des FDM Verfahren genau gleich dem Pixel des eingelesenen Bildes
% alternativ
N=2*s2
%hier ist die Laenge einer Rasterzelle des FDM Verfahren 3-fach kleiner als die Länge des Pixel des eingelesenen Bildes
%___
%Zeitschritte=10
hx=xend/(N+1)
hy=hx;
M=floor((yend/hy))-1
[x,y]=meshgrid(0:hx:xend,0:hy:yend);
N=N+2;
M=M+2;
%___
%Bilddarstellung
%----------------------------------------------------
figure(Zeitschritte+1000);
surface(S)
title ("Bevoelkerungsdichte eingelesen, nicht flipped ");
colorbar
%___
Max=max(max(S));
%%%%S=abs(S-Max); manchmal hat helle Farbe niedrigeren Wert
%Interpolieren an die Koordinatenmatrix (0,xend) x (0 yend) der numerischen Berechnung
%-----------------
Sint=interp2(S,xend*(1*x.+2)/(xend+2),yend*(1*y.+2)/(yend+2), 'cubic');
%%% AH hier funktioniert dies nur im Falle eines Bildes aus einer Ebene
%Sint=interp2(S,x,y, 'cubic');
ss=size (Sint)
%___
%Korrektur -keine Null Bevölkerungsdichte
% und up-down flippen, da y-Koordinate im Image von oben nach unten lä, bei uns von unten nach oben,
% daher Bild flippen, oben <-> unten
%-----------------
% keine künstliche Verschiebung nun notwendig
Sint=flipud (Sint).+0.0*Max;
%___
figure(Zeitschritte+1001);
surface(x,y, 1000*(B/Max)*Sint*hx^2,"EdgeColor", "none")
title (["Bevoelkerungszahl (pro Pixel) h^2=",num2str(hx^2)] );
ylabel("y (km)")
xlabel("x (km) ")
colorbar
colormap ocean %autumn, hsv jet ocean
axis([0 xend 0 yend -0.005 1100*max(max(B))])
%___
%Optional: Speicherung der Bilder
%test=["B_Anzahl.jpg"];
%saveas(Zeitschritte+2,test)
%Integral der Bevölkerungsdichte: Gesamtbevoelkerung in unserem Gebiet und Duchschnittsbevölkerung %Bev=integrate(0:hx:xend,integrate (0:hy:yend, Sint*B)) Bev=sum(sum(Sint*B))*hx^2 Bev_duchschnitt=sum(sum(Sint*B))*hx^2/(xend*yend) %___ %WICHTIG %Bevoelkerungsdiche als ein langer Vektor abspeichern (fuer die Update Berechnung in Euler Zetschritt) B=reshape((B/Max)*Sint',N*M,1); %size (B);
% Definition der Systemmatrix % Bei Neumann ist die Systemmatrix von der Groesse (N+2)*(M+2)x(N+2)*(M+2) %___ %N=N+2; %oben schon definiert %M=M+2; Ah=zeros(N*M); % % Definition des ersten Blocks - Tridiagonale Matrix Block=zeros(N,N); Block1=Block-4.*eye(N,N); Block1=Block1.+diag(ones(N-1,1),1); %fuegt Einsen auf der oberen, ersten Nebendiagonalen ein Block1=Block1.+diag(ones(N-1,1),-1); % fuegt Einsen auf der unteren, ersten Nebendiagonalen ein %___ % N x N Einheitsmatrix Block2=eye(N,N); %___ % NEUMANN ----------------------------------------------------------------------- % Definiert fuer den linken Rand %___ Block1(1,1)=hx; Block1(1,2)=-hx; %___ % Definiert fuer den rechten Rand Block1(N,N)=hx; Block1(N,N-1)=-hx; %___ Block2(1,1)=0; Block2(N,N)=0; %___ Block3=eye(N,N)*hx; %___ % Einsortierung der neuen Bloecke fuer Neumann unten und oben % Definition Neumann Randbedingungen unten Ah(1:N,1:N)=Block3; Ah(1:N,N+1:2*N)=-Block3; %___ % Definition Neumann Randbedingungen oben Ah(N*M-(N-2)-1:N*M,N*M-(N-2)-1:N*M)=Block3; Ah(N*M-(N-2)-1:N*M,N*M-N-(N-2)-1:N*M-N)=-Block3; %------------------------------------------------------------------------------- %___ % Einsortierung der tridiagonalen Matrix for i=2:M-1 Ah(N*(i-1)+1:N*i,N*(i-1)+1:N*i)=Block1; %(1:50,1:50) (x-Richtung, y-Richtung) %51:100 %101:150 endfor %___ % Einsortierung der Einheitsmatritzen (Block2) % obere Nebendiagonale for j=3:M % (1:50,51:100) (51:100,101:150) Ah(N*(j-2)+1:N*(j-1),N*(j-1)+1:N*j)=Block2; endfor
% untere Nebendiagonale
for j=2:M-1
% (51:100,1:50) (101:150,51:100)
Ah(N*(j-1)+1:N*j,N*(j-2)+1:N*(j-1))=Block2;
endfor
%___
%-------------------------------------------
% Matrix mit Diffkoeff/h^2 multiplizieren
%-------------------------------------------
Ah1=Ah*a/hx.^2;
%___
%Matrixdarstellung - optional
figure (1004);
spy (Ah1);
xlabel("Spalten")
ylabel("Zeilen")
zlabel("Matrix B")
title ("Systematrix Ah");
% gekoppelte Reaktionsdiffusionsgleichung - Reaktionsterme
function F=F_I (c,w,B,ui,us)
F=(c./B).*ui.*us-w*ui;
endfunction
%___
function F=F_S (c,B,ui,us)
F=-1*(c./B).*ui.*us;
endfunction
%___
% Reaktiuonsterm mit Berücksichtigung der Impfungen
% aus der Gruppe der Succeptible wird in jedem Zeitschritt ein bestimmter Prozentsatz
% der Bevoelkerung entfernt
function F=F_S_Impf (c,B,ui,us,Impfrate)
F=-1*(c./B).*ui.*us-Impfrate*B;
endfunction
%___
%Anfangslösung als Matrix
% Tag 0
N1=N-2;
M1=M-2;
%___
for i=1:N
for j=1:M
%___
% Genauer Anschauen wieviel Infizierte wollen wir haben
initial(j,i)=0.001*initialfunction(x(j,i),y(j,i));
%0.005 und 0.01 (in Tausend) d.h. 5 und 10 pro gegebene Fläche pi*R^2
endfor
endfor
Anfangsinfizierte=1000*sum(sum(initial))*hx^2
%___
B=reshape(B',N*M,1);
size (initial)
size(B)
u_i_alt=1*reshape(initial',N*M,1); % Infizierte zum Zeitpunkt "0"
u_s_alt=B.-u_i_alt; % Bevoelkerung ohne die Infizierten
%reshape funktioniert Spaltenmässig: Sp1,Sp2, wir wollen Zeilenmässig
%Matrix f' ist N(Zeilen)x M(Spalten)
figure(1005)
surface(x,y,initial);
title ("Anfangsloesung");
ylabel("y")
xlabel("x")
%___
if mitImpfungen==true
% Die Anzahl der Succeptible, wenn zu Beginn schon ein gewisser Prozentsatz geimpft ist
% Festgelegt durch Prozentsatz von der Gesamtbevoelkerung
u_s_alt=u_s_alt-Impfrate_Beginn*B;
endif
for t=1:Zeitschritte
%Impfungen
if mitImpfungen==true
% Festlegung der Impfrate zu Beginn des Tages
if mod(t,1/delta_t)==0 || t==1
% Impfungsrate am entsprechenden Tag herausbekommen - beginnend mit dem Starttag
Impfindex=t*delta_t;
% Impfrate pro Tag - wird anschließend gleichverteilt über den Tag angenommen
ImpfungenProzent=Impffunktion(Impfindex);
% SpeicherImpfungen(:,t)=ImpfungenProzent;
endif
endif
Erkrankungsrate=slowdown(t*delta_t,25)*Infektionsrate;
% Berechnung der einzelnen Zeischritte durch das explizite Eulerverfahren
u_i=u_i_alt + delta_t * (1*Ah1 *u_i_alt +1*F_I(Erkrankungsrate,Wechselrate,B,u_i_alt,u_s_alt));
if mitImpfungen==true
u_s=u_s_alt + delta_t * (1*Ah1 *u_s_alt +1*F_S_Impf(Erkrankungsrate,B,u_i_alt,u_s_alt,ImpfungenProzent));
else
u_s=u_s_alt + delta_t * (1*Ah1 *u_s_alt +1*F_S(Erkrankungsrate,B,u_i_alt,u_s_alt));
endif
u_i_alt=u_i; u_s_alt=u_s; %Reaktionsterme fuer aktuell Infizierte und Anfaellige %AH dies muss man nich speichern %SpeicherungErkrankungsrate(1,t)=Erkrankungsrate; SpeicherUI(:,t)=u_i; SpeicherUS(:,t)=u_s;
endfor
fig_index=1:1:Zeitschritte;
Plot=101;
%___
for i=fig_index
%___
% Aus langem Vektor SpeicherUI wird die entsprechende Spalte herausgelesen
% Anpassung an das Gitter
Loesung=reshape(SpeicherUI(:,i),N,M);% Matrix mit N(Zeilen)x M(Spalten)
Loesung=Loesung';
%___
if mod(i,1/delta_t)==0
figure(delta_t*i)
surfc(x,y,Loesung, "EdgeColor", "none")
%%% view(0,90)
%___
% Verschiedene Farbpalleten
% colormap: autumn, hsv jet ocean
colormap ("jet")
colorbar
%___
% Berechnung der Gesamtinfizierten zum Zeitpunkt des Plots
InfizierteGesamt=floor(sum(sum(Loesung))*hx^2*1000);
%___
% Skala wird an die Bevölkerungsdichte angepasst
axis([0 xend 0 yend -0.001 1*max(max(B))])
%___
title (["Loesung in t=", num2str(delta_t*i), " Infizierte=" num2str(InfizierteGesamt)]);
ylabel("y")
xlabel("x")
caxis([0 0.1])
view(2)
if Speicherung==true
% Optional: Speicherung der Bilder
test=["Images/Fig_", num2str(delta_t*i),".jpg"]
saveas(delta_t*i, test)
endif
endif
Plot=Plot+1;
endfor
%-------------------------------------------------
%___
%weiteres Bild mit Anfangsfunktion
%figure(Zeitschritte+1);
%surface(x,y,initial);
%title ("Anfangsloesung");
%ylabel("y")
%xlabel("x")
Animationen 500 Tage ohne Impfungen
500 Tage zu Beginn 20% geimpft
500 Tage zu Beginn 60% geimpft
Ergänzungen Octave-Tutorial
[Bearbeiten]Diese Ergänzungen wurden bei dem Octave-Tutorial vorgenommen, um die Implementation der Gruppe bzgl. der verwendeten Octave-Befehle nachvollziehbar zu machen.
- Matrix-Multiplikation in Octave - notwendig für die Modellierung diskreter Transportprozesse.
Skripte in Octave
[Bearbeiten]Referenzieren Sie hier die von Ihnen verwendeten Skripte und Bibliotheken in Octave oder R/Studio
Literatur
[Bearbeiten]Notieren Sie hier die von Ihnen verwendete Literatur
- Quelle 1





