Gruppenseite - GLP

Diese Seite enthält die gesammelten Materialien der Gruppe 2 - GLP für die Portfolioprüfung.

COVID-19/Mathematische Modellbildung

Teilnehmer-innen

Gauer, Birgit
Lemke, Christina
Pfaffmann, Christoph

Relevanz der Thematik

Im Rahmen des Moduls haben wir uns mit der Modellierung der Verbreitung des Corona-Virus befasst. Die Relevanz der Thematik spiegelt sich in den UN-Zielen für nachhaltige Entwicklung wider.

Ziel 3 (Gesundheit und Wohlergehen): Ein wichtiges Ziel der Vereinten Nationen ist es, für alle Menschen gleichermaßen ein gesundes Leben zu gewährleisten und ihr Wohlergehen zu fördern. Im Zuge der Corona-Pandemie bedeutet das eine bestmögliche (den Umständen entsprechend notwendige) medizinische Versorgung für alle Infizierte. Dies gelingt nur, wenn die Kapazitäten der Gesundheitssysteme nicht überlastet sind. Mit einer Überforderung der Gesundheitssysteme geht eine höhere Mortalität einher.
Ziel 17 (Partnerschaften zur Erreichung der Ziele): Um Ziel 3 zu verwirklichen, ist eine Zusammenarbeit der verschiedenen Nationen sinnvoll. Dies betrifft nicht nur präventive Maßnahmen (z.B. Bewegungseinschränkungen) sondern auch akute. Ein Beispiel: Inifzierte aus Frankreich (v.a. Intensivpatienten) wurden nach Deutschland gebracht und in deutschen Krankenhäusern behandelt, da die Kapazitäten der französischen Bezirke ausgereizt waren. Nur durch diese Kooperation war eine adäquate medizinische Versorgung möglich.

Zur Erfüllung von Ziel 3 wurden von Seiten der Politik Maßnahmen ergriffen, die zur Eindämmung der Virusverbreitung beigetragen haben (z.B. Kontaktverbot). Ziel dieser Maßnahmen war, die Infektionsverbreitung über einen längeren Zeitraum zu strecken ("flatten the curve"), um das Gesundheitssystem nicht zu überlasten. Diese Maßnahmen stellten jedoch Gradwanderungem dar, da auf der anderen Seite wirtschaftliche Betriebe starke finanzielle Rückschläge erlitten und bis heute um ihre Existenz kämpfen.
Betroffen sind davon u.a. Veranstaltungsgewerbe (Verbot von Großveranstaltungen, auch kleinere Veranstaltungen), Reisegewerbe (Hotels, Reisebüros, Fluggesellschaften), Restaurants, Friseure, Bekleidungsgeschäfte (1. schwierige Umsetzung der Hygieneregeln, 2. Leute geben weniger Geld aus, da sie nur noch Kurzarbeitergeld erhalten) und jegliche Unternehmen mit Angebot von Freizeitaktivitäten (Schwimmbäder, Clubs, Freizeitparks etc.).
Finanzielle Engpässe entstanden nicht nur auf Seiten der Firmenleitung; auch Angestellte spürten diese Krise, da z.B. unerwartet Kurzarbeitergeld statt des gewohnten Gehalts ausgezahlt wurde. Das Erreichen von Ziel 3 ist in diesem Fall scheinbar kaum umsetzbar unter Berücksichtigung von Ziel 8 (Menschenwürdige Arbeit und Wirtschaftwachstum). Finanzielle Unterstützungen von der Regierung sollten in dieser Krise einen Teil der finanziellen Einbußen auffangen. Diese Zahlungen können einen Bankrott dennoch zum Teil nicht verhindern: 1. Diese verhältnismäßig kleinen Summen (im Vergleich zum eigentlichen Umsatz der Unternehmen) kompensieren die extrem hohen Verliste nicht. 2. Bis zum Zeitpunkt der tatsächlichen Auszahlung sind einige Betriebe schon vorher gewzungen, ihren Betrieb zu schließen.

Modelle

In unseren beiden Modellen werden Auswirkungen unterschiedlicher Bewegungsmuster auf die Verbreitung des Corona-Virus untersucht.
Grundlage bildet das SIR-Modell.

Die folgenden Modelle wurden implementiert.

Modell 1: SIR-Model mit Austauschmatrix

In Modell 1 implementieren wir das SIR-Modell in Octave unter Berücksichtigung erster Bewegungsmuster.
Wir betrachten im Folgenden 5 Gebiete mit gleicher Einwohnerzahl. Es finden Bewegungen zwischen den Gebieten statt bis zu einem bestimmten Tag ("Lockdown").

Implementation grundlegender Parameter

Im ersten Schritt implementieren wir grundlegende Parameter.

%Plotten ein/ausschalten 
plotteInMehrereGrafiken = true;
plotsAlsBilderSpeichern = false;

erkrankungsrate = [0.25, 0.25, 0.25, 0.25, 0.25];    %in allen 5 Gebieten ist die Erkrankungsrate gleich 
genesungsrate = 1/14;
Gebiete=5;                %Anzahl der Gebiete 
einwohnerzahl= 1000;      %Einwohnerzahl in einem Gebiet 
t=150;                    %Anzahl der Zeitschritte t: hier entspricht 1 Zeitschritt 1 Tag

Die Erkrankungsrate setzt sich zusammen aus dem Produkt der Wahrscheinlichkeit einer Infektionsübertragung bei Kontakt und der Kontaktrate (mit wie vielen Personen tritt ein Infizierter pro Tag in Kontakt). Diese Rate ist hier ein geschätzter Wert. Die Genesungsrate beschreibt die lineare Rate, mit der ein Infizierter wieder gesund wird. Diese wird auf 1/14 geschätzt aufgrund der Annahme, dass nach 14 Tagen ein Infizierter vollständig genesen ist.

Initialisierung für die Vektoren von S,I,R

Im nächsten Schritt werden S, I und R implementiert. Zunächst befindet sich nur in Gebiet 1 ein Infizierter. Erst durch die Austauschbewegungen verbreitet sich das Virus in die anderen Gebieten.

S, I, R sind Matrizen, die Spaltenanzahl entspricht jeweils der Gebietsanzahl. Die Reihenanzahl entspricht der Anazhl von Tag 0 bis zum letzten berechneten Tag ( $T+1$ -Tage).

${\textstyle T\in \mathbb {N} }$ , Anzahl Tage
${\textstyle t_{i},\,i\in \{0,1,\dots ,T\}}$ , Zeitschritte
$G\in \mathbb {N}$ , Anzahl Gebiete
${\textstyle g_{j},\,j\in \{1,\dots ,G\}}$ ,Gebiete

S:=Mat({(T+1)}\times G,\mathbb {R} ),\,I:=Mat({(T+1)}\times G,\mathbb {R} ),\,R:=Mat({(T+1)}\times G,\mathbb {R} )

S={\begin{pmatrix}s_{t_{0},g_{1}}&s_{t_{0},g_{2}}&\dots &s_{t_{0},g_{G}}\\s_{t_{1},g_{1}}&s_{t_{1},g_{2}}&\dots &s_{t_{1},g_{G}}\\\vdots &\vdots &\ddots &\vdots \\s_{t_{T},g_{1}}&s_{t_{T},g_{2}}&\dots &s_{t_{T},g_{G}}\\\end{pmatrix}},\,I={\begin{pmatrix}i_{t_{0},g_{1}}&i_{t_{0},g_{2}}&\dots &i_{t_{0},g_{G}}\\i_{t_{1},g_{1}}&i_{t_{1},g_{2}}&\dots &i_{t_{1},g_{G}}\\\vdots &\vdots &\ddots &\vdots \\i_{t_{T},g_{1}}&i_{t_{T},g_{2}}&\dots &i_{t_{T},g_{G}}\\\end{pmatrix}},\,R={\begin{pmatrix}r_{t_{0},g_{1}}&r_{t_{0},g_{2}}&\dots &r_{t_{0},g_{G}}\\r_{t_{1},g_{1}}&r_{t_{1},g_{2}}&\dots &r_{t_{1},g_{G}}\\\vdots &\vdots &\ddots &\vdots \\r_{t_{T},g_{1}}&r_{t_{T},g_{2}}&\dots &r_{t_{T},g_{G}}\\\end{pmatrix}}

$s_{t_{i},g_{j}}\in \mathbb {R}$ , Anzahl Susceptibles in Zeitschritt $t_{i}$ und Gebiet $g_{j}$
$i_{t_{i},g_{j}}\in \mathbb {R}$ , Anzahl Infected in Zeitschritt $t_{i}$ und Gebiet $g_{j}$
$r_{t_{i},g_{j}}\in \mathbb {R}$ , Anzahl Recovered in Zeitschritt $t_{i}$ und Gebiet $g_{j}$

%Anfangsmatrizen festlegen 
S=zeros(t+1,Gebiete);
I=zeros(t+1,Gebiete);
R=zeros(t+1,Gebiete);

S\_startwert:=Mat({1}\times G,\mathbb {R} ),\,I\_startwert:=Mat({1}\times G,\mathbb {R} ),\,R\_startwert:=Mat({1}\times G,\mathbb {R} )

%Startwerte für die einzelnen Gebiete festlegen 
I_start = 1/einwohnerzahl; 
S_startwert = [1-I_start,1,1,1,1];
I_startwert=[I_start,0,0,0,0]; 
R_startwert=[0,0,0,0,0];

%Anfangsmatrizen überschreiben 
S(1,:)= S_startwert;        %alle Spalteneinträge von S_startwert werden in die Spalten der ersten Zeile von S eingetragen 
I(1,:)= I_startwert;
R(1,:)= R_startwert

Festlegung von Austauschmatrizen

Es können verschiedene Austauschmatrizen festgelegt werden. Mit der Variablen matrix = kann ausgewählt werden, welche Austauschmatrix in einem Durchlauf verwendet werden soll.

Austauschmatrix:=Mat({G}\times G,[0,1]\subset \mathbb {R} )

%------------------------------------------------------------------------------- 
%Programmiere Bewegungsmuster 
%------------------------------------------------------------------------------- 
matrix = 1;
if (matrix == 1)
Austauschmatrix = [0.9 , 0.02 , 0.01 , 0.05 , 0.02;
                   0.03, 0.91 , 0.02 , 0.02 , 0.02;
                   0.02, 0.04 , 0.88 , 0.03 , 0.03;
                   0.05, 0.02 , 0.01 , 0.89 , 0.03;
                   0   , 0.01 , 0.08 , 0.01,  0.9  ];
%------------------------------------------------------------------------------- 
endif

Festlegung eines Lockdowns

Nun kann die Implementierung von S, I und R unter Berücksichtigung der Austauschbewegungen fortgeführt und geplottet werden.
Zudem wird festgelegt, dass ab einem bestimmten Tag $t_{i}$ die Bewegungen eingeschränkt werden. Es wird quasi ein "Lockdown" festgelegt, ab dem keinerlei Bewegungen mehr zwischen den Gebieten möglich ist.

S'(t)=-kI(t)S(t),

I'(t)=kI(t)S(t)-wI(t),

R'(t)=wI(t),

wobei die Rate $w=1/T_{inf}$ sich als Umkehrwert der Genesungszeit $T_{inf}$ (infektiöser Periode, hier 14 Tage) berechnet. $k$ ist die Erkrankungsrate.
Setzt man für die obigen Gleichungen die Definition des Differenzenquotienten ein, ergibt sich:

S'(t_{i})=\displaystyle \lim _{h\to 0}{\frac {S(t_{i}+h)-S(t_{i})}{h}}=-kI(t_{i})S(t_{i}),

I'(t_{i})=\displaystyle \lim _{h\to 0}{\frac {I(t_{i}+h)-I(t_{i})}{h}}=kI(t_{i})S(t_{i})-wI(t_{i}),

R'(t_{i})=\displaystyle \lim _{h\to 0}{\frac {R(t_{i}+h)-R(t_{i})}{h}}=wI(t_{i}),

mit $h=1$ erhält man die, auch in Octave so umgesetzte, Näherung. Da $h$ als ein ganzer Tag angenommen wird, kann man $h$ in den Index von $t$ schreiben.

{\begin{array}{rcl}\displaystyle {\frac {S(t_{i+1})-S(t_{i})}{1}}=-kI(t_{i})S(t_{i})&\Leftrightarrow &S(t_{i+1})=S(t_{i})-kI(t_{i})S(t_{i})\\\displaystyle {\frac {I(t_{i+1})-I(t_{i})}{1}}=kI(t_{i})S(t_{i})-wI(t_{i})&\Leftrightarrow &I(t_{i+1})=I(t_{i})+kI(t_{i})S(t_{i})-wI(t_{i})\\\displaystyle {\frac {R(t_{i+1})-R(t_{i})}{1}}=wI(t_{i})&\Leftrightarrow &R(t_{i+1})=R(t_{i})+wI(t_{i})\\\end{array}}

%Entwicklung von S, I, R 
lockdown = 10;
for  i=1:t
    for g=1:Gebiete
        S(i+1,g)= S(i,g) - erkrankungsrate(g)*S(i,g)*I(i,g);
        I(i+1,g)= I(i,g) + erkrankungsrate(g)*S(i,g)*I(i,g) - genesungsrate*I(i,g);
        R(i+1,g)= R(i,g) + genesungsrate*I(i,g);
    endfor

if(i<=lockdown)    %es findet ein Lockdown an Tag i (hier Tag 10) statt, ab dem keine Bewegungen mehr in andere Gebiete möglich sind 
   Austausch = Austauschmatrix;
 else
   Austausch = 1;
 endif
   S(i+1,:)=S(i+1,:)*Austausch;    %gibt die neue Anzahl der Menschen in den Gebieten, die dorthin gewechselt haben (entsteht durch die alte Anzahl der Menschen mal Prozentanzahl der einzelnen Gebiete, wie viele Leute wechseln-> steht in Austauschmatrix) 
   I(i+1,:)=I(i+1,:)*Austausch;
   R(i+1,:)=R(i+1,:)*Austausch;
        
endfor

Plotten der Funktionen

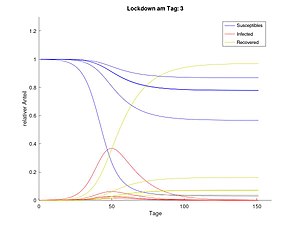
%Plotten der Funktionen für jedes Gebiet 
for g=1:Gebiete
  if(plotteInMehrereGrafiken == true)
    figure(g)   %für jeden Durchgang wird ein Bild erstellt 
  else
    figure(1)
  endif
  hold on
    plot(S(:,g), "color", [0 0 1])   %rgb macht Graph blau 
    plot(I(:,g), "color", [1 0 0])   %rgb -> rot 
    plot(R(:,g), "color", [0.8 0.8 0])   %rgb -> dunkelgelb 
  hold off

 axis([0 t+10 0 1.3])
 if (plotteInMehrereGrafiken)
   title(['Lockdown am Tag: ' num2str(lockdown) "  Gebiet: " num2str(g)]) %Ueberschrift der Grafik 
 else
    title(['Lockdown am Tag: ' num2str(lockdown) "  Alle Gebiete"]) %Ueberschrift der Grafik 
 endif
 legend('Susceptibles', 'Infected','Recovered')%Beschriftung der Funktionen 
 xlabel('Tage')  %Beschriftung der x-Achse 
 ylabel('relativer Anteil')  %Beschriftung der y-Achse 
 if(plotsAlsBilderSpeichern && !plotteInMehrereGrafiken)
   filename=["GLP_Modell_1b_Matrix_" num2str(matrix) "_Alle_Gebiete_Lockdown_" num2str(lockdown) ".jpg"];
   saveas((1), filename);
 elseif (plotsAlsBilderSpeichern && plotteInMehrereGrafiken)
   filename=["GLP_Modell_1b_Matrix_" num2str(matrix) "_Gebiet_" num2str(g) "_Lockdown_" num2str(lockdown) ".jpg"];
   saveas((g), filename);
 endif
       
endfor

Lockdown an Tag 1
Lockdown an Tag 3
Lockdown an Tag 5
Lockdown an Tag 10
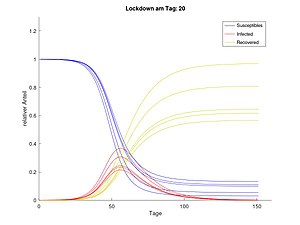
Lockdown an Tag 20
Lockdown an Tag 30
Lockdown an Tag 40
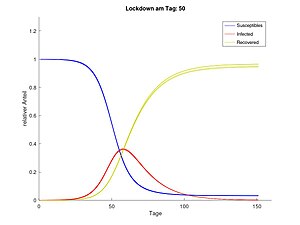
Lockdown an Tag 50

Ergebnis

Die Grafiken zeigen, dass es einen erheblichen Unterschied macht, wann der Lockdown geschieht. Je früher der Lockdown stattfindet, desto besser sind die Prognosen für die Gebiete 2,3,4 und 5. Je später eine solche Maßnahme der Virusbekämpfung erfolgt, desto höher ist die Belastung in allen Gebieten. Dies bedeutet in der Realität eine enorme Last für die Krankenhäuser zum selben Zeitpunkt und stellt somit eine Überlastung des Gesundheitssystems dar.

Reflexion des Modells

Abstände der einzelnen Gebiete zueinander wird nicht betrachtet.

Modell 2: SIR-Model mit Bewegungsfunktion

Abstandsfunktion

Diese Funktion gibt die Abstände von einem Punkt des Gitters, welcher durch die X und Y Indizes innerhalb des Gitters angegeben wird, zu allen anderen Gitterpunkten an. Diese Abstände werden in einer Matrix gespeichert und dann gewichtet, sodass die Spaltensummen jeweils $1$ ergeben.

$distance:(Mat(M\times N,\mathbb {R} ),\,y\in \{1,\dots ,M\}\subset \mathbb {N} ,\,x\in \{1,\dots ,N\}\subset \mathbb {N} )\rightarrow Mat(M\times N,[0,1]\subset \mathbb {R} )$
$(G,y,x)\mapsto distance(G,y,x)$

Beispiel

$(G:={\begin{pmatrix}g_{1,1}&g_{1,2}&g_{1,3}\\g_{2,1}&g_{2,2}&g_{2,3}\\g_{3,1}&g_{3,2}&g_{3,3}\\\end{pmatrix}},2,2)\mapsto distance(G,2,2)={\begin{pmatrix}0,31&0,25&0,31\\0,38&0,5&0,38\\0,31&0,25&0,31\\\end{pmatrix}}$

Umsetzung in Octave

function dist = distance (G,y_Coord,x_Coord)
... % Abfragen, ob die richtigen Parameter an die Funktion übergeben werden.
  X=columns(G);
  Y=rows(G);
  [x,y]=meshgrid(1:X,1:Y);
  if (y_Coord > 0 && y_Coord <= Y && x_Coord > 0 && x_Coord <= X)
  for j=1:Y
    for i=1:X
      dist(j,i)=sqrt((x_Coord-i)^2+(y_Coord-j)^2);
    endfor
  endfor
  w=1./(1+dist);
  ws=sum(w);
  dist=w./ws;
  else
    error(getDistance: Coordinates must be smaller than the size of the matrix")
  endif
...
endfunction

Bewegungsfunktion

Die Idee hinter der Bewegungsfunktion ist, dass man eine Matrix mit der Anzahl der Personen je Gitterpunkt an die Funktion übergibt und diese dann die Personen auf die Gitterpunkte verteilt. Nahe Gitterpunkte erhalten mehr Personen, als weiter Entfernte. Wichtig ist, dass die Anzahl an Personen (also die Summe der Matrizeneinträge) gleich bleibt.

$bewegung:Mat(M\times N,\mathbb {R} )\rightarrow Mat(M\times N,\mathbb {R} )$
$G\mapsto bewegung(G)$
$G$ entspricht einer Matrix mit der Anzahl der Personen je Gitterpunkt.

Umsetzung

Diese Funktion nutzt die vorher beschriebene Abstandsfunktion, um eine große Matrix zu erstellen $(abstand:=Mat(N\cdot M\times N\cdot M,[0,1]\subset \mathbb {R} ))$ . In dieser Matrix sind alle Abstände von allen Gitterpunkten enthalten. Die Matrix entsteht indem $N$ -viele $M\times N$ -Abstandsmatrizen untereinander angeordnet und $M$ -viele $M\times N$ -Abstandsmatrizen nebeneinander angeordnet werden.

  function erg = bewegung(G)
  ...
  N=columns(G);
  M=rows(G);
  [x,y]=meshgrid(1:N,1:M);
  for j=1:M
    for i=1:N
      abstand((i-1)*M+1:i*M,(j-1)*N+1:j*N)=distance(G,j,i);
      ... % Abfrage, ob das Ausführen der distance-Funktion funktioniert hat
    endfor
  endfor

Um nun die große Matrix mit allen Abstandswerten mit der übergebenen Gebietsmatrix zu verrechnen, wird die Gebietsmatrix in einen $N\cdot M$ -langen Spaltenvektor transformiert.

reshape(G',N*M,1)

Die Multiplikation der $N\cdot M\times N\cdot M$ -Matrix mit dem $N\cdot M\times 1$ -Spaltenvektor resultiert in einem $N\cdot M\times 1$ -Ergebnisvektor. Dieser wird anschließend wieder in eine $M\times N$ -Matrix zurück transformiert.

reshape(abstand*reshape(G',N*M,1),M,N)

Da die Spaltensummen der einzelnen distance-Matrizen $1$ sind und insgesamt $N$ -viele dieser Matrizen untereinanderstehen, sind die Spaltensummen der Abstandsmatrix jeweils N, sodass die Ergebnismatrix noch mit dem Faktor ${\frac {1}{N}}$ normiert werden muss.

erg=reshape(abstand*reshape(G',N*M,1),M,N)/N;

Die Bewegungsfunktion hat die Eigenschaft, dass sich die meisten Personen im Gitterzentrum sammeln. Am oberen und unteren Rand sind am wenigsten Personen.

Beispiel

$G:=Mat(24\times 24)$ mit $g_{i,j}=\left\{{\begin{array}{lcl}20&{\mbox{ für }}&i=j=3\\0&{\mbox{ sonst }}&\end{array}}\right.$
Tag 0: $G$
Tag 1: $bewegung(G)$
Tag 2: $bewegung(bewegung(G))$
Tag 3: $bewegung(bewegung(bewegung(G)))$

Tag 0
Tag 1
Tag 2
Tag 3

SIR-Modell mit einmaliger Bewegung

Die zuvor dokumentierte Bewegungsfunktion wird einmal zwischen den Zeitpunkten $t_{0}=0$ und $t_{1}=1$ ausgeführt.

GitterBreite = 24;
GitterHoehe = 24;
Koordinaten_Startgebiet = [3 3]; %In diesem Gebiet gibt es zum Zeitpunkt t0 Infizierte

M=GitterHoehe+1; % 1 höher wegen der Indizierung der Vektoren bzw. Matrizen in Octave
N=GitterBreite+1;
AnzahlGebiete = M * N; 

Tage = 200;

EinwohnerJeGebiet = 1000;
erkrankungsrate = 0.25;
genesungsrate = 1/14;

...

createSIR ist eine Funktion, welche die Matrizen $S,I$ und $R$ , analog zu Modell 1, sowie die dazugehörenden Startbedingungen erstellt.

[S,I,R] = createSIR(Tage, EinwohnerJeGebiet, Koordinaten_Startgebiet, M, N); %erstellt die S,I,R Matrizen analog zum ersten Modell
...
for  t=1:Tage
 tneu=t+1;
 for g=1:AnzahlGebiete
     S(tneu,g)= S(t,g) - erkrankungsrate*S(t,g)*I(t,g);
     I(tneu,g)= I(t,g) + erkrankungsrate*S(t,g)*I(t,g) - genesungsrate*I(t,g);
     R(tneu,g)= R(t,g) + genesungsrate*I(t,g);
 endfor
 
 S_Gebiet=reshape(S(tneu,:),M,N);
 I_Gebiet=reshape(I(tneu,:),M,N);
 R_Gebiet=reshape(R(tneu,:),M,N);
  
 Bewegungstage = [1 28 56]; % An diesen Tagen soll bewegung stattfinden
 if(lookup(sort(Bewegungstage),t,"b")) %ist t ein Element von Bewegungstage (nach Groeße sortiert), dann true, sonst false
 Bewegungstag = t; % zur Beschriftung benötigt

 S_Gebiet = bewegung(S_Gebiet);
 I_Gebiet = bewegung(I_Gebiet);
 R_Gebiet = bewegung(R_Gebiet);
 endif
 S(tneu,:) = reshape(S_Gebiet,1,M*N);
 I(tneu,:) = reshape(I_Gebiet,1,M*N);
 R(tneu,:) = reshape(R_Gebiet,1,M*N);

 S_inGebiet(tneu) = round(EinwohnerJeGebiet*sum(S(tneu,:)));
 I_inGebiet(tneu) = round(EinwohnerJeGebiet*sum(I(tneu,:)));
 R_inGebiet(tneu) = round(EinwohnerJeGebiet*sum(R(tneu,:)));

 I_max = max(I_inGebiet);

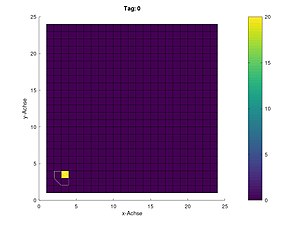
Plotten der Infizierten aller Gebiete zu allen Zeitpunkten.

 if(true)
   figure(t)
   surfc(I_Gebiet);
   %surface(I_Gebiet);
   title(["Infizierte der Gebiete - Bewegung zw. Tag: " num2str(Bewegungstag-1) " und " num2str(Bewegungstag)])
   text(-floor(6*N/10),floor(4*M/10),["Tag: " num2str(t) "\n" ... "%]"],"fontsize", 11)
   zlabel(["Anzahl Personen in " num2str(EinwohnerJeGebiet) " pro Gebiet"])
   axis([1 N 1 M 0 0.45])
   colormap('jet');
   colorbar ("SouthOutside")
   saveas((t),["Infizierte/GLP_Infizierte_Tag_" num2str(t) ".jpg"])
 endif
endfor

...

SIR-Modell mit ständiger Bewegung

Die zuvor dokumentierte Bewegungsfunktion wird zwischen allen Zeitpunkten $t_{i}=i,\,i\in \{0,...,T-1\}$ ausgeführt.

...
 
 S_Gebiet=reshape(S(tneu,:),M,N);
 I_Gebiet=reshape(I(tneu,:),M,N);
 R_Gebiet=reshape(R(tneu,:),M,N);

 Bewegungstage = 1:Tage; % An allen Tagen soll bewegung stattfinden
 if(lookup(sort(Bewegungstage),t,"b")) %ist t ein Element von Bewegungstage (nach groeße sortiert), dann true, sonst false
 Bewegungstag = t; %Bewegungstag = t, zur Beschriftung benötigt

 S_Gebiet = bewegung(S_Gebiet);
 I_Gebiet = bewegung(I_Gebiet);
 R_Gebiet = bewegung(R_Gebiet);
 endif

 S(tneu,:) = reshape(S_Gebiet,1,M*N);
 I(tneu,:) = reshape(I_Gebiet,1,M*N);
 R(tneu,:) = reshape(R_Gebiet,1,M*N);
 
 ...

Vergleich Bewegung zu unterschiedlichen Zeitpunkten und dauerhafter Bewegung

Modell 2: Vergleich; Infizierte pro Gebiet; Tag 1-200; 3-D

Reflexion des Modells

zentriertes Bewegungsmuster nicht realitätsnah
Bewegung führt dazu, dass bereits nach einem Gebietswechsel Bruchteile von Personen/ Infizierten in allen übrigen Gebieten sind
keine Berücksichtigung der epidemiologischen Abständen (nur geographische Abstände)

Ergänzungen Octave-Tutorial

Diese Ergänzungen wurden bei dem Octave-Tutorial ergänzt.

Matrix-Multiplikation in Octave - notwendig für die Modellierung diskreter Transportprozesse.

Literatur

Notieren Sie hier die von Ihnen verwendete Literatur

Boto von Querenburg (2013) Mengentheoretische Topologie - Springer-Lehrbuch

↑ UN-Guidelines for Use of SDG logo and the 17 SDG icons (2016/10) - http://www.un.org/sustainabledevelopment/wp-content/uploads/2016/10/UN-Guidelines-for-Use-of-SDG-logo-and-17-icons.October-2016.pdf
↑ UN-Guidelines for Use of SDG logo and the 17 SDG icons (2016/10) - http://www.un.org/sustainabledevelopment/wp-content/uploads/2016/10/UN-Guidelines-for-Use-of-SDG-logo-and-17-icons.October-2016.pdf
↑ UN-Guidelines for Use of SDG logo and the 17 SDG icons (2016/10) - http://www.un.org/sustainabledevelopment/wp-content/uploads/2016/10/UN-Guidelines-for-Use-of-SDG-logo-and-17-icons.October-2016.pdf

[1] UN-Guidelines for Use of SDG logo and the 17 SDG icons (2016/10) - http://www.un.org/sustainabledevelopment/wp-content/uploads/2016/10/UN-Guidelines-for-Use-of-SDG-logo-and-17-icons.October-2016.pdf

[2] UN-Guidelines for Use of SDG logo and the 17 SDG icons (2016/10) - http://www.un.org/sustainabledevelopment/wp-content/uploads/2016/10/UN-Guidelines-for-Use-of-SDG-logo-and-17-icons.October-2016.pdf

[3] UN-Guidelines for Use of SDG logo and the 17 SDG icons (2016/10) - http://www.un.org/sustainabledevelopment/wp-content/uploads/2016/10/UN-Guidelines-for-Use-of-SDG-logo-and-17-icons.October-2016.pdf

[1]

[2]

[3]