Kurs:Räumliche Modellbildung/Gruppe 4
Gruppenseite - HHL
[Bearbeiten]Diese Seite enthält die gesammelten Materialien der Gruppe 4 - HHL für die mündliche Portfolioprüfung im Mastermodul 11 - Mathematik an der Universität Landau.

Teilnehmer der Gruppe:
[Bearbeiten]- Lapport, Felix
- Herbrand, Tim
- Häßel, Tobias
Modellierungsthema
[Bearbeiten]Modellierungszyklen
[Bearbeiten]Modellierungszyklus I
[Bearbeiten]Programm
[Bearbeiten]Definition der Variablen
[Bearbeiten]Im ersten Schritt des Programms werden zunächst die Variablen definiert. Im Zuge dessen wird eine Matrix als Schachbrettmuster erstellt und die Positon eines oder mehrerer Infizierter am Tag 1 angegeben.
t = 19 ; %Zeiteinheiten (Tage) (eigentliche Tage - 2) A = zeros(15, 15); %Erstellung einer Matrix als Schachbrett A (7,6) = 2; %Position des ersten Infizierten %A (15,9) = 2; %Position des zweiten Infizierten [M N] = size (A); %Matrix größen I = 0 ; %Gesamtanzahl von Infizierten S = 0 ; %Gesamtanzahl von Empfänglichen R = 0 ; %Gesamtanzahl von Imunen
Programm
[Bearbeiten]Anschließend geht das Programm an jedem Tag alle Punkte durch und schaut dabei für jeden Punkt, ob ein Nachbar infiziert ist. Ist ein Nachbar infiziert, so wird der Punkt auch angesteckt.
Jeder einzelne Punkt der Matrix wird angeschaut falls dieser infiziert ist werden die Nachbarn infiziert. Besonderheit, nur wenn er frisch infiziert ist, infiziert er seine Nachbarn.
%Alle um den Infizierten werden angesteckt
if A(m,n) == 0
hold on
elseif A(m,n) == 2
if A(m+1 ,n+1) < 2
A(m+1 ,n+1) = 1 ;
endif
if A(m+1 ,n-1) < 2
A(m+1 ,n-1) = 1 ;
endif
if A(m+1 ,n) < 2
A(m+1 ,n) = 1 ;
endif
if A(m ,n+1) < 2
A(m ,n+1) = 1 ;
endif
if A(m ,n-1) < 2
A(m ,n-1) = 1 ;
endif
if A(m-1 ,n) < 2
A(m-1 ,n) = 1 ;
endif
if A(m-1 ,n+1) < 2
A(m-1 ,n+1) = 1 ;
endif
if A(m-1 ,n-1) < 2
A(m-1 ,n-1) = 1 ;
endif
Die infizierten werden um einen Tag erhöht und sobald sie die 14 Tage überschreiten bekommen sie den Wert 99 um zu signalisieren, dass sie wieder gesund sind.
%Infizierte Tage
if A(m,n) == 14
A(m,n) = 99 ;
endif
if A(m,n) >=2 && A(m,n) <= 14
A(m,n) = A(m,n) + 1 ;
elseif A(m,n) == 0
hold on
endif
Da wir einen erst Infizierten gebraucht haben ist dieser mit dem Wert 1 versehen. Somit beginnen wir an Tag 1 mit dem Wert zwei. (im späteren Verlauf wurden die Werte der Matrix vor der Ausgabe um 1 reduziert, um einem Missverstädnis entgegen zu wirken.
%neuinfizierte zu altinfizierte
for m = 1:M
for n = 1:N
if A(m,n) == 1
A(m,n) = 2 ;
elseif A(m,n) == 0
hold on
endif
endfor
endfor
%Anzahl Infizierte werden gezählt
if A(m,n) >= 2 && A(m,n) <= 14
I = I+1 ;
elseif A(m,n) == 0
S = S + 1 ;
elseif A(m,n) == 99
R = R + 1 ;
endif
Ausgabe des Programms
[Bearbeiten]Ausgangsmatrix
[Bearbeiten]In der Ausgangsmatrix A ist eine Person infiziert (2er) und zwar der Punkt (7,6). Alle anderen Punkte/Personen sind noch nicht Infiziert (0er).
A =
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 2 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Nun wird für jeden Tag und für jeden Punkt geschaut, ob ein Nachbarpunkt infiziert ist und falls ja, der Punkt ebenfalls infiziert. Im Fall von Tag 1 werden daher alle Nachbarpunkte von (7,6) neu infiziert, sie werden daher auf eine 2 gestellt. Die Infizierten Personen/Punkte vom Tag 1 werden um eine Zahl höher gestellt, das heißt sie sind jetzt eine 3. Außerdem wird für jeden Tag die Anzahl der Susceptible (S),Infected (I) und Removed (R) ausgegeben. Am ersten Tag gehören 216 Personen zur Gruppe der Susceptible, 9 Personen sind infiziert und noch keine Person genesen.
Tag = 1
A =
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 2 2 2 0 0 0 0 0 0 0 0
0 0 0 0 2 3 2 0 0 0 0 0 0 0 0
0 0 0 0 2 2 2 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
S = 216
I = 9
R = 0
Ist eine Person 14 Tage infiziert gewesen, so ist sie nun gesund. Das bedeutet, sobald eine Person eigentlich auf eine 15 gestellt wird, wird sie nun auf eine 99 gestellt. Die 99 steht dabei für eine genesene Person. In diesem Beispiel ist die Person (7,6) am 13. Tag genesen, sie ist seit Tag 0 infiziert und damit 14 Tage infiziert gewesen.
Tag = 13
A =
9 9 9 9 9 9 9 9 9 9 9 9 8 7 6
10 10 10 10 10 10 10 10 10 10 10 9 8 7 6
10 11 11 11 11 11 11 11 11 11 10 9 8 7 6
10 11 12 12 12 12 12 12 12 11 10 9 8 7 6
10 11 12 13 13 13 13 13 12 11 10 9 8 7 6
10 11 12 13 14 14 14 13 12 11 10 9 8 7 6
10 11 12 13 14 99 14 13 12 11 10 9 8 7 6
10 11 12 13 14 14 14 13 12 11 10 9 8 7 6
10 11 12 13 13 13 13 13 12 11 10 9 8 7 6
10 11 12 12 12 12 12 12 12 11 10 9 8 7 6
10 11 11 11 11 11 11 11 11 11 10 9 8 7 6
10 10 10 10 10 10 10 10 10 10 10 9 8 7 6
9 9 9 9 9 9 9 9 9 9 9 9 8 7 6
8 8 8 8 8 8 8 8 8 8 8 8 8 7 6
7 7 7 7 7 7 7 7 7 7 7 7 7 7 6
S = 0
I = 224
R = 1
Aufgetretene Probleme
[Bearbeiten]In diesem Modell finden sich einige Probleme, die beachtet und in einem neuen Modell optimiert werden müssen. Dazu gehört zum Beispiel:
- Bewegung: In dem Modell fehlt die Bewegung, aktuell sind alle Personen fest an ihrem Ort.
- Jeder Nachbarpunkt wird automatisch infiziert, sodass die Berücksichtigung des Abstandes fehlt.
Modellierungszyklus II
[Bearbeiten]Programm
[Bearbeiten]Definition der Grundparameter
[Bearbeiten]Im ersten Schritt des Modells werden die wichtigsten Paramater (Tage, Matrixgröße, Ansteckungsabstand, Bewegungsgeschwindigkeit) definiert und eine mxn-Matrix aus Nullen erstellt. Außerdem wird die Position eines ersten Infizierten angegeben und Infizierte durch eine 2 im Modell kenntlich gemacht. In dem Modell stellen alle Nullen die Immunen dar, das heißt die Gruppe der Susceptible. Diese sind noch für eine Infektion mit dem Corona-Virus empfänglich.
t = 19 ; %Zeiteinheiten (Tage) (eigentliche Tage - 2) A = zeros(15, 15); %Erstellung einer Matrix als Schachbrett %A (1,6) = 2; %Position des ersten Infizierten %A (14,9) = 2; %Position des zweiten Infizierten [M N] = size (A); %Matrix größen A(ceil(rand(1,1)*15),ceil(rand(1,1)*5)) = 2; %Zufällige Position des ersten Infizierten I = 0 ; %Gesamtanzahl von Infizierten S = 0 ; %Gesamtanzahl von Empfänglichen R = 0 ; %Gesamtanzahl von Imunen AnsteckungsAbstand = 1.5 ; %Ansteckungsabstand festlegen Bewegungsgeschwindigkeit = 2 ; %Geschwindigkeit der einzelnen Pazellen
Im nächsten Schritt erzeugen wir zufällige Positionen in Abhängigkeit der vorgegebenen Matrixgröße:
X = rand(M,N); X = X*M; %Abstand in x-Richtung Y = rand(M,N); Y = Y*N; %Abstand in y-Richtung
Schleifen
[Bearbeiten]Unter der Hauptschleife, die quasi für jeden Tag einmal durchläuft gibt es noch folgende Schleifen:
Schleife 1
[Bearbeiten]Die folgende Schleife wird für jeden einzelnen Tag erneut durchlaufen. Dabei wird an jedem einzelnen Tag der Abstand zwischen einem Punkt und den infizierten Punkten verglichen. Für diese Schleife wird auch die 1. Funktion (Abstandvergleichen) benötigt.
Infiziermatrix = zeros(15,15); %Matrix der am Tag neuifizierten X = Bewegung(A, Bewegungsgeschwindigkeit, X); %zufällige Bewegung in x-Richtung an dem Tag i Y = Bewegung(A, Bewegungsgeschwindigkeit, Y); %zufällige Bewegung in y-Richtung an dem Tag i for m = 1:M %jeder Punkt wird einzeln durchgegangen for n = 1:N if A(m,n) >= 2 %nur die infizierten Punkte werden angeschaut %Der Abstand jedes einzelnen Punktes wird mit dem Infizierten Punkt verglichen und sobald der %Abstand zu gering ist, wird er in die Infiziermatrix eingetragen Infiziermatrix = Infiziermatrix + Abstandvergleichen(A,m,n,X,Y,M,N,AnsteckungsAbstand) ; %Da ein Punkt von mehreren Leuten infiziert werden kann und sich somit addiert... %werden die positiven Werte der Infiziermatrix auf 1 gesetzt. Infiziermatrix = Matrix_eintraege_eins(Infiziermatrix,M,N); endif endfor endfor A = A + Infiziermatrix; %Übertragung der neuinfizierten in die eigentliche Matrix
Schleife 2
[Bearbeiten]Hier werden die Infizierten um einen Tag erhöht und die Geheilten mit einer 16 markiert .
%Infizierte Tage for m = 1:M %Jeder einzelne Punkt wird angeschaut for n = 1:N if A(m,n) >= 15 %Alle Punkte, die länger als 15 Tage infiziert waren sind geheilt A(m,n) = 16 ; %und auf 16 gesetzt 16 steht für geheilt endif if A(m,n) >=2 && A(m,n) <= 15 %Alle Infizierten A(m,n) = A(m,n) + 1 ; %deren Tag der Infizierung wird um eins erhöht endif endfor endfor
Schleife 3
[Bearbeiten]In dieser Schleife werden die neuinfizierten zu Infizierten.
(vgl. erstes Modell)
%neuinfizierte zu altinfizierte for m = 1:M %Jeder Punkt wird durchgegangen for n = 1:N if A(m,n) == 1 %Neuinfizierte A(m,n) = 2 ; %werden zu Altinfizierte elseif A(m,n) == 0 %mit Gesunden passiert nix hold on endif endfor endfor
Schleife 4
[Bearbeiten]Diese Schleife setzt alle Werte der Matrix, die INfiziert wurden um eins herunter, da wir bei 2 beginnen zu zählen (siehe Schleife 3).
Somit stimmen die werte der ausgegebenen Matrix mit den infizierten Tagen überein.
Endmatrix = A; for m = 1:M %Jeder Punkt wird angeschaut for n = 1:N if A(m,n) >=2 && A(m,n) ~= 16 Endmatrix(m,n) = Endmatrix(m,n) - 1 ; %da neuifizierte mit 1 anfangen ist jeder Zahl eins zu hoch endif %so muss jeder Wert (bis auf die 0er) um eins veringert werden endfor endfor
Funktionsdefinitionen
[Bearbeiten]Funktion "Wer steckt sich Abstandsbedingt an?"
[Bearbeiten]function wert=Abstandvergleichen(A,m,n,X,Y,M,N,AnsteckungsAbstand) AnsteckungsMatrix = zeros(M,N); %Matrix zum ausfüllen der Infizierten wird implementiert for m1 = 1:M %Jeder Punkt wird angeschaut for n1 = 1:N %Jeder Abstand wird nachgeprüft und mit dem Infektionsradius verglichen if sqrt(abs(X(m1,n1)-X(m,n))^2 + (abs(Y(m1,n1)-Y(m,n)))^2) < AnsteckungsAbstand && m1 ~= m && n1 ~= n && A(m1,n1) == 0 AnsteckungsMatrix(m1,n1) = 1; %Falls der Abstand zu klein ist, wird er angesteckt und in der Matrix eingetragen endif endfor endfor wert = AnsteckungsMatrix ; endfunction
Hier wird eine Matrix ausgegeben, die die Punkte Ausgibt, die sich an dem Tag angesteckt haben.
Funktion "zufällige Bewegung der Punkte"
[Bearbeiten] function wert = Bewegung(Matrix, Geschwindigkeit, X)
[M N] = size (Matrix) ;
for m = 1:M
for n = 1:N
X(m,n) = X(m,n) + (rand-0.5)*2 * Geschwindigkeit ;
endfor
endfor
wert = X ;
endfunction
Hier bekommen die Werte der Positionsmatrix neue Werte, je nach angegebener Bewegungsgeschwindigkeit. Diese muss einmal für die Y-Werte und einmal für die X-Werte ausgeführt werden.
Funktion "Hilfsfunktion für die Anstreckungsfunktion"
[Bearbeiten] function wert = Matrix_eintraege_eins(A,M,N)
for m2 = 1:M
for n2 = 1:N
if A(m2,n2) >= 1
A(m2,n2) = 1;
endif
endfor
endfor
wert = A ;
endfunction
Mit dieser Funktion werden alle Werte die nicht null sind auf den Wert 1 gesetzt.
Ausgabe des Programmes
[Bearbeiten]Ausgabe der Ausgangsmatrix:
A =
0 0 0 0 0 2 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
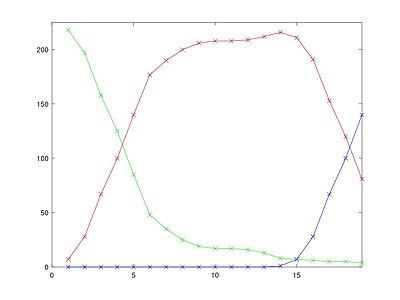
Im Folgenden werden Beispiele des Punktegitters an verschiedenen Tagen dargestellt:
Am ersten Tag sieht die Ausgabematrix wie folgt aus:
Tag = 1
Endmatrix =
0 0 0 0 0 2 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
S = 218
I = 7
R = 0
Am ersten Tag sind 7 Personen infiziert. 218 Personen sind Infektionsanfällig (Susceptible).
Es ist auch zusätzlich zu beachten, dass die Position der Punkte in keinem Zusammenhang zu der Position in der Matrix stehen.
Die Position wird unabhängig in einer X und Y Matrix gespeichert.
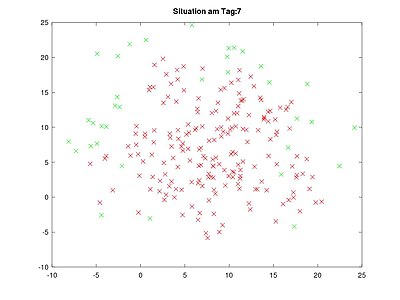
Am siebten Tag sind 190 Personen infiziert und 35 Personen sind noch infektionsanfällig. Bereits genesen ist noch niemand (R).
Tag = 7
Endmatrix =
2 5 0 6 3 8 4 4 1 4 6 3 3 3 0
6 5 0 2 3 0 5 3 0 6 4 3 0 5 3
3 0 0 0 3 6 5 2 6 5 5 5 6 2 3
2 4 5 2 0 0 6 0 0 0 3 2 6 4 7
0 3 6 4 2 5 2 5 3 5 5 2 1 0 3
3 4 3 2 5 3 1 4 5 4 6 7 2 7 5
4 0 4 0 5 0 3 0 0 5 5 3 4 3 2
2 2 2 6 6 5 5 0 5 5 3 6 0 5 2
3 6 4 6 3 3 2 2 0 5 4 1 5 2 7
3 4 0 2 1 2 4 0 4 3 0 3 7 1 3
4 2 6 0 1 0 4 3 4 2 4 4 5 2 2
0 1 2 2 3 0 4 2 5 4 2 5 4 3 3
4 0 1 5 3 0 4 2 5 5 2 5 6 1 2
4 5 6 2 5 3 1 3 2 3 5 5 1 5 7
0 0 2 6 3 2 1 4 3 4 5 4 4 6 3
S = 35
I = 190
R = 0
Tag = 14
Endmatrix =
9 12 6 13 10 16 11 11 8 11 13 10 10 10 6
13 12 7 9 10 7 12 10 0 13 11 10 0 12 10
10 0 2 0 10 13 12 9 13 12 12 12 13 9 10
9 11 12 9 7 1 13 7 2 6 10 9 13 11 14
2 10 13 11 9 12 9 12 10 12 12 9 8 0 10
10 11 10 9 12 10 8 11 12 11 13 14 9 14 12
11 7 11 6 12 6 10 7 1 12 12 10 11 10 9
9 9 9 13 13 12 12 5 12 12 10 13 0 12 9
10 13 11 13 10 10 9 9 1 12 11 8 12 9 14
10 11 5 9 8 9 11 7 11 10 6 10 14 8 10
11 9 13 1 8 3 11 10 11 9 11 11 12 9 9
0 8 9 9 10 7 11 9 12 11 9 12 11 10 10
11 7 8 12 10 1 11 9 12 12 9 12 13 8 9
11 12 13 9 12 10 8 10 9 10 12 12 8 12 14
7 0 9 13 10 9 8 11 10 11 12 11 11 13 10
S = 8
I = 216
R = 1
Tag = 18
Endmatrix =
13 16 10 16 14 16 16 16 12 16 16 14 14 14 10
16 16 11 13 14 11 16 14 0 16 16 14 0 16 14
14 3 6 0 14 16 16 13 16 16 16 16 16 13 14
13 16 16 13 11 5 16 11 6 10 14 13 16 16 16
6 14 16 16 13 16 13 16 14 16 16 13 12 0 14
14 16 14 13 16 14 12 16 16 16 16 16 13 16 16
16 11 16 10 16 10 14 11 5 16 16 14 16 14 13
13 13 13 16 16 16 16 9 16 16 14 16 2 16 13
14 16 16 16 14 14 13 13 5 16 16 12 16 13 16
14 16 9 13 12 13 16 11 16 14 10 14 16 12 14
16 13 16 5 12 7 16 14 16 13 16 16 16 13 13
0 12 13 13 14 11 16 13 16 16 13 16 16 14 14
16 11 12 16 14 5 16 13 16 16 13 16 16 12 13
16 16 16 13 16 14 12 14 13 14 16 16 12 16 16
11 4 13 16 14 13 12 16 14 16 16 16 16 16 14
S = 5
I = 120
R = 100

Ergänzungen Octave-Tutorial
[Bearbeiten]Diese Ergänzungen wurden bei dem Octave-Tutorial vorgenommen, um die Implementation der Gruppe bzgl. der verwendeten Octave-Befehle nachvollziehbar zu machen.
- Matrix-Multiplikation in Octave - notwendig für die Modellierung diskreter Transportprozesse.
Skripte in Octave
[Bearbeiten]Referenzieren Sie hier die von Ihnen verwendeten Skripte und Bibliotheken in Octave oder R/Studio
Literatur
[Bearbeiten]Notieren Sie hier die von Ihnen verwendete Literatur
- Boto von Querenburg (2013) Mengentheoretische Topologie - Springer-Lehrbuch