Kurs:Statistik für Anwender/Bedingte Wahrscheinlichkeiten

Bedingte Wahrscheinlichkeiten

Motivation I

Ein Ereignis ${\textstyle B}$ hat (in einem gegebenen W-Raum) eine bestimmte Wahrscheinlichkeit ${\textstyle P(B)}$. Liegt eine zusätzliche Information vor — d.h. man weiß dass ein weiteres Ereignis ${\textstyle A}$ tatsächlich eingetreten ist — so kann sich die Wahrscheinlichkeitseinschätzung für ${\textstyle B}$ ändern. Anstatt ${\textstyle P(B)}$ betrachtet man nun die bedingte Wahrscheinlichkeit ${\textstyle P(B|A)}$.
In vielen Situationen sind die vorliegenden Informationen und/oder die interessierende(n) Größe(n) Werte bestimmter bedingter Wahrscheinlichkeiten.

Motivation II

Zur Behandlung solcher Fragen ist dann einerseits die Modellierung der Situation (Welche bedingten Wahrscheinlichkeiten sind gegeben bzw. gesucht?) und andererseits der mathematisch korrekte Umgang mit bedingten Wahrscheinlichkeiten erforderlich (Wie kommt man rechnerisch zur Lösung?). Eine wichtige Anwendung ist die Interpretation von Testergebnissen.
Die Arbeit mit bedingten Wahrscheinlichkeiten führt uns auch zur Aufstellung von Baumdiagrammen, mit denen Wahrscheinlichkeiten oft auch ohne die (aufwändige) Aufstellung eines W-Raumes bestimmt werden können.
Hinweis: Für das Gegenereignis ${\textstyle \Omega \setminus A}$ schreiben wir ab sofort auch ${\textstyle {\overline {A}}}$.

Definition Bedingte Wahrscheinlichkeiten

Ist ${\textstyle (\Omega ,P)}$ ein W-Raum und sind ${\textstyle A,B\in {\mathcal {P}}}$ mit ${\textstyle P(A)>0}$, so nennt man
$$P(B|A)={\frac {P(A\cap B)}{P(A)}}\in [0,1]$$
die bedingte Wahrscheinlichkeit von ${\textstyle B}$ unter der Bedingung ${\textstyle A}$.

Eigenschaften Bedingte Wahrscheinlichkeit

Sie hat die folgenden elementaren Eigenschaften:

• Es gilt ${\textstyle P(A|A)=1}$ und ${\textstyle P(B|A)=0}$ für ${\textstyle A\cap B=\emptyset }$.
• Es gilt ${\textstyle P(B|\Omega )=P(B)}$.
• Für ${\textstyle B\subseteq A}$ gilt ${\textstyle P(B|A)={\frac {P(B)}{P(A)}}}$ und ${\textstyle P(A|B)=1}$.
• Meist gilt ${\textstyle P(A|B)\not =P(B|A)}$.

Die bedingte Wahrscheinlichkeit ${\textstyle P(B|A)}$ gibt die Wahrscheinlichkeit dafür an, dass ${\textstyle B}$ eintritt, wenn bekannt ist, dass ${\textstyle A}$ eintritt.

Beispiele

Beispiel 1.1

Jemand erwartet einen Brief, der innerhalb einer Woche (an einem der Tage Montag-Freitag) zugestellt werden soll. Er schätzt, dass er den Brief mit der Wahrscheinlichkeit ${\textstyle p=0.6}$ überhaupt erhält (und zwar an jedem Tag mit der gleichen Wahrscheinlichkeit). Ein geeignete Ergebnismenge ist ${\textstyle \Omega =\{{\text{mo, di, mi, do, fr, nicht}}\}}$ mit den folgenden (subjektiven) Wahrscheinlichkeitseinschätzungen für die Ergebnisse: ${\textstyle p_{\text{mo}}=0.12,\quad p_{\text{di}}=0.12,\quad p_{\text{mi}}=0.12,\quad p_{\text{do}}=0.12,}$
${\textstyle p_{\text{fr}}=0.12,\quad p_{\text{nicht}}=0.4}$
Das Ereignis ${\textstyle A:}$ " Er erhält den Brief ". entspricht dann der Menge
$$A=\{{\text{mo, di, mi, do, fr}}\}\subseteq \Omega \quad {\text{mit}}\quad P(A)=0.6$$

Beispiel 1.2

Angenommen, er hat den Brief am Montag noch nicht erhalten. Dann ist bekannt, dass das Ereignis ${\textstyle B_{1}=\{{\text{di, mi, do, fr, nicht}}\}}$ eintritt. Es gilt:
$$\left.{\begin{array}{rclcl}P(B_{1})&=&0.88\\P(A\cap B_{1})&=&0.48\end{array}}\right\}\quad$$
$$\rightarrow \quad P(A|B_{1})=0.544$$
Mit einer Wahrscheinlichkeit von ${\textstyle 0.544}$ wird er den Brief also noch erhalten.

Beispiel 1.3

Angenommen, er hat den Brief am Dienstag noch nicht erhalten. Dann ist bekannt, dass das Ereignis ${\textstyle B_{2}=\{{\text{mi, do, fr, nicht}}\}}$ eintritt. Es gilt: $$\left.{\begin{array}{rclcl}P(B_{2})&=&0.76\\P(A\cap B_{2})&=&0.36\end{array}}\right\}\quad$$
$$\rightarrow \quad P(A|B_{2})=0.474$$
Mit einer Wahrscheinlichkeit von ${\textstyle 0.474}$ wird er den Brief also noch erhalten.

Beispiel 1.4

Angenommen, er hat den Brief am Mittwoch noch nicht erhalten. Dann ist bekannt, dass das Ereignis ${\textstyle B_{3}=\{{\text{do, fr, nicht}}\}}$ eintritt. Es gilt: $$\left.{\begin{array}{rclcl}P(B_{3})&=&0.64\\P(A\cap B_{3})&=&0.24\end{array}}\right\}\quad$$
$$\rightarrow \quad P(A|B_{3})=0.375$$
Mit einer Wahrscheinlichkeit von ${\textstyle 0.375}$ wird er den Brief also noch erhalten.

Beispiel 1.5

Angenommen, er hat den Brief am Donnerstag noch nicht erhalten. Dann ist bekannt, dass das Ereignis ${\textstyle B_{4}=\{{\text{fr, nicht}}\}}$ eintritt. Es gilt:
$$\left.{\begin{array}{rclcl}P(B_{4})&=&0.52\\P(A\cap B_{4})&=&0.12\end{array}}\right\}\quad \rightarrow \quad P(A|B_{4})=0.231$$
Mit einer Wahrscheinlichkeit von ${\textstyle 0.231}$ wird er den Brief also noch erhalten.

Beispiel 1.6

Angenommen, er hat den Brief am Freitag noch nicht erhalten. Dann ist bekannt, dass das Ereignis ${\textstyle B_{5}=\{{\text{nicht}}\}}$ eintritt. Es gilt:
$$\left.{\begin{array}{rclcl}P(B_{5})&=&0.4\\P(A\cap B_{5})&=&0\end{array}}\right\}\quad \rightarrow \quad P(A|B_{5})=0$$
Mit einer Wahrscheinlichkeit von ${\textstyle 0}$ wird er den Brief also noch erhalten.

Beispiel 2

Ein Student stellt sich zur Vorlesung einen Wecker. Mit einer Wahrscheinlichkeit von ${\textstyle p=0.6}$ wird er vom Klingeln des Weckers wach. Falls er wach wird, erreicht er mit einer Wahrscheinlichkeit von ${\textstyle p=0.8}$ rechtzeitig die Vorlesung. Wie groß ist insgesamt die Chance, dass er es rechtzeitig zur Vorlesung schafft.

Wir betrachten die Ereignisse
${\textstyle \quad \quad A:}$" Er wird wach." und ${\textstyle \quad B:}$ " Er erreicht rechtzeitig die Vorlesung."
Bekannt ist ${\textstyle P(A)=0.6}$ und ${\textstyle P(B|A)=0.8}$. Gesucht ist ${\textstyle P(B)}$.
$$\quad P(B)=0.48$$

Beispiel 3.1

Falls es trocken ist, gewinnt ein Rennfahrer das nächste Rennen mit einer Wahrscheinlichkeit von 20%. Bei Regen hat er sogar eine Siegchance von 50%. Laut Wettervorhersage beträgt die Regenwahrscheinlichkeit 40%.

• Wie wahrscheinlich sollte nach diesen Vorgaben ein Sieg des Rennfahrers sein? (Wir schreiben: ${\textstyle R:}$Regen und ${\textstyle S:}$Sieg)
  $${\begin{aligned}P(S)=0.32\end{aligned}}$$

Beispiel 3.2

• Jemand erfährt, dass der Rennfahrer gewonnen hat. Wie groß, ist demnach die Wahrscheinlichkeit, dass es geregnet hat?
  $${\text{Gesucht ist:}}\quad P(R|S)=0.625$$

Aufgaben

Aufgabe I

Geben Sie im Folgenden die angegebenen Informationen und die gesuchten Werte als Wahrscheinlichkeiten ${\textstyle P(\ldots )}$ bzw. als bedingte Wahrscheinlichkeiten ${\textstyle P(\ldots |\ldots )}$ an:
Jeder vierte Bewohner eines Ortes besitzt einen Garten. ${\textstyle 60\%}$ der Gartenbesitzer haben ein Haustier, von den Übrigen haben nur ${\textstyle 20\%}$ ein Haustier.

• Wie hoch ist der Anteil der Bewohner, die ein Haustier besitzen?
• Wie hoch ist der Anteil der Gartenbesitzer unter denen, die ein Haustier besitzen? Wie hoch ist der Anteil der Gartenbesitzer unter denen, die kein Haustier besitzen?

Aufgabe II

Bei einer Quizsendung muss ein Kandiat eine der vier Antwortmöglichkeiten ${\textstyle A,B,C,D}$ raten. Er schätzt folgende Wahrscheinlichkeiten für die Antworten: $$P(\{A\})=0.3,\quad P(\{B\})=0.4,\quad P(\{C\})=0.05,\quad P(\{D\})=0.25$$

• Der Moderator verrät ihm, dass Antwort ${\textstyle B}$ falsch ist. Welche Wahrscheinlichkeiten weist der Kandidat nun den einzelnen Antworten (sinnvollerweise) zu?
• Durch den Einsatz eines "Jokers" erfährt der Kandidat, dass eine der beiden Antworten ${\textstyle A}$ und ${\textstyle C}$ richtig ist. Welche Wahrscheinlichkeiten weist der Kandidat nun diesen beiden Antworten (sinnvollerweise) zu?

Aufgabe III

Gegeben seien ein weißer und ein schwarzer Laplace-Würfel.

1. Bestimmen Sie die Wahrscheinlichkeit dafür, dass der schwarze Würfel eine 6 zeigt unter der Bedingung, dass die Augensumme der Würfel 11 ist.
2. Bestimmen Sie die Wahrscheinlichkeit dafür, dass der weiße Würfel eine 5 zeigt unter der Bedingung, dass die Augensumme der Würfel 4 ist.
3. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die Augensumme der Würfel 7 ist unter der Bedingung, dass die Augenzahl des schwarzen Würfels kleiner als die des weißen Würfels ist.

Aufgabe IV

Insgesamt kommen ${\textstyle 80\%}$ aller Hörer einer Vorlesung pünktlich, unter denjenigen, die mit dem Auto kommen sind es sogar ${\textstyle 95\%}$. Zusätzlich sei bekannt, dass insgesamt ${\textstyle 30\%}$ der Hörer mit dem Auto kommen. Wie groß ist der Anteil der Autofahrer

• unter den Pünktlichen?

• unter denjenigen, die zu spät kommen?

Aufgabe V

Bei einer Telefonberatung arbeiten ${\textstyle 5}$ verschiedene Berater ${\textstyle B_{1},\ldots ,B_{5}}$. Sie bearbeiten unterschiedliche Anteile der Anfragen und haben verschiedene Quoten bezüglich der Zufriedenheit der Kunden:

$${\begin{array}{|c|c|c|c|c|c|}\hline {\text{Berater}}&B_{1}&B_{3}&B_{3}&B_{4}&B_{5}\\\hline {\text{bearbeitet den folgenden Anteil der Anfragen}}&0.15&0.2&0.2&0.4&0.05\\\hline {\text{Anteil der zufriedenen Kunden bei diesem Berater}}&0.2&0.8&0.4&0.7&0.9\\\hline \end{array}}$$

• Wie hoch ist der Anteil der zufriedenen Kunden insgesamt?

• Berechnen Sie den Anteile der verschiedenen Beratern unter den zufriedenen Kunden bzw. unter den unzufriedenen Kunden.

Stochastische Unabhängigkeit

Definition Stochastische Unabhängigkeit

Sei ${\textstyle (\Omega ,P)}$ ein W-Raum. Zwei Ereignisse ${\textstyle A,B\in {\mathcal {P}}}$ mit ${\textstyle P(A),P(B)>0}$ heißen (stochastisch) unabhängig, falls die folgenden äquivalenten Bedingungen erfüllt sind: ${\textstyle \quad P(B|A)=P(B)\ \Leftrightarrow \ P(A|B)=P(A)\ \Leftrightarrow \ P(A\cap B)=P(A)\cdot P(B)}$

Beispiel I

Ein Würfel wird einmal geworfen. Wir betrachten die Ergebnismenge ${\textstyle \Omega =\{1,\ldots ,6\}}$ und die Ereignisse: ${\textstyle \quad A=\{3,4,5,6\},\ B=\{1,2,3,4,5\},\ C=\{1,3,5\}}$
Dann gilt:

• ${\textstyle P(A|B)={\frac {3}{5}}\quad {\text{und}}\quad P(B|A)={\frac {3}{4}}}$
  Wegen ${\textstyle P(A|B)\not =P(A)}$ bzw. ${\textstyle P(B|A)\not =P(B)}$ sind ${\textstyle A,B}$ nicht unabhängig.
• ${\textstyle P(A|C)={\frac {2}{3}}\quad {\text{und}}\quad P(C|A)={\frac {1}{2}}}$
  Wegen ${\textstyle P(A|C)=P(A)}$ bzw. ${\textstyle P(C|A)=P(C)}$ sind ${\textstyle A,C}$ unabhängig.
• ${\textstyle P(B|C)=1\quad {\text{und}}\quad P(C|B)={\frac {3}{5}}}$
  Wegen ${\textstyle P(C|B)\not =P(C)}$ bzw. ${\textstyle P(B|C)\not =P(B)}$ sind ${\textstyle B,C}$ nicht unabhängig.
  

Beispiel II

Man würfelt mit drei Würfeln und interessiert sich für die Wahrscheinlichkeit des Ereignisses:
${\textstyle A:}$ " Alle drei Würfel zeigen die Augenzahl 6 "
Offenbar ist ${\textstyle A=A_{1}\cap A_{2}\cap A_{3}\quad }$
wobei: ${\textstyle A_{i}}$:" Der i-te Würfel zeigt eine 6 ." (i=1,2,3)
Da ${\textstyle A_{1},A_{2},A_{3}}$ unabhängig voneinander sind und jeweils die Wahrscheinlichkeit ${\textstyle {\frac {1}{6}}}$ haben, folgt:
${\textstyle \quad P(A)=P(A_{1}\cap A_{2}\cap A_{3})=P(A_{1})\cdot P(A_{2})\cdot P(A_{3})={\frac {1}{6}}\cdot {\frac {1}{6}}\cdot {\frac {1}{6}}={\frac {1}{216}}}$

Beispiel III

Zwei unzuverlässige Personen verabreden sich. Für die Ereignisse
${\textstyle A:{\text{'' Person 1 erscheint zum Treffen. ''}}\quad {\text{und}}}$
${\textstyle B:{\text{'' Person 2 erscheint zum Treffen. ''}}}$
geht man von den Wahrscheinlichkeiten ${\textstyle P(A)=0.8}$ und ${\textstyle P(B)=0.9}$ aus. Falls beide Personen unabhängig voneinander zum Treffen erscheinen (d.h. falls bekannt ist, dass eine Person kommt, ändert sich die Wahrscheinlichkeit, dass die Andere ebenfalls kommt, nicht) folgt:
${\textstyle \quad P(A\cap B)=P(A)\cdot P(B)=0.8\cdot 0.9=0.72}$

Beispiel IV

Von den Ereignissen ${\textstyle A:{\text{'' Es ist Sonntag. ''}}\quad B:{\text{'' Es regnet. ''}}\quad C:{\text{'' Person 1 geht ins Freibad. ''}}}$
${\textstyle D:{\text{'' Person 2 geht ins Kino.''}}}$ (für einen zufälligen Tag)
sind wohl nur ${\textstyle A}$ und ${\textstyle B}$ stochastisch unabhängig.

Aufgabe 1.1

Ein roter und ein blauer Würfel werden geworfen. Geben Sie eine Ergebnismenge ${\textstyle \Omega }$ an, bezüglich der dieses ZE ein Laplace-Experiment ist. Beschreiben Sie die folgenden Ereignisse als Teilmenge von ${\textstyle \Omega }$ und berechnen Sie ihre Wahrscheinlichkeit:

${\textstyle A}$: ${\textstyle {\text{''Der rote Würfel zeigt eine 3.''}}}$
${\textstyle B}$: ${\textstyle {\text{''Der blaue Würfel zeigt eine 1 oder eine 6.''}}}$
${\textstyle C}$: ${\textstyle {\text{''Der blaue Würfel zeigt eine kleinere Zahl als der Rote. ''}}}$
${\textstyle D}$: ${\textstyle {\text{''Beide Würfel zeigen die gleiche Zahl.''}}}$
${\textstyle E}$: ${\textstyle {\text{''Keine 4 wird gewürfelt.''}}}$

Aufgabe 1.2

Welche dieser Ereignisse sind stochastisch unabhängig? (Prüfen Sie alle möglichen Kombinationen.) Geben Sie jeweils zunächst eine Vermutung ab und rechnen Sie dann.

Aufgabe 2

Zwei Freunde ${\textstyle A}$ und ${\textstyle B}$ verabreden sich. ${\textstyle A}$ kommt mit Wahrscheinlichkeit ${\textstyle 90\%}$ zum Treffen, ${\textstyle B}$ mit Wahrscheinlichkeit ${\textstyle 80\%}$. Wie groß ist die Wahrscheinlichkeit, dass beide zum Treffen erscheinen?

• Diese Frage kann mit den vorliegenden Informationen nicht beantwortet werden. Wieso nicht?
• Beantworten Sie die Frage, falls man davon ausgehen kann, dass ${\textstyle A}$ und ${\textstyle B}$ unabhängig voneinander zum Treffen erscheinen.

Aufgabe 3

Geben Sie je zwei Beispiele für unabhängige und nicht unabhängige Zufallsvariablen an und zeigen Sie rechnerisch, dass diese (nicht) unabhängig sind. (Geben Sie nicht die Beispiele aus der Vorlesung an!)

Anwendung auf Testverfahren

Führt man ein Test auf eine bestimmte Eigenschaft durch, der möglicherweise falsche Ergebnisse anzeigen kann, so können vier mögliche Kombinationen von Vorliegen der Eigenschaft ${\textstyle E}$ und positivem Testergebnis ${\textstyle T}$ auftreten:
$${\begin{array}{|c|c|c|}\hline ''{\text{richtig positiv}}''&{\text{Test positiv und Eigenschaft liegt auch vor}}&T\cap E\\\hline ''{\text{falsch positiv}}''&{\text{Test positiv,aber Eigenschaft liegt nicht vor}}&T\cap {\overline {E}}\\\hline ''{\text{falsch negativ}}''&{\text{Test negativ, aber Eigenschaft liegt vor}}&{\overline {T}}\cap E\\\hline ''{\text{richtig negativ}}''&{\text{Test negativ und Eigenschaft liegt auch nicht vor}}&{\overline {T}}\cap {\overline {E}}\\\hline \end{array}}$$

Sensitivität

In den meisten Fällen ist davon auszugehen, dass folgende Größen bekannt sind.

• Sensitivität: Wahrscheinlichkeit, ein positives Testergebnis zu erhalten, wenn die Eigenschaft vorliegt: $$P(T|E)={\frac {P(T\cap E)}{P(E)}}={\frac {P({\text{'' richtig positiv ''}})}{P({\text{'' richtig positiv ''}})+P({\text{'' falsch negativ ''}})}}$$

Spezifität

• Spezifität: Wahrscheinlichkeit, ein negatives Testergebnis zu erhalten, wenn die Eigenschaft nicht vorliegt: $$P\left({\overline {T}}|{\overline {E}}\right)={\frac {P({\overline {T}}\cap {\overline {E}})}{P({\overline {E}})}}={\frac {P({\text{'' richtig negativ ''}})}{P({\text{'' richtig negativ ''}})+P({\text{'' falsch positiv ''}})}}$$

Prävalenz

• Prävalenz: Wahrscheinlichkeit, dass die Eigenschaft vorliegt (vor dem Test): $$P(E)=P({\text{'' richtig positiv ''}})+P({\text{'' falsch negativ ''}})$$

Bedingte Wahrscheinlichkeit

Gesucht ist dann die Wahrscheinlichkeit, dass die Eigenschaft tatsächlich vorliegt, wenn ein positives Testergebnis angezeigt wurde, also: $$P(E|T)={\frac {P(T\cap E)}{P(T)}}={\frac {P({\text{'' richtig positiv ''}})}{P({\text{'' richtig positiv ''}})+P({\text{'' falsch positiv ''}})}}$$

Bestimmung der bedingten Wahrscheinlichkeit

Dies lässt sich wie folgt lösen:

1. Es ist:

   ${\textstyle \quad P(T)=P(T\cap E)+P\left(T\cap {\overline {E}}\right)=P\left(E\right)\cdot P\left(T|E\right)+\underbrace {P\left({\overline {E}}\right)} _{=1-P(E)}\cdot \underbrace {P\left(T|{\overline {E}}\right)} _{=1-P\left({\overline {T}}|{\overline {E}}\right)}}$

2. Es ist ${\textstyle \quad P(E|T)={\frac {P(T\cap E)}{P(T)}}={\frac {P\left(E\right)\cdot P\left(T|E\right)}{P\left(E\right)\cdot P\left(T|E\right)\ +\ \left(1-P(E)\right)\cdot \left(1-P\left({\overline {T}}|{\overline {E}}\right)\right)}}}$

Beispiel 1.1

Ein Test auf eine Krankheit liefert in 99 % der Fälle ein richtiges Ergebnis. (d.h. Sensitivität ${\textstyle P(T|E)=0.99}$ und Spezifität ${\textstyle P\left({\overline {T}}|{\overline {E}}\right)=0.99}$) Eine Person wird positiv getestet. Wie groß ist die Wahrscheinlichkeit, dass die Person tatsächlich krank ist?

• Ohne den Wert der Prävalenz lässt sich diese Frage nicht beantworten.

Beispiel 1.2

• Angenommen es gibt (außer dem Testergebnis) keine Anzeichen auf das Vorliegen der Krankheit und in der entsprechenden Bevölkerungsgruppe haben ${\textstyle 0.01}$ % aller Personen die Krankheit. Dann ist die Prävalenz ${\textstyle P(E)=0.0001}$. Also:
  $${\begin{aligned}P(E|T)=0.009804\end{aligned}}$$
  die Wahrscheinlichkeit für das Vorliegen der Krankheit.

Beispiel 1.3

• Angenommen man führt nun einen zweiten Test durch. Dieser ist ebenfalls positiv. Durch den ersten Test hat sich die Prävalenz nun auf ${\textstyle P(E)=0.009803922}$ erhöht. Also: $${\begin{aligned}P(E|T)=0.495002\end{aligned}}$$
  die Wahrscheinlichkeit für das Vorliegen der Krankheit.

• Wir betrachten nun wieder die Situation eines einzelnen positiven Tests. Da es aber zusätzliche Hinweise auf die Krankheit gibt, wird die Prävalenz auf ${\textstyle 0.4}$ geschätzt. Nach dem positiven Test ist nun
  $${\begin{aligned}P(E|T)=0.98507\end{aligned}}$$
  die Wahrscheinlichkeit für das Vorliegen der Krankheit.

Beispiel 1.4

Bei einem anderen Test kennt man die Sensitivität ${\textstyle P(T|E)=0.9}$ und die Spezifität ${\textstyle P\left({\overline {T}}|{\overline {E}}\right)=0.95}$.
Ist ${\textstyle p=P(E)\in [0,1]}$ die Prävalenz, so ist nach einem positiven Test
$$P(E|T)={\frac {p\cdot 0.9}{p\cdot 0.9\ +\ (1-p)\cdot 0.05}}={\frac {0.9p}{0.85p+0.05}}$$
die Wahrscheinlichkeit für das Vorliegen der Eigenschaft.

Beispiel 1.5

Aufgabe

Ein Test hat Sensitivität ${\textstyle 0.98}$ und Spezifität ${\textstyle 0.96}$. Berechnen Sie die Wahrscheinlichkeit, dass bei Vorliegen eines positiven Testergebnisses die untersuchte Eigenschaft tatsächlich vorliegt, wenn die Prävalenz
$${\text{(i)}}\quad p=0.0001\quad \quad {\text{(ii)}}\quad p=0.02\quad \quad {\text{(iii)}}\quad p=0.5$$
beträgt.

Produktregel und Baumdiagramme

Produktregel der Kombinatorik

Die Wahrscheinlichkeit eines Durchschnitts von Ereignissen kann mit Hilfe bedingter Wahrscheinlichkeiten durch die folgende Produktregel der Kombinatorik berechnet werden. Es gilt:
Ist ${\textstyle (\Omega ,P)}$ ein W-Raum und sind ${\textstyle A_{1},\ldots ,A_{n}\in {\mathcal {P}}}$, so gilt $$P(A_{1}\cap \ldots \cap A_{n})=P(A_{1})\cdot P(A_{2}|A_{1})\cdot P\left(A_{3}|(A_{1}\cap A_{2})\right)\cdot \ldots \cdot P\left(A_{n}|(A_{1}\cap \ldots \cap A_{n-1})\right)$$

Baumdiagramm

Darauf basierend kann man mehrstufige ZE mit Hilfe eines Baumdiagramms beschreiben. Dabei gehen zunächst von einem Startknoten Pfade aus, die zu disjunkten Ereignissen ${\textstyle A_{1},\ldots ,A_{n}}$ zugeordneten Knoten führen. Die Pfade werden mit den Wahrscheinlichkeiten ${\textstyle P(A_{1}),\ldots ,P(A_{n})}$ versehen. Von einem ${\textstyle A}$ zugeordneten Knoten können dann immer wieder Pfade zu den Ereignissen ${\textstyle A\cap B_{1},\ldots ,A\cap B_{m}}$ zugeordneten Knoten führen (dabei müssen ${\textstyle A\cap B_{1},\ldots ,A\cap B_{m}}$ wiederum disjunkte Ereignisse sein), die mit den Wahrscheinlichkeiten ${\textstyle P(B_{1}|A),\ldots ,P(B_{m}|A)}$ versehen sind. Die Endkoten (von denen keine Pfade mehr ausgehen) heißen Blätter. Die den Blättern zugeordneten Ereignisse sind dann wiederum disjunkt.

Pfad-Multiplikations- und Pfad-Additionsregel

Es gilt nun:

• Pfad-Multiplikationsregel: Die Wahrscheinlichkeit eines einem Blatt zugeordneten Ereignisses ist das Produkt der Wahrscheinlichkeiten aller Pfade, die zum Blatt führen.
• Pfad-Additionsregel: Die Wahrscheinlichkeit eines durch mehrere Blätter gegebenen Ereignisses ist die Summe der Wahrscheinlichkeiten dieser Blätter.

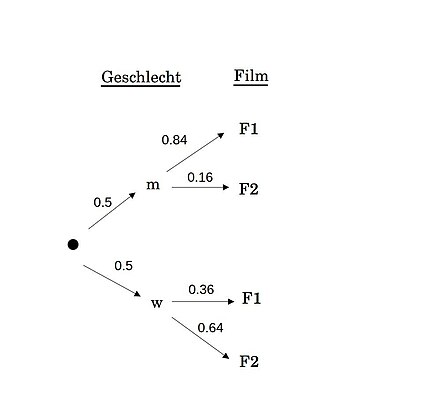
Beispiel 1.1

In einem Kino werden zwei Filme ${\textstyle F1}$ und ${\textstyle F2}$ gezeigt. Bei Film ${\textstyle F1}$ sind ${\textstyle 70\%}$ der Zuschauer männlich, bei Film ${\textstyle F2}$ sind hingegen ${\textstyle 80\%}$ der Zuschauer weiblich. Insgesamt schauen ${\textstyle 60\%}$ aller Zuschauer den Film ${\textstyle F1}$. Gegeben ist also:
$${\begin{aligned}P({\text{m}}|F1)=0.7&&\left(\rightarrow \ P({\text{w}}|F1)=0.3\right)\\P({\text{w}}|F2)=0.8&&\left(\rightarrow \ P({\text{m}}|F2)=0.2\right)\\P(F1)=0.4&&\left(\rightarrow \ P(F2)=0.6\right)\end{aligned}}$$

Beispiel 1.2

Dies ergibt folgendes Baumdiagramm:

Beispiel 1.3

Wir berechnen daraus:
$$P({\text{m}})=0.5\quad {\text{und}}\quad P({\text{w}})=0.5$$
sowie
$${\begin{aligned}P(F1|{\text{m}})=0.84&\quad {\text{und}}\quad &P(F2|{\text{m}})=0.16\\P(F1|{\text{w}})=0.36&\quad {\text{und}}\quad &P(F2|{\text{w}})=0.64\end{aligned}}$$

Beispiel 1.4

Nun lässt sich auch das umgekehrte Baumdiagramm erstellen:

Beispiel 2.1

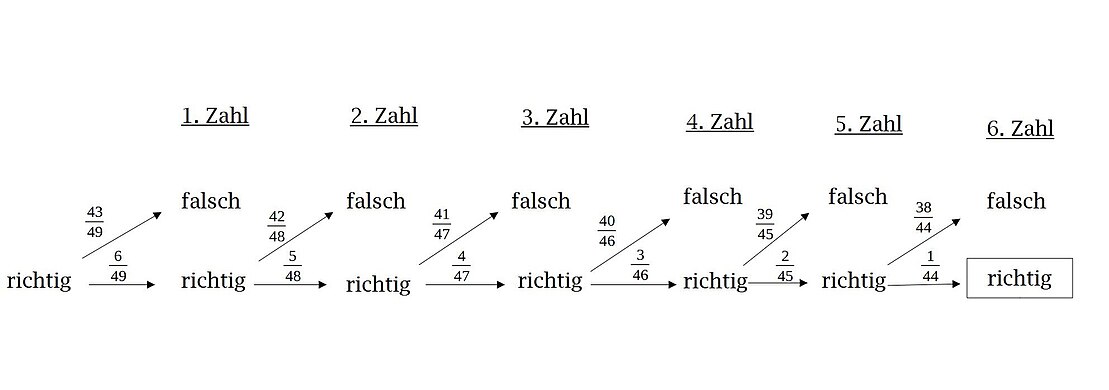
Nochmals Zahlenlotto: Die Wahrscheinlichkeit für einen Gewinn (${\textstyle G}$: Richtige) lässt sich wie folgt bestimmen: Bezeichne ${\textstyle B_{i}}$ das Ereignis: "Die ${\textstyle i}$-te gezogene Zahl ist unter den vom Spieler gewählten Zahlen." (für ${\textstyle i=1,\ldots ,6}$)
Dann gilt:

$$P(B_{1})={\frac {6}{49}},\quad P(B_{2}|B_{1})={\frac {5}{48}},\quad P(B_{3}|B_{1}\cap B_{2})={\frac {4}{47}}$$

$$P(B_{4}|B_{1}\cap B_{2}\cap B_{3})={\frac {3}{46}},$$ $$P(B_{5}|B_{1}\cap \ldots \cap B_{4})={\frac {2}{45}},\quad P(B_{6}|B_{1}\cap \ldots \cap B_{5})={\frac {1}{44}}$$

Es ist ${\textstyle G=B_{1}\cap \ldots \cap B_{6}}$ und folglich
$${\begin{aligned}P(G)={\frac {1}{13983816}}\end{aligned}}$$

Beispiel 2.2

Das Baumdiagramm sieht dabei wie folgt aus:

Beispiel 2.3

Der Fall, in dem ${\textstyle G}$ eintritt, ist eingerahmt. Mit der Pfad-Multiplikationsregel ergibt sich das Ergebnis von oben.

Beispiel 3.1

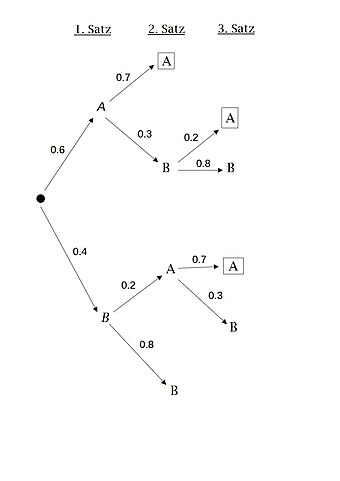
Zwei Spieler ${\textstyle A}$ und ${\textstyle B}$ tragen ein Tennismatch über zwei Gewinnsätze aus. Den ersten Satz gewinnt ${\textstyle A}$ mit einer Wahrscheinlichkeit von ${\textstyle 0.6}$. Falls ${\textstyle A}$ einen Satz gewonnen hat, gewinnt er den nächsten mit einer Wahrscheinlichkeit von ${\textstyle 0.7}$, hat er jedoch einen Satz verloren, gewinnt er den nächsten nur noch mit einer Wahrscheinlichkeit von ${\textstyle 0.2}$. Gesucht ist die Wahrscheinlichkeit, dass ${\textstyle A}$ das Match gewinnt:

Beispiel 3.2

Beispiel 3.3

Die Fälle, bei denen ${\textstyle A}$ das Match gewinnt, sind eingerahmt. Es ergibt sich
$$P\left({\text{''}}A{\text{ gewinnt''}}\right)=\ 0.6\cdot 0.7\ +\ 0.6\cdot 0.3\cdot 0.2\ +\ 0.4\cdot 0.2\cdot 0.7\ =0.512$$

Aufgabe 1

Die Buchstaben ${\textstyle I,I,I,I,M,P,P,S,S,S,S}$ werden zufällig aneinandergereiht. Wie groß ist die Wahrscheinlichkeit, dabei das Wort MISSISSIPPI zu erhalten? Beantworten Sie die Fragen mit Hilfe eines Baumdiagramms.

Aufgabe 2

Erstellen Sie zu den Beispielen in Bedingte Wahrscheinlichkeiten jeweils ein Baumdiagramm.

Aufgabe 3

Einer Schulstatistik eines Gymnasiums, in dem sich jeder Schüler für genau eines der Leistungsfächer Mathematik und Deutsch sowie für eines der Grundkursfächer Englisch und Französisch zu entscheiden hat, ist zu entnehmen, dass 40% Mathematik gewählt haben. Für Französisch entscheiden sich 60% der Deutsch- und 50% der Mathematikleistungskursschüler. Erstellen Sie dazu das entsprechende Baumdiagramm sowie das umgekehrte Baumdiagramm.

Satz von Bayes und Satz von der totalen Wahrscheinlichkeit

Sei ${\textstyle (\Omega ,P)}$ ein W-Raum. Die folgenden Regeln sind geeignet, um bedingte Wahrscheinlichkeiten miteinander zu verrechnen:

Satz von Bayes (für zwei Ereignisse)

Für ${\textstyle A,B\in {\mathcal {P}}}$ gilt:
$$P(A|B)={\frac {P(A)\cdot P(B|A)}{P(B)}}$$

Beispiel Satz von Bayes (für zwei Ereignisse)

${\textstyle 30\%}$ aller Erwachsenen sind Raucher, bei den Männern sind es sogar ${\textstyle 34\%}$. Wieviel Prozent aller Raucher sind Männer? $${\begin{aligned}{\text{Gegeben:}}&&P(R)=0.3,\quad P(R|M)=0.34,\quad \underbrace {P(M)=0.5} _{\text{bekannt}}\\\rightarrow &&P(M|R)=0.5667\end{aligned}}$$

Satz von der totalen Wahrscheinlichkeit

Sind ${\textstyle A_{1},\ldots ,A_{n},B\in {\mathcal {P}}}$ und gilt ${\textstyle A_{1}\cup \ldots \cup A_{n}=\Omega }$, so folgt:
$$P(B)=\sum _{i=1}^{n}P(A_{i})\cdot P(B|A_{i})$$

Satz von Bayes (allgemeiner Fall)

Sind ${\textstyle A_{1},\ldots ,A_{n},B\in {\mathcal {P}}}$ und gilt ${\textstyle A_{1}\cup \ldots \cup A_{n}=\Omega }$, so folgt:
$$P(A_{j}|B)={\frac {P(A_{j})\cdot P(B|A_{j})}{\sum \limits _{i=1}^{n}P(A_{i})\cdot P(B|A_{i})}}\quad (j=1,\ldots ,n)$$

Beispiel 1.1

Vier Maschinen produzieren den gleichen Artikel. Sie haben unterschiedliche Produktionsanteile und unterschiedliche Ausschussquoten. Im einzelnen gilt:
$${\begin{array}{|c|c|c|c|c|}\hline {\text{Maschine}}&1&2&3&4\\\hline {\text{Produktionsanteil}}&10\;\%&20\;\%&30\;\%&40\;\%\\\hline {\text{Ausschussquote}}&3\;\%&9\;\%&7\;\%&2\;\%\\\hline \end{array}}$$

Wir betrachten die Ereignisse
$M_{1},\ldots ,M_{4}:$ " Von Maschine $1,\ldots ,4$ produziert. "
und
A : " Ausschuss " .
Oben sind die Werte ${\textstyle P(M_{i})}$ und ${\textstyle P(A|M_{i})\ ({\text{für}}\ i=1,\ldots ,4)}$ gegeben.

Beispiel 1.2

Damit ${\textstyle P(A)=0.05}$
Ebenso berechnet sich:
${\textstyle P({\overline {A}})=0.95}$
Nun ergibt sich daraus:
${\textstyle {\begin{aligned}P(M_{1}|A)=0.06\\&&\\P(M_{2}|A)=0.36\\&&\\P(M_{3}|A)=0.42\\&&\\P(M_{4}|A)=0.16\end{aligned}}}$
Die zum Ausschuss gehörenden Bauteile wurden also zu ${\textstyle 6,36,42,16\ \%}$ von den Maschinen ${\textstyle 1,2,3,4}$ produziert.

Beispiel 1.3

Analog ist:
${\textstyle {\begin{aligned}P(M_{1}|{\overline {A}})=0.1021\\&&\\P(M_{2}|{\overline {A}})=0.1916\\&&\\P(M_{3}|{\overline {A}})=0.2937\\&&\\P(M_{4}|{\overline {A}})=0.4126\end{aligned}}}$
Die nicht zum Ausschuss gehörenden Bauteile wurden also zu ${\textstyle 10.21,\ 19.16,\ 29.37,\ 41.26\ \%}$ von den Maschinen ${\textstyle 1,2,3,4}$ produziert.

Aufgabe 1

Insgesamt kommen ${\textstyle 80\%}$ aller Hörer einer Vorlesung pünktlich, unter denjenigen, die mit dem Auto kommen sind es sogar ${\textstyle 95\%}$. Zusätzlich sei bekannt, dass insgesamt ${\textstyle 30\%}$ der Hörer mit dem Auto kommen. Wie groß ist der Anteil der Autofahrer

• unter den Pünktlichen?
• unter denjenigen, die zu spät kommen?

Aufgabe 2

Bei einer Telefonberatung arbeiten ${\textstyle 5}$ verschiedene Berater ${\textstyle B_{1},\ldots ,B_{5}}$. Sie bearbeiten unterschiedliche Anteile der Anfragen und haben verschiedene Quoten bezüglich der Zufriedenheit der Kunden:

$${\begin{array}{|c|c|c|c|c|c|}\hline {\text{Berater}}&B_{1}&B_{3}&B_{3}&B_{4}&B_{5}\\\hline {\text{bearbeitet den folgenden Anteil der Anfragen}}&0.15&0.2&0.2&0.4&0.05\\\hline {\text{Anteil der zufriedenen Kunden bei diesem Berater}}&0.2&0.8&0.4&0.7&0.9\\\hline \end{array}}$$

• Wie hoch ist der Anteil der zufriedenen Kunden insgesamt?
• Berechnen Sie den Anteile der verschiedenen Beratern unter den zufreidenen Kunden bzw. unter den unzufriedenen Kunden.

Aufgabe 3

Bei einem Glücksspiel befinden sich ${\textstyle 20}$ schwarze Kugeln in einer Lostrommel. Der Spieler darf zunächst ${\textstyle 2}$ Würfel werfen und dann soviele weiße Kugeln dazumischen, wie die Augensumme beträgt. Dann darf er aus den gemischten Kugeln eine ziehen. Ist die gezogene Kugel weiß, hat er gewonnen.

• Wie hoch ist die Gewinnchance des Spielers?
• Berechnen Sie für alle Werte ${\textstyle k=2,\ldots ,12}$ die Wahrscheinlichkeit, dass ein Spieler, der gerade gewonnen hat, die Augensumme ${\textstyle k}$ gewürfelt hat.

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Bedingte%20Wahrscheinlichkeiten
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.