Kurs:Statistik für Anwender/Gleichverteilte Zufallsvariablen

Gleichverteilte ZV

Seien ${\textstyle a,b\in \mathbb {R} }$ mit ${\textstyle a<b}$ gegeben.

Definition gleichverteilte Zufallsvariable

Eine ZV ${\textstyle X}$ mit der W-Dichte ${\textstyle \quad f:\mathbb {R} \to [0,\infty ),\ f(t)=\left\{{\begin{array}{ccl}{\frac {1}{b-a}}&,&{\text{falls}}\ t\in [a,b]\\0&,&{\text{sonst}}\end{array}}\right.}$
heißt gleichverteilt auf dem Intervall ${\textstyle [a,b]}$ .

Verteilungsfunktion gleichverteilte Zufallsvariable

Für die Verteilungsfunktion ${\textstyle F}$ von ${\textstyle X}$ gilt dann: $F(x)=\int \limits _{-\infty }^{x}f(t)dt=\left\{{\begin{array}{ccl}0&,&{\text{falls}}\ x\in ]-\infty ,a[\\{\frac {x-a}{b-a}}&,&{\text{falls}}\ x\in [a,b]\\1&,&{\text{falls}}\ x\in ]b,\infty [\end{array}}\right.$

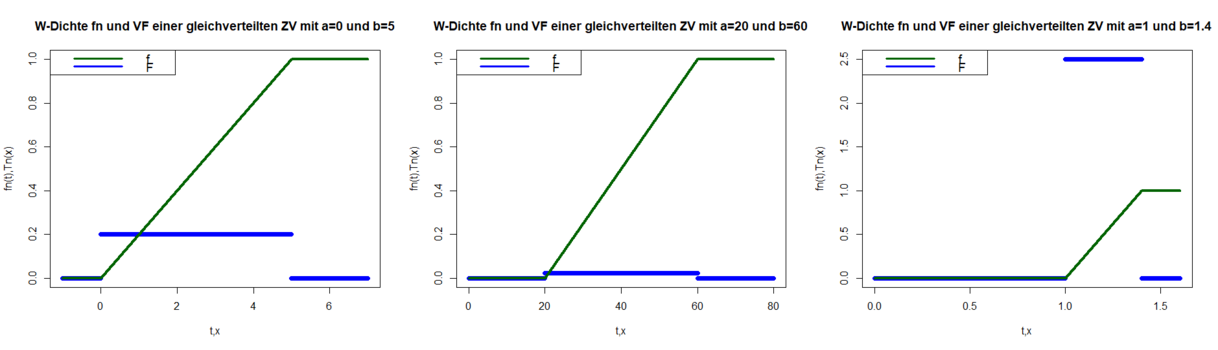
Beispiel gleichverteilte Zufallsvariable

Beispiel gleichverteilte Zufallsvariable interaktiv

Interaktive Shiny-App zur Gleichverteilung:
Download und Link

Wahrscheinlichkeit gleichverteilte Zufallsvariable

Für eine auf dem Intervall ${\textstyle [a,b]}$ gleichverteilte ZV ${\textstyle X}$ gilt: ${\textstyle \quad P(a\leq X\leq b)=1}$
Weiterhin gilt für beliebige Zahlen ${\textstyle u,v\in \mathbb {R} }$ mit ${\textstyle a\leq u\leq v\leq b}$ :
$\quad P(u\leq X\leq v)={\frac {v-u}{b-a}}$
Die Gleichverteilung kann also als Modell verwendet werden, wenn ${\textstyle Z}$ nur Werte in ${\textstyle [a,b]}$ annehmen kann und mit gleicher Wahrscheinlichkeit in alle gleich großen Teilbereiche fällt.

Erwartungswert und Varianz gleichverteilte Zufallsvariable

Für eine auf dem Intervall ${\textstyle [a,b]}$ gleichverteilte ZV ${\textstyle X}$ gilt: $E(X)={\frac {a+b}{2}}\quad {\text{und}}\quad V(X)={\frac {(b-a)^{2}}{12}}$

Praktische Anwendung gleichverteilte Zufallsvariable

In bestimmten Situationen ist es naheliegend, gleichverteilte ZV als Modell zu verwenden:

Eine ZV, die den Winkel (im Bogenmaß bzw. im Gradmaß) beschreibt, den der Zeiger eines Glücksrad mit einer festen Markierung einschließt, kann plausibel durch eine Gleichverteilung (auf ${\textstyle [0,2\pi ]}$ bzw. auf ${\textstyle [0,360]}$ ) beschrieben werden.
In einer Stadt fährt eine U-Bahn alle 5 Minuten. Die Wartezeit auf die Bahn (in Minuten) bei zufälligem Eintreffen am Bahnsteig kann plausibel durch eine auf ${\textstyle [0,5]}$ gleichverteilte ZV beschrieben werden.

Beispiel I

Für eine auf ${\textstyle [0,20]}$ gleichverteilte ZV ${\textstyle Z}$ gilt $P(Z\leq 8)=0.4,\quad P(Z\geq 15)=0.25,$ $P(3\leq Z\leq 16)=0.65,$ $P(-4\leq Z\leq 22)=1$
Außerdem ist ${\textstyle E(Z)=10}$ und ${\textstyle \sigma _{Z}=5.7735}$ .

Beispiel II

Für eine auf ${\textstyle [-8,8]}$ gleichverteilte ZV gilt: $P(2\leq Z\leq 10)=0.375=P(2\leq Z),$ $P(-12\leq Z\leq -4)=0.25=P(Z\leq -4)$

Außerdem ist ${\textstyle E(Z)=0}$ und ${\textstyle \sigma _{Z}={\frac {16}{\sqrt {12}}}=4.6188}$ .

Gleichverteilte Zufallsvariable in R

Für eine auf dem Intervall ${\textstyle [a,b]}$ -gleichverteilte ZV ${\textstyle X}$ berechnet man in R:

die Funktionswerte der W-Dichte von ${\textstyle X}$ durch: ${\textstyle f(t)=\color {blue}{dunif(t,a,b)}}$
die Funktionswerte der VF von ${\textstyle X}$ durch: ${\textstyle F(x)=\color {blue}{punif(x,a,b)}}$
die Wahrscheinlichkeit für ${\textstyle X\in [u,v]}$ durch: ${\textstyle P(u\leq X\leq v)=\color {blue}{punif(v,a,b)-punif(u,a,b)}}$

Aufgabe I

Seien ${\textstyle a}$ , ${\textstyle b\in \mathbb {R} }$ mit ${\textstyle a<b}$ . Betrachten Sie die Funktion $f\colon \mathbb {R} \to \mathbb {R} ,{\text{ mit }}f(t)={\begin{cases}{\frac {1}{b-a}},{\text{ falls }}t\in \left[a,b\right],\\0,{\text{ sonst}}\end{cases}}$

Skizzieren Sie den Graphen von ${\textstyle f}$ für verschiedene Werte von ${\textstyle a}$ und ${\textstyle b}$ (evtl. auch mit R).
Zeigen Sie, dass ${\textstyle f}$ eine W-Dichte ist.
Überlegen Sie Beispiele für Zufallsexperimente, die durch eine ZV mit der W-Dichte ${\textstyle f}$ beschrieben werden können.
Wie sieht die Verteilungsfunktion einer solchen ZV ${\textstyle X}$ aus? Geben Sie die Funktionsvorschrift an und skizzieren Sie die Funktion.
Sei ${\textstyle X}$ eine stetige ZV mit der W-Dichte ${\textstyle f}$ für ${\textstyle a=0}$ und ${\textstyle b=10}$ . Berechnen Sie die Wahrscheinlichkeiten ${\textstyle P(1\leq X\leq 4)}$ , ${\textstyle P(4<X\leq 12)}$ , ${\textstyle P(X<2)}$ , ${\textstyle P(X\geq 0)}$ und ${\textstyle P(X>10)}$ .