Zusammenhang Fläche unter Graph und Integral
[Bearbeiten]Ist  eine (stückweise stetige) Funktion, so kann die Fläche
eine (stückweise stetige) Funktion, so kann die Fläche ![{\textstyle F_{[a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c88c4933bb89f6d9eaaa68f9422b3b8e5f14982f) über einem Intervall
über einem Intervall ![{\textstyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c780cbaafb5b1d4a6912aa65d2b0b1982097108) unter dem Graphen von
unter dem Graphen von  mit einem Integral berechnet werden:
mit einem Integral berechnet werden: ![{\displaystyle F_{[a,b]}=\int \limits _{a}^{b}f(t)dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fe6443ba3bf78771e3d5046ccdff34f24ffb449)
Hauptsatzes der Differential- und Integralrechnung
[Bearbeiten]Normalerweise berechnet man Integrale mit Hilfe des Hauptsatzes der Differential- und Integralrechnung. Er besagt:
Falls  eine Stammfunktion von
eine Stammfunktion von  ist (d.h.
ist (d.h.  für
für  ), so gilt
), so gilt ![{\displaystyle \int \limits _{a}^{b}f(t)dt=\left[F(t)\right]_{a}^{b}=F(b)-F(a).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b24ecc60695212bf25adedcc60c5f0d0851ce873)
Ist  (konstante Funktion), so ist
(konstante Funktion), so ist  eine Stammfunktion von
eine Stammfunktion von  .
.
Also:

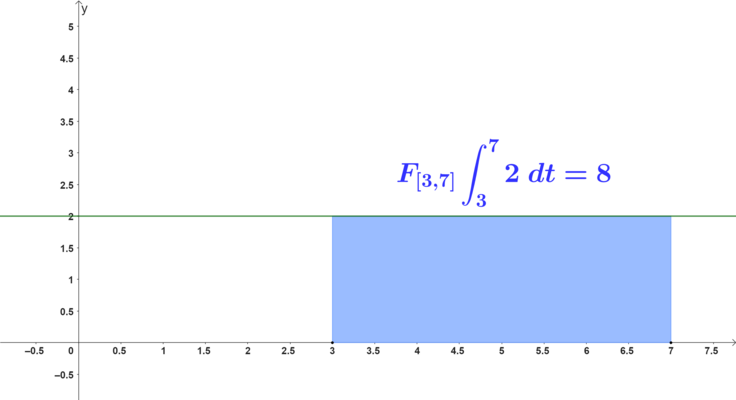
Anmerkung: Fläche hätte auch als Rechtecksfläche berechnet werden können.
Ist  , so ist
, so ist  eine Stammfunktion von
eine Stammfunktion von  .
.
Also:

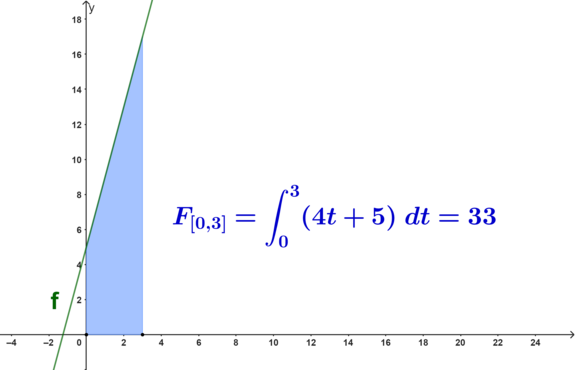
Anmerkung: Fläche hätte auch als Summe von Rechtecks- und Dreiecksfläche berechnet werden können.
Ist  , so ist
, so ist  eine Stammfunktion von
eine Stammfunktion von  .
.
Also:


Ist  , so ist
, so ist  eine Stammfunktion von
eine Stammfunktion von  .
.
Also:

![{\textstyle =\left[8\cdot \exp \left({\frac {t}{4}}\right)\right]_{-4}^{12}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74a0293764081d096cf9a0fd6b4a8ef0644c09da)


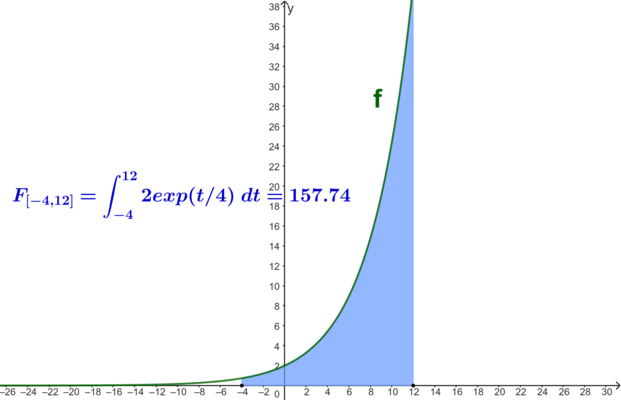
Bei der Berechnung von Integralen gelten die folgende Regeln:

 (für
(für  )
) (falls
(falls  )
)
Beispiel Anwendung Regeln für Integrale I
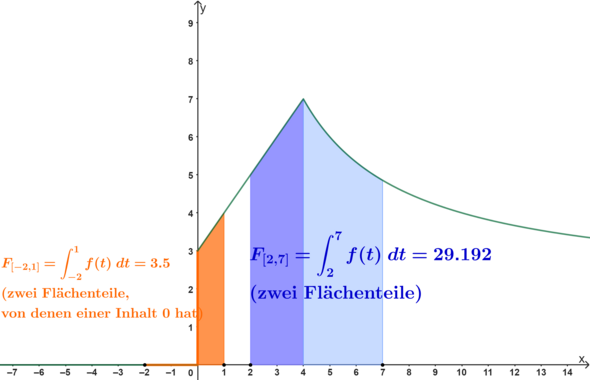
[Bearbeiten]Die letzte Regel ist vor allem dann wichtig, wenn Funktionen abschnittsweise definiert sind.
Für

ist
![{\displaystyle \int \limits _{-2}^{1}f(t)dt=\int \limits _{-2}^{0}0\ dt+\int \limits _{0}^{1}(t+3)dt=[0]_{-2}^{0}+\left[{\frac {1}{2}}t^{2}+3t\right]_{0}^{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/152ce27c81e852640257a5467b65b4c7e9e81176)

Beispiel Anwendung Regeln für Integrale II
[Bearbeiten]und

![{\displaystyle =\left[{\frac {1}{2}}t^{2}+3t\right]_{2}^{4}+\left[2t+20\ln(t)\right]_{4}^{7}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/584a04526f8814ed619477376e4fe8b134014807)



Beispiel Anwendung Regeln für Integrale III
[Bearbeiten]Die Bestimmung einer Stammfunktion ist nicht immer einfach. Für viele Funktionen sind jedoch Stammfuntkionen bekannt. Außerdem gibt es einige weitere Methoden zur Bestimmung von Stammfunktionen bzw. zur Berechnung von Integralen (z.B. partielle Integration, Substitution). Wir wollen jedoch im Rahmen dieser Vorlesung nicht näher darauf eingehen.
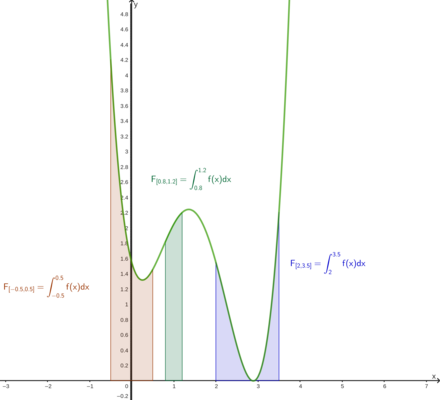
Berechnen Sie die folgenden Integrale. Skizzieren (oder plotten) Sie jeweils auch den Graphen der integrierten Funktion und zeichnen Sie die Fläche ein, die durch das Integral berechnet wird:



Für unsere Zwecke sind auch sogenannte uneigentliche Integrale von Bedeutung. Dabei handelt es sich um Integrale, bei denen die untere Grenze  oder die obere Grenze
oder die obere Grenze  ist (oder beides). Man berechnet solche Integrale mit Hilfe von Grenzwerten.
ist (oder beides). Man berechnet solche Integrale mit Hilfe von Grenzwerten.
Ist  eine Funktion mit Stammfunktion
eine Funktion mit Stammfunktion  , so ist:
, so ist: ![{\displaystyle {\begin{array}{ccccccc}\int \limits _{a}^{\infty }f(t)dt&=&\left[F(t)\right]_{a}^{\infty }&=&\lim \limits _{t\to \infty }F(t)&-&F(a)\\\int \limits _{-\infty }^{b}f(t)dt&=&\left[F(t)\right]_{-\infty }^{b}&=&F(b)&-&\lim \limits _{t\to -\infty }F(t)\\\int \limits _{-\infty }^{\infty }f(t)dt&=&\left[F(t)\right]_{-\infty }^{\infty }&=&\lim \limits _{t\to \infty }F(t)&-&\lim \limits _{t\to -\infty }F(t)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/611ea11ffd0923679dc96af4bfdfc146bdb9b016)
Man spricht auch dann von einem ’uneigentlichen Integral’, wenn die integrierte Funktion  eine Defintionslücke hat und diese im Integrationsbereich
eine Defintionslücke hat und diese im Integrationsbereich ![{\textstyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c780cbaafb5b1d4a6912aa65d2b0b1982097108) liegt. Wir behandeln diesen Fall aber im Rahmen dieser Vorlesung nicht.
liegt. Wir behandeln diesen Fall aber im Rahmen dieser Vorlesung nicht.
Für
 ist:
ist:![{\textstyle \int \limits _{2}^{\infty }f(t)dt=\left[-{\frac {6}{t}}\right]_{2}^{\infty }=\lim \limits _{t\to \infty }\left(-{\frac {6}{t}}\right)-\left(-{\frac {6}{2}}\right)=0-\left(-3\right)=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9156e7e1afc3bd36d6d0be00ac127fd9ec768d1d)
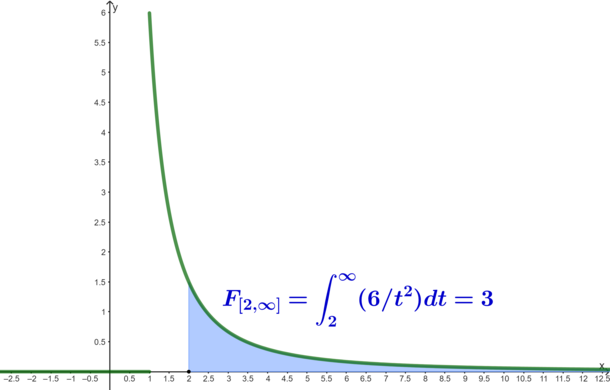
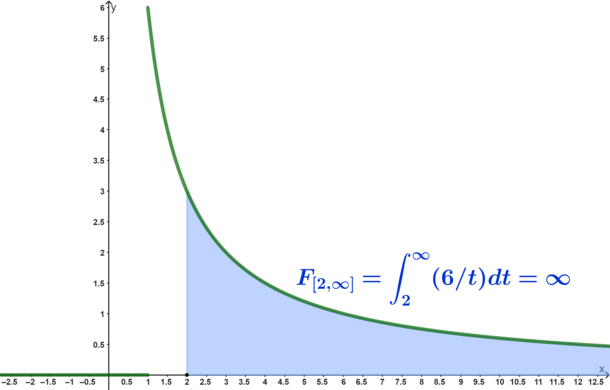
Für
 ist:
ist:![{\textstyle \int \limits _{2}^{\infty }f(t)dt=\left[6\ln(t)\right]_{2}^{\infty }=\lim \limits _{t\to \infty }\left(6\ln(t)\right)-6\ln(2)=\infty -6\ln(2)=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/166378100403b6fbdcc6b77969db22a68cf4a4d7)
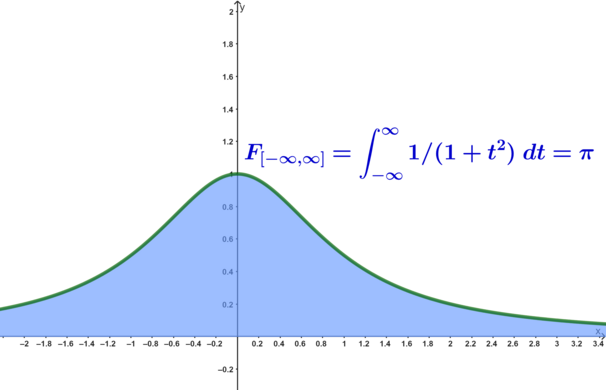
Für  ist
ist
![{\textstyle \int \limits _{-\infty }^{\infty }f(t)dt=\left[\arctan(t)\right]_{-\infty }^{\infty }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3063f154af3c3f1811b06452a8ca525b1d5ea49)

(Wir begründen an dieser Stelle nicht, dass  eine Stammfunktion von
eine Stammfunktion von  ist.)
ist.)
Berechnen Sie die folgenden uneigentlichen Integrale. Skizzieren (oder plotten) Sie jeweils auch den Graphen der integrierten Funktion und zeichnen Sie die Fläche ein, die durch das Integral berechnet wird:
 und
und  für
für 
 und
und 
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.


![{\textstyle F_{[a,b]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c88c4933bb89f6d9eaaa68f9422b3b8e5f14982f)
![{\textstyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c780cbaafb5b1d4a6912aa65d2b0b1982097108)

![{\displaystyle F_{[a,b]}=\int \limits _{a}^{b}f(t)dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fe6443ba3bf78771e3d5046ccdff34f24ffb449)



![{\displaystyle \int \limits _{a}^{b}f(t)dt=\left[F(t)\right]_{a}^{b}=F(b)-F(a).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b24ecc60695212bf25adedcc60c5f0d0851ce873)















![{\textstyle =\left[8\cdot \exp \left({\frac {t}{4}}\right)\right]_{-4}^{12}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74a0293764081d096cf9a0fd6b4a8ef0644c09da)









![{\displaystyle \int \limits _{-2}^{1}f(t)dt=\int \limits _{-2}^{0}0\ dt+\int \limits _{0}^{1}(t+3)dt=[0]_{-2}^{0}+\left[{\frac {1}{2}}t^{2}+3t\right]_{0}^{1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/152ce27c81e852640257a5467b65b4c7e9e81176)


![{\displaystyle =\left[{\frac {1}{2}}t^{2}+3t\right]_{2}^{4}+\left[2t+20\ln(t)\right]_{4}^{7}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/584a04526f8814ed619477376e4fe8b134014807)








![{\displaystyle {\begin{array}{ccccccc}\int \limits _{a}^{\infty }f(t)dt&=&\left[F(t)\right]_{a}^{\infty }&=&\lim \limits _{t\to \infty }F(t)&-&F(a)\\\int \limits _{-\infty }^{b}f(t)dt&=&\left[F(t)\right]_{-\infty }^{b}&=&F(b)&-&\lim \limits _{t\to -\infty }F(t)\\\int \limits _{-\infty }^{\infty }f(t)dt&=&\left[F(t)\right]_{-\infty }^{\infty }&=&\lim \limits _{t\to \infty }F(t)&-&\lim \limits _{t\to -\infty }F(t)\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/611ea11ffd0923679dc96af4bfdfc146bdb9b016)

![{\textstyle \int \limits _{2}^{\infty }f(t)dt=\left[-{\frac {6}{t}}\right]_{2}^{\infty }=\lim \limits _{t\to \infty }\left(-{\frac {6}{t}}\right)-\left(-{\frac {6}{2}}\right)=0-\left(-3\right)=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9156e7e1afc3bd36d6d0be00ac127fd9ec768d1d)


![{\textstyle \int \limits _{2}^{\infty }f(t)dt=\left[6\ln(t)\right]_{2}^{\infty }=\lim \limits _{t\to \infty }\left(6\ln(t)\right)-6\ln(2)=\infty -6\ln(2)=\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/166378100403b6fbdcc6b77969db22a68cf4a4d7)


![{\textstyle \int \limits _{-\infty }^{\infty }f(t)dt=\left[\arctan(t)\right]_{-\infty }^{\infty }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3063f154af3c3f1811b06452a8ca525b1d5ea49)







