Kurs:Statistik für Anwender/Streumaße

Streumaße

Ein Streumaß eines Merkmals gibt an, wie stark die Beobachtungswerte ’verteilt’ sind. Manche Streumaße berechnen sich aus der Abweichung der Beobachtungswerte vom Mittelwert.

Spannweite

Ist ${\textstyle X:\Omega \to \mathbb {R} }$ ein quantitatives Merkmal mit der Grundgesamtheit ${\textstyle \Omega }$, so nennt man $$S(X)=\max \limits _{\omega \in \Omega }X(\omega )-\min \limits _{\omega \in \Omega }X(\omega )$$
die Spannweite von ${\textstyle X}$.

Beispiel Spannweite

(vergleiche Beispiele Modalwert)

• Beispiel I (Verkehrsmittel): Bildung der Spannweite macht hier keinen Sinn
• Beispiel II (Versuchspflanzen): ${\textstyle S(X)=22}$
• Beispiel III (Daphnien): ${\textstyle S(X)=11}$

Anmerkung zur Spannweite

Die Spannweite hängt nur von den beiden extremen Merkmalsausprägungen ab und nutzt daher nur einen sehr kleinen Teil der vorhandenen Informationen.

Berechnung der Spannweite in R

In R: Man erstellt einen Vektor daten mit den Daten der Urliste und kann dann mit max(daten)-min(daten) die Spannweite berechnen.

p-Quantile

Definition p-Quantile I

Ist ${\textstyle X:\Omega \to A}$ ein mindestens nach einer Ordinalskala verteiltes Merkmal mit dem Merkmalsraum ${\textstyle A}$ und ist ${\textstyle p\in [0,1]}$ eine Zahl, so heißt eine Merkmalsausprägung ${\textstyle a\in A}$ ${\textstyle p}$-Quantil, falls:
$${\frac {\left|\{\omega \in \Omega ;\ X(\omega )<a\}\right|}{n}}\leq p\leq {\frac {\left|\{\omega \in \Omega ;\ X(\omega )\leq a\}\right|}{n}}$$
(Man schreibt ${\textstyle X_{p}}$ für ein ${\textstyle p}$-Quantil des Merkmals ${\textstyle X}$.)

Definition p-Quantile II

• Der Anteil der Beobachtungswerte,die ${\textstyle <X_{p}}$ sind, ist höchstens ${\textstyle p}$.
• Der Anteil der Beobachtungswerte, die ${\textstyle \leq X_{p}}$ sind, ist mindestens ${\textstyle p}$.

Das heißt: Durch die Hinzunahme der einen Merkmalsausprägung ${\textstyle X_{p}}$ (zu denen, die kleiner sind) erreicht oder überschreitet der Anteil der Beobachtungswerte den Wert ${\textstyle p}$. (Der Median ist ein ${\textstyle 0.5}$-Quantil.)

Berechnung p-Quantile

Ist ${\textstyle x_{1}\leq x_{2}\leq \ldots \leq x_{n}}$ die geordnete Datenreihe zu ${\textstyle X}$, so gilt

• Ist ${\textstyle p\cdot n\notin \mathbb {N} }$, so ist ${\textstyle x_{[p\cdot n]+1}}$ das einzige ${\textstyle p}$-Quantil. (Dabei bezeichnet ${\textstyle [r]}$ (zu ${\textstyle r\in \mathbb {R} }$) die größte ganze Zahl, die ${\textstyle \leq r}$ ist.)
• Ist ${\textstyle p\cdot n\in \mathbb {N} }$, so sind ${\textstyle x_{p\cdot n}}$ und ${\textstyle x_{p\cdot n+1}}$ die einzigen ${\textstyle p}$-Quantile. (Für quantitative Merkmale bezeichnet man in diesem Fall oft auch ${\textstyle X_{p}={\frac {x_{p\cdot n}+x_{p\cdot n+1}}{2}}}$ als das ${\textstyle p}$-Quantil.)

Beispiele p-Quantile

(vergleiche Beispiele Modalwert)

Beispiel Versuchspflanzen I

Bei einer Gruppe von Versuchspflanzen der selben Art wird das Wachstum der Sprossachse (in cm) gemessen, man erhält folgende Urliste:
${\textstyle 110,124,120,118,111,124,128,115,119,122,106,114,108,117,124,117,115,}$
${\textstyle 109,114,114,123,112,116}$
Bei 23 Werten ist

• das ${\textstyle 0.3}$-Quantil der ${\textstyle \underbrace {\left([0.3\cdot 23]+1\right)} _{=7}}$-te, Beobachtungswert, also ${\textstyle X_{0.3}=114}$
• das ${\textstyle 0.6}$-Quantil der ${\textstyle \underbrace {\left([0.6\cdot 23]+1\right)} _{=14}}$-te, Beobachtungswert, also ${\textstyle X_{0.6}=117}$

Beispiel Versuchspflanzen II

• das ${\textstyle 0.99}$-Quantil der ${\textstyle \underbrace {\left([0.99\cdot 23]+1\right)} _{=23}}$-te, Beobachtungswert, also ${\textstyle X_{0.99}=128}$

Beispiel Daphnien

Bei 50 Daphnien wird die Anzahl der Nachkommen erhoben. Man erhält die folgenden absoluten Häufigkeiten:

$${\begin{array}{|c||c|c|c|c|c|c|c|c|c|}\hline {\text{Zahl der Nachkommen }}a&0&1&2&3&4&5&8&11\\\hline {\text{absolute Häufigkeit }}h(a)&10&13&11&7&5&2&1&1\\\hline \end{array}}$$

Bei 50 Werten ist $$X_{0.2}=0.5,\quad X_{0.3}=1,\quad X_{0.9}=4.5$$

Berechnung p-Quantile in R

In R: Man erstellt einen Vektor daten mit den Daten der Urliste und kann dann mit quantile(daten,${\textstyle p}$,type=2) das ${\textstyle p}$-Quantil berechnen.

Quartil und Perzentil

Man nennt die Quantile ${\textstyle X_{0.25},\ X_{0.5},\ X_{0.75}}$ auch 1., 2. und 3. Quartil von ${\textstyle X}$. Zusätzlich bezeichnet man die Extremwerte ${\textstyle \min \limits _{\omega \in \Omega }X(\omega )}$ und ${\textstyle \max \limits _{\omega \in \Omega }X(\omega )}$ als 0. und 4. Quartil von ${\textstyle X}$. Außerdem bezeichnet man ein (das) ${\textstyle {\frac {i}{100}}}$-Quantil (für ${\textstyle i=0,\ldots ,100}$) auch als ${\textstyle i}$-tes Perzentil. Für quantitative Merkmale bezeichnet man die Differenz ${\textstyle X_{1-p}-X_{p}}$ ${\textstyle \left({\text{für}}\ p\in \left[0,{\frac {1}{2}}\right]\right)}$ als ${\textstyle p}$-Quantilsabstand, insbesondere heißt ${\textstyle X_{0.75}-X_{0.25}}$ Quartilsabstand.

Boxplots

Mit Hilfe der Quantile lassen sich verschiedene informative grafische Darstellungen für Merkmale erstellen, die insbesondere zum Vergleich von Merkmalen gut geeignet sind. Eine verbreitetes Beispiel dafür sind die sogenannten Boxplots, die in verschiedenen Varianten auftreten.

Erstellung von Boxplots I

Für ein quantitativ verteiltes Merkmal ${\textstyle X:\Omega \to \mathbb {R} }$ geht man dabei beispielsweise wie folgt vor:

• Die Skala nach der das Merkmal ${\textstyle X}$ verteilt ist, wird eingezeichnet.
• Eine Box wird eingetragen, die vom 1. bis zum 3.Quartil reicht. Auf Höhe des 2. Quartils wird die Box durch einen Trennstrich in 2 Teile geteilt. (Variante: Der Trennstrich wird auf Höhe des arithmetischen Mittelwerts eingetragen.)

Erstellung von Boxplots II

• An beiden Enden der Box werden die sogenannten Whiskers (Fühler, Antennen) angetragen. Sie reichen (von der Box) bis zum 0-ten bzw. 4-ten Quartil, also bis zu dem minimalen bzw. maximalen Beobachtungswert. (Variante: Die Länge der Whiskers wird durch die 1,5-fache Länge des Quartilsabstand ${\textstyle X_{0.75}-X_{0.25}}$ beschränkt. Werte außerhalb der Whiskers werden noch durch einzelne Punkte dargestellt. Damit verhindert man, das einzelne ’Ausreißer’ die Whiskers massiv beeinflussen.)

Vorraussetzung an Skala

Boxplots eignen sich nicht für Merkmale, die nur nach einer Ordinalskala verteilt sind. In dem Fall lassen sich zwar die Quartile sinnvoll definieren, aber die Einzeichnung der Skala suggeriert bestimmte Abstände zwischen den Beobachtungswerten (dies ist erst bei einer Intervallskala sinnvoll). Bei zu kleiner Datenmenge ist zu beachten, dass einzelne Beobachtungswerte einen Boxplot sehr stark beeinflussen.

Beispiele Boxplot

(vergleiche Beispiele Modalwert)

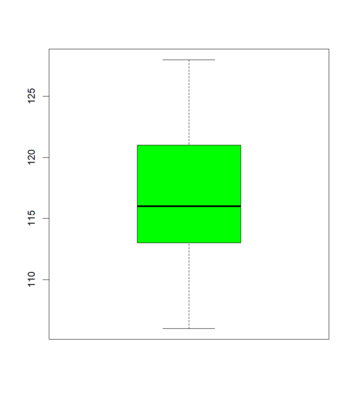
Beispiel Versuchspflanzen

Es ist: ${\textstyle \quad X_{\text{min}}=106,\quad X_{0.25}=112,\quad X_{0.5}=116,\quad X_{0.75}=122,\quad X_{\text{max}}=128}$

Beispiel Daphnien

Es ist: ${\textstyle \quad X_{\text{min}}=0,\quad X_{0.25}=1,\quad X_{0.5}=2,\quad X_{0.75}=3,\quad X_{\text{max}}=11}$

Erstellung Boxplot in R

In R: Man erstellt einen Datenvektor daten und erhält dann mit boxplot(daten,range=0) (für eine unbeschränkte Länge der Whiskers) bzw. boxplot(daten,range=1.5) (für Whiskers, die auf die ${\textstyle 1.5}$-fache Länge der Box beschränkt sind) einen Boxplot.

Histogramm und Boxplot

Interaktive Shiny-App zum Vergleich Histogramm und Boxplot:
Download und Link

Perzentilbänder

Eine weitere Darstellungsart sind die sogenannten Perzentilbänder. Wie bei Boxplots kann man darin bestimmte Quantile (Perzentile) ablesen. Perzentilbänder können auf vielfältige Art und Weise gestaltet werden.

Beispiel Perzentilband

Die unteren 5% der Schüler erreichen weniger als 300 Punkte,die oberen 5% mehr als 650 Punkte.Die mittleren 50% der Schüler (25-75%) liegen zwischen 420 und 580 Punkten.Im Mittel wird ein Leistungsniveau von 500 Punkten erreicht.

Varianz und Standardabweichung

Definition Varianz und Standardabweichung

Ist ${\textstyle X:\Omega \to \mathbb {R} }$ ein quantitatives Merkmal, so heißt
$${\text{Var}}~(X)={\frac {1}{n}}\cdot \sum \limits _{i=1}^{n}\left(X(\omega _{i})-{\overline {X}}\right)^{2}$$
(empirische) Varianz von ${\textstyle X}$ und ${\textstyle s_{X}={\sqrt {{\text{Var}}~(X)}}}$ (empirische) Standardabweichung von ${\textstyle X}$.
(Man schreibt häufig ${\textstyle {s_{X}}^{2}}$ für die Varianz von ${\textstyle X}$.)

Sind ${\textstyle a_{1},\ldots ,a_{m}}$ die Merkmalsausprägungen von ${\textstyle X}$, so gilt
$${s_{x}}^{2}={\frac {1}{n}}\cdot \sum \limits _{i=1}^{m}h(a_{i})\cdot \left(a_{i}-{\overline {X}}\right)^{2}=\sum \limits _{i=1}^{m}r(a_{i})\cdot \left(a_{i}-{\overline {X}}\right)^{2}.$$

Beispiele Varianz und Standardabweichung I

(vergleiche Beispiele Modalwert)

• Beispiel II (Versuchspflanzen): Es ist ${\textstyle {\overline {X}}=116.52}$ und ${\textstyle {s_{X}}^{2}=32.60}$ und folglich ${\textstyle s_{X}=5.71}$.

• Beispiel III (Daphnien): Es ist ${\textstyle {\overline {X}}=2.1}$ und ${\textstyle {s_{x}}^{2}=4.29}$ und folglich ${\textstyle s_{X}=2.07}$.

Weitere Formel zur Berechnung von s _x

Zur Berechnung von ${\textstyle s_{X}}$ eignet sich die Formel:

${\textstyle {s_{X}}^{2}={\frac {1}{n}}\cdot \sum \limits _{i=1}^{n}{x_{i}}^{2}-{\overline {X}}^{2}={\overline {X^{2}}}-{\overline {X}}^{2}}$

Beispiele Varianz und Standardabweichung II

In obigem Beispiel II (Versuchspflanzen) ist ${\textstyle {s_{X}}^{2}={\frac {1}{23}}\cdot \left({\begin{array}{l}\quad 110^{2}+124^{2}+120^{2}+118^{2}+111^{2}+124^{2}+128^{2}+115^{2}+119^{2}+122^{2}+106^{2}+114^{2}\\+108^{2}+117^{2}+124^{2}+117^{2}+115^{2}+109^{2}+114^{2}+114^{2}+123^{2}+112^{2}+116^{2}\end{array}}\right)-116.52^{2}=32.60}$

Varianz und lineare Verknüpfung

Für ein quantitatives Merkmal ${\textstyle X}$ und ${\textstyle a,b\in \mathbb {R} }$ gilt: ${\textstyle \quad s_{\left(a\cdot X+b\right)}=|a|\cdot s_{X}}$

Beispiel Varianz und lineare Verknüpfung

Wir betrachten das Beispiel der Temperaturangaben aus Beispiel Linearität des Mittelwerts. Dabei war ${\textstyle Y={\frac {9}{5}}X+32}$. Man berechnet: $$s_{X}=4.807\quad {\text{und}}\quad s_{Y}=8.652=\left|{\frac {9}{5}}\right|\cdot s_{X}$$

Die empirische Standardabweichung eines Merkmals ist die Wurzel aus der mittleren quadratischen Abweichung vom Mittellwert. Die Betrachtung der quadratischen Abweichung hat zur Folge, dass Ausreißer (Beobachtungswerte, die weit entfernt vom Mittlwert liegen) besonders stark gewichtet werden.

Berechnung in R I

In R: Man erstellt einen Vektor daten mit den Daten der Urliste und kann dann mit mean(daten^2)-mean(daten)^2 die Varianz ${\textstyle {s_{x}}^{2}}$ beziehungsweise mit sqrt(mean(daten^2)-mean(daten)^2) die Standardabweichung ${\textstyle s_{X}}$ berechnen.

Berechnung in R II

Alternativ kann man mit var(daten) die sogenannte korrigierte Stichprobenvarianz
$${\frac {1}{n-1}}\cdot \sum \limits _{i=1}^{n}\left(X(\omega _{i})-{\overline {X}}\right)^{2}={\frac {n}{n-1}}{s_{X}}^{2}$$
und mit sd(daten) die Wurzel daraus, also
$${\sqrt {{\frac {1}{n-1}}\cdot \sum \limits _{i=1}^{n}\left(X(\omega _{i})-{\overline {X}}\right)^{2}}}={\sqrt {\frac {n}{n-1}}}s_{X}$$
berechnen. (Die Berechnung dieses Ausdrucks macht in der schließenden Statistik Sinn, siehe Vorlesung ’Statistik für Anwender II’.)

Aufgabe I

Gegeben Sei die Grundgesamtheit aller Kinder von Ehepaaren (${\textstyle n=50}$):
$${\begin{array}{|c||c|c|c|c|c|c|c|c|c|}\hline {\text{Zahl der Nachkommen }}a&0&1&2&3&4&5&8&11\\\hline {\text{absolute Häufigkeit }}h(a)&10&13&11&7&5&2&1&1\\\hline \end{array}}$$

• Berechnen Sie für das Merkmal "Zahl der Geschwister" den Modalwert, den Median, den arithmetischen Mittelwert.
  Hinweis: Bestimmen Sie zunächst die möglichen Merkmalsausprägungen und ihre absoluten Häufigkeiten.
• Bestimmen Sie die Spannweite, Varianz und Standardabweichung sowohl für die Anzahl der Kinder als auch für die Anzahl der Geschwister.

Aufgabe II

In einem Versuch zum Wachstum der Sprossachse einer bestimmten Art werden die folgenden Werte in mm ermittelt:
8, 2, 15, 16, 7, 11, 4, 19, 11, 12, 13, 9, 5, 6, 8, 13, 6, 14, 17, 8

• Bestimmen Sie Median, Modalwert und arithmetisches Mittel.
• Bestimmen Sie die Spannweite, Varianz und Standardabweichung.
• Berechnen Sie die absoluten und relative Häufigkeit zur Klassierung mit den folgenden Grenzen: $$k_{0}=0,\quad k_{1}=5,\quad k_{2}=10,\quad k_{3}=15,\quad k_{4}=20\quad$$
  Berechnen Sie dann auch die Häufigkeitsdichten und erstellen Sie ein Histogramm.
  

Standardisierte Merkmale

Definition standardisiertes Merkmal

Ein (quantitatives) Merkmal ${\textstyle X}$ heißt standardisiert, falls ${\textstyle {\overline {X}}=0}$ und ${\textstyle s_{X}=1}$ ist.

Normalerweise treten bei Beobachtungen praktisch nie standardisierte Merkmale auf. Man kann aber jedes Merkmal mit einer einfachen Transformation standadisieren. Es gilt: Ist ${\textstyle X:\Omega \to \mathbb {R} }$ ein quantitatives Merkmal, so ist $${\hat {X}}={\frac {X-{\overline {X}}}{s_{X}}}:\Omega \to \mathbb {R} ,\ {\hat {X}}(\omega )={\frac {X(\omega )-{\overline {X}}}{s_{X}}}$$
ein standardisiertes Merkmal. Man nennt ${\textstyle {\hat {X}}}$ standardisiertes Merkmal zu ${\textstyle X}$.

Anmerkung standardisiertes Merkmal I

Für einen Merkmalsträger ${\textstyle \omega \in \Omega }$ entspricht ${\textstyle {\hat {X}}(\omega )}$ dem Unterschied von ${\textstyle X(\omega )}$ und dem Mittelwert von ${\textstyle X}$ gemessen in Standardabweichungen. Man beachte: $${\hat {X}}(\omega )={\frac {X(\omega )-{\overline {X}}}{s_{X}}}\quad \Leftrightarrow \quad X(\omega )={\overline {X}}+{\hat {X}}(\omega )\cdot s_{X}$$

Beispiel standardisiertes Merkmal 1

(vergleiche Beispiele Modalwert)

• Beispiel II (Versuchspflanzen):
  • Es ist ${\textstyle {\overline {X}}=116.52}$ und ${\textstyle s_{X}=5.71}$.
  • Ist ${\textstyle \omega _{1}}$ ein Spross mit ${\textstyle X(\omega _{1})=128}$, so ist ${\textstyle {\hat {X}}(\omega _{1})=2.01}$. Damit ist der Spross um ${\textstyle 2.01}$ Standardabweichungen größer als das arithmetische Mittel aller Sprossen aus der untersuchten Grundgesamtheit.
  • Ist ${\textstyle \omega _{2}}$ ein Spross mit ${\textstyle X(\omega _{2})=112}$, so ist ${\textstyle {\hat {X}}(\omega _{2})=-0.79}$. Damit ist der Spross um ${\textstyle 0.79}$ Standardabweichungen kleiner als das arithmetische Mittel aller Sprossen aus der untersuchten Grundgesamtheit.

Beispiel standardisiertes Merkmal 2

• • Ist ${\textstyle \omega _{3}}$ ein Spross mit ${\textstyle X(\omega _{3})=117}$, so ist ${\textstyle {\hat {X}}(\omega _{3})=0.08}$. Damit ist der Spross um ${\textstyle 0.08}$ Standardabweichungen größer als das arithmetische Mittel aller Sprossen aus der untersuchten Grundgesamtheit.

• Beispiel III (Daphnien):
  • Es ist ${\textstyle {\overline {X}}=2.1}$ und ${\textstyle s_{X}=2.07}$. Für eine Daphnie ${\textstyle \omega }$ mit ${\textstyle X(\omega )=11}$ gilt ${\textstyle {\hat {X}}(\omega )={\frac {11-2.1}{2.07}}=4.30}$. Die Kinderzahl der Familie ist also um ${\textstyle 4.3}$ Standardabweichungen größer als der Durchschnitt (arithmetisches Mittel) aller Familien aus der untersuchten Grundgesamtheit.

Anmerkung standardisiertes Merkmal II

Für ${\textstyle a,b\in \mathbb {R} }$ mit ${\textstyle a\not =0}$ gilt $${\widehat {\left(a\cdot X+b\right)}}={\begin{cases}{\hat {X}}&,\;{\text{falls}}\ a>0\\-{\hat {X}}&,\;{\text{falls}}\ a<0\end{cases}}.$$

Aufgabe 1.1

Zwei Speerwerfer ${\textstyle X}$ und ${\textstyle Y}$ absolvieren jeweils eine Trainingsserie und erzielen dabei die folgenden Weiten:

$$X\quad (n=15)$$
$${\begin{array}{|c||c|c|c|c|c|c|c|c|c|}\hline 46.2&47.5&51.5&54.6&37.5&37.3&44.3&44.9&35.3&50.1&48.2&49.1&59.3&44.6&55.9\\\hline \end{array}}$$

$$Y\quad (n=12)$$
$${\begin{array}{|c||c|c|c|c|c|c|c|c|c|}\hline 38.7&48.1&44.2&49.7&38.6&41.3&40.9&43.0&45.1&40.3&43.1&49.9\\\hline \end{array}}$$

• Berechnen Sie jeweils den Median und den arithmetischen Mittelwert.
• Berechnen Sie jeweils die Spannweite, die empirische Varianz und die empirische Standardabweichung.

Aufgabe 1.2

• Beide waren der Meinung, dass ihr letzter Wurf besonders gut war. Benutzen Sie die standardisierten Merkmale ${\textstyle {\hat {X}}}$ und ${\textstyle {\hat {Y}}}$, um dies zu beurteilen.

Aufgabe 2

Diskutieren Sie: Wie wirkt sich das Vergrößern des Datensatzes auf die die verschiedenen Lage- und Streuungsmaße aus?

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Streuma%C3%9Fe
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.