Situation: Gegeben sind  normalverteilte ZV
normalverteilte ZV  deren Standardabweichungen
deren Standardabweichungen  (bzw. Varianzen) gleich sind.
(bzw. Varianzen) gleich sind.
Hypothesenpaar: 
Äquivalent dazu (unter obigen Voraussetzungen): 

 unabhängige Stichproben
unabhängige Stichproben

Man berechnet aus den Stichproben:
- die Gruppenmittelwerte (’mean of groups’):

- den Gesamtmittelwert (’grand mean’):

Beachte: Es gilt: 
- Die Summe der quadratischen Abweichungen aller Stichprobenwerte
 vom Gesamtmittelwert
vom Gesamtmittelwert  bezeichnet man mit:
bezeichnet man mit: 
- Weiterhin bezeichnet man die Summe der quadratischen Abweichungen aller Stichprobenmittelwerte
 vom Gesamtmittelwert
vom Gesamtmittelwert  mit:
mit: 

SST ist ein Maß für die Unterschiede zwischen den verschiedenen Stichproben.
- Schließlich bezeichnet man die Summe der quadratischen Abweichungen aller Stichprobenwerte
 vom jeweiligen Stichprobenmittelwerte
vom jeweiligen Stichprobenmittelwerte  mit:
mit:  SSE ist ein Maß für die Unterschiede innerhalb der einzelnen Stichproben.
SSE ist ein Maß für die Unterschiede innerhalb der einzelnen Stichproben.
Man beachte, dass gilt: 
Man teilt nun SST und SSE durch die Zahl der jeweiligen Freiheitsgrade (falls  gilt, sind
gilt, sind  und
und  jeweils
jeweils  -verteilt mit
-verteilt mit  bzw.
bzw.  FG) und erhält die sogenannten ’mittleren quadratischen Abweichungen’
FG) und erhält die sogenannten ’mittleren quadratischen Abweichungen’ 
Aus SST und SSE berechnet man nun die Teststatistik wie folgt: 
Idee: MSE stellt eine Schätzung für die Streuung innerhalb der einzelnen Stichproben dar. Im Gegensatz dazu schätzt MST die Streuung der verschiedenen Stichprobenmittelwerte um den Gesamtmittelwert. Nimmt man an, dass  gilt, sollte MST (im Vergleich zu MSE) klein sein, folglich ist
gilt, sollte MST (im Vergleich zu MSE) klein sein, folglich ist  eine Teststatistik, bei der man eher kleine Werte erwartet, falls
eine Teststatistik, bei der man eher kleine Werte erwartet, falls  gilt.
gilt.
Zur Berechung wird die F-Verteilung (bzw. Fisher-Verteilung)  mit den ’Freiheitsgraden’
mit den ’Freiheitsgraden’  und
und  benötigt. Es gilt:
benötigt. Es gilt: 
(Dies geht in R mit  .)
.)
Einlesen der Stichproben in einen gemeinsamen Vektor x zusammen mit einem Faktor g (gleicher Länge), der angibt, zu welcher Größe die jeweiligen Komponenten von x gehören. Dann: 

Verschiedene Drahtsorten ( ) werden auf Zugfestigkeit untersucht. Dabei soll zu
) werden auf Zugfestigkeit untersucht. Dabei soll zu  geprüft werden, ob die verschiedenen Drahtsorten (oder einige der Sorten) im erwarteten Mittel unterschiedliche Zugfestigkeiten aufweisen. Dazu nimmt man an, dass die ZV
geprüft werden, ob die verschiedenen Drahtsorten (oder einige der Sorten) im erwarteten Mittel unterschiedliche Zugfestigkeiten aufweisen. Dazu nimmt man an, dass die ZV  , die die Zugfestigkeiten der verschiedenen Sorten beschreiben, normalverteilt mit gleicher Varianz sind und formuliert die Nullhypothese:
, die die Zugfestigkeiten der verschiedenen Sorten beschreiben, normalverteilt mit gleicher Varianz sind und formuliert die Nullhypothese:

Man erhält folgende Daten (in  ):
):

Daraus berechnet sich:
 und
und 
Folglich zeigen die Daten keine siginifikanten Unterschiede zwischen den Zugfestigkeiten der verschiedenen Drahtsorten. Die Nullhypothese ist mit den Daten vereinbar.
Man kann obige Rechnungen auch in R durchführen lassen. Dies geht etwa mit 
- Die oben genannten Voraussetzungen für die Varianzanalyse mit dem F-Test können (und sollten) mit Hilfe von Vortests empirisch geprüft werden. Die Normalverteilungsannahme kann mit Shapiro-Wilks-Tests für jede der ZV
 getestet werden. Die Annahme der Varianzgleichheit kann man dann mit einem sogenannten Bartlett-Test prüfen. Liefert einer der Vortests ein signifikantes Ergebnis (bzw. einen kleinen
getestet werden. Die Annahme der Varianzgleichheit kann man dann mit einem sogenannten Bartlett-Test prüfen. Liefert einer der Vortests ein signifikantes Ergebnis (bzw. einen kleinen  -Wert), so kann der F-Test nicht verwendet werden. Man muss dann auf andere Testverfahren zurückgreifen. Beispielsweise kann dann der Test von Kruskal und Wallis verwendet werden.
-Wert), so kann der F-Test nicht verwendet werden. Man muss dann auf andere Testverfahren zurückgreifen. Beispielsweise kann dann der Test von Kruskal und Wallis verwendet werden.
- Falls die Varianzanalyse ein signifikantes Ergebnis liefert, wird dadurch lediglich angezeigt, dass nicht alle
 gleich sind. Zur Klärung der Frage,welche der
gleich sind. Zur Klärung der Frage,welche der  signifikant als verschieden angesehen werden können, stehen weitere Testverfahren zur Verfügung, bespielsweise der Scheffé-Test oder der Tukey-Test.
signifikant als verschieden angesehen werden können, stehen weitere Testverfahren zur Verfügung, bespielsweise der Scheffé-Test oder der Tukey-Test.
In einer Studie soll untersucht werden, wie sich die Wildschweinpopulationsdichte auf den Traubenertrag im Weinbau auswirkt. Für die Studie wurden 3 Gebiete identifiziert, in denen Weinbau betrieben wird, die jedoch unterschiedliche Populationsdichten an Wildschweinen aufweißen. In jedem Gebiet befinden sich unterschiedlich viele Versuchsflächen, die jeweils gleich bewirtschaftet werden. Bei jeder Testfläche wurde am Ende der Traubensaison der Ertrag an Trauben in Tonnen pro Hektar ermittelt. Es ergeben sich folgende Daten:

- Worauf sollte bei der Auswahl der Testgebiete geachtet werden? (Stichwort Randeffekte)
- Überprüfen Sie mit dem Shapiro-Wilks- und dem Bartlett-Test (in R - keine Rechnung notwendig), ob die Voraussetzungen für die Einfaktorielle Varianzanalyse gegeben sind.
Der Tukey-Test (bzw. die Tukey-Methode)
[Bearbeiten]Situation, Signifikanzniveau und Nullhypothese
[Bearbeiten]Situation: Gegeben sind  normalverteilte ZV
normalverteilte ZV  deren Standardabweichungen
deren Standardabweichungen  (bzw. Varianzen) gleich sind.
(bzw. Varianzen) gleich sind.
Signifikanzniveau: Es muss ein Signifikanzniveau  festgelegt werden.
festgelegt werden.
Nullhypothesen:  für
für  mit
mit 
Alle diese Nullhypothesen werden gemeinsam getestet. Das bedeutet: Falls alle  wahr sind, erhält man höchstens mit Wahrscheinlichkeit
wahr sind, erhält man höchstens mit Wahrscheinlichkeit  mindestens ein signifikantes Ergebnis.
mindestens ein signifikantes Ergebnis.
benötigte Daten:  unabhängige Stichproben gleicher Länge
unabhängige Stichproben gleicher Länge 

Die Gesamtlänge  ergibt sich dann offenbar als
ergibt sich dann offenbar als  .
.
Teststatistik: Man berechnet zunächst paarweise die (betragsmäßigen) Differenzen der empirischen Mittelwerte, also 
und die mittlere quadratische Abweichung der Fehler 
Daraus berechnen sich die Teststatistiken als 
Offenbar sprechen hohe Werte dieser Statistik gegen  .
.
 -Werte: Zur Berechung wird die studentisierte Spannweite
-Werte: Zur Berechung wird die studentisierte Spannweite  mit den ’Freiheitsgraden’
mit den ’Freiheitsgraden’  und
und  benötigt. Zur Nullhypothese
benötigt. Zur Nullhypothese  ist der
ist der  -Wert gegeben durch:
-Wert gegeben durch:

(Dies geht in R mit ptukey(x,m,n-m).)
Für die Paare  , deren
, deren  -Wert kleiner oder gleich
-Wert kleiner oder gleich  sind, kann also die entsprechende Nullhypothese
sind, kann also die entsprechende Nullhypothese  verworfen werden. Man hat dann ein oder mehrere signifikante Ergebnisse zum gemeinsamen Niveau
verworfen werden. Man hat dann ein oder mehrere signifikante Ergebnisse zum gemeinsamen Niveau  , d.h. es wurde berücksichtigt, dass man mehrere Nullhypothesen getestet hat.
, d.h. es wurde berücksichtigt, dass man mehrere Nullhypothesen getestet hat.
Einlesen der Stichproben in einen gemeinsamen Vektor x zusammen mit einem Faktor g (gleicher Länge), der angibt, zu welcher Größe die jeweiligen Komponenten von x gehören. Dann: 
Zur Ausgabe gehören neben den  -Werten der einzelnen Nullhypothesen auch Konfidenzintervalle zum (gemeinsamen) Niveau
-Werten der einzelnen Nullhypothesen auch Konfidenzintervalle zum (gemeinsamen) Niveau  für die Differenzen der wahren Erwartungswerte
für die Differenzen der wahren Erwartungswerte  . Diese Intervalle lassen sich mit
. Diese Intervalle lassen sich mit  auch graphisch darstellen.
auch graphisch darstellen.
Das bedeutet, dass (falls alle  gelten) die Wahrscheinlichkeit, dass alle berechneten Konfidenzintervalle die entsprechende wahre Erwartungswertdifferenz enthalten, mindestens
gelten) die Wahrscheinlichkeit, dass alle berechneten Konfidenzintervalle die entsprechende wahre Erwartungswertdifferenz enthalten, mindestens  ist.
ist.
Für unterschiedliche Stichprobenlänge  von
von  berechnet man die Teststatistiken wie folgt (Tukey-Kramer-Methode):
berechnet man die Teststatistiken wie folgt (Tukey-Kramer-Methode):

Wir betrachten die folgenden Stichproben ( ) zum Signifikantsniveau
) zum Signifikantsniveau  .
.

Man berechnet  und
und  . Damit ergibt sich der
. Damit ergibt sich der  -Wert einer Varianzanalyse mit einem
-Wert einer Varianzanalyse mit einem  -Tests zur Nullhypothese als
-Tests zur Nullhypothese als  . Man kann also davon ausgehen, dass sich Erwartungswerte einiger der Größen unterscheiden.
. Man kann also davon ausgehen, dass sich Erwartungswerte einiger der Größen unterscheiden.
Man möcht nun genauer wissen, welche der Erwartungswerte sich im einzelnen unterscheiden. Dazu führt man einen Tukey-Test durch. Insgesamt werden dabei 10 Vergleiche durchgeführt:

Damit wird also signifikant angezeigt, dass sich die Großen  und
und  und auch die Großen
und auch die Großen  und
und  hinsichtlich ihrer Erwartungswerte unterscheiden.
hinsichtlich ihrer Erwartungswerte unterscheiden.
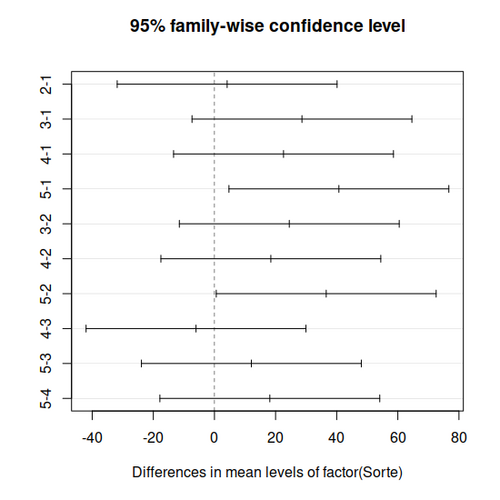
Legt man ein Signifikanzniveau  fest, so kann man mit TukeyHSD eine Graphik erzeugen, die Konfidenzintervalle zum gemeinsamen Niveau
fest, so kann man mit TukeyHSD eine Graphik erzeugen, die Konfidenzintervalle zum gemeinsamen Niveau  zeigt:
zeigt:
Nehmen Sie nun an, dass Sie in der vorherigen Aufgabe ein Signifikantes Ergebnis erhalten hätten. Berechnen Sie nun mithilfe der Tukey-Methode, zwischen welchen Gruppen signifikante Unterschiede existieren.
Es soll untersucht werden, ob eine ZV  (Zielvariable) durch zwei vorliegende Faktoren
(Zielvariable) durch zwei vorliegende Faktoren  und
und  beeinflusst wird. Die Faktoren
beeinflusst wird. Die Faktoren  und
und  nehmen dabei nur endlich viele Werte (bzw. Ausprägungen) an (
nehmen dabei nur endlich viele Werte (bzw. Ausprägungen) an ( Möglichkeiten für
Möglichkeiten für  und
und  Möglichkeiten für
Möglichkeiten für  ).
).
Man unterscheidet nun ZV

wobei  die Größe
die Größe  für die
für die  -te Ausprägung von
-te Ausprägung von  und die
und die  -te Ausprägung von
-te Ausprägung von  ist
ist  .
.
Vorausgesetzt für den folgenden Test wird, dass alle  normalverteilt mit gleicher Varianz sind.
normalverteilt mit gleicher Varianz sind.
Man untersucht dabei die Nullhypothesen



Zu jeder der  vielen Größen benötigt man nun eine Stichprobe
vielen Größen benötigt man nun eine Stichprobe

(Wir gehen der Einfachheit halber davon aus, dass alle Stichproben die gleiche Länge haben. Für ungleiche Stichprobenlängen wird es nochmals erheblich komplizierter.)
Daraus berechnet man nun die folgenden Mittelwerte und Stichprobenlängen:
- Einzelne Stichprobe (
 fest):
fest): 
- Mit festem Wert für
 zusammengefasste Stichprobe (
zusammengefasste Stichprobe ( fest):
fest): 
Zu berechnende Werte und Parameter III
[Bearbeiten]- Mit festem Wert für
 zusammengefasste Stichprobe (
zusammengefasste Stichprobe ( fest):
fest): 
- Gesamte Stichprobe:

Es gilt die folgende Quadratsummenzerlegung: 
Dabei ist:

Zu den oben angegebenen Nullhypothesen berechnet man nun Teststatistik und  -Wert wie folgt:
-Wert wie folgt:

Man kann diese auch mit R durchführen. Man trägt dazu in einen Vektor x die Daten ein und in zwei Faktoren a und b (beide haben die gleiche Länge wie x) die Information, zu welcher Ausprägung von  bzw.
bzw.  die Daten gehören. Dann erhält man mit:
die Daten gehören. Dann erhält man mit:

die benötigten Werte (Freiheitsgrade, Quadratsummen, mittlere Quadratsummen, Teststatistiken,  -Werte).
-Werte).
Gegeben seien die Faktoren  und
und  mit den Ausprägungen
mit den Ausprägungen  und
und  , dem Signifikanzniveau
, dem Signifikanzniveau  und der folgenden Stichprobe:
und der folgenden Stichprobe:

Es ergibt sich:

Somit kann die Nullhypothese, dass  unabhängig von
unabhängig von  ist, verworfen werden.
ist, verworfen werden.
Weiterhin ergibt sich:

Somit kann auch diese Nullhypothese, dass  unabhängig von
unabhängig von  ist, verworfen werden.
ist, verworfen werden.
Weiterhin ergibt sich:
 Die Nullhypothese, dass es keine Wechselwirkung zwischen
Die Nullhypothese, dass es keine Wechselwirkung zwischen  und
und  im Hinblick auf
im Hinblick auf  gibt, kann nicht wiederlegt werden, somit ist es anzunehmen, dass es keine Wechselwirkung gibt.
gibt, kann nicht wiederlegt werden, somit ist es anzunehmen, dass es keine Wechselwirkung gibt.
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.