Kurs:Statistik für Anwender/Darstellung eindimensionaler Merkmale

Darstellung eindimensionaler Merkmale

Urliste

Für ein Merkmal ${\textstyle X:\Omega \to A}$ mit einer Grundgesamtheit ${\textstyle \Omega =\{\omega _{1},\ldots ,\omega _{n}\}}$ bezeichnet man die tabellarische Darstellung
$${\begin{array}{|c|c|c|c|}\hline \omega _{1}&\omega _{2}&\quad \ldots \quad &\omega _{n}\\\hline X(\omega _{1})&X(\omega _{2})&\ldots &X(\omega _{n})\\\hline \end{array}}$$
als Urliste des Merkmals. Die Urliste enthält alle Informationen des Merkmals, diese sind allerdings nicht geordnet. Auch die Auflistung der Beobachtungswerte $$X(\omega _{1}),\ X(\omega _{2}),\ \ldots ,\ X(\omega _{n})$$
bezeichnet man als Urliste (Kurzform).

$$x_{1}\leq x_{2}\leq \ldots \leq x_{n}$$
der Beobachtungswerte die geordnete Datenreihe.

Beispiel Urliste und geordnete Datenreihe

In einer Klassenarbeit erhielten die Schüler einer Klasse folgende Noten (Urliste): $${\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline \omega _{1}&\omega _{2}&\omega _{3}&\omega _{4}&\omega _{5}&\omega _{6}&\omega _{7}&\omega _{8}&\omega _{9}&\omega _{10}&\omega _{11}&\omega _{12}\\\hline 2&3&6&4&2&2&1&4&5&3&3&2\\\hline \hline \omega _{13}&\omega _{14}&\omega _{15}&\omega _{16}&\omega _{17}&\omega _{18}&\omega _{19}&\omega _{20}&\omega _{21}&\omega _{22}&\omega _{23}&\omega _{24}\\\hline 3&3&5&1&2&4&3&4&5&2&1&3\\\hline \end{array}}$$ Daraus ergibt sich die geordnete Datenreihe: $$1,1,1,2,2,2,2,2,2,3,3,3,3,3,3,3,4,4,4,4,5,5,5,6$$

Absolute und relative Häufigkeiten

Für ein Merkmal ${\textstyle X:\Omega \to A}$ mit einer Grundgesamtheit ${\textstyle \Omega =\{\omega _{1},\ldots ,\omega _{n}\}}$ bezeichnet man zu einer Merkmalsausprägung ${\textstyle a\in A}$

• die natürliche Zahl
  $$h(a)=\left|\{\omega \in \Omega ;\ X(\omega )=a\}\right|$$
  als absolute Häufigkeit der Merkmalsausprägung ${\textstyle a}$.
• den Quotienten
  $$r(a)={\frac {h(a)}{n}}$$
  als relative Häufigkeit der Merkmalsausprägung ${\textstyle a}$.

Ist ${\textstyle A=\{a_{1},\ \ldots ,a_{m}\}}$, so gilt $$\sum _{i=1}^{m}h(a_{i})=n\quad {\text{und}}\quad \sum _{i=1}^{m}r(a_{i})=1$$

Beispiel absolute und relative Häufigkeiten

In obigem Beispiel der Noten der Schüler ist
${\textstyle {\begin{array}{|c|c|c|c|c|c|c|}\hline {\text{a}}&1&2&3&4&5&6&{\text{ges}}\\\hline h(a)&3&6&7&4&3&1&24\\\hline r(a)&{\frac {3}{24}}&{\frac {6}{24}}&{\frac {7}{24}}&{\frac {4}{24}}&{\frac {3}{24}}&{\frac {1}{24}}&1\\\hline \end{array}}}$

Verschiedene einfache Diagramme

Die folgenden Darstellungen sind schon bei nominalskalierten Merkmalen geeignet:

• Säulen- bzw. Balkendiagramm: Absolute oder relative Häufigkeiten werden als Höhe von Säulen bzw. Balken dargestellt.
• Kreisdiagramm: Relative Häufigkeiten werden als Anteile eines Kreises (in Form eines Sektors dargestellt). Der Winkel des Sektors zu einer Merkmalsausprägung ${\textstyle a}$ beträgt dabei ${\textstyle r(a)\cdot 360^{\circ }={\frac {h(a)\cdot 360^{\circ }}{n}}}$.
• Stapeldiagramm: Relative Häufigkeiten werden als Flächen in einer Rechtecksäule dargestellt.

Beispiel Kreisdiagramm

In obigem Beispiel ergeben sich das folgende Kreisdiagramm:

Beispiel Säulendiagramm

Und das folgende Säulendiagramm

Erstellung Kreis- und Säulendiagramm in R

In R: Man trage die möglichen Merkmalsausprägungen und die zugehörigen absoluten Häufigkeiten in Vektoren ein, z.B.

note ${\textstyle \color {blue}<-}$c(”1” , ”2” , ”3” , ”4” , ”5” ,”6”)

und

anzahl ${\textstyle \color {blue}<-}$ c(3,6,7,4,3,1) und kann dann mit pie(anzahl,note) ein Kreisdiagramm und barplot(anzahl,names.arg=note) ein Säulendiagramm erstellen.

Klassierung von Daten

Um Ergebnisse übersichtlich darzustellen und um bestimmte Sachverhalte hervorzuheben, ist es oft notwendig/sinnvoll die Merkmalsausprägungen in bestimmten Gruppen (Klassen) zusammenzufassen. Damit können die Daten weniger fein aber hinreichend informativ dargestellt werden. (Was hinreichend ist, hängt vom Verwendungszweck und der Darstellung der Daten ab.)

Klasseneinteilung

Für ein Merkmal ${\textstyle X}$ mit einer Grundgesamtheit ${\textstyle \Omega =\{\omega _{1},\ldots ,\omega _{n}\}}$ kann man auch eine Klassierung (oder Klasseneinteilung) vornehmen. Dazu unterteilt man die Menge der möglichen Ausprägungen in verschiedene (überschneidungsfreie) Klassen. Jede Merkmalsausprägung ist damit in genau einer Klasse enthalten.

Klassenhäufigkeit

Zu jeder Klasse ${\textstyle K}$ betrachtet man nun ihre absolute und ihre relative Häufigkeit: $$h(K)=\left|\left\{\omega \in \Omega ;\ X(\omega )\in K\right\}\right|\quad {\text{und}}\quad r(K)={\frac {h_{j}}{n}}$$
Sind ${\textstyle K_{1},\ldots ,K_{m}}$ die verschiedenen Klassen, so gilt: $$\sum \limits _{j=1}^{m}h(K_{j})=n\quad {\text{und}}\quad \sum \limits _{j=1}^{m}r(K_{j})=1.$$
Da dabei Informationen verloren gehen, sollte man bei der Einteilung der verschiedenen Klassen im Hinblick auf Verwendungszweck und Informationsgehalt sehr sorgfältig sein bzw. klassierte Daten mit Bedacht zur Kenntnis nehmen.

Beispiel Klassierung I

Das folgende Säulendiagramm stellt die relativen Häufigkeiten der Zweitstimmenanteile der Parteien bei der Bundestagswahl 2009 dar:

Hierbei wurden CDU und CSU (eine Fraktion) zu einer Klasse zusammengefasst (aber noch farblich getrennt) und alle Parteien, die weniger als 5% der Stimmen erreicht haben, zu der Klasse ’Sonstige’ zusammengefasst.

Beispiel Klassierung II

Der Hamburger Sportverein (HSV) erzielte in der Fußball-Bundesliga in 20 aufeienanderfolgenden Spielzeiten die folgenden Platzierungen (Urliste): $$5,12,11,12,13,5,13,9,7,3,13,11,4,8,8,3,7,4,5,7$$ Säulendiagramme zu zwei (mit besonderer Absicht gewählten) Klassierungen:

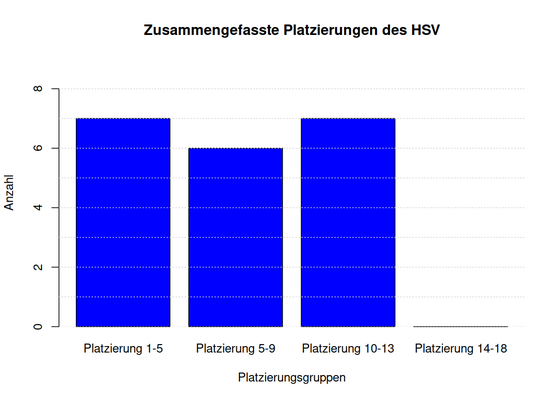
Beispiel Klassierung IIa

Klassen mit Plätze 1-5, Plätze 6-9, Plätze 10-13, Plätze 14-18:

Beispiel Klassierung IIb

Klassen mit Plätze 1-2, Plätze 3-6, Plätze 7-10, Plätze 11-18

Auswahl von Klassen I

Für die Auswahl von Klassen gibt es viele Möglichkeiten. Je nach Auswahl der Klassen kann das präsentierte Ergebnis (obgleich es stets der Wahrheit entspricht) sehr unterschiedliche Wirkung haben.

• Um eine gewisse Objektivität zu gewährleisten, sollte die Einteilung in die verschiedenen Klassen vor der Datenerhebung geschehen. Will man nachträglich noch eine Veränderung der Klassen vornehmen, sollte man dies inhaltlich begründen können.
• Eine Fautsregel besagt, dass bei ${\textstyle n}$ untersuchten Merkmalsträgern, die Zahl der Klassen etwa ${\textstyle {\sqrt {n}}}$ sein sollte. Dies ist sicher nicht in allen Fällen sinnvoll, kann aber ein Anhaltspunkt sein.

Auswahl von Klassen II

• Bei quantitativen Merkmalen ist die Entscheidung, ob man Intervalle gleicher oder verschiedener Länge als Klassen verwenden will, zu treffen und nach Möglichkeit inhaltlich zu begründen.

Die Frage nach der Einteilung der Klassen lässt sich in allgemeinem Rahmen nicht mathematisch ableiten. Man muss sie daher im Einzelfall ’mit gesundem Menschenverstand’ angehen.

Histogramm

Bildung von Klassen

Wir betrachten nun ein quantitatives (d.h. mindestens nach einer Intervallskala verteiltes) Merkmal ${\textstyle X:\Omega \to \mathbb {R} }$ mit Grundgesamtheit ${\textstyle \Omega =\{\omega _{1},\ldots ,\omega _{n}\}}$. Nimmt man dabei Klassierungen vor, so ist es (meist) sinnvoll die Klassen als (halboffene) Intervalle zu wählen. Man wählt dazu zunächst ${\textstyle m+1}$ Intervallgrenzen
$$k_{0}<k_{1}<k_{2}<\ldots <k_{m-1}<k_{m},$$
derart dass alle möglichen Merkmalsausprägungen ${\textstyle X(\omega _{i})\in ]k_{0},k_{m}]}$ liegen (dabei kann auch ${\textstyle k_{0}=-\infty }$ und/oder ${\textstyle k_{m}=\infty }$ gewählt werden) und betrachtet dann die ${\textstyle m}$ Klassen: $$K_{1}=]k_{0},k_{1}],\quad K_{2}=]k_{1},k_{2}],\quad \ldots ,K_{m}=]k_{m-1},k_{m}]$$

Klassenhäufigkeit

Dann gehört jede Merkmalsausprägung zu genau einer der Klassen ${\textstyle K_{j}}$ und man kann jeder Klasse eine absolute Häufigkeit ${\textstyle h_{j}=h(K_{j})}$ und eine relative Häufigkeit ${\textstyle r_{j}=r(K_{j})={\frac {h_{j}}{n}}}$ zuordnen.

Klassenhäufigkeitsdichte

Weiterhin betrachtet man zu jeder Klasse ${\textstyle K_{j}=]k_{j-1},k_{j}]}$ die jeweilige Klassenbreite ${\textstyle b_{j}=k_{j}-k_{j-1}}$ (Intervalllänge) und ermittelt daraus die Häufigkeitsdichte ${\textstyle f_{j}={\frac {r_{j}}{b_{j}}}}$ innerhalb von ${\textstyle K_{j}}$. Die Funktion $${\hat {f}}_{X}^{(k_{0},\ldots ,k_{m})}:\mathbb {R} \to \mathbb {R} ,\quad x\mapsto \{{\begin{array}{ccl}f_{j}&,&{\text{falls}}\ x\in K_{j}\ {\text{für ein}}\ j\\0&,&{\text{sonst}}\end{array}}.$$ heißt Häufigkeitsdichtefunktion von ${\textstyle X}$ bezüglich der Klassierung ${\textstyle K_{j}\ (j=1,\ldots ,m)}$. Ihren Graphen bezeichnet man als Histogramm.

Beispiel Histogramm

Gegeben sei folgende Urliste eines Merkmals ${\textstyle X}$ (mit ${\textstyle n=20}$): $$46.5,\ 45.3,\ 65.4,\ 48.0,\ 51.2,\ 29.0,\ 51.5,\ 42.1,\ 66.5,\ 49.6,$$ $$39.2,\ 32.7,\ 45.5,\ 61.4,\ 24.9,\ 58.2,\ 7.3,\ 36.3,\ 51.4,\ 43.8$$
Wir betrachten die folgenden durch Intervallgrenzen gegebenen Klassierungen:

Beispiel Klassierung I

${\textstyle k_{0}=0,\ k_{1}=10,\ k_{2}=20,\ k_{3}=30,\ k_{4}=40,\ k_{5}=50,\ k_{6}=60,\ k_{7}=70}$

${\textstyle {\begin{array}{|c|c|c|c|c|c|c|}\hline K_{j}=]k_{j-1},k_{j}]&]0,10]&]10,20]&]20,30]&]30,40]&]40,50]&]50,60]&]60,70]\\\hline h_{j}=h(K_{j})&1&0&2&3&7&4&3\\\hline r_{j}=r(K_{j})&0.05&0&0.1&0.15&0.35&0.2&0.15\\\hline b_{j}=k_{j}-k_{j-1}&10&10&10&10&10&10&10\\\hline f_{j}={\frac {r_{j}}{b_{j}}}&0.005&0&0.01&0.015&0.035&0.02&0.015\\\hline \end{array}}}$

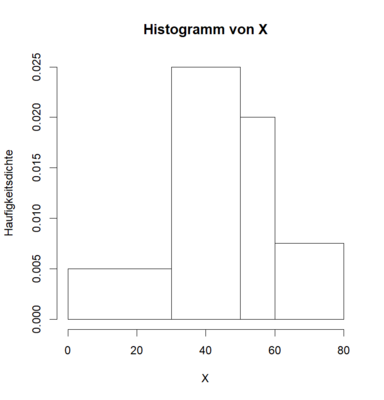
Beispiel Klassierung II

${\textstyle k_{0}=0,\ k_{1}=30,\ k_{2}=50,\ k_{3}=60,\ k_{4}=80}$

${\textstyle {\begin{array}{|c|c|c|c|}\hline K_{j}=]k_{j-1},k_{j}]&]0,30]&]30,50]&]50,60]&]60,80]\\\hline h_{j}=h(K_{j})&3&10&4&3\\\hline r_{j}=r(K_{j})&0.15&0.5&0.2&0.15\\\hline b_{j}=k_{j}-k_{j-1}&30&20&10&20\\\hline f_{j}={\frac {r_{j}}{b_{j}}}&0.005&0.025&0.02&0.0075\\\hline \end{array}}}$

Anmerkungen Histogramm I

• Anstatt ${\textstyle ]k_{j-1},k_{j}]}$ hätte man auch Intervalle der Form ${\textstyle [k_{j-1},k_{j}[}$ betrachten können.
• Die Fläche des ${\textstyle j}$-ten Rechtecks im Histogramm beträgt $${\text{Breite}}\cdot {\text{Höhe}}=b_{j}\cdot f_{j}=r_{j}.$$
  Da sich die relativen Häufigkeiten zu ${\textstyle 1}$ summieren, beträgt die Summe der Flächeninhalte aller Rechtecke eines Histogramms stets ${\textstyle 1}$. Anders formuliert:
  $$\int _{-\infty }^{\infty }{\hat {f}}_{X}^{(k_{0},\ldots ,k_{m})}(t)dt=1$$

Anmerkungen Histogramm II

• Die Auswahl der Klassen als Intervalle macht bereits Sinn, wenn ein Merkmal nach einer Ordinalskala verteilt ist. Die Betrachtung von Klassenbreiten (und damit auch das Erstellen von Histogrammen) ist jedoch erst bei Merkmalen sinnvoll, die mindestens nach einer Intervallskala verteilt sind.

Histogramm in R

In R: Man erstellt einen Vektor ${\textstyle X}$ mit den Daten der Urliste, also z.B.
$$\color {blue}{X<-{\text{c}}(46.5,45.3,65.4,48.0,51.2,29.0,51.5,42.1,66.5,49.6,39.2,32.7,}$$ $$\color {blue}{45.5,61.4,24.9,58.2,7.3,36.3,51.4,43.8)}$$
sowie einen Vektor mit den Intervallgrenzen, also z.B.
$$\color {blue}{{\text{grenzen}}<-{\text{c}}(0,30,50,60,80)}$$
und kann dann mit
$$\color {blue}{hist(x,breaks=grenzen,freq=FALSE)}$$
ein Histogramm erstellen.

Aufgabe Histogramm

Zur Bestimmung des Reproduktionsverhaltens unter Stress werden die Nachkommen einer Daphnienzucht gewogen. Man erhält folgende Urliste (in mg):
${\textstyle 4.56,\quad 5.01,\quad 3.94,\quad 4.67,\quad 6.74,\quad 4.73,\quad 4.97,\quad 4.73,\quad 6.95,\quad 3.74,\quad 6.94,}$
${\textstyle 4.32,\quad 3.97,\quad 4.91,\quad 5.22,\quad 4.16,\quad 5.26,\quad 3.19,\quad 3.78,\quad 2.61,\quad 4.43,\quad 4.63,}$
${\textstyle 6.22,\quad 2.69,\quad 5.57,\quad 4.07,\quad 6.16,\quad 5.46,\quad 5.61,\quad 4.12,\quad 4.42,\quad 4.86,\quad 5.43,}$
${\textstyle 6.56,\quad 4.47,\quad 5.24,\quad 7.73,\quad 7.16,\quad 2.32,\quad 6.56,\quad 6.63,\quad 6.24,\quad 2.94,\quad 5.43,}$
${\textstyle 5.19,\quad 4.41,\quad 4.27,\quad 6.86,\quad 4.96,\quad 6.54}$

Aufgabe Histogramm Fortsetzung

1. Berechnen Sie die absoluten und relativen Häufigkeiten zu der durch die folgenden Grenzen ergebenden Klassierung: $$k_{0}=0,\quad k_{1}=1,\quad k_{2}=2,\quad \ldots ,\quad k_{10}=10\quad {\text{(in mg)}}$$ Berechnen Sie dann auch die Häufigkeitsdichten und erstellen Sie ein Histogramm.
2. Verfahren Sie analog für die (gröbere) Klasseneinteilung mit den Grenzen $$k_{0}=0,\quad k_{1}=4,\quad k_{2}=5,\quad k_{3}=7,\quad k_{4}=10$$

.

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Darstellung%20eindimensionaler%20Merkmale
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.