Hilfsmittel: Punkt- und Intervallschätzung bei stetigen ZV
[Bearbeiten]In der Praxis ist die W-Dichte einer stetigen ZV  (analog zur Wahrscheinlichkeitsverteilung einer endlichen ZV) meist nicht bekannt. Manchmal können jedoch bestimmte Annahmen sinnvoll sein, wie etwa, welcher Verteilung
(analog zur Wahrscheinlichkeitsverteilung einer endlichen ZV) meist nicht bekannt. Manchmal können jedoch bestimmte Annahmen sinnvoll sein, wie etwa, welcher Verteilung  (näherungsweise) genügt.
(näherungsweise) genügt.
Informationen über  liegen meist in Form einer Stichprobe von
liegen meist in Form einer Stichprobe von  unabhängig und unter gleichen Bedingungen erhaltenen Realisationen
unabhängig und unter gleichen Bedingungen erhaltenen Realisationen  vor. Anhand dieser Daten kann man nun interessierende Kennwerte der ZV
vor. Anhand dieser Daten kann man nun interessierende Kennwerte der ZV  schätzen.
schätzen.
ZV  mit unbekannter W-Dichte
mit unbekannter W-Dichte  Daten
Daten 
 Schätzung für unbekannte Parameter der ZV
Schätzung für unbekannte Parameter der ZV
Punktschätzungen - Schätzung für EW und Varianz
[Bearbeiten]Sei  eine beliebige (diskrete oder stetige) ZV. Dabei sind der EW
eine beliebige (diskrete oder stetige) ZV. Dabei sind der EW  und die Varianz
und die Varianz  von
von  unbekannt.
unbekannt.
 wird geschätzt durch:
wird geschätzt durch:  (arithmetischer Mittelwert)
(arithmetischer Mittelwert) wird geschätzt durch:
wird geschätzt durch: 
(empirische Varianz oder korrigierte Stichprobenvarianz)
In R berechnet man:
 mean(x) und
mean(x) und
 var(x) oder sd(x)^2
var(x) oder sd(x)^2
Diese beiden Schätzungen sind in jedem Fall erwartungstreu und konsistent:
Die Ergebnisse der Schätzungen (also  und
und  ) sind zwar vom Zufall abhängig, der erwartete Durchschnitt der Schätzung entspricht aber dem unbekannten zu schätzenden Wert (also
) sind zwar vom Zufall abhängig, der erwartete Durchschnitt der Schätzung entspricht aber dem unbekannten zu schätzenden Wert (also  bzw.
bzw.  ).
).
Präziser gesagt:
Vor Erhebung der Stichprobe können  und
und  als ZV aufgefasst werden. Dann gilt:
als ZV aufgefasst werden. Dann gilt:

Ist  sehr groß so sind die Schätzungen mit hoher Wahrscheinlichkeit nahe am wahren Wert. Also
sehr groß so sind die Schätzungen mit hoher Wahrscheinlichkeit nahe am wahren Wert. Also 

Präziser gesagt: Vor Erhebung der Stichprobe können  und
und  als ZV aufgefasst werden. Dann gilt für festes
als ZV aufgefasst werden. Dann gilt für festes  :
:

und

Wir betrachten eine normalverteilte ZV mit  und unbekanntem Erwartungswert
und unbekanntem Erwartungswert  . Dann ist der arithmetische Mittelwert
. Dann ist der arithmetische Mittelwert  (als ZV aufgefasst) zu einer Stichprobe der Länge
(als ZV aufgefasst) zu einer Stichprobe der Länge  ebenfalls normalverteilt (dies wollen wir hier nicht begründen) mit
ebenfalls normalverteilt (dies wollen wir hier nicht begründen) mit  und
und  . Daraus folgt:
. Daraus folgt:
- Falls
 ist, gilt:
ist, gilt: ![{\displaystyle {\begin{array}{lclcl}P\left(M_{n}\in [\mu -10,\mu +10]\right)&=&0.9971\\P\left(M_{n}\in [\mu -5,\mu +5]\right)&=&0.8640\\P\left(M_{n}\in [\mu -1,\mu +1]\right)&=&0.2344\\P\left(M_{n}\in [\mu -0.4,\mu +0.4]\right)&=&0.0949\\P\left(M_{n}\in [\mu -0.1,\mu +0.1]\right)&=&0.0238\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/537807630034159155bc19cacbd6d923aaee2427)
- Falls
 ist, gilt:
ist, gilt: ![{\displaystyle {\begin{array}{lclcl}P\left(M_{n}\in [\mu -10,\mu +10]\right)&\approx &1\\P\left(M_{n}\in [\mu -5,\mu +5]\right)&\approx &1\\P\left(M_{n}\in [\mu -1,\mu +1]\right)&=&0.5858\\P\left(M_{n}\in [\mu -0.4,\mu +0.4]\right)&=&0.2560\\P\left(M_{n}\in [\mu -0.1,\mu +0.1]\right)&=&0.0651\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2997e5df2d314b0531ddb10281f15b4326372f5)
- Falls
 ist, gilt:
ist, gilt: ![{\displaystyle {\begin{array}{lclcl}P\left(M_{n}\in [\mu -10,\mu +10]\right)&\approx &1\\P\left(M_{n}\in [\mu -5,\mu +5]\right)&\approx &1\\P\left(M_{n}\in [\mu -1,\mu +1]\right)&=&0.9791\\P\left(M_{n}\in [\mu -0.4,\mu +0.4]\right)&=&0.6444\\P\left(M_{n}\in [\mu -0.1,\mu +0.1]\right)&=&0.1826\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dfd585c7b1855d187fa6f49f04ba313446615bc)
Ziel ist es nun, auch Intervallschätzungen für unbekannte Parameter von stetigen ZV anzugeben. Dazu benötigen wir Kenntnisse über einige weitere Verteilungen ( -Verteilung und
-Verteilung und  -Verteilung), die üblicherweise nicht direkt als Modell für ein ZE verwendet werden. Sie treten aber bespielsweise auf, wenn man stetige ZV auf geeignete Art und Weise verknüpft und werden daher bei der Berechnung von Konfidenzintervallen für die Parameter dieser Verteilungen benötigt.
-Verteilung), die üblicherweise nicht direkt als Modell für ein ZE verwendet werden. Sie treten aber bespielsweise auf, wenn man stetige ZV auf geeignete Art und Weise verknüpft und werden daher bei der Berechnung von Konfidenzintervallen für die Parameter dieser Verteilungen benötigt.
In diesem Abschnitt wollen wir diese Verteilungen definieren und ihre wichtigsten Eigenschaften zusammenfassen. Als weiteres Hilfsmittel brauchen wir dazu die Gamma-Funktion.
Die Gamma-Funktion ist definiert durch: 
In R berechnet man  für
für  durch gamma(x).
durch gamma(x).
Werte der Gamma-Funktion auf den ganzen und halben Zahlen
[Bearbeiten]- Für alle
 gilt:
gilt: 
- Für alle
 gilt:
gilt: 
Es gilt:

Sei  gegeben.
gegeben.
Eine ZV  mit der W-Dichte
mit der W-Dichte 
heißt  -verteilt mit
-verteilt mit  Freiheitsgraden (FG).
Freiheitsgraden (FG).
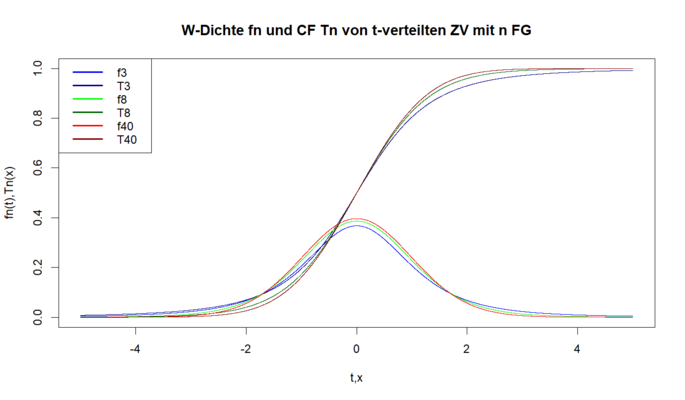
Verteilungsfunktion einer t-Verteilung
[Bearbeiten]Die Verteilungsfunktion einer  -verteilten ZV mit
-verteilten ZV mit  FG bezeichnen wir mit
FG bezeichnen wir mit  :
: 
Interaktive Shiny-App zur t-Verteilung:
Download und Link
Für große  nähert sich die
nähert sich die  -Verteilung einer Standardnormalverteilung an (also
-Verteilung einer Standardnormalverteilung an (also  für große
für große  ).
).
Für eine  -verteilte ZV
-verteilte ZV  mit
mit  FG berechnet man in
R:
FG berechnet man in
R:
- die Funktionswerte der W-Dichte von
 durch:
durch: 
- die Funktionswerte der VF von
 durch:
durch: 
- die Wahrscheinlichkeit für
![{\textstyle X\in [u,v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b49bfad24a43cfec5f9fb8e1c198d72e1f62524) durch:
durch: 
- für
![{\textstyle q\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41c7ef054e569a84b7ebe6f2621a2480c868e389) die Zahl
die Zahl  mit
mit  durch:
durch: 
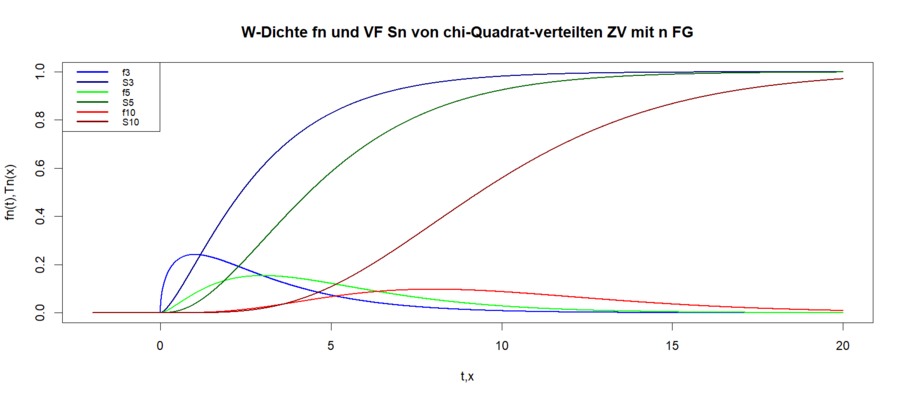
Sei  gegeben.
gegeben.
Eine ZV  mit der W-Dichte
mit der W-Dichte

heißt Χ2 -verteilt mit  Freiheitsgraden (FG).
Freiheitsgraden (FG).
Die Verteilungsfunktion einer  -verteilten ZV mit
-verteilten ZV mit  FG bezeichnen wir mit
FG bezeichnen wir mit  :
:
Interaktive Shiny-App zur Chi-Quadrat-Verteilung:
Download und Link
Für eine  -verteilte ZV
-verteilte ZV  mit
mit  FG berechnet man in R:
FG berechnet man in R:
- die Funktionswerte der W-Dichte von
 durch:
durch: 
- die Funktionswerte der VF von
 durch:
durch: 
- die Wahrscheinlichkeit für
![{\textstyle X\in [u,v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b49bfad24a43cfec5f9fb8e1c198d72e1f62524) durch:
durch: 
- für
![{\textstyle q\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41c7ef054e569a84b7ebe6f2621a2480c868e389) die Zahl
die Zahl  mit
mit  durch:
durch: 
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.





























![{\displaystyle {\begin{array}{lclcl}P\left(M_{n}\in [\mu -10,\mu +10]\right)&=&0.9971\\P\left(M_{n}\in [\mu -5,\mu +5]\right)&=&0.8640\\P\left(M_{n}\in [\mu -1,\mu +1]\right)&=&0.2344\\P\left(M_{n}\in [\mu -0.4,\mu +0.4]\right)&=&0.0949\\P\left(M_{n}\in [\mu -0.1,\mu +0.1]\right)&=&0.0238\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/537807630034159155bc19cacbd6d923aaee2427)

![{\displaystyle {\begin{array}{lclcl}P\left(M_{n}\in [\mu -10,\mu +10]\right)&\approx &1\\P\left(M_{n}\in [\mu -5,\mu +5]\right)&\approx &1\\P\left(M_{n}\in [\mu -1,\mu +1]\right)&=&0.5858\\P\left(M_{n}\in [\mu -0.4,\mu +0.4]\right)&=&0.2560\\P\left(M_{n}\in [\mu -0.1,\mu +0.1]\right)&=&0.0651\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2997e5df2d314b0531ddb10281f15b4326372f5)

![{\displaystyle {\begin{array}{lclcl}P\left(M_{n}\in [\mu -10,\mu +10]\right)&\approx &1\\P\left(M_{n}\in [\mu -5,\mu +5]\right)&\approx &1\\P\left(M_{n}\in [\mu -1,\mu +1]\right)&=&0.9791\\P\left(M_{n}\in [\mu -0.4,\mu +0.4]\right)&=&0.6444\\P\left(M_{n}\in [\mu -0.1,\mu +0.1]\right)&=&0.1826\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dfd585c7b1855d187fa6f49f04ba313446615bc)




















![{\textstyle X\in [u,v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b49bfad24a43cfec5f9fb8e1c198d72e1f62524)

![{\textstyle q\in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41c7ef054e569a84b7ebe6f2621a2480c868e389)