In einer Menge von  Objekten sind
Objekten sind  Objekte mit einer bestimmten Eigenschaft ausgezeichnet. Nun werden daraus
Objekte mit einer bestimmten Eigenschaft ausgezeichnet. Nun werden daraus  Objekte zufällig ausgewählt (gezogen). Wichtig ist dabei, dass die Ziehung zufällig und unabhängig von der Eigenschaft ist, d.h. die ausgezeichneten Objekte haben dieselbe Chance gezogen zu werden, wie die anderen Objekte.
Objekte zufällig ausgewählt (gezogen). Wichtig ist dabei, dass die Ziehung zufällig und unabhängig von der Eigenschaft ist, d.h. die ausgezeichneten Objekte haben dieselbe Chance gezogen zu werden, wie die anderen Objekte.
Die ZV  beschreibt die Zahl
beschreibt die Zahl  der ausgezeichneten Objekte unter den Gezogenen.
der ausgezeichneten Objekte unter den Gezogenen.
Man sagt:  ist hypergeometrisch verteilt mit
ist hypergeometrisch verteilt mit  Ausgezeichneten bei
Ausgezeichneten bei  Objekten insgesamt (bzw. mit
Objekten insgesamt (bzw. mit  Nicht-Ausgezeichneten) und
Nicht-Ausgezeichneten) und  Gezogenen.
Gezogenen.
Die möglichen Werte von  sind dann
sind dann  und es gilt:
und es gilt: 
Für  und
und  ist beispielsweise:
ist beispielsweise:

Für  ist:
ist:

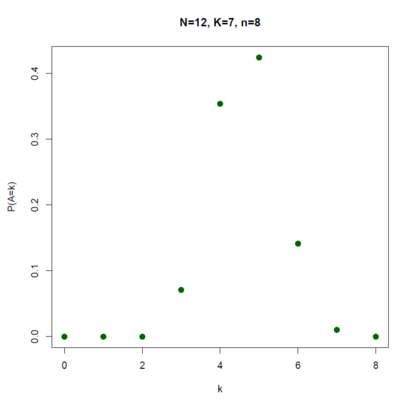
Hier einige weitere Beispiele:
Interaktive Shiny-App zur Hypergeometrischen Verteilung:
Download und Link
Es folgt:



Für  und
und  ist beispielsweise:
ist beispielsweise:

In R:

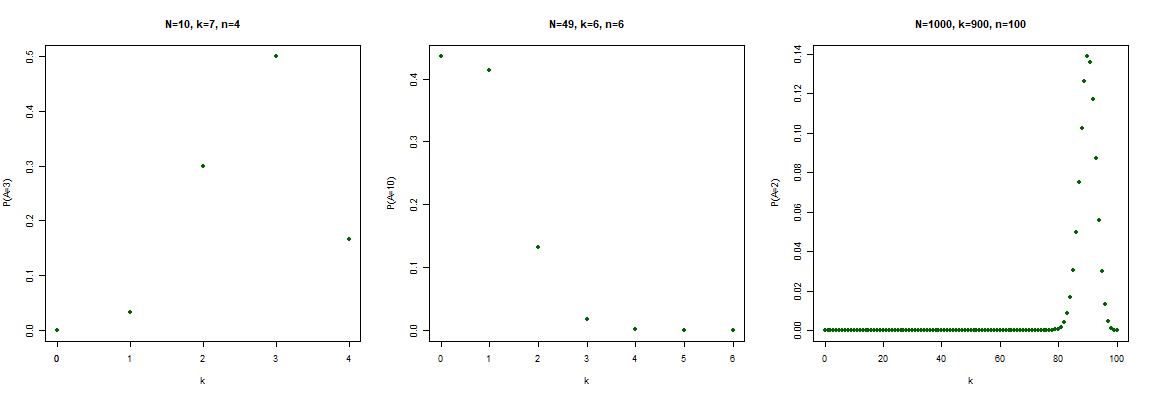
Berechnen Sie für eine hypergeometrisch verteilte ZV  mit den jeweils angegebenen Werten für
mit den jeweils angegebenen Werten für  und
und  die angegebenen Wahrscheinlichkeiten:
die angegebenen Wahrscheinlichkeiten:
- Für
 und
und  :
:  für alle
für alle 
- Für
 und
und  :
: 
- Für
 und
und  :
: 
- (Ziehen ohne Zurücklegen) Aus einer Lostrommel, die
 Kugeln enthält, von denen
Kugeln enthält, von denen  rot sind, werden ohne Zurücklegen
rot sind, werden ohne Zurücklegen  Kugeln gezogen. Die ZV für die Anzahl der roten Kugeln unter den Gezogenen ist hypergeometrisch verteilt.
Kugeln gezogen. Die ZV für die Anzahl der roten Kugeln unter den Gezogenen ist hypergeometrisch verteilt.
- In einem Teich befinden sich
 Fische einer Art, von denen
Fische einer Art, von denen  markiert sind. Nun werden
markiert sind. Nun werden  Fische gefangen. Die ZV für die Zahl der markierten Fische unter den Gefangenen ist hypergeometrisch verteilt mit
Fische gefangen. Die ZV für die Zahl der markierten Fische unter den Gefangenen ist hypergeometrisch verteilt mit  und
und  . (Voraussetzung: Die markierten Fische sind über den See gleichmäßig verteilt und lassen sich genauso leicht fangen, wie die Übrigen.)
. (Voraussetzung: Die markierten Fische sind über den See gleichmäßig verteilt und lassen sich genauso leicht fangen, wie die Übrigen.)
- In einer Klasse befinden sich
 Jungen und
Jungen und  Mädchen. Es werden
Mädchen. Es werden  Schüler/innen für ein Projekt ausgelost. Die ZV, die die Zahl der Jungen unter den Ausgelosten angibt, ist hypergeometrisch verteilt mit
Schüler/innen für ein Projekt ausgelost. Die ZV, die die Zahl der Jungen unter den Ausgelosten angibt, ist hypergeometrisch verteilt mit  und
und  .
.
Wie groß ist beim Lotto (6 aus 49) die Wahrscheinlichkeit, genau  Richtige zu haben (
Richtige zu haben ( ).
).
Bei einem Multiple-Choice Test gibt es 20 Aussagen, von denen genau 10 richtig sind. Ein unvorbereiteter Teilnehmer kreuzt willkürlich genau 10 Aussagen an. Wie groß ist die Wahrscheinlichkeit, dass dabei  der angekreuzten Aussagen richtig sind?
der angekreuzten Aussagen richtig sind?
Unter 500 Glühbirnen in einem Karton befinden sich 35 defekte. Bei einer Qualitätskontrolle werden 50 Birnen getestet. Wie groß ist die Wahrscheinlichkeit, dass
ist die Wahrscheinlichkeit, dass  der Birnen defekt ist?
der Birnen defekt ist?
Für eine hypergeometrisch verteilte ZV  mit
mit  wie bisher gilt:
wie bisher gilt:

Für  und
und  haben wir oben bereits die Wahrscheinlichkeitsverteilung bestimmt. Daraus ergibt sich:
haben wir oben bereits die Wahrscheinlichkeitsverteilung bestimmt. Daraus ergibt sich: 
Für  und
und  berechnen wir zunächst
berechnen wir zunächst

für alle möglichen Werte  :
:

Daraus ergibt sich:

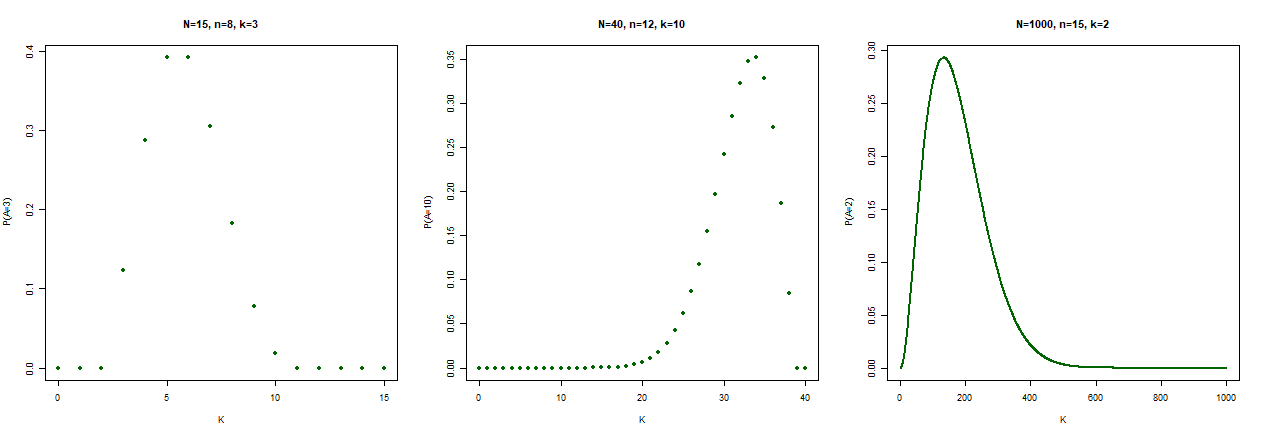
Bestimmen Sie für eine hypergeometrsich verteilte ZV  mit
mit  ,
,  und
und  die nachfolgenden Werte:
die nachfolgenden Werte:
-

-

-

-

Bestimmen Sie Erwartungswert und Varianz.
Wenn für die Vorlesung 79 Menschen angemeldet sind, von denen ca. 30 Personen auch regelmäßig in die Vorlesung kommen. Die Klausur wird von 40 Personen geschrieben. Wie hoch ist die Wahrscheinlichkeit, dass
- alle 30 Personen aus der Vorlesung die Klausur mitschreiben?
- mindestens 20 Personen aus der Vorlesung die Klausur mitschreiben?
- maximal 20 Personen aus der Vorlesung die Klausur mitschreiben?
Bestimmen Sie auch Erwartungswert und Varianz.
Schätzung der Zahl der ausgezeichneten Objekte K
[Bearbeiten]
Von  Glübirnen einer Lieferung sind eine unbekannte Anzahl
Glübirnen einer Lieferung sind eine unbekannte Anzahl  defekt. Man testet
defekt. Man testet  zufällig ausgewählte Birnen und stellt fest, dass
zufällig ausgewählte Birnen und stellt fest, dass  davon defekt sind. Wie kann man daraus auf die Zahl
davon defekt sind. Wie kann man daraus auf die Zahl  schließen?
schließen?
Situation:

Genauer:
 und
und  sind feststehend und bekannt. Oft kann man
sind feststehend und bekannt. Oft kann man  selbst festlegen.
selbst festlegen. entsteht zufällig, ist dann aber bekannt.
entsteht zufällig, ist dann aber bekannt. steht fest, ist aber nicht bekannt.
steht fest, ist aber nicht bekannt.
 Wiederum ist dabei folglich die Schätzung zufällig.
Wiederum ist dabei folglich die Schätzung zufällig.
Erwartungstreue Punktschätzungen für K
[Bearbeiten]Durch  erhält man eine erwartungstreue Schätzung für
erhält man eine erwartungstreue Schätzung für  .
.
Genauer: Die Zahl  hängt vom Zufall ab und wird (vor der Datenerhebung) durch die ZV
hängt vom Zufall ab und wird (vor der Datenerhebung) durch die ZV  beschrieben. Da die Schätzung für (die feste aber unbekannte Zahl)
beschrieben. Da die Schätzung für (die feste aber unbekannte Zahl)  von
von  abhängt, ist sie ebenfalls vom Zufall abhängig. Die Schätzung
abhängt, ist sie ebenfalls vom Zufall abhängig. Die Schätzung  kann somit als ZV beschrieben werden. Dabei gilt dann (unabhängig vom unbekannten Wert
kann somit als ZV beschrieben werden. Dabei gilt dann (unabhängig vom unbekannten Wert
 ) stets
) stets  .
.

Mit der Maximum-Likelihood-Methode wird  (basierend auf der zufälligen Zahl
(basierend auf der zufälligen Zahl  ) so geschätzt, dass die Wahrscheinlichkeit
) so geschätzt, dass die Wahrscheinlichkeit  maximal wird. Wir suchen also die Maximumstelle der Likelihood-Funktion
maximal wird. Wir suchen also die Maximumstelle der Likelihood-Funktion
![{\displaystyle L:\{0,\ldots ,N\}\to [0,1],\ L(K)={\frac {{K \choose k}\cdot {N-K \choose n-k}}{N \choose n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48e720c4775594fe6c70b66d390499c7c750240b)
Man stellt fest:
Die Maximumstelle(n) von  ist/sind:
ist/sind:

(dabei bezeichnet  die größte ganze Zahl, die kleiner oder gleich
die größte ganze Zahl, die kleiner oder gleich  ist)
ist)
 und
und 


Gib eine Methode an, mit der man aus  ein Intervall
ein Intervall ![{\textstyle [K_{U},K_{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9992ea17c09c32b849669b00f6a380ed85f7d84) bestimmen kann, so dass die Wahrscheinlichkeit, dass sich ein Intervall ergibt, das
bestimmen kann, so dass die Wahrscheinlichkeit, dass sich ein Intervall ergibt, das  enthält, garantiert (also für jeden denkbaren Wert von
enthält, garantiert (also für jeden denkbaren Wert von  ) größer oder gleich einem vorgegebenen Konfidenzniveau
) größer oder gleich einem vorgegebenen Konfidenzniveau  ist.
ist.

![{\displaystyle {\stackrel {\text{methodisch}}{\longrightarrow }}{\text{(Intervall-)Schätzung }}[K_{U},K_{O}]{\text{ für }}K}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2604a506cf5837eb0603101f2f9f50b1f3e2c2b2)
![{\displaystyle {\textbf {Ziel:}}{\text{ Für jeden möglichen Wert von }}K:\quad P\left([K_{U},K_{O}]\ni K\right)\geq \delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/77154a2e5c6b71a5f6c0c5e257aecaf4e49fe593) Eine sinnvolle Möglichkeit wird im Folgenden beschrieben:
Eine sinnvolle Möglichkeit wird im Folgenden beschrieben:
IVS für K, die ein gegebenes Konfidenzniveau einhält
[Bearbeiten]Gegeben seien  und
und  . Unbekannt sei
. Unbekannt sei  . Weiter sei ein Konfidenzniveau
. Weiter sei ein Konfidenzniveau ![{\textstyle \delta \in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0e6172b1124969f7a4158fa7792a3bfb3944a7b) vorgegeben.
vorgegeben.
Basierend auf der zufälligen Zahl  geht man nun wie folgt vor:
geht man nun wie folgt vor:
- Man bestimmt
 als die kleinstmögliche Zahl mit
als die kleinstmögliche Zahl mit 

- Man bestimmt
 als die größtmögliche Zahl mit
als die größtmögliche Zahl mit 

Ohne weiter in die mathematischen Hintergründe einzusteigen, halten wir fest, dass die folgende (bei Intervallschätzungen immer zu erreichende) Bedingung bei diesem Verfahren garantiert erfüllt ist:
![{\displaystyle P\left([K_{U},K_{O}]\ni K\right)\geq \delta \quad {\text{(D.h. das Konfidenzniveau }}\delta {\text{ wird eingehalten.)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3ff451bd7289823ab6909bea50e7bd0b677af92)
Man beachte, dass der Aussage "![{\textstyle K\in [K_{U},K_{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4e8da961c575e78520d1c98a9db2a3068b897e9)
 " eine Wahrscheinlichkeit zugeschrieben werden kann, weil die Intervallgrenzen
" eine Wahrscheinlichkeit zugeschrieben werden kann, weil die Intervallgrenzen  und
und  zufällig sind (und nicht etwa der unbekannte Wert
zufällig sind (und nicht etwa der unbekannte Wert  ).
).
Wir betrachten erneut den Fall  und führen eine Intervallschätzung zum Niveau
und führen eine Intervallschätzung zum Niveau  durch.
durch.
- Wir suchen also zunächst die kleinstmögliche Zahl
 mit
mit 

Durch Ausprobieren findet man:

- Analog suchen wir die größtmögliche Zahl mit


Durch Ausprobieren findet man: 
Damit ist ![{\textstyle [K_{U},K_{O}]=[17,402]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dae1cb44309e02425b6f4c96da27adb0bd1f2ca2) das gesuchte Konfidenzintervall zu
das gesuchte Konfidenzintervall zu  .
.
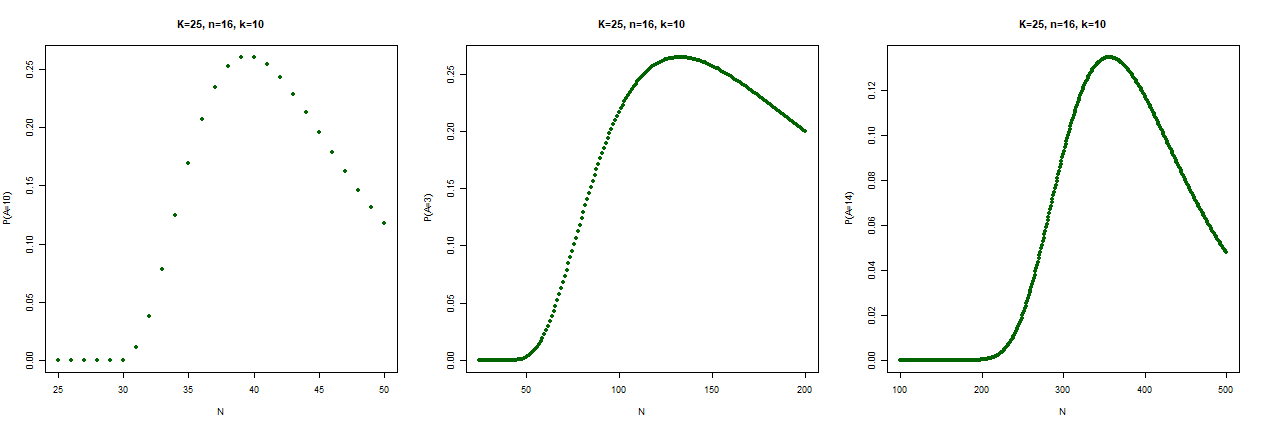
Für  und
und  berechnet man abhängig von
berechnet man abhängig von  die folgenden ML-Schätzungen und Intervallschätzungen zum Vertrauensniveau
die folgenden ML-Schätzungen und Intervallschätzungen zum Vertrauensniveau  :
:
![{\displaystyle {\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|}\hline k&0&1&2&3&4&5&6&7&8&9\\\hline {\hat {K}}&0&11&22&33&44&55&67&78&89&100\\\hline K\in &[0,19]&[2,34]&[8,47]&[16,60]&[24,72]&[33,84]&[43,95]&[52,106]&[62,117]&[73,127]\\\hline \end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da7e42e024afa035ed9c471f18db3e0e14af5007)
![{\displaystyle {\begin{array}{|c||c|c|c|c|c|c|c|c|c|}\hline k&10&11&12&13&14&15&16&17&18\\\hline {\hat {K}}&111&122&134&145&156&167&178&189&201\\\hline K\in &[83,138]&[94,148]&[105,157]&[116,167]&[128,176]&[140,184]&[153,192]&[166,198]&[181,200]\\\hline \end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5630ab812655ea64c57c21cb43f35c7d7526af9)
- Angenommen, es ist
 . Dann ist die Intervallschätzung für
. Dann ist die Intervallschätzung für  korrekt. Die Wahrscheinlichkeit dafür ist:
korrekt. Die Wahrscheinlichkeit dafür ist:

- Angenommen, es ist
 . Dann ist die Intervallschätzung für
. Dann ist die Intervallschätzung für  korrekt. Die Wahrscheinlichkeit dafür ist:
korrekt. Die Wahrscheinlichkeit dafür ist:

- Angenommen, es ist
 . Dann ist die Intervallschätzung nur für
. Dann ist die Intervallschätzung nur für  korrekt. Die Wahrscheinlichkeit dafür ist:
korrekt. Die Wahrscheinlichkeit dafür ist:

Das mathematische Modell garantiert, dass die Intervallschätzung bei beliebigem  immer mindestens mit der Wahrscheinlichkeit
immer mindestens mit der Wahrscheinlichkeit  korrekt ist.
korrekt ist.
In Ihrem Wohnort stehen  Wohngebaude. Sie wissen, dass nur Eines von Vieren einen Keller hat.
Wohngebaude. Sie wissen, dass nur Eines von Vieren einen Keller hat.
- Führen Sie für
 eine Punktschätzung durch, stellen Sie die Maximum-Likelihood-Funktion auf und plotten Sie diese in R.
eine Punktschätzung durch, stellen Sie die Maximum-Likelihood-Funktion auf und plotten Sie diese in R.
- Geben Sie die Formeln für die Intervallschätzung mit
 für
für  an.
an.
Schätzung der Gesamtzahl der Objekte N
[Bearbeiten]
In einem See befindet sich eine unbekannte Anzahl  von Fischen einer Art. Man möchte wissen, wie groß
von Fischen einer Art. Man möchte wissen, wie groß  in etwa ist. Dazu fängt man eine (kleinere) Anzahl
in etwa ist. Dazu fängt man eine (kleinere) Anzahl  von Fischen und markiert sie. Dann setzt man sie wieder aus und wartet einen angemessenen Zeitraum. Dann fängt man in einem zweiten Fischzug
von Fischen und markiert sie. Dann setzt man sie wieder aus und wartet einen angemessenen Zeitraum. Dann fängt man in einem zweiten Fischzug  Fische und bestimmt die Anzahl
Fische und bestimmt die Anzahl  der markierten Fische unter ihnen.
der markierten Fische unter ihnen.
Beispielsweise hat man  Fische markiert und unter
Fische markiert und unter  gefangenen Fischen
gefangenen Fischen  markierte Fische wiedergefunden.
markierte Fische wiedergefunden.
Wie kann man daraus eine sinnvolle Schätzung für  abgeben?
abgeben?
Situation:
 Genauer:
Genauer:
 und
und  sind fest und bekannt. Manchmal kann man
sind fest und bekannt. Manchmal kann man  und
und  selbst festlegen.
selbst festlegen. entsteht zufällig, ist dann aber bekannt.
entsteht zufällig, ist dann aber bekannt. mit
mit  steht fest, ist aber nicht bekannt.
steht fest, ist aber nicht bekannt.
 Wiederum ist damit die Schätzung zufällig.
Wiederum ist damit die Schätzung zufällig.
Erwartungstreue Punktschätzungen für N
[Bearbeiten]Durch  erhält man eine Schätzung für
erhält man eine Schätzung für  .
.
Dabei gilt:  ist erwartungstreu für
ist erwartungstreu für  .
.
Genauer: Die Zahl  hängt vom Zufall ab und wird (vor der Datenerhebung) durch die ZV
hängt vom Zufall ab und wird (vor der Datenerhebung) durch die ZV  beschrieben. Da die Schätzung für (die feste aber unbekannte Zahl)
beschrieben. Da die Schätzung für (die feste aber unbekannte Zahl)  von
von  abhängt, ist sie ebenfalls vom Zufall abhängig. Die Schätzung
abhängt, ist sie ebenfalls vom Zufall abhängig. Die Schätzung  kann somit als ZV beschrieben werden. Dabei gilt dann (unabhängig vom unbekannten Wert
kann somit als ZV beschrieben werden. Dabei gilt dann (unabhängig vom unbekannten Wert  ) stets
) stets  .
.

Schätzung für N mit der Maximum-Likelihood-Methode
[Bearbeiten]Mit der Maximum-Likelihood-Methode wird  (basierend auf der zufälligen Zahl
(basierend auf der zufälligen Zahl  ) so geschätzt, dass die Wahrscheinlichkeit
) so geschätzt, dass die Wahrscheinlichkeit  maximal wird. Wir suchen also die Maximumstelle der Likelihood-Funktion
maximal wird. Wir suchen also die Maximumstelle der Likelihood-Funktion
![{\displaystyle L:\{\max(K,n),\ldots \}\to [0,1],\ L(N)={\frac {{K \choose k}\cdot {N-K \choose n-k}}{N \choose n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/076638b4879d2a28bafd8696f84bc001cb219bb6)
Man stellt fest:
Die Maximumstelle(n) ist/sind von  :
:  (dabei bezeichnet
(dabei bezeichnet  die größte ganze Zahl, die kleiner oder gleich
die größte ganze Zahl, die kleiner oder gleich  ist)
ist)



Gib eine Methode an, mit der man aus  ein Intervall
ein Intervall ![{\textstyle [N_{U},N_{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00e660add57c9c93d8daef3f33b0234fc4289993) bestimmen kann, so dass die Wahrscheinlichkeit, dass sich ein Intervall ergibt, das
bestimmen kann, so dass die Wahrscheinlichkeit, dass sich ein Intervall ergibt, das  enthält, auf jeden Fall (also für jeden denkbaren Wert von
enthält, auf jeden Fall (also für jeden denkbaren Wert von  ) mindestens ein vorgegebenes Konfidenzniveau
) mindestens ein vorgegebenes Konfidenzniveau  ist.
ist.

![{\displaystyle {\stackrel {\text{methodisch}}{\longrightarrow }}{\text{(Intervall-)Schätzung }}[N_{U},N_{O}]{\text{ für }}N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ac6e980ff9a8de29dee31a69714d1008337f1a1)
![{\displaystyle {\textbf {Ziel:}}{\text{ Für jeden möglichen Wert von }}N:\quad P\left([N_{U},N_{O}]\ni N\right)\geq \delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d513a9dd206aedca9032d28827722d416e272c)
Eine sinnvolle Möglichkeit wird im Folgenden beschrieben.
IVS für N, die ein gegebenes Konfidenzniveau einhält
[Bearbeiten]Gegeben seien  . Unbekannt sei
. Unbekannt sei  . Weiter sei ein Konfidenzniveau
. Weiter sei ein Konfidenzniveau ![{\textstyle \delta \in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0e6172b1124969f7a4158fa7792a3bfb3944a7b) vorgegeben.
vorgegeben.
Basierend auf der zufälligen Zahl  geht man nun wie folgt vor:
geht man nun wie folgt vor:
- Man bestimmt
 als die kleinstmögliche Zahl mit
als die kleinstmögliche Zahl mit


- Man bestimmt
 als die größtmögliche Zahl mit
als die größtmögliche Zahl mit


Wir halten fest, dass die folgende (bei Intervallschätzungen immer zu erreichende) Bedingung bei diesem Verfahren garantiert erfüllt ist: ![{\displaystyle P\left([N_{U},N_{O}]\ni N\right)\geq \delta \quad {\text{(D.h. das Konfidenzniveau }}\delta {\text{ wird eingehalten.)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4289fd03bbc81f836dc7c78b69a7c209ad9fa0b8) Man beachte, dass der Aussage "
Man beachte, dass der Aussage "![{\textstyle N\in [N_{U},N_{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6c993f8785429ffba929aba71fcb2db411d96c1) "
" eine Wahrscheinlichkeit zugeschrieben werden kann, weil die Intervallgrenzen
eine Wahrscheinlichkeit zugeschrieben werden kann, weil die Intervallgrenzen  und
und  zufällig sind (und nicht etwa der unbekannte Wert
zufällig sind (und nicht etwa der unbekannte Wert  ).
).
Wir betrachten erneut den Fall  und führen eine Intervallschätzung zum Niveau
und führen eine Intervallschätzung zum Niveau  durch.
durch.
- Wir suchen also zunächst die kleinstmögliche Zahl
 mit
mit 
 Durch Ausprobieren findet man:
Durch Ausprobieren findet man: 
- Analog suchen wir die größtmögliche Zahl mit

 Durch Ausprobieren findet man:
Durch Ausprobieren findet man: 
Damit ist ![{\textstyle [N_{U},N_{O}]=[272,499]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd18192deb37367b81b5b87a132024aef672945b) das gesuchte Konfidenzintervall zu
das gesuchte Konfidenzintervall zu  .
.
Einige Zeit nach einem Wiederansiedlungsversuch einer Spezies wollen Sie wissen, ob dieser geglückt ist und die Spezies sich vermehrt hat.
- Geben Sie an, wie Sie zur Überprüfung vorgehen würden (Sie können nicht alle Exemplare zählen).
- Seien nun
 . Bestimmen Sie
. Bestimmen Sie  mittels der einfachen Punktschätzung, stellen Sie die Maximum-Likelihood-Funktion auf, plotten diese in R und führen eine Intervallschätzung mit
mittels der einfachen Punktschätzung, stellen Sie die Maximum-Likelihood-Funktion auf, plotten diese in R und führen eine Intervallschätzung mit  durch.
durch.
- Was fällt Ihnen hinsichtlich der verschiedenen Schätzungen auf? Vergleichen Sie Ihre Ergebnisse.
Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.















































































![{\displaystyle L:\{0,\ldots ,N\}\to [0,1],\ L(K)={\frac {{K \choose k}\cdot {N-K \choose n-k}}{N \choose n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48e720c4775594fe6c70b66d390499c7c750240b)








![{\textstyle [K_{U},K_{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d9992ea17c09c32b849669b00f6a380ed85f7d84)


![{\displaystyle {\stackrel {\text{methodisch}}{\longrightarrow }}{\text{(Intervall-)Schätzung }}[K_{U},K_{O}]{\text{ für }}K}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2604a506cf5837eb0603101f2f9f50b1f3e2c2b2)
![{\displaystyle {\textbf {Ziel:}}{\text{ Für jeden möglichen Wert von }}K:\quad P\left([K_{U},K_{O}]\ni K\right)\geq \delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/77154a2e5c6b71a5f6c0c5e257aecaf4e49fe593)

![{\textstyle \delta \in ]0,1[}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0e6172b1124969f7a4158fa7792a3bfb3944a7b)






![{\displaystyle P\left([K_{U},K_{O}]\ni K\right)\geq \delta \quad {\text{(D.h. das Konfidenzniveau }}\delta {\text{ wird eingehalten.)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d3ff451bd7289823ab6909bea50e7bd0b677af92)
![{\textstyle K\in [K_{U},K_{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4e8da961c575e78520d1c98a9db2a3068b897e9)








![{\textstyle [K_{U},K_{O}]=[17,402]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dae1cb44309e02425b6f4c96da27adb0bd1f2ca2)



![{\displaystyle {\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|}\hline k&0&1&2&3&4&5&6&7&8&9\\\hline {\hat {K}}&0&11&22&33&44&55&67&78&89&100\\\hline K\in &[0,19]&[2,34]&[8,47]&[16,60]&[24,72]&[33,84]&[43,95]&[52,106]&[62,117]&[73,127]\\\hline \end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da7e42e024afa035ed9c471f18db3e0e14af5007)
![{\displaystyle {\begin{array}{|c||c|c|c|c|c|c|c|c|c|}\hline k&10&11&12&13&14&15&16&17&18\\\hline {\hat {K}}&111&122&134&145&156&167&178&189&201\\\hline K\in &[83,138]&[94,148]&[105,157]&[116,167]&[128,176]&[140,184]&[153,192]&[166,198]&[181,200]\\\hline \end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5630ab812655ea64c57c21cb43f35c7d7526af9)


























![{\displaystyle L:\{\max(K,n),\ldots \}\to [0,1],\ L(N)={\frac {{K \choose k}\cdot {N-K \choose n-k}}{N \choose n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/076638b4879d2a28bafd8696f84bc001cb219bb6)




![{\textstyle [N_{U},N_{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00e660add57c9c93d8daef3f33b0234fc4289993)

![{\displaystyle {\stackrel {\text{methodisch}}{\longrightarrow }}{\text{(Intervall-)Schätzung }}[N_{U},N_{O}]{\text{ für }}N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ac6e980ff9a8de29dee31a69714d1008337f1a1)
![{\displaystyle {\textbf {Ziel:}}{\text{ Für jeden möglichen Wert von }}N:\quad P\left([N_{U},N_{O}]\ni N\right)\geq \delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/80d513a9dd206aedca9032d28827722d416e272c)








![{\displaystyle P\left([N_{U},N_{O}]\ni N\right)\geq \delta \quad {\text{(D.h. das Konfidenzniveau }}\delta {\text{ wird eingehalten.)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4289fd03bbc81f836dc7c78b69a7c209ad9fa0b8)
![{\textstyle N\in [N_{U},N_{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6c993f8785429ffba929aba71fcb2db411d96c1)








![{\textstyle [N_{U},N_{O}]=[272,499]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd18192deb37367b81b5b87a132024aef672945b)
