Kurs:Statistik für Anwender/Kurzvorstellung weiterer Hypothesentests
Kurzvorstellung weiterer Tests
[Bearbeiten]Beispiele siehe R-Skript unter GitHub.
In diesem Kapitel sollen einige weitere Tests vorgestellt werden, die für gewisse Anwendungen relevant sind. Auf die konkrete (meist kompliziertere) Durchführung (d.h. Berechnung der Testsstatistik und des p-Werts) gehen wir nur kurz oder gar nicht ein. Unverzichtbar ist jedoch das Verständnis der zum jeweiligen Test gehörenden Nullhypothese.
Der Kolmogoroff-Smirnov-Test
[Bearbeiten]Einstichprobenfall
[Bearbeiten]Situation, Nullhypothese und Daten
[Bearbeiten]Situation: Gegeben sei eine beliebige stetige ZV .
Nullhypothese: ist nach verteilt (Anpassungstest)
mit einer hypothetischen (genau festgelegten) stetigen Verteilung mit Verteilungsfunktion
Benötigte Daten: Stichprobe
Teststatistik I
[Bearbeiten]Teststatistik: Man bestimmt zunächst (in Abhängigkeit von ) die relative Häufigkeit der , die sind, also
heißt empirische Verteilungsfunktion der Stichprobe
und (zum Vergleich) die Wahrscheinlichkeit, dass ist (falls gilt), also
Teststatistik II
[Bearbeiten]Die Teststatistik berechnet sich als die maximale Abweichung zwischen beiden Werten, also
Falls gilt, erwartet man nur eine geringe Abweichung zwischen den relativen Häufigkeiten und den entsprechenden Wahrscheinlichkeiten. Damit spricht ein hoher Wert von gegen .
p-Wert
[Bearbeiten]-Wert: Die Berechnung des p-Werts aus der Teststatistik ist kompliziert, hängt aber nicht von (sondern nur von ) ab. Man kann den -Wert mit Hilfe von Tabellen (für kleine ) oder Näherungsformeln (für große ) bestimmen. Wir wollen hier aber nicht näher auf die Berechnung eingehen.
Durchführung in R
[Bearbeiten]Durchführung in R: mit dem Befehl ks.test: Einlesen der Stichprobe in einen Vektor und dann beispielsweise
falls eine Normalverteilung (mit gegebenem EW und gegebener SA ) ist
falls eine Exponentialverteilung mit (gegebenem Parameter ) ist
falls eine Gleichverteilung auf ist ( und gegeben)
falls eine Binomialverteilung mit gegebenem EW und gegebener SA ist
Beispiel 1.1
[Bearbeiten]Man testet die Nullhypothese
anhand der folgenden Stichprobe :
Beispiel 1.2
[Bearbeiten]
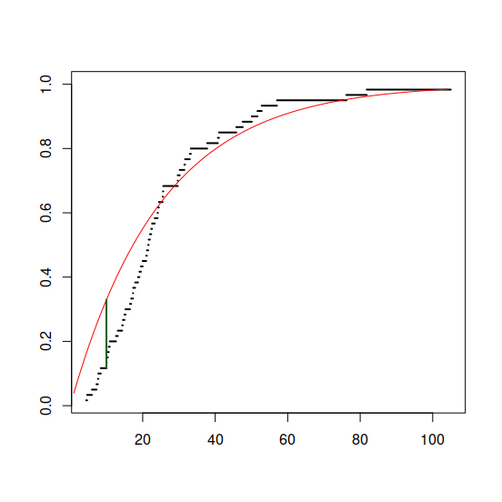
Damit erstellt man nun einen Plot der empirischen Verteilungsfunktion zu dieser Stichprobe (schwarz) und zum Vergleich die hypothetische Verteilungsfunktion (rot) falls gilt, also:
(vergleiche die Verteilungsfunktion einer exponentialverteilten ZV)
Beispiel 1.3
[Bearbeiten]Beispiel 1.4
[Bearbeiten]Die Teststatistik ergibt sich als maximaler (vertikaler) Abstand der beiden Funktionsgraphen, es ist (im Bild grün eingezeichnet).
In R berechnet man diese Teststatistik und den -Wert einfach mit . Mit hat man hier ein hochsignifikantes Ergebnis, es ist als davon auszugehen, dass die Daten keiner Exponentialverteilung mit entstammen.
Variante: Test auf bestimmte Verteilung I
[Bearbeiten]Man kann in manchen Fällen den KS-Test auch als Test auf eine bestimmte Verteilungsart einsetzen (z.B. Test auf Normalverteilung oder Test auf Exponentialverteilung), wobei man vor Berechnung der Teststatistik die unbekannten Parameter aus der Stichprobe schätzen muss. In diesem Fall ändert sich allerdings die Verteilung der Teststatistik. Die Berechnung des -Werts ist dann abhängig von der hypothetischen Verteilungsart und kann sehr aufwändig werden. Für bestimmte hypothetische Verteilungsarten existieren Variationen des KS-Tests, z.B. der Lilliefors-Test zum Testen auf Normalverteilung.
Variante: Test auf bestimmte Verteilung II
[Bearbeiten]Die Nullhypothese (: wahre Verteilungsfunktion von , : hypothetische Verteilungsfunktion) kann ersetzt werden durch
in R: mit ks.test und der Option alternative=" greater"
in R: mit ks.test und der Option alternative=" less"
Zweistichprobenfall
[Bearbeiten]Situation, Nullhypothese und benötigte Daten
[Bearbeiten]Situation: Gegeben seien zwei beliebige stetige ZV .
Nullhypothese: (Homogenitätstest)
benötigte Daten: unabhängige Stichproben und
Teststatistik
[Bearbeiten]Teststatistik: Man bestimmt zunächst (in Abhängigkeit von ) für und die relative Häufigkeit der Stichprobenwerte, die sind, also
(empirische Verteilungsfunktionen der beiden Stichproben)
Die Teststatistik berechnet sich als die maximale Abweichung zwischen beiden Werten, also
. Falls gilt, erwartet man nur eine geringe Abweichung. Damit spricht ein hoher Wert von gegen .
p-Wert und Durchführung in R
[Bearbeiten]-Wert: Die Verteilung von ist kompliziert. Man kann den -Wert mit Hilfe von Tabellen (für kleine ) oder Näherungsformeln (für große ) bestimmen. Wir wollen hier aber nicht näher auf die Berechnung eingehen.
Durchführung in R: mit dem Befehl ks.test: Einlesen der Stichproben in Vektoren und dann
Variante
[Bearbeiten]Die Nullhypothese ( bzw. : wahre Verteilungsfunktion von bzw. ) kann ersetzt werden durch
in R: mit ks.test und der Option alternative=" greater"
in R: mit ks.test und der Option alternative=" less"
Vorteile des KS-Tests
[Bearbeiten]- auch für kleine Stichproben geeignet.
- verteilungsfrei (es muss keine Verteilungsart vorausgesetzt werden).
- in R implementiert.
Nachteile des KS-Tests
[Bearbeiten]- recht aufwendig.
- anfällig gegenüber sogenannten "Bindungen". Treten in den Stichproben mehrfach dieselben Werte auf (z.B. künstlich erzeugt durch Runden), so liefert der KS-Test keine korrekten Resultate (-Werte) mehr.
- für diskrete verteilte Größen nur noch bedingt einsetzbar: Die Berechnung des -Werts wird möglicherweise ungenau, die Güte des Tests wird geringer und es treten häufig Probleme mit oben erwähnten Bindungen auf.
Der Shapiro-Wilks-Test
[Bearbeiten]Situation: Gegeben sei eine beliebige stetige ZV .
Nullhypothese: ist normalverteilt (Normalitätstest)
benötigte Daten: Stichprobe
Teststatistik und -Wert: kompliziert und aufwendig, wir wollen hier nicht näher darauf eingehen
Durchführung in R: Einlesen der Stichprobe in einen Vektor und dann
Beispiel
[Bearbeiten]Da der Shapiro-wilks-Test vergleichbar mit dem Anpassungstest ist, kann auf dieses Beispiel zurückgegriffen werden und wird hier nicht weiter aufgeführt.
Vorteile des SW-Tests
[Bearbeiten]- auch für kleine Stichproben gut geeignet (man erzielt insbesondere dann schon eine hohe Güte).
- verteilungsfrei (es muss keine Verteilungsart vorausgesetzt werden).
- in R implementiert.
Nachteile des SW-Tests
[Bearbeiten]- sehr speziell (nur für die Normalverteilungshypothese einsetzbar).
- anfällig gegenüber ’Ausreißern’ (bei einigen extrem großen oder extrem kleinen Werten in der Stichprobe kann die Nullhypothese fälschlicherweise abgelehnt werden).
- anfällig gegenüber Bindungen.
- recht aufwendig (insbesondere für große ) und schwer verständlich.
Der Bartlett-Test
[Bearbeiten]Situation und Nullhypothese
[Bearbeiten]Situation: Gegeben seien normalverteilte ZV .
Nullhypothese: (’Dispersionsvergleich’)
Anmerkung: Die Varianzgleichheit ist für weitere Tests (insbesondere den noch folgenden F-Test) eine benötigte Voraussetzung. Mit einem Bartlett-Test kann dies vorab empirisch überprüft werden.
Benötigte Daten
[Bearbeiten] unabhängige Stichproben
Dabei sollte für gelten (Faustregel).
Teststatistik I
[Bearbeiten]Man berechnet zunächst zu den einzelnen Stichproben:
- die arithmetischen Mittelwerte:
- die empirischen Varianzen
Daraus erhält man die sogenannte mittlere quadratische Abweichung der Fehler (’mean squared error’):
Teststatistik II
[Bearbeiten]Daraus berechnet sich mit die Teststatistik als
p-Wert
[Bearbeiten]
Dabei ist die -Verteilung mit Freiheitsgraden.
Durchführung in R
[Bearbeiten]Einlesen der Stichproben in einen gemeinsamen Vektor x zusammen mit einem Faktor g (gleicher Länge), der angibt zu welcher Größe die jeweiligen Komponenten von x gehören. Dann: bartlett.test(x ~ g)
Alternativ: Einlesen der einzelnen Stichproben in Vektoren, etwa x1,x2,,xm und dann: bartlett.test(list(x1,x2,,xm))
Anmerkung
[Bearbeiten]Der Bartlett-Test ist anfällig gegenüberber Verletzungen der Normalverteilungsannahme. Sind die Größen nicht normalverteilt, so liefert der Test keine korrekten Resultate (-Werte).
Beispiel 1.1
[Bearbeiten]Verschiedene Drahtsorten () werden auf Zugfestigkeit untersucht.
Wir nehmen an, dass die ZV , die die Zugfestigkeiten der verschiedenen Sorten beschreiben, normalverteilt mit den Standardabweichungen sind und untersuchen zunächst die Nullhypothese
Beispiel 1.2
[Bearbeiten]Man erhält folgende Daten (in ):
Damit berechnet sich der -Wert als , es liegt also kein signifikantes Ergebnis vor.
Der Kruskal-Wallis-Rangsummentest
[Bearbeiten]Situation, Nullhypothese und benötigte Daten
[Bearbeiten]Situation: Gegeben seien beliebige ZV .
Nullhypothese: sind identisch verteilt (’Homogenitätstest’)
benötigte Daten: unabhängige Stichproben zu
Teststatistik und p-Wert
[Bearbeiten]Dies wollen wir an dieser Stelle nicht ausführen.
Man beachte aber, dass zur Durchführung des Tests nur die ’Ränge’ der Stichprobenwerte verwendet werden. Die Differenzen zwischen den Werten beeinflussen das Testergebnis nicht. Daher ist der Kruskal-Wallis-Test auch für ZV geeignet, deren Ausprägungen nur ordinalskaliert sind.
Durchführung in R
[Bearbeiten]Einlesen der Stichproben in einen gemeinsamen Vektor x zusammen mit einem Faktor g (gleicher Länge), der angibt zu welcher Größe die jeweiligen Komponenten von x gehören. Dann: kruskal.test(x,g)
Alternativ: Einlesen der einzelnen Stichproben in Vektoren, etwa x1,x2,,xm und dann: kruskal.test(list(x1,x2,...,xm))
Dixon’s Q-Test
[Bearbeiten]Mit dem Dixon’s -Test können Ausreißer identifiziert werden. Dieser Test soll unter anderem laut Dixon sparsam und maximal einmal pro Datensatz verwendet werden und kann für beide Seiten gleichermaßen verwendet werden.
Situation, Nullhypothese und Teststatistik
[Bearbeiten]Situation: Gegeben sei eine normalverteilte ZV .
Nullhypothese:
Benötigte Daten: Geordnete Datenreihe mit Elementen.
Teststatistik : Für die Teststatistik wird die absolute Differenz zwischen dem zu untersuchenden Wert und dem nächsten Wert (da geordnete Datenreihe oder ) bestimmt und anschließend durch die Spannweite geteilt.
Verwerfen der Hypothese
[Bearbeiten]Gilt , so kann abgelehnt werden (d.h. ist kein Ausreißer). erhält man abhängig von der Stichprobengröße und dem Konvidenzniveau aus der entsprechenden Tabelle.
Beispiel
[Bearbeiten]Stichprobe mit Werten und Konvidenznveau :
ist ein Ausreißer.
kann abgelehnt werden - ist somit kein Ausreißer.
Seiteninformation
[Bearbeiten]Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Kurzvorstellung%20weiterer%20Hypothesentests
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.
















![{\displaystyle T^{\ast }=\max \limits _{b\in \mathbb {R} }\left|{\hat {F}}(b)-F(b)\right|\quad \left({\text{also:}}\ T\in ]0,1[\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e8970dddeefbf52831f90efab33888fe1a7ba30)










![{\textstyle [a_{0},b_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f839ad89da1402f5675ec53a3cb6105c2de966b)