Kurs:Statistik für Anwender/Normalverteilte Zufallsvariablen
Normalverteilte Zufallsvariable
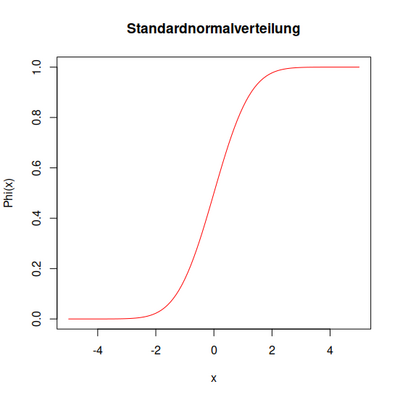
[Bearbeiten]Standardnormalverteilung
[Bearbeiten]Gaußsche Dichtefunktion
[Bearbeiten]Die Funktion
heißt Gaußche Dichtefunktion (bzw. Gaußsche Glockenkurve). Es gilt .
Verteilungsfunktion
[Bearbeiten]Folglich ist die Dichtefunktion einer ZV mit Verteilungsfunktion
Man nennt die Standardnormalverteilung. Zufallsvariablen mit Dichte , nennt man standardnormalverteilt.
Berechnung in R
[Bearbeiten]Da das Integral über nicht geschlossen lösbar ist, benutzt man geeignete Software zur Berechnung von .
In R erhält man durch pnorm().
Eigenschaften der Standardnormalverteilung
[Bearbeiten]Einige wichtige Eigenschaften von und :
Eigenschaften der Standardnormalverteilung I
[Bearbeiten]- Die Dichtefunktion ist symmetrisch zur -Achse. Sie ist monoton wachsend auf und monoton fallend auf , hat also die Maximumstelle . Wendepunkte liegen an den Stellen . Es gilt .
Eigenschaften der Standardnormalverteilung II
[Bearbeiten]- Für alle gilt . Folglich gilt für eine standardnormalverteilte ZV stets:
Eigenschaften der Standardnormalverteilung III
[Bearbeiten]- Eine standardnormalverteilte ZV hat Erwartungswert und Varianz .
Beispiel Standardnormalverteilte ZV
[Bearbeiten]Für eine standardnormalverteilte ZV gilt:
Außerdem ist
und analog
Normalverteilung
[Bearbeiten]Dichtefunktion
[Bearbeiten]Seien und gegeben.
Eine ZV mit der W-Dichte
heißt normalverteilt mit EW und SA .
Verteilungsfunktion
[Bearbeiten]Für die Verteilungsfunktion von gilt dann:
Dabei ist definiert durch:
Beachte: kann nur (computerunterstützt) näherungsweise berechnet werden, da obiges Integral nicht analytisch gelöst werden kann.
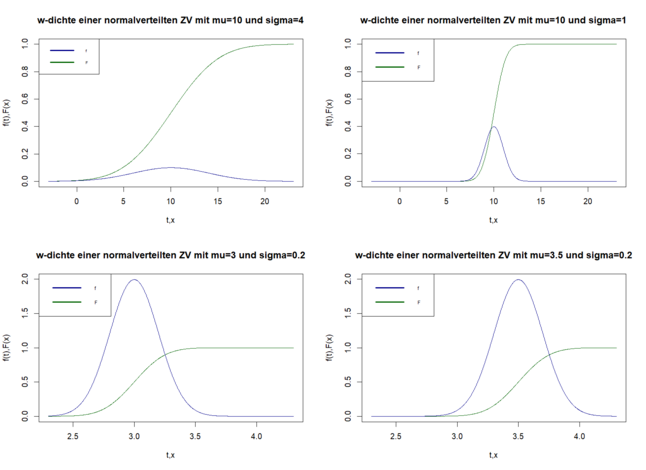
Beispiel Dichte- und Verteilungsfunktion
[Bearbeiten]Beispiel Dichte- und Verteilungsfunktion interkativ
[Bearbeiten]Interaktive Shiny-App zur Normalverteilung:
Download und Link
Anmerkungen zur Normalverteilung I
[Bearbeiten]Der EW entspricht der Maximumstelle von . Daher ist es wahrscheinlicher, dass eine Realisation einer normalverteilten ZV in der Nähe des EW liegt, als dass sie (in einem gleich großen Bereich) weit vom EW entfernt liegt.
ist symmetrisch bezüglich der Parallellen zur -Achse durch . Die Wahrscheinlichkeit, dass eine Realisation von in einem bestimmten Bereich liegt ist genauso groß wie die Wahrscheinlichkeit, dass sie in dem am EW gespiegelten Bereich liegt.
Anmerkungen zur Normalverteilung II
[Bearbeiten]Ist groß, so ist die Kurve breiter, d.h. die Wahrscheinlichkeit dafür, dass eine Realisation von weit entfernt vom EW liegt, ist dann größer. Ist klein, so liegen die Realisationen von mit noch höherer Wahrscheinlichkeit in der Nähe des EW.
Berechnung von Wahrscheinlichkeiten
[Bearbeiten]Für eine normalverteilte ZV mit EW und Standardabweichung gilt für beliebige Zahlen mit :
Beispiel Berechnung von Wahrscheinlichkeiten
[Bearbeiten]Für eine normalverteilte Größe mit und gilt:
Für eine normalverteilte Größe mit und gilt:
Erwartungswert und Standardabweichung
[Bearbeiten]Für eine normalverteilte ZV mit EW und Standardabweichung gilt:
Praktische Anwendung der NV
[Bearbeiten]Viele in Natur und Umwelt vorkommenden ZV sind (zumindest näherungsweise) normalverteilt. In der Tat kann dies mathematisch erklärt werden. Nach dem Zentralen Grenzwertsatz ist jede ZV, die sich als Summe vieler unabhängiger ZV ergibt (unter gewissen, meist erfüllten Bedingungen) annähernd normalverteilt.
Beispiele Anwendung der NV I
[Bearbeiten]- Eine binomialverteilte Größe ( Versuche, Trefferwahrscheinlicheit ) ist annnähernd normalverteilt mit und , wenn groß ist (auf diesen Fall gehen wir später nochmals ausführlicher ein).
- Die ZV für die Summe der Augenzahlen beim Werfen vieler Würfel ist annähernd normalverteilt.
- Zeitspannen, die sich aus vielen (unabhängigen) kleinen Einheiten zusammensetzen, können als näherungsweise normalverteilt angenommen werden, beispielsweise die Zeit, die ein Kundenberater für 20 telefonische Beratungsgespräche braucht.
Beispiele Anwendung der NV II
[Bearbeiten]- Zufällig zustandegekommene Messfehler sind oft näherungsweise normalverteilt mit Erwartungswert (im Gegensatz zu systematischen Messfehlern).
- Der Ertrag einer Ernte ist abhängig von vielen zufälligen Einflüssen. Nimmt man an, dass diese Faktoren unabhängig voneinander gewisse Beiträge liefern, so folgt daraus, dass der Ernteertrag näherungsweise normalverteilt ist.
Berechnung in R
[Bearbeiten]Für eine normalverteilte ZV mit EW und Standardabweichung berechnet man in R:
- die Funktionswerte der W-Dichte von durch:
- die Funktionswerte der VF von durch:
- die Wahrscheinlichkeit für durch:
Aufgabe 1.1
[Bearbeiten]Setzen Sie alle Parameter in die bekannten Formeln zur Berechnung der Wahrscheinlichkeiten bei normalverteilten ZVen ein und nutzen Sie dann zur Berechnung den R-Befehl pnorm.
1. Berechnen Sie für eine mit EW und Standardabweichung normalverteilte ZV die Wahrscheinlichkeiten:
2. Plotten Sie mit R den Graph der Dichtefunktion von X aus Aufgabe a). Markieren Sie die in Aufgabe a) berechneten Wahrscheinlichkeiten in einem Ausdruck des geplotteten Graphen.
Aufgabe 1.2
[Bearbeiten]3. Zeigen Sie, dass bei einer normalverteilten Zufallsvariable mit EW und Standardabweichung die Wahrscheinlichkeiten
nicht von und abhängen und berechnen Sie diese Wahrscheinlichkeitswerte.
4. Sortieren Sie (ohne zu rechnen) für eine normalverteilte Zufallsvariable mit und die folgenden Wahrscheinlichkeiten der Größe nach: , , , , .
Aufgabe 1.3
[Bearbeiten]5. Sortieren Sie (ohne zu rechnen) für eine normalverteilte Zufallsvariablen die Wahrscheinlichkeitswerte für für die folgenden Werte von und der Größe nach:
und ,
und ,
und ,
und .
Sigma-Regeln
[Bearbeiten](-Regeln für normalverteilte ZV)
Wir betrachten eine normalverteilte ZV mit EW und Standardabweichung . Dann gilt:
Beispiel Sigma-Regeln
[Bearbeiten]Speziell für ergeben sich die -Regeln:
d.h. ca. 68,27% der Werte von liegen näher als beim EW
d.h. ca. 95,45% der Werte von liegen näher als beim EW
d.h. ca. 99,73% der Werte von liegen näher als beim EW
Der Zentrale Grenzwertsatz
[Bearbeiten]In der Praxis treten oft ZV auf, die (annähernd) normalverteilt sind. Dies lässt sich mit mathematischen Methoden erklären. Grundlage dafür ist der folgende sogenannte Zentrale Grenwertsatz, der (etwas präziser formuliert) bewiesen werden kann:
ZV als Summe vieler unabhängiger ZV
[Bearbeiten]Falls eine ZV mit Erwartungswert und Standardabweichung die Summe von vielen unabhängigen ZV ist (also: mit groß), so gilt (unter gewissen Zusatzvoraussetzungen, die wir hier nicht diskutieren wollen, die aber in der Praxis oft erfüllt sind):
entspricht in diesem Sinne also näherungsweise einer Normalverteilung mit demselben Ewartungswert und derselben Standardabweichung.
Spezialfall
[Bearbeiten]Ein wichtiger Spezialfall davon ist die folgende Situation: Von einer ZV ist nur der Erwartungswert und die Standardabweichung bekannt. Ansonsten weiß man nichts über die Art der Verteilung. Nun sei die Summe von unabhängigen ZV, die alle diesselbe Verteilung wie haben. Dann ist approximativ normalverteilt mit .
Beispiel 1.1
[Bearbeiten] Würfel werden geworfen. Die ZV beschreibt die Augensumme. Damit folgt, dass ist, wobei unabhängig sind und alle dieselbe Wahrscheinlichkeitsverteilung haben wie die ZV für die Zahl eines einzelnen Würfels ( beschreibt die Zahl des -ten Würfels). Es gilt:
Nach dem Zentralen Grenzwertsatz ist approximativ normalverteilt mit und . Also folgt etwa:
Beispiel 1.2
[Bearbeiten]Da nur ganzzahlige Werte annehmen kann, kann die durch jede Zahl aus dem halboffenen Intervall ersetzt werden. Mit dem mittleren Wert hofft man auf eine möglichst gute Approximation.
Auf der rechten Seite kann jede Zahl aus dem halboffenen Intervall stehen. Erneut wählt man den mittleren Wert mit dem Ziel einer möglichst guten Approximation.
Beispiel 2
[Bearbeiten] sei die ZV für die Dauer (in Minuten) eines Gespräch eines Telefonberaters (bekannt sei hier, dass und ).
ist dann die ZV für die Dauer von (unabhängigen) Gesprächen.
Dann ist
Man kann also als approximativ normalverteilt mit und annehmen.
Beispiel 3
[Bearbeiten]Die Lebensdauer eines elektronischen Bauteils (in Tagen) ist exponentialverteilt zum Parameter . Dann gilt und .
Man hat nun 50 der Bauteile zur Vefügung und setzt diese nacheinander ein (solange sie funktionieren). Die ZV , die die Gesamtlaufzeit beschreibt ist dann die Summe der 50 einzelnen Laufzeiten, also , wobei unabhängig voneinander sind und alle die gleiche Verteilung haben (dieselbe wie ). Folglich ist approximativ normalverteilt mit . Also folgt beispielsweise:
Praktische Anwendung des ZGWS
[Bearbeiten]In der Praxis kann man oft davon ausgehen (bzw. vermuten), dass eine ZV die Summe von unabhängigen ZV ( groß) ist. Dann folgt aus dem Zentralen Grenzwertsatz, dass approximativ normalverteilt ist.
Beispiel 1
[Bearbeiten]Sei die ZV für die Zeit, die ein bestimmter Student morgens vom Aufstehen bis zum Erreichen der Uni benötigt. Dann gilt etwa:
Wenn man davon ausgeht, dass diese ZV alle unahängig sind, dann liegt die Vermutung nahe, dass normalverteilt ist ( und sind dann allerdings zunächst unbekannt).
Beispiel 2
[Bearbeiten]Die Regenmenge in einem Jahr (an einem bestimmten Ort) ist die Summe der Regenmengen an den 365 Tagen dieses Jahres. Diese Tagesregenmengen sind weitgehend (aber nicht vollständig) unabhängig voneinander, denn es gibt kaum einen Zusammenhang zwischen den Regenmengen zweier Tage, die nicht zu nah beisammen liegen. Die Regenmenge eines einzelnen Tages ist sicherlich nicht normalverteilt, die jährliche Regenmenge hingegen (approximativ) schon.
Aufgabe 3
[Bearbeiten]Die Zufallsvariable beschreibe die Zeit (in Minuten), die man insgesamt warten muss, wenn man -mal (unabhängig voneinander) mit der Bahn fährt. Dabei sei jede einzelne Wartezeit als gleichverteilt auf dem Intervall angenommen.
(Das ist sinnvoll, wenn die Bahn alle Minuten fährt und man zu einem zufälligen Zeitpunkt zur Haltestelle kommt).
Nach dem zentralen Grenzwertsatz (ZGWS) ist (näherungsweise) normalverteilt.
Berechnen Sie zunächst die Parameter und der (näherungsweise) normalverteilten ZV und damit dann die Wahrscheinlichkeit, dass Sie eine Gesamtwartezeit zwischen 1000 und 1100 Minuten haben.
Aufgabe 4
[Bearbeiten]Die Lebensdauer (in Betriebsstunden) eines elektronischen Bauteils sei exponentialverteilt mit Parameter . Eine Firma hat dieser Bauteile zur Verfügung, die nacheinander eingesetzt werden können (es wird immer nur eines benötigt). Berechnen Sie die Wahrscheinlichkeit, dass die Bauteile insgesamt mindestens Betriebsstunden funktionieren.
Es sei hierzu die Betriebsdauer eines Bauteils und für alle . Außerdem sei die Betriebszeit der einzelnen Bauteile als unabhängig voneinander angenommen. Dann ist die Gesamtbetirebsdauer aller Bauteile näherungsweise normalverteilt. Berechnen Sie und .
Approximation der Binomialverteilung mit der Normalverteilung
[Bearbeiten]Binomialverteilung
[Bearbeiten]Einen Spezialfall des Zentralen Grenzwertsatzes erhält man bei der Betrachtung einer binomialverteilten ZV . Es ist:
Binomialverteilung bei großer Stichprobe 1
[Bearbeiten]Falls groß ist, kann man daher die Wahrscheinlichkeit näherungsweise berechnen, indem man durch eine normalverteilte ZV mit Erwartungswert und Standardabweichung ersetzt, es gilt also:
Binomialverteilung bei großer Stichprobe 2
[Bearbeiten]Ist speziell , so gilt (weil nur ganze Zahlen annehmen kann)
und folglich
Beispiel
[Bearbeiten]- Für und gilt:
- Für und gilt:
Punktschätzungen für den Erwartungswert und Standardabweichung
[Bearbeiten]Sei eine normalverteilte ZV, für die und unbekannt sind.
Basierend auf einer Stichprobe sind folgende Punktschätzungen sinnvoll:
- wird geschätzt durch:
- wird geschätzt durch:
Intervallschätzung für Erwartungswert und Standardabweichung
[Bearbeiten]Bestimmung Standardabweichung und arithmetisches Mittel
[Bearbeiten]Sei eine normalverteilte ZV, für die und unbekannt sind.
Basierend auf einer Stichprobe berechnet man zunächst
Davon ausgehend kann man nun wie folgt Intervallschätzungen für bzw. zu einem vorgegebenen Konfidenzniveau berechnen:
Intervallschätzungen für Erwartungswert
[Bearbeiten]Ist die Zahl mit , so erhält man eine Intervallschätzung für durch:
Intervallschätzungen für Erwartungswert in R
[Bearbeiten]Diese Konfidenzintervalle für können in R direkt berechnet werden. Sind die Daten der Stichprobe in einem Vektor eingetragen, so ergibt der Befehl ein Konfidenzintervall zum Konfidenzniveau .
Intervallschätzungen für Standardabweichung in R
[Bearbeiten]
Sind und die Zahlen mit
so erhält man eine Intervallschätzung für durch:
Einhaltung des Konfidenzniveaus
[Bearbeiten]Es ist bewiesen, dass diese Methoden zur Berechnung von Intervallschätzungen für bzw. beide das vorgegebene Konfidenzniveau einhalten, das heißt unabhängig von den wahren Werten von und ist vor der Erhebung der Daten garantiert:
Anmerkungen
[Bearbeiten]- Hier gilt sogar:
- Man beachte, dass dabei die Intervallgrenzen und bzw. und vom Zufall abhängen (denn für ihre Berechnung werden die Daten verwendet). Andererseits sind und zwar unbekannt, aber fest und hängen daher nicht vom Zufall ab. Nachdem man die Konfidenzintervalle berechnet hat, sind die Aussagen bzw. daher entweder wahr oder falsch, man kann ihnen aber keine Wahrscheinlichkeit mehr zuweisen.
Beispiel:
[Bearbeiten]Wir betrachten die ZV , die die jährliche Regenmenge an einem bestimmten Ort (in mm) beschreibt. Wir gehen dabei davon aus, dass normalverteilt ist (dies ist plausibel, denn ist die Summe von täglichen Regenmengen, die in weiten Teilen annähernd unabhängig voneinander sind).
Es liegt eine Stichprobe über Jahre mit den folgenden Daten vor:
Wir berechnen nun Intervallschätzungen für und zum Konfidenzniveau :
- IVS für :
- IVS für :
Man bestimmt zunächst die Zahlen mit:
Aufgabe 1.1
[Bearbeiten]Ein Düngemittel soll auf Wirksamkeit untersucht werden. Eine Messreihe ergibt für das Wachstum einer behandelten Pflanze innerhalb einer Woche die folgende (für ein sinnvolles Experiment deutlich zu kurze) Urliste von Werten (in cm): Wir nehmen an, dass das Merkmal Wachstum durch eine normalverteilte Zufallsvariable mit unbekannten Parametern und beschrieben werden kann.
- Geben Sie eine Punktschätzung für die Paramter und der normalverteilten ZV an.
Aufgabe 1.2
[Bearbeiten]Wir nehmen nun an, dass diese Schätzungen den wahren Werten von und entsprechen. Wie groß ist dann die Wahrscheinlichkeit, dass eine behandelte Pflanze innerhalb einer Woche
- zwischen 8 cm und 12 cm wächst?
- exakt 9.73 cm gewachsen ist?
- mit 10.8 cm Wachstum gemessen wird, wenn die Messmethode bis auf einen Millimeter genau ist?
Berechnen Sie Intervallschätzungen für und zum Konfidenzniveau .
Aufgabe 2
[Bearbeiten]Ein Umweltwissenschaftler untersucht den Einfluss verschiedener Habitate auf das Gewicht der Waldspitzmaus (Sorex araneus). Dazu wird das Gewicht der untersuchten Mäuse als normalverteilt mit unbekannten Parametern und angenommen. Bei einer Untersuchung werden Mäuse gewogen. Man ermittelt aus den Daten (angegeben in Gramm) den arithmetischen Mittelwert und die empirische Standardabweichung .
Berechnen Sie Punkt- und Intervallschätzungen für und zum Konfidenzniveau .
Aufgabe 3.1
[Bearbeiten]Wie verändert sich die Breite eines Konfidenzintervalls für den unbekannten Erwartungswert einer normalverteilten Zufallsvariable , basierend auf einer Stichprobe der Länge n, zum Konfidenzniveau , falls
- größer wird und , , unverändert bleiben ?
- größer wird und und unverändert bleiben ?
- größer wird und und unverändert bleiben ?
- größer wird und und unverändert bleiben ?
Aufgabe 3.2
[Bearbeiten]Wie verändert sich die Breite eines Konfidenzintervalls für die unbekannte Standardabweichung einer normalverteilten Zufallsvariable , basierend auf einer Stichprobe der Länge n, zum Konfidenzniveau , falls
- größer wird und und unverändert bleiben ?
- größer wird und und unverändert bleiben ?
- größer wird und und unverändert bleiben ?
Seiteninformation
[Bearbeiten]Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.
Wiki2Reveal
[Bearbeiten]Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.
- Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
- Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Normalverteilte%20Zufallsvariablen
- siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.









![{\textstyle ]-\infty ,0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/668b54e9f75e989d19a237a8d9f2f8a1010a563d)













































![{\displaystyle X\in [u,v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7bfef2636d734cecbe28f4ca7f0ea26b00ba9f6)





















![{\textstyle P\left(X\in [\mu -\sigma ,\mu +\sigma ]\right)\approx 0.6827}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864a400976d585e942062d1c08d42c4af55830f8)
![{\textstyle P\left(X\in [\mu -2\sigma ,\mu +2\sigma ]\right)\approx 0.9545}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f114f479c65833376a711ca89d33a80b6dd73277)

![{\textstyle P\left(X\in [\mu -3\sigma ,\mu +3\sigma ]\right)\approx 0.9973}](https://wikimedia.org/api/rest_v1/media/math/render/svg/853849e2acb1ec6ca75f2deeb4043c84204e4f2d)














































![{\textstyle \left[0,7\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ae964ba767893597244ea628b2a0bfbe04123b)



































![{\textstyle q\left(=q_{\left[t,n-1,{\frac {1+\delta }{2}}\right]}\right)\in \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b143eabcc1324d12efc5b280e7beff4181bbf00d)

![{\textstyle [\mu _{U},\mu _{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3326d8d70557cff6b7c142555d3137bf994c12a1)
![{\displaystyle [\mu _{U},\mu _{O}]=\left[\ {\overline {x}}-c\ ,\ {\overline {x}}+c\ \right]\quad {\text{mit}}\quad c=q\cdot {\frac {s_{X}}{\sqrt {n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3fb44a9ecc5c07cee766e180d014325dfe6bb1b4)
![{\textstyle \color {blue}{t.test(x,}\color {blue}{conf.level}\color {blue}{=\delta )\$}\color {blue}{conf.int[1:2]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21804ec7c5aedf36948e8caa6414488ab1b3a9d7)

![{\textstyle q_{U}=\left(=q_{\left[\chi ^{2},n-1,{\frac {1+\delta }{2}}\right]}\right)\in ]0,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/04a1ab170b5b6efd298cf360000204a0733ded6a)
![{\textstyle q_{O}=\left(=q_{\left[\chi ^{2},n-1,{\frac {1-\delta }{2}}\right]}\right)\in ]0,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/447c49c93ecd906eb08d0662cec3c410b29bb9e8)

![{\textstyle [\sigma _{U},\sigma _{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1667ccc663b1d537c9bfa747cbea0d6cd8625d24)
![{\displaystyle [\sigma _{U},\sigma _{O}]=\left[\ {\sqrt {\frac {(n-1){s_{X}}^{2}}{q_{U}}}}\ ,\ {\sqrt {\frac {(n-1){s_{X}}^{2}}{q_{O}}}}\ \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/394720ef2a22c9a2a436a6d74fd25f5f64d3fbd9)
![{\displaystyle P\left(\mu \in [\mu _{U},\mu _{O}]\right)\geq \delta \quad {\text{und}}\quad P\left(\sigma \in [\sigma _{U},\sigma _{O}]\right)\geq \delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f8e061351918c684e9098f5ef46e5f09b95b6bd)
![{\textstyle \quad P\left(\mu \in [\mu _{U},\mu _{O}]\right)=\delta \ {\text{und}}\ P\left(\sigma \in [\sigma _{U},\sigma _{O}]\right)=\delta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2228e1541f46c1fa19350afcc4feb2b6254481e7)




![{\textstyle \mu \in [\mu _{U},\mu _{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e401dd3c95181d51374fb8a4a0a9163fcd49c1d)
![{\textstyle \sigma \in [\sigma _{U},\sigma _{O}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43b8b135d850bebc9864e329e7e789f115261e50)




![{\textstyle [\mu _{U},\mu _{O}]=[732.44,790.36]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8099afba204e2188d23b60789f3fd18736592de3)
![{\textstyle q_{U},q_{O}\in ]0,\infty [}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a415c4baa32a9c6a26b41e2e46b9f015a4a18ba1)
![{\textstyle [\sigma _{U},\sigma _{O}]=\left[84.756,127.014\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35536d44e83905ea98e7311ff917e3b289407c8d)









