Kurs:Statistik für Anwender/Verknüpfung diskreter Zufallsvariablen

Verknüpfung diskreter ZV

Sei ${\textstyle (\Omega ,P)}$ ein W-Raum, ${\textstyle X,Y:\Omega \to \mathbb {R} }$ ZV auf ${\textstyle \Omega }$ und ${\textstyle a,b\in \mathbb {R} ,\ n\in \mathbb {N} }$. Dann erhält man weitere ZV auf ${\textstyle \Omega }$ durch
$$a\cdot X+b:\Omega \to \mathbb {R} ,\ \omega \mapsto a\cdot X(\omega )+b,$$ $$X^{n}:\Omega \to \mathbb {R} ,\ \omega \mapsto X(\omega )^{n}$$ $$X+Y:\Omega \to \mathbb {R} ,\ \omega \mapsto X(\omega )+Y(\omega ),$$ $$X\cdot Y:\Omega \to \mathbb {R} ,\ \omega \mapsto X(\omega )\cdot Y(\omega ),$$ $$X-Y:\Omega \to \mathbb {R} ,\ \omega \mapsto X(\omega )-Y(\omega ),$$ $${\text{(weitere Verknüpfungen von ZV sind denkbar)}}$$

Gemeinsame Verteilung zweier endlicher ZV und Unabhängigkeit

(Gemeinsame W-Funktion zweier endlicher ZV)
Gegeben seien zwei endliche ZV ${\textstyle X,Y,}$ wobei ${\textstyle X}$die Werte ${\textstyle a_{1},\ldots ,a_{m}}$ und ${\textstyle Y}$die Werte ${\textstyle b_{1},\ldots ,b_{\ell }}$ annehmen kann.

Gemeinsame Wahrscheinlichkeitsfunktion

Die Funktion
$$\{a_{1},\ldots ,a_{m}\}\times \{b_{1},\ldots ,b_{\ell }\}\to [0,1]\ ,\ (a_{j},b_{k})\mapsto P(X=a_{j}\wedge Y=b_{k})$$
heißt gemeinsame Wahrscheinlichkeitsfunktion von ${\textstyle X}$ und ${\textstyle Y.}$ Man kann sie übersichtlich in Form einer Tabelle darstellen, wobei die möglichen Werte ${\textstyle a_{1},\ldots ,a_{m}}$ für ${\textstyle X}$ zu den einzelnen Spalten und die möglichen Werte ${\textstyle b_{1},\ldots ,b_{\ell }}$ für ${\textstyle Y}$ zu den einzelnen Zeilen gehören. In die Spalte zu ${\textstyle a_{j}}$ und die Zeile zu ${\textstyle b_{k}}$ trägt man dann die Wahrscheinlichkeit ${\textstyle P(X=a_{j}\wedge Y=b_{k})}$ ein.

Beispiel 1

Zwei Laplace-Würfel werden geworfen. Die ZV ${\textstyle X}$ gibt die Zahl auf dem ersten und die ZV ${\textstyle Y}$ gibt die Zahl auf dem zweiten Würfel an. Die gemeinsame W-Funktion sieht wie folgt aus: $${\begin{array}{|c||c|c|c|c|c|c||c|}\hline &b_{1}=1&b_{2}=2&b_{3}=3&b_{4}=4&b_{5}=5&b_{6}=6&{\text{Summe}}\\\hline \hline &P(X=1\wedge Y=1)&P(X=1\wedge Y=2)&P(X=1\wedge Y=3)&P(X=1\wedge Y=4)&P(X=1\wedge Y=5)&P(X=1\wedge Y=6)&P(X=1)\\a_{1}=1&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{6}}\\\hline &P(X=2\wedge Y=1)&P(X=2\wedge Y=2)&P(X=2\wedge Y=3)&P(X=2\wedge Y=4)&P(X=2\wedge Y=5)&P(X=2\wedge Y=6)&P(X=2)\\a_{2}=2&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{6}}\\\hline &P(X=3\wedge Y=1)&P(X=3\wedge Y=2)&P(X=3\wedge Y=3)&P(X=3\wedge Y=4)&P(X=3\wedge Y=5)&P(X=3\wedge Y=6)&P(X=3)\\a_{3}=3&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{6}}\\\hline &P(X=4\wedge Y=1)&P(X=4\wedge Y=2)&P(X=4\wedge Y=3)&P(X=4\wedge Y=4)&P(X=4\wedge Y=5)&P(X=4\wedge Y=6)&P(X=4)\\a_{4}=4&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{6}}\\\hline &P(X=5\wedge Y=1)&P(X=5\wedge Y=2)&P(X=5\wedge Y=3)&P(X=5\wedge Y=4)&P(X=5\wedge Y=5)&P(X=5\wedge Y=6)&P(X=5)\\a_{5}=5&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{6}}\\\hline &P(X=6\wedge Y=1)&P(X=6\wedge Y=2)&P(X=6\wedge Y=3)&P(X=6\wedge Y=4)&P(X=6\wedge Y=5)&P(X=6\wedge Y=6)&P(X=6)\\a_{6}=6&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{36}}&{\frac {1}{6}}\\\hline \hline &P(Y=1)&P(Y=2)&P(Y=3)&P(Y=4)&P(Y=5)&P(Y=6)&\\{\text{Summe}}&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\\&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&1\\\hline \end{array}}$$

Beispiel 2.1

Ein Laplace-Würfel, bei dem sich die Augenzahlen ${\textstyle 1}$ und ${\textstyle 6}$, sowie ${\textstyle 2}$ und ${\textstyle 5}$ sowie ${\textstyle 3}$ und ${\textstyle 4}$ gegenüberliegen, wird geworfen. Die ZV ${\textstyle X}$ gibt die Zahl auf der Oberseite und die ZV ${\textstyle Y}$ gibt die Zahl auf der Unterseite des Würfels an.

Beispiel 2.2

Die gemeinsame W-Funktion sieht wie folgt aus: $${\begin{array}{|c||c|c|c|c|c|c||c|}\hline &b_{1}=1&b_{2}=2&b_{3}=3&b_{4}=4&b_{5}=5&b_{6}=6&{\text{Summe}}\\\hline \hline &P(X=1\wedge Y=1)&P(X=1\wedge Y=2)&P(X=1\wedge Y=3)&P(X=1\wedge Y=4)&P(X=1\wedge Y=5)&P(X=1\wedge Y=6)&P(X=1)\\a_{1}=1&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&0&0&0&0&0&{\frac {1}{6}}&{\frac {1}{6}}\\\hline &P(X=2\wedge Y=1)&P(X=2\wedge Y=2)&P(X=2\wedge Y=3)&P(X=2\wedge Y=4)&P(X=2\wedge Y=5)&P(X=2\wedge Y=6)&P(X=2)\\a_{2}=2&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&0&0&0&0&{\frac {1}{6}}&0&{\frac {1}{6}}\\\hline &P(X=3\wedge Y=1)&P(X=3\wedge Y=2)&P(X=3\wedge Y=3)&P(X=3\wedge Y=4)&P(X=3\wedge Y=5)&P(X=3\wedge Y=6)&P(X=3)\\a_{3}=3&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&0&0&0&{\frac {1}{6}}&0&0&{\frac {1}{6}}\\\hline &P(X=4\wedge Y=1)&P(X=4\wedge Y=2)&P(X=4\wedge Y=3)&P(X=4\wedge Y=4)&P(X=4\wedge Y=5)&P(X=4\wedge Y=6)&P(X=4)\\a_{4}=4&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&0&0&{\frac {1}{6}}&0&0&0&{\frac {1}{6}}\\\hline &P(X=5\wedge Y=1)&P(X=5\wedge Y=2)&P(X=5\wedge Y=3)&P(X=5\wedge Y=4)&P(X=5\wedge Y=5)&P(X=5\wedge Y=6)&P(X=5)\\a_{5}=5&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&0&{\frac {1}{6}}&0&0&0&0&{\frac {1}{6}}\\\hline &P(X=6\wedge Y=1)&P(X=6\wedge Y=2)&P(X=6\wedge Y=3)&P(X=6\wedge Y=4)&P(X=6\wedge Y=5)&P(X=6\wedge Y=6)&P(X=6)\\a_{6}=6&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{6}}&0&0&0&0&0&{\frac {1}{6}}\\\hline \hline &P(Y=1)&P(Y=2)&P(Y=3)&P(Y=4)&P(Y=5)&P(Y=6)&\\{\text{Summe}}&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\\&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&1\\\hline \end{array}}$$

Beispiel 3.1

Ein Laplace-Würfel, bei dem sich die Augenzahlen ${\textstyle 1}$ und ${\textstyle 6}$, sowie ${\textstyle 2}$ und ${\textstyle 5}$ sowie ${\textstyle 3}$ und ${\textstyle 4}$ gegenüberliegen, wird geworfen. Die ZV ${\textstyle X}$ gibt die Zahl auf der Oberseite und die ZV ${\textstyle Y}$ gibt die Zahl auf der Vorderseite des Würfels an.

Beispiel 3.2

Die gemeinsame W-Funktion sieht wie folgt aus: $${\begin{array}{|c||c|c|c|c|c|c||c|}\hline &b_{1}=1&b_{2}=2&b_{3}=3&b_{4}=4&b_{5}=5&b_{6}=6&{\text{Summe}}\\\hline \hline &P(X=1\wedge Y=1)&P(X=1\wedge Y=2)&P(X=1\wedge Y=3)&P(X=1\wedge Y=4)&P(X=1\wedge Y=5)&P(X=1\wedge Y=6)&P(X=1)\\a_{1}=1&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&0&{\frac {1}{24}}&{\frac {1}{24}}&{\frac {1}{24}}&{\frac {1}{24}}&0&{\frac {1}{6}}\\\hline &P(X=2\wedge Y=1)&P(X=2\wedge Y=2)&P(X=2\wedge Y=3)&P(X=2\wedge Y=4)&P(X=2\wedge Y=5)&P(X=2\wedge Y=6)&P(X=2)\\a_{2}=2&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{24}}&0&{\frac {1}{24}}&{\frac {1}{24}}&0&{\frac {1}{24}}&{\frac {1}{6}}\\\hline &P(X=3\wedge Y=1)&P(X=3\wedge Y=2)&P(X=3\wedge Y=3)&P(X=3\wedge Y=4)&P(X=3\wedge Y=5)&P(X=3\wedge Y=6)&P(X=3)\\a_{3}=3&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{24}}&{\frac {1}{24}}&0&0&{\frac {1}{24}}&{\frac {1}{24}}&{\frac {1}{6}}\\\hline &P(X=4\wedge Y=1)&P(X=4\wedge Y=2)&P(X=4\wedge Y=3)&P(X=4\wedge Y=4)&P(X=4\wedge Y=5)&P(X=4\wedge Y=6)&P(X=4)\\a_{4}=4&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{24}}&{\frac {1}{24}}&0&0&{\frac {1}{24}}&{\frac {1}{24}}&{\frac {1}{6}}\\\hline &P(X=5\wedge Y=1)&P(X=5\wedge Y=2)&P(X=5\wedge Y=3)&P(X=5\wedge Y=4)&P(X=5\wedge Y=5)&P(X=5\wedge Y=6)&P(X=5)\\a_{5}=5&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&{\frac {1}{24}}&0&{\frac {1}{24}}&{\frac {1}{24}}&0&{\frac {1}{24}}&{\frac {1}{6}}\\\hline &P(X=6\wedge Y=1)&P(X=6\wedge Y=2)&P(X=6\wedge Y=3)&P(X=6\wedge Y=4)&P(X=6\wedge Y=5)&P(X=6\wedge Y=6)&P(X=6)\\a_{6}=6&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\parallel \\&0&{\frac {1}{24}}&{\frac {1}{24}}&{\frac {1}{24}}&{\frac {1}{24}}&0&{\frac {1}{6}}\\\hline \hline &P(Y=1)&P(Y=2)&P(Y=3)&P(Y=4)&P(Y=5)&P(Y=6)&\\{\text{Summe}}&\parallel &\parallel &\parallel &\parallel &\parallel &\parallel &\\&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&1\\\hline \end{array}}$$

Spalten- und Zeilensummen

Es gilt stets:
$${\begin{array}{rcrcll}{\text{Für alle}}\ j\in \{1,\ldots ,m\}&:&\sum \limits _{k=1}^{\ell }P(X=a_{j}\wedge Y=b_{k})&=&P(X=a_{j})&{\text{(Spaltensummen)}}\\{\text{Für alle}}\ k\in \{1,\ldots ,\ell \}&:&\sum \limits _{j=1}^{m}P(X=a_{j}\wedge Y=b_{k})&=&P(Y=b_{k})&{\text{(Zeilensummen)}}\\&&\sum \limits _{j=1}^{m}\sum \limits _{k=1}^{\ell }P(X=a_{j}\wedge Y=b_{k})&=&1&{\text{(Gesamtsumme)}}\end{array}}$$

Unabhängigkeit

Definitionsgemäß${\textstyle \;}$sind ${\textstyle X}$ und ${\textstyle Y}$ unabhängig voneinander, falls für alle ${\textstyle j\in \{1,\ldots ,m\}}$ und alle ${\textstyle k\in \{1,\ldots ,\ell \}}$ die Ereignisse ${\textstyle \{X=a_{j}\}}$ und ${\textstyle \{Y=b_{k}\}}$ stochastisch unabhängig voneinander sind, das heißt, falls gilt:
$$P(X=a_{j}\wedge Y=b_{k})=P(X=a_{j})\cdot P(Y=b_{k})$$ $${\text{für alle}}\ j\in \{1,\ldots ,m\}\ {\text{und alle}}\ k\in \{1,\ldots ,\ell \}$$

Beispiele 1

• Die Zahlen ${\textstyle X}$ und ${\textstyle Y}$ auf zwei verschiedenen Laplace-Würfeln sind unabhängig voneinander.

• Die Zahl ${\textstyle X}$ auf der Oberseite und die Zahl ${\textstyle Y}$ auf der Unterseite eines Laplace-Würfels sind nicht unabhängig voneinander.

• Die Zahl ${\textstyle X}$ auf der Oberseite und die Zahl ${\textstyle Y}$ auf der Vorderseite eines Laplace-Würfels sind nicht unabhängig voneinander.

Beispiele 2

• Ist ${\textstyle X}$ die Mathematiknote und ${\textstyle Y}$ die Physiknote eines zufällig ausgewählten Schülers, so sind ${\textstyle X}$ und ${\textstyle Y}$ wohl nicht unabhängig voneinander.

• Ist ${\textstyle X}$ die Mathematiknote und ${\textstyle Y}$ die Anzahl der Geschwister eines zufällig ausgewählten Schülers, so könnten ${\textstyle X}$ und ${\textstyle Y}$ als unabhängig voneinander angenommen werden.

Einzelne und gemeinsame W-Funktion

Zum Zusammenhang zwischen den einzelnen W-Funktionen und der gemeinsamen W-Funktionen:

• Kennt man die gemeinsame W-Funktion zweier ZV, so kann man daraus auf die W-Funktionen der einzelnen ZV schließen.
• Aus den einzelnen W-Funktion zweier ZV kann man jedoch im Allgemeinen nicht auf ihre gemeinsame Funktion schließen. (Die gemeinsame W-Funktion enthält also mehr Informationen als die einzelnen ZV.
• Ist jedoch zusätzlich bekannt, dass zwei ZV unabhängig voneinander sind, so ergibt sich ihre gemeinsame W-Funktion als Multiplikationstabelle aus den einzelnen W-Funktionen.

Linearkombinationen und Verknüpfungen von ZV

1. Ist ${\textstyle X}$ eine endliche ZV und sind ${\textstyle u,v\in \mathbb {R} }$, so ist auch ${\textstyle u\cdot X+v}$ eine endliche ZV.
2. Sind ${\textstyle X,Y}$ endliche ZV, so sind auch ${\textstyle X+Y,\ X-Y}$ und ${\textstyle X\cdot Y}$ endliche ZV.

W-Funktion von Linearkombinationen und Verknüpfungen von ZV I

Ist ${\textstyle X}$ eine endliche ZV, die die Werte ${\textstyle a_{1},\ldots ,a_{m}}$ annehmen kann und sind ${\textstyle u,v\in \mathbb {R} }$ mit ${\textstyle u\not =0}$, so kann die ZV ${\textstyle uX+v}$ die Werte ${\textstyle u\cdot a_{1}+v,\ldots ,u\cdot a_{m}+v}$ annehmen und es gilt: $$P(uX+v=u\cdot a_{k}+v)=P(X=a_{k})\quad {\text{für alle}}\ k=1,\ldots ,n$$

Beispiel 1.1

Ein Laplace-Würfel wird geworfen. Die ZV ${\textstyle X}$ gibt die Zahl auf dem Würfel an. Die ZV ${\textstyle Y}$ gibt die Zahl an, die man erhält, wenn man das Würfelergebnis vervierfacht und dann ${\textstyle 8}$ abzieht, also ${\textstyle Y=4\cdot X-8}$.

Für die W-Funktionen von ${\textstyle X}$ und ${\textstyle Y}$ gilt: $${\begin{array}{c|rcr|rcccl}{\text{mögl. Wert für }}X&{\text{mögl. Wert für }}Y&&&{\text{Wahrscheinlichkeit}}&&\\\hline 1&-4&&&P(Y=-4)&=&P(X=1)&=&{\frac {1}{6}}\\\hline 2&0&&&P(Y=0)&=&P(X=2)&=&{\frac {1}{6}}\\\hline 3&4&&&P(Y=4)&=&P(X=3)&=&{\frac {1}{6}}\\\hline 4&8&&&P(Y=8)&=&P(X=4)&=&{\frac {1}{6}}\\\hline 5&12&&&P(Y=12)&=&P(X=5)&=&{\frac {1}{6}}\\\hline 6&16&&&P(Y=16)&=&P(X=6)&=&{\frac {1}{6}}\end{array}}$$

Beispiel 1.2

Man berechnet daraus:

$$E(X)=3.5\ {\text{und}}\ V(X)=2.9167\quad {\text{sowie}}\quad E(Y)=6\ {\text{und}}\ V(Y)=46.6667$$

W-Funktion von Linearkombinationen und Verknüpfungen von ZV II

Seien ${\textstyle X,Y}$ endliche ZV. Um die W-Funktion von Verknüpfungen von ${\textstyle X}$ und ${\textstyle Y}$ zu ermitteln, muss man die gemeinsame W-Funktion von ${\textstyle X}$ und ${\textstyle Y}$ kennen (es genügt nicht, die einzelnen W-Funktionen von ${\textstyle X}$ und ${\textstyle Y}$ zu kennen).

Ist ${\textstyle \star }$ eine Verknüpfung, so ergibt sich die Wahrscheinlichkeit ${\textstyle P(X\star Y=c)}$ für ${\textstyle c\in \mathbb {R} }$ als Summe der Einzelwahrscheinlichkeiten ${\textstyle P(X=a\wedge Y=b)}$ über alle Kombinationen ${\textstyle (a,b)}$ mit ${\textstyle a\star b=c}$.
$${\text{Also:}}\quad P(X\star Y=c)=\sum \limits _{(a,b),\ a\star b=c}P(X=a\wedge Y=b)$$

Beispiel 2.1

Zwei Laplace-Würfel werden geworfen. Die ZV ${\textstyle X}$ gibt die Zahl auf dem ersten und die ZV ${\textstyle Y}$ gibt die Zahl auf dem zweiten Würfel an. Aus der gemeinsamen W-Funktion von ${\textstyle X}$ und ${\textstyle Y}$ (vgl. 2.1) ermittelt man die W-Funktionen von:

Beispiel 2.2

${\textstyle X+Y}$: $${\begin{array}{c||c|c|c|c|c|c|c|c|c|c|c}c&2&3&4&5&6&7&8&9&10&11&12\\\hline P(X+Y)=c&{\frac {1}{36}}&{\frac {2}{36}}&{\frac {3}{36}}&{\frac {4}{36}}&{\frac {5}{36}}&{\frac {6}{36}}&{\frac {5}{36}}&{\frac {4}{36}}&{\frac {3}{36}}&{\frac {2}{36}}&{\frac {1}{36}}\end{array}}$$
Daraus berechnet man: ${\textstyle \quad E(X+Y)=7}$ und ${\textstyle V(X+Y)=5.8333}$

Beispiel 2.3

${\textstyle X-Y}$:

$${\begin{array}{c||c|c|c|c|c|c|c|c|c|c|c}c&-5&-4&-3&-2&-1&0&1&2&3&4&5\\\hline P(X-Y=c)&{\frac {1}{36}}&{\frac {2}{36}}&{\frac {3}{36}}&{\frac {4}{36}}&{\frac {5}{36}}&{\frac {6}{36}}&{\frac {5}{36}}&{\frac {4}{36}}&{\frac {3}{36}}&{\frac {2}{36}}&{\frac {1}{36}}\end{array}}$$
Daraus berechnet man: ${\textstyle \quad E(X-Y)=0}$ und ${\textstyle V(X-Y)=5.8333}$

Beispiel 2.4

${\textstyle X\cdot Y}$: $${\begin{array}{c||c|c|c|c|c|c|c|c|c}c&1&2&3&4&5&6&8&9&10\\\hline P(X\cdot Y=c)&{\frac {1}{36}}&{\frac {2}{36}}&{\frac {2}{36}}&{\frac {3}{36}}&{\frac {2}{36}}&{\frac {4}{36}}&{\frac {2}{36}}&{\frac {1}{36}}&{\frac {2}{36}}\end{array}}$$
$${\begin{array}{c||c|c|c|c|c|c|c|c|c}c&12&15&16&18&20&24&25&30&36\\\hline P(X\cdot Y=c)&{\frac {4}{36}}&{\frac {2}{36}}&{\frac {1}{36}}&{\frac {2}{36}}&{\frac {2}{36}}&{\frac {2}{36}}&{\frac {1}{36}}&{\frac {2}{36}}&{\frac {1}{36}}\end{array}}$$
Daraus berechnet man: ${\textstyle \quad E(X\cdot Y)=12.25}$

Beispiel 3.1

Ein Laplace-Würfel, bei dem sich die Augenzahlen ${\textstyle 1}$ und ${\textstyle 6}$, sowie ${\textstyle 2}$ und ${\textstyle 5}$ sowie ${\textstyle 3}$ und ${\textstyle 4}$ gegenüberliegen, wird geworfen. Die ZV ${\textstyle X}$ gibt die Zahl auf der Oberseite und die ZV ${\textstyle Y}$ gibt die Zahl auf der Unterseite des Würfels an. Aus der gemeinsamen W-Funktion von ${\textstyle X}$ und ${\textstyle Y}$ (vgl. Gemeinsame Wahrscheinlichkeitsfunktion) ermittelt man die W-Funktionen von:

Beispiel 3.2

${\textstyle X+Y}$:
$${\begin{array}{c||c}c&7\\\hline P(X+Y)=c&1\end{array}}$$
Daraus berechnet man: ${\textstyle \quad E(X+Y)=7}$ und ${\textstyle V(X+Y)=0}$

Beispiel 3.3

${\textstyle X-Y}$:
$${\begin{array}{c||c|c|c|c|c|c}c&-5&-3&-1&1&3&5\\\hline P(X-Y=c)&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}&{\frac {1}{6}}\end{array}}$$
Daraus berechnet man: ${\textstyle \quad E(X-Y)=0}$ und ${\textstyle V(X-Y)=11.6667}$

Beispiel 3.4

${\textstyle X\cdot Y}$:
$${\begin{array}{c||c|c|c}c&6&10&12\\\hline P(X\cdot Y=c)&{\frac {1}{3}}&{\frac {1}{3}}&{\frac {1}{3}}\end{array}}$$
Daraus berechnet man: ${\textstyle \quad E(X\cdot Y)=9.3333}$

Beispiel 4.1

Ein Laplace-Würfel, bei dem sich die Augenzahlen ${\textstyle 1}$ und ${\textstyle 6}$, sowie ${\textstyle 2}$ und ${\textstyle 5}$ sowie ${\textstyle 3}$ und ${\textstyle 4}$ gegenüberliegen, wird geworfen. Die ZV ${\textstyle X}$ gibt die Zahl auf der Oberseite und die ZV ${\textstyle Y}$ gibt die Zahl auf der Vorderseite des Würfels an. Aus der gemeinsamen W-Funktion von ${\textstyle X}$ und ${\textstyle Y}$ (vgl. 2.1) ermittelt man die W-Funktionen von:

Beispiel 4.2

${\textstyle X+Y}$:
$${\begin{array}{c||c|c|c|c|c|c|c|c}c&3&4&5&6&8&9&10&11\\\hline P(X+Y)=c&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {4}{24}}&{\frac {4}{24}}&{\frac {4}{24}}&{\frac {4}{24}}&{\frac {2}{24}}&{\frac {2}{24}}\end{array}}$$
Daraus berechnet man: ${\textstyle \quad E(X+Y)=7}$ und ${\textstyle V(X+Y)=5.8333}$

Beispiel 4.3

${\textstyle X-Y}$:
$${\begin{array}{c||c|c|c|c|c|c|c|c}c&-4&-3&-2&-1&1&2&3&4\\\hline P(X-Y)=c&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {4}{24}}&{\frac {4}{24}}&{\frac {4}{24}}&{\frac {4}{24}}&{\frac {2}{24}}&{\frac {2}{24}}\end{array}}$$
Daraus berechnet man: ${\textstyle \quad E(X-Y)=0}$ und ${\textstyle V(X-Y)=5.8333}$

Beispiel 4.4

${\textstyle X\cdot Y}$:

$${\begin{array}{c||c|c|c|c|c|c|c|c|c|c|c|c}c&2&3&4&5&6&8&12&15&18&20&24&30\\\hline P(X\cdot Y=c)&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}&{\frac {2}{24}}\end{array}}$$ Daraus berechnet man: ${\textstyle \quad E(X\cdot Y)=12.25}$

Rechenregeln für Erwartungswert und Varianz I

Sind ${\textstyle X,Y}$ endliche ZV und sind ${\textstyle u,v\in \mathbb {R} }$, so gilt: $${\begin{array}{|l|l|l|}\hline {\text{stets}}&{\text{stets}}&{\text{stets}}\\E(u\cdot X+v)=u\cdot E(X)+v&V(u\cdot X+v)=u^{2}\cdot V(X)&\sigma _{u\cdot X+v}=|u|\cdot \sigma _{X}\\\hline {\text{stets}}&{\text{falls X,Y unabhängig}}&{\text{falls X,Y unabhängig}}\\E(X+Y)=E(X)+E(Y)&V(X+Y)=V(X)+V(Y)&\sigma _{X+Y}={\sqrt {{\sigma _{X}}^{2}+{\sigma _{Y}}^{2}}}\\\hline {\text{stets}}&{\text{falls X,Y unabhängig}}&{\text{falls X,Y unabhängig}}\\E(X-Y)=E(X)-E(Y)&V(X-Y)=V(X)+V(Y)&\sigma _{X-Y}={\sqrt {{\sigma _{X}}^{2}+{\sigma _{Y}}^{2}}}\\\hline {\text{falls X,Y unabhängig}}&&\\E(X\cdot Y)=E(X)\cdot E(Y)&&\\\hline \end{array}}$$

Rechenregeln für Erwartungswert und Varianz II

Sind ${\textstyle X_{1},\ldots ,X_{n}}$ ZV, so gilt:
$${\begin{array}{|l|rcl|}\hline {\text{stets}}&{\text{falls }}X_{1},\ldots ,X_{n}{\text{unabhängig}}\\E(\sum _{j=1}^{n}X_{j})=\sum _{j=1}^{n}E(X_{j})&V(\sum _{j=1}^{n}X_{j})&=&\sum _{j=1}^{n}V(X_{j})\\&\sigma _{X_{1}+\ldots +X_{n}}&=&{\sqrt {{\sigma _{X_{1}}}^{2}+\ldots +{\sigma _{X_{n}}}^{2}}}\\\hline \end{array}}$$

Aufgabe 1

Zwei sechsseitige Würfel werden geworfen. Die ZV ${\textstyle X}$ gibt das Produkt der Augenzahlen an. Bestimmen Sie die Wahrscheinlichkeitsverteilung von ${\textstyle X}$ und berechnen Sie Erwartungswert und Standardabweichung von ${\textstyle X}$.

Aufgabe 2

Bei der Sendung " Wer wird Millionär? " hat ein Kandidat bereits die Gewinnstufe ${\textstyle 500000}$ Euro erreicht. Bei der nächsten Frage ist er sich mit seiner Antwort zu ${\textstyle 60\%}$ sicher. Antwortet er richtig, erhält er ${\textstyle 1000000}$ Euro, antwortet er falsch, fällt er auf ${\textstyle 16000}$ Euro zurück. Er kann aber auch auf eine Antwort verzichten und hat dann ${\textstyle 500000}$ Euro sicher.

• Berechnen Sie den Erwartungswert für seinen Gewinn, falls er antwortet.
• Diskutieren Sie dann, ob der Kandidat eine Antwort riskieren sollte? (Hierbei gibt es keine eindeutige Lösung.)

Aufgabe 3

In einer Lostrommel befinden sich 8 Kugeln mit den Zahlen ${\textstyle 0,0,0,2,2,5,10,20}$. Bestimmen Sie Erwartungswert und Standardabweichung für die ZV der Summe der gezogenen Zahlen:

• bei einmaligem Ziehen
• bei achtmaligem Ziehen mit Zurücklegen
• bei achtmaligem Ziehen ohne Zurücklegen

Aufgabe 4.1

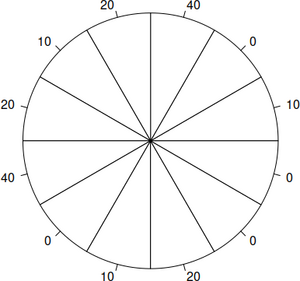
1. Ein Glücksrad (siehe Graphik) wird zweimal gedreht. Die Zahl, die beim ersten Drehen ganz oben steht, wird durch die Zufallsvariable ${\textstyle X}$ beschrieben. Die Zahl, die beim zweiten Drehen oben angezeigt wird, wird durch die Zufallsvariable ${\textstyle Y}$ beschrieben.
Es darf von einem Laplace-Experiment ausgegangen werden.

Aufgabe 4.2

• Bestimmen Sie die W-Funktionen von ${\textstyle X}$ und ${\textstyle Y}$.
• Sind ${\textstyle X}$ und ${\textstyle Y}$ unabhängig voneinander? Bestimmen Sie die gemeinsame W-Funktion von ${\textstyle X}$ und ${\textstyle Y}$.
• Bestimmen Sie Erwartungswert, Varianz und Standardabweichung von ${\textstyle X}$ und ${\textstyle Y}$.
• Es sei ${\textstyle A:=X+Y}$. Welche Werte kann ${\textstyle A}$ annehmen? Bestimmen Sie zur Zufallsvariablen ${\textstyle A}$ die W-Funktion, ${\textstyle E(A)}$, ${\textstyle V(A)}$ und ${\textstyle \sigma _{A}}$.

Aufgabe 4.3

2. Nun betrachten wir den Fall, dass das Rad nur einmal gedreht wird. Die oben stehende Zahl wird durch die ZV ${\textstyle X}$ beschrieben. Die Zahl, die der angezeigten Zahl genau gegenüber liegt, wird durch die ZV ${\textstyle Y}$ beschrieben.

Bearbeiten Sie für diese Situation ebenfalls die Aufgabenteile aus 1.

Aufgabe 5.1

Um die Nutzung einer Aufstiegshilfe für Fische an einer Staustufe (Fischtreppe) zu modellieren, wurde ein Modell entwickelt, bei dem die Anzahl der Fische, die die Aufstiegshilfe innerhalb einer Stunde passieren, bestimmt wird. Die Zufallsvariable ${\textstyle X}$ beschreibe die Anzahl der Fische, die die Aufstiegshilfe innerhalb einer Stunde passieren. Man weiß, dass ${\textstyle X}$ nur die Werte ${\textstyle 0,1,2,3,4,5,6,7}$ und ${\textstyle 8}$ annehmen kann.

Aufgabe 5.2

Wir nehmen an, dass die W-Funktion zur ZV ${\textstyle X}$ bekannt ist und mit nachfolgender Wertetabelle dargestellt werden kann: ${\textstyle X\cdot Y}$: $${\begin{array}{|c||c|c|c|c|c|c|c|c|c|c|c|c|}\hline {\text{Wert}}&k&0&1&2&3&4&5&6&7&8\\\hline {\text{Wahrscheinlichkeit}}&P(X=k)&?&0.26&0.17&0.14&0.09&0.08&0.06&0.04&0.03\\\hline \end{array}}$$

1. Bestimmen Sie die fehlende Wahrscheinlichkeit ${\textstyle P(X=0)}$ für k=0.
2. Berechnen Sie ${\textstyle E(X)}$, ${\textstyle V(X)}$ und ${\textstyle \sigma _{X}}$.
   

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Kurs:Statistik für Anwender' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

• Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
• Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Kurs:Statistik%20f%C3%BCr%20Anwender/Verkn%C3%BCpfung%20diskreter%20Zufallsvariablen
• siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.