OpenSource4School/Lernumgebungen zum Beweisen in der Primarstufe/Gausssche Summenformel

Formale Aspekte

Namen der Verfasser der Lernumgebungsdokumentation

Silke Holz, Nicole Maas, Franziska Krämer

E-Mail-Adressen und Datum

s8siholz@stud.uni-saarland.de, s8frkrae@stud.uni-saarland.de, niha0007@stud.uni-saarland.de; Beginn der Erfassung 29.06.2021

Inhaltsaspekte

Name der Lernumgebung

Auf dem Weg zur Gauß’schen Summenformel: Entdecke das Geheimnis des kleinen Gauß!

Kurzbeschreibung der Lernumgebung

Die didaktische Motivation der Lernumgebung besteht darin, Grundlagen für das formale Beweisen in der weiterführenden Schule zu schaffen und Begründungen für mathematische Regelmäßigkeiten möglichst eigenständig zu finden. Dabei verfolgen die SuS das Ziel, durch elaborierendes Lernen eine oder mehrere mathematische Gesetzmäßigkeiten zu entdecken. Markante Eckpunkte hierbei sind die Erkenntnis der Paarbildung beziehungsweise der Verdopplung der Zahlenreihe in umgekehrter Reihenfolge und die spätere Halbierung. Als Arbeitsmittel und Medien stehen ein Arbeitsblatt mit Aufgabenstellung, Papier (leere Blätter), Stifte in verschiedenen Farben, Wendeplättchen, Zahlkarten, Zahlkarten mit Punkten, Zahlenstrahl, Zahlenstreifen, Zehner-/ Zwanziger- /Hunderterfeld (je nach Abhängigkeit des vorgegebenen Zahlenraumes), Wendeplättchen-App sowie Smartphone, Tablet oder PC zur Verfügung.

Ungefährer Zeitbedarf zur Durchführung

Einzelarbeit: 30 - 45 Minuten

Partnerarbeit bzw. Gruppenarbeit: 45 - 90 Minuten

Adressaten der Lernumgebung

Aufgrund der fachlichen Komplexität ist die Lernumgebung für Kinder ab dem 2./3. Schuljahr ausgelegt.

Bei mathematisch besonders begabten Kindern niedrigerer Klassen kann der Einsatz der Lernumgebung als besondere Herausforderung erprobt werden.

Bei der Wahl eines größeren Zahlenraumes ist die Lernumgebung auch für SuS höherer Klassenstufen eine herausfordernde Angelegenheit. So findet sich das Thema auch in Mathebüchern der 5. Klasse des Gymnasiums im Saarland (Heil et. al., 2013, S. 92).

Zentrale Aufgabenstellungen und Arbeitsaufträge in der Lernumgebung

Thematische Einbettung der Lernumgebung/Einstiegsgeschichte:

Gestern habe ich eine Geschichte aus einer Mathematikstunde von vor über 100 Jahren gelesen. Darin wollte ein Lehrer im Unterricht seine Ruhe vor den Kindern haben und gab ihnen eine Aufgabe, die sie möglichst lange beschäftigen sollte. Die Aufgabe lautete: Addiere alle Zahlen von 1 – 100. Der Lehrer lehnte sich gemütlich in seinem Stuhl zurück und dachte, er könne jetzt gemütlich bis zum Schulschluss entspannen. Da hatte er aber nicht mit dem kleinen Carl- Friedrich Gauß gerechnet. Der war zwar erst 9 Jahre alt, also ungefähr so alt wie du jetzt bist, hatte die Aufgabe aber schon nach wenigen Minuten gelöst (Dahl & Nordqvist 1996, S.37). Heute versuchst du, dem Trick von Carl-Friedrich Gauß auf die Spur zu kommen!

Arbeitsblatt zum Bearbeiten der Lernumgebung:

Explizite Formulierung der Aufgabenstellungen und Arbeitsaufträge:

Aufgabe: Addiere die Zahlen von 1 – 20 möglichst geschickt und beschreibe deinen Lösungsweg. Nutze das Arbeitsblatt für deine Notizen. Gerne darfst du Material aus dem Materialpool zur Unterstützung deiner Ideen nutzen.

Der Zahlenraum 1 – 20 wurde gewählt, damit keine Überforderung der SuS aufgrund einer großen Zahl entsteht. Dieser Zahlenraum kann individuell auf das Niveau der SuS angepasst werden, bspw. auf 1 – 50 oder 1 – 100 bzw. von 1 bis zu einer beliebigen Zahl.

Durchführung der Lernumgebung/Vorgehen:

Der Materialpool wird auf einem Tisch vorbereitet, an dem die SuS sich bedienen können, aber nicht müssen. Sie erhalten zudem das Arbeitsblatt mit dem Arbeitsauftrag und beginnen mit der Bearbeitung. Hierbei wechseln sich Phasen der freien Exploration der SuS und Impulsgebung durch die LP ab bis zur gewünschten Zielerreichung oder Ablauf der zeitlichen Befristung.

Allgemein motivierende Impulse:

• Probiere weiter!

• Überlege noch einmal neu!

• Lass dir Zeit!

• Keine schlechte Überlegung!

• Verfolge deinen Weg weiter!

• Kannst du mir das erklären?

• Erkläre mir dein Vorgehen!

• Wie bist du so schnell auf eine Lösung gekommen? Erkläre es mir.

Weitere mögliche Impulse mit ansteigender Hilfestellung:

• Finde Zahlen, die beim Addieren immer die gleiche Summe ergeben!

• Finde immer zwei Zahlen, die beim Addieren die gleiche Summe ergeben! (SuS entdecken den Aspekt der Paarbildung)

• Finde immer zwei Zahlen, die zusammen 21 ergeben!

• Addiere die erste und die letzte Zahl der Zahlenreihe, dann die zweite und die vorletzte Zahl. Setze das Vorgehen fort!

• Schreibe die Zahlenreihe 1 bis 20 in umgekehrter Reihenfolge unter die Zahlenreihe von 1 bis 20. Beschreibe deine Beobachtung (SuS erkennen die Verdopplung der Zahlenreihe).

• Addiere die untereinander stehenden Zahlen! Was kannst du beobachten? (SuS erkennen, dass Summen immer doppelt vorkommen)

• Setze deine Überlegungen fort und nutze die Multiplikation und Division für die beiden weiteren Rechenschritte (SuS multiplizieren die identischen Einzelsummen mit der Anzahl gleicher Summen; anschließende Halbierung zum Ergebnis).

• Multipliziere die Einzelsummen mit der Anzahl der übereinstimmenden Summen und halbiere das Ergebnis.

Impuls bei einer eigenständigen Lösung des SuS:

• Gilt deine Beobachtung/Regel/Vorgehen denn immer? Auch bei einer ungeraden Zahl?

Technische Voraussetzungen

Soll das Tablet bzw. die Wendeplättchen-App (s. Potenzial des Einsatzes digitaler Medien) als digitales Arbeitsmittel zum Einsatz kommen dürfen, muss die dafür erforderliche Infrastruktur gegeben sein. Das heißt, Tablets und ein Internetzugang zur Verwendung der App müssen zur Verfügung stehen.

Im Idealfall stehen so viele Tablets, wie SuS in der Klasse sind, zur Verfügung, da sich im Zweifelsfall alle SuS für dieses Arbeitsmittel entscheiden werden. Steht nur ein Tablet zur Verfügung, kann auch das Los zwischen allen interessierten SuS entscheiden.

Mathematischer Gehalt der Lernumgebung

Mathematische Analyse

Eine Voraussetzung für den Einsatz der Lernumgebung ist, dass die SuS eine Zahl als Kardinalzahl sicher kennen und hinter einer symbolisch präsentierten Zahl eine Menge verstehen. Die Kinder sollten sich mindestens im Zahlenraum bis 20, besser im Zahlenraum bis 100 sicher bewegen und die Addition von Zahlen in diesen Zahlenräumen beherrschen. Außerdem sollten sie Grundkenntnisse in der Multiplikation und Division (hier: verdoppeln/halbieren) haben.

Mögliche Lösungswege:

https://commons.wikimedia.org/wiki/File:Verschiedene_M%C3%B6glichkeiten_der_Paarbildung_1.jpg https://commons.wikimedia.org/wiki/File:M%C3%B6glichkeit_der_Paarbildung_%C3%BCber_das_Zwanzigerfeld.jpg

Mathematikdidaktischer Gehalt der Lernumgebung

Didaktische Analyse

Folgende Befunde zu Vorgehensweisen bzw. typischen Fehlern/ Hindernissen gibt es in der Literatur:

• Kardinalzahlaspekt

• Zählendes Rechnen

• Rechenfehler

• Kraft der Fünf anstatt Teilbarkeit durch zwei

• Festhalten an zuvor eingeübten Strukturierungshilfen

• Fortwährende Motivation der SuS durch die Lehrperson, falls der SuS zu wenig oder nicht eigenständig nach einer Lösung sucht

• Zeit zum eigenständigen Überlegen lassen von Seiten der Lehrperson

„Gute“ Aufgaben & Differenzierung

Bei der gewählten Aufgabenstellung der Lernumgebung handelt es sich um eine herausfordernde Aufgabenstellung, die zur kognitiven Aktivität jedes SuS beiträgt. Es handelt sich um die Form einer äußeren Differenzierung, da einerseits der Zahlenraum der Aufgabe dem Niveau angepasst werden kann und die LP Steuerung in der Bereitstellung der Hilfsmittel und Impulsgebung übernehmen kann. Die natürliche Differenzierung ist dadurch gegeben, dass der SuS selbst entscheidet, welche Hilfsmittel er für seinen Lösungsweg wählt und unter Umständen auch, wann er sich weitere Hilfen einfordert. Dies ist wiederum davon abhängig, wie der SuS sich auf die Bearbeitung der Lernumgebung einlässt. Sind die SuS offenes und selbständiges Lernen gewöhnt, wird die LP ggf. weniger Impulse geben müssen. Haben die SuS hingegen wenig Erfahrung im eigenständigen und offenen Lernen, wird die LP entsprechend öfter intervenieren müssen und durch geeignete Impulse steuern.

Artikulation, Kommunikation, Soziale Organisation

Die SuS dürfen alle Artikulationsoptionen nutzen und werden explizit zur Beschreibung des Lösungsweges aufgefordert, der dann auf dem Arbeitsblatt schriftlich festgehalten wird. Handelt es sich bei dem SuS um einen SuS, der Schwierigkeiten beim Schreiben aufgrund des Alters oder sonstiger Beeinträchtigungen aufweist, empfiehlt es sich die Beschreibung des Lösungsweges auch als Audio-Datei festzuhalten, um eine mögliche Reflexion anschließen zu können.

Den SuS wird bei der Bearbeitung ihrer Aufgabe immer wieder Zeit zum eigenständigen Überlegen und Ausprobieren gelassen. Dabei sind vielfältige Möglichkeiten zur Gestaltung gegeben. Der Kreativität der Kinder werden keine Grenzen gesetzt. Um das Behalten und die Vertiefung der Gedankengänge zu fördern, werden die SuS immer wieder aufgefordert, ihren Lösungsweg durch Notizen jeder Art nachvollziehbar zu machen. Kommen SuS in ihren Überlegungen zu einer möglichen Lösung nicht weiter, muss die LP durch angemessene Impulse neue Denkanstöße anregen. Eine Reflexion über die jeweiligen Gedankengänge bzw. über die Problemstellen der Aufgabe findet im Anschluss an die Bearbeitung der Lernumgebung statt.

Die Lernumgebung kann in Einzelarbeit, Partnerarbeit oder Gruppenarbeit in Kleingruppen eingesetzt werden. Die Erprobung der Lernumgebung fand in einer Gruppe von 4 SuS in einer 3. Klasse statt.

Potenzial des Einsatzes (digitaler) Medien

Materialpool (zur Differenzierung können die Kinder ihr Material individuell auswählen):

• Wendeplättchen, https://commons.wikimedia.org/wiki/File:Wendepl%C3%A4ttchen_und_Zahlenkarten_mit_Punkten.jpg

• Zahlenkarten mit numerischer/ ikonischer/ kombinierter Darstellung, https://commons.wikimedia.org/wiki/File:Wendepl%C3%A4ttchen_und_Zahlenkarten_mit_Punkten.jpg

• Tablet/Smartphone/PC mit Wendeplättchen App, https://www.melanie-platz.com/WPA/Wendeplaettchen.html

• Zahlenstrahl (mit symbolischer/ikonischer Darstellung), https://commons.wikimedia.org/wiki/File:Zahlenstrahl_bis_20.jpg

• Zahlenstreifen, https://commons.wikimedia.org/wiki/File:Zahlenstreifen_bis_20.jpg

• Zehner-/ Zwanziger-/ Hunderterfeld

Wird die Lernumgebung gleichzeitig mit mehreren Kindern durchgeführt, muss theoretisch für alle SuS das gesamte Material zur Verfügung stehen, da sich die Kinder oft zunächst von optischen Reizen leiten lassen. Somit ist es sehr wahrscheinlich, dass viele SuS sich anfänglich für das Tablet als Medium entscheiden werden, vor allem dann, wenn die SuS noch nicht oft im Unterricht damit arbeiten durften. Dieser Umstand könnte bei einer großen SuS-Gruppe für die Umsetzung der Lernumgebung sehr investiv, also teuer, werden.

Das Benutzen des Materials wird den Kindern vor dem Beginn des Lernens erklärt und freigestellt. Unklarheiten bezüglich der Nutzung werden vorab im Plenum geklärt.

Als konsumtives Material werden Papier für Notizen, Stifte und das Arbeitsblatt mit Aufgabenstellung benötigt.

Das Material wird als „Pool“ auf einem Materialtisch bereitgestellt.

Dies bringt den großen Vorteil mit sich, dass die Kinder offen bezüglich der Verwendung und Auswahl des Materials sind.

Nachteile sind beispielsweise, dass viele Kinder digitale Materialien um der Sache wegen bevorzugen, obwohl kein Mehrwert zu erwarten ist oder sie in dem Umgang noch nicht sehr geübt sind. Außerdem muss bei Durchführung in einer Klasse das Material in mehrfacher Ausführung vorhanden sein.

Die Arbeitsmittel und Medien erfüllen die unterstützende Funktion zur Visualisierung von Sachverhalten.

Sie bringen folgende fachdidaktischen Potenziale mit: Auf Basis des EIS- Prinzip nach J. Bruner werden enaktive Handlungen ermöglicht und es kann ein individueller Übergang zu ikonischer und symbolischer Handlungsweise entstehen.

Für die Lernumgebung werden vornehmlich Materialien eingesetzt, die entweder in der Schule bereits vorhanden sind, oder mit geringem Aufwand selbst erstellt werden können. Daher ist das Preis-Leistungs-Verhältnis ausgewogen, sofern nicht noch Tablets und Internetzugang bereitgestellt werden müssen.

Bezüglich der Zuwendung der Lehrperson lässt sich feststellen, dass die Lernumgebung ohne gezielte Impulse durch die LP wahrscheinlich schwer umsetzbar ist. Ein erstes Explorieren funktioniert sicher auch im Austausch mit den SuS, aber die Beweisführung gelingt wahrscheinlich nur durch geschickte Impulsgebung.

Evaluation

Als Strategiedokument dient das zur Lernumgebung erstellte Arbeitsblatt mit enthaltener Aufgabenstellung (s. Zentrale Aufgabenstellungen und Arbeitsaufträge in der Lernumgebung), sofern die SuS dieses auch zur Bearbeitung der Lernumgebung nutzen und ihren Lösungsweg darauf dokumentieren. Die LP hat Möglichkeiten die SuS individuell weiterzuführen, indem sie ihnen gezielte Impulse gibt. Diese Impulse der LP können soweit gesteuert werden, bis die SuS zu einer Lösung kommen. Sollen die Gedankengänge der SuS zu einem späteren Zeitpunkt vertieft werden, ist dies ebenso möglich.

Alle Schülerlösungen sollten grundsätzlich durch den Nachvollzug der Lehrperson gewürdigt werden. Dabei sollten Lösungsansätze, die nicht zielführend sind, durch Impulse zu problemlösenden Strategien in die richtige Richtung gelenkt werden. SuS mit zielführenden Lösungsansätzen sollten motiviert werden, weiter in diese Richtung zu forschen. Nur so hat die LP die Chance Einblick in das Denken der SuS zu erlangen und durch geeignete Impulse den SuS gezielt zu fördern und weiterzuführen.

In dieser Lernumgebung findet soziales Lernen statt, sofern ein Austausch über die Entdeckungen in irgendeiner Form stattfindet. In der Sozialform Partnerarbeit entsteht durch den gemeinsamen Austausch und Überlegungen an der Aufgabe soziales Lernen. Wird die Lernumgebung in Einzelarbeit durchgeführt, findet soziales Lernen durch anschließendes Erklären oder Berichterstattung zu den Entdeckungen des SuS in einer Mathekonferenz statt.

Vernetzung mit anderen Lernumgebungen

• In Verbindung mit der vorliegenden Lernumgebung sind Lernaktivitäten in folgenden Bereichen denkbar: Zahlentreppen, Zahlenreihen, Addieren von Dreierzahlen, gegensinniges Verändern, Dreieckszahlen. Als vorgeschaltete Übung wären „Schöne-Päckchen”- Aufgaben denkbar, wie z. B.: Rechne und setze fort!

5 + 1 =

4 + 2 =

3 + 3 =

2+ .. =

• Die Lernumgebung bietet Verknüpfungen und Ansätze zu der Leitidee „Raum und Form“ durch die geometrische Herangehensweise der Beweisführung (ikonisch und enaktiv) sowie zu der Leitidee „Muster und Strukturen“ durch die arithmetische und geometrische Herangehensweise der Beweisführung (symbolisch, ikonisch und enaktiv).

• Eine fächerübergreifende Verbindung der Thematik zu anderen Fächern der Grundschule ist möglich. Zum Fach Deutsch, indem die Beweisführung und Begründung versprachlicht, argumentiert und aufgeschrieben wird. Zum Sachunterricht besteht eine Verbindung durch die wahre Geschichte des kleinen Gauß, der herausragende Denkleistungen vollbrachte und ein bedeutender Mathematiker war. Hier ist der Bezug zur historischen Perspektive des Sachunterrichts gegeben.

• Beziehungen zur außerschulischen Lebenswelt: Das Wissen um die Gauß’sche Summenformel ist im Alltag wenig von Relevanz. Dennoch kann ein SuS eine andere Person verblüffen, wenn er das Wissen nutzt und ein Spiel daraus macht, wie z. B.: „Ich wette, dass ich die Summe der Zahlen von 1 bis 20 (oder individuell gewählte Zahl) schneller addieren kann, als du sie in den Taschenrechner eingeben kannst.“ Die Gauß’sche Summenformel ist immer dann von Bedeutung, wenn es um eine linear ansteigende Menge geht, die immer um die Vorgängerzahl plus 1 wächst. Auf die Praxis angewandt, kann man so berechnen, wie viele Blockstufen für eine Treppe benötigt werden, wenn die Steine nicht irgendwo aufgelegt werden, sondern nacheinander aufgestapelt werden. Wenn eine Stufe beispielsweise eine Tiefe von 25 cm hat und eine Treppe mit einer Grundlänge von 2 m entstehen soll, werden [8*(8+1)/2], also 36 Blockstufen, benötigt. Aus Kostengründen wird eine Treppe in der Realität aber nicht so gebaut werden, da die Blockstufe im Vergleich zu Schotter als Füll- und Unterbaumaterial viel zu teuer ist.

Reflexion der Lernumgebung

Mögliche Stolpersteine:

Der Materialpool zur Lernumgebung könnte für manche SuS zur Herausforderung werden und einige SuS ggf. überfordern. Hier kann es möglich sein, dass die LP den SuS auffordert sich für etwas zu entscheiden und erst mal auszuprobieren. Ist tatsächlich eine Überforderung zu erkennen, sollte die LP die Materialauswahl eingrenzen oder dem SuS ein Arbeitsmittel zuteilen und dem SuS somit diese Entscheidung abzunehmen. Durch eine mögliche Überforderung könnte die Motivation zum Arbeiten in der Lernumgebung schlagartig verloren gehen.

Wann sollte die Lernumgebung nicht angewendet werden?

Die Lernumgebung ist ungeeignet für Kinder, die noch nicht den kardinalen Zahlaspekt verinnerlicht haben und noch nicht mit dem entsprechenden Zahlenraum vertraut sind (s. Mathematische Analyse).

Nach der Durchführung

Daten zur Durchführung

Die Lernumgebung wurde am 02.07.2021 in einer Kleingruppe als Gruppenarbeit von vier SuS der 3. Klassenstufe an einer Frankfurter Grundschule durch die dortige Korrespondentin erprobt.

Zur Durchführung der Lernumgebung stand der Gruppe lediglich ein Zeitfenster von 30 Minuten zur Verfügung.

Schülerdokumente

Reflexion

Rückblickend wäre die Lernumgebung aus unserer Sicht und aus Sicht der Frankfurter Studentin nicht mit einer Vorschulklasse durchführbar gewesen. Nach Aussagen der Frankfurter Studentin war es auch sinnvoll, die Lernumgebung in einer Gruppenarbeit durchzuführen, da sich die Kinder untereinander ausgetauscht, ihre Ergebnisse zusammengefasst und gemeinsame Lösungswege gesucht haben.

Aus dem Materialpool wurde der Zahlenstrahl bis 20 als Hilfsmittel von allen Kindern bevorzugt. Es muss allerdings erwähnt werden, dass der Materialpool nicht vollständig aufgebaut wurde. Hier wurden beispielsweise die Zahlenkarten mit den Punkten und auch die Zahlenstreifen nicht ausgeschnitten zur Verfügung gestellt und stellten somit für die Kinder kein attraktives Hilfsmittel dar. Es fehlten zudem das Zwanzigerfeld, Wendeplättchen und auch das Tablet in der Materialauswahl. Somit war die Wahl der Hilfsmittel stark eingegrenzt. Die eigene Erprobung der Lernumgebung zu einem späteren Zeitpunkt wird sicher neue Erkenntnisse zur Materialbereitstellung und SuS-Reaktionen bringen.

Durch Impulsgebung sind die SuS von ihrem anfänglichen Weg „mal“ zu rechnen (Multiplikation), zurück zur Addition geführt worden und haben dann relativ schnell den Weg der Paarbildung für sich als Möglichkeit entdeckt. Hierbei haben sie zunächst die Summenbildung zur 20 gewählt, was zu einem kognitiven Konflikt führte, da für die 10 und die 20 kein Partner zur gleichen Paarbildung übrig blieb. Mit dem Hinweis, dass es ja nicht unbedingt 20 sein müssen und der Erfahrung aus den Überlegungen davor, wurde die 21 in diesem Fall als zielführend ermittelt.

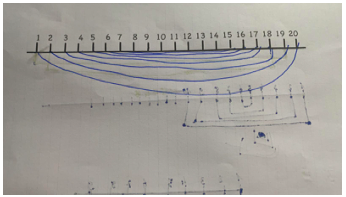
Die Zuordnung der Paare erfolgte durch Verbindung mittels eines Bogens. Die SuS bezeichneten die Bögen als „Regenbogen“, der ihnen bei der Visualisierung geholfen hat. Mit dieser Methode haben die SuS einen Weg gefunden gerade Zahlen möglichst geschickt zu addieren. Die Überlegung, ob das auch so bei ungeraden Zahlen funktioniert, wurde von der betreuenden Studentin initiiert. Hierbei waren die SuS erneut sehr kreativ und haben die Zahl 0 am Zahlenstrahl ergänzt, so dass wieder eine gerade Anzahl an Positionen entstand und die Paarbildung wieder möglich wurde. Hier wurde die Erprobung leider aus zeitlichen Gründen beendet.

Weitere Überlegungen wären gewesen, wie praktikabel die Methode bei größeren Zahlen ist und ob es noch eine andere Methode gibt, schneller auf die Summe der Zahlen zu kommen. Hier hätte man auf die Verdopplung der Zahlenreihe in umgekehrter Reihenfolge mit anschließender Addition der Einzelsummen und Halbierung der Menge abzielen können, bevor die Kinder aus diesem Vorgehen ggf. auf eine Allgemeingültigkeit schließen können. Erst danach wäre ein formaler Beweis möglich. Das sind allerdings Überlegungen, die im Sinne des Spiralcurriculums zu einem späteren Zeitpunkt wieder aufgegriffen werden könnten, um die Kinder in ihren Erkenntnissen weiterzuführen.

Literatur

Meyer, M. & Prediger, S. (2012). Warum? Argumentieren, Begründen, Beweisen. Praxis der Mathematik in der Schule, 30(51), 1-7.

https://www.mathematik.uni-dortmund.de/~prediger/veroeff/09-Meyer_Prediger_PM-H30-Argumentieren-Webversion.pdf

Dahl, K. & Nordqvist, S. (1996). Zahlen, Spiralen und magische Quadrate. Hamburg: Verlag Friedrich Oetinger. S. 37-39.

Stewart, I. (2008). Die Macht der Symmetrie. Warum Schönheit Wahrheit ist. Berlin, Heidelberg: Springer Spektrum. S. 64-66.

Heil, H.; Rau, R. & Ulma, H. (2013). Mathematik 5, Gymnasium G8. Rechengesetze. Grundbegriffe der Mathematik. Saarbrücken: Softfrutti Verlag.

https://www.melanie-platz.com/WPA/Wendeplaettchen.html