Projekt:Tabellenkalkulation
Tabellenkalkulations-Know-How
[Bearbeiten]In diesem Projekt sammeln wir Grundkonzepte, Problemlösungen und Tipps & Tricks zum Thema "Tabellenkalkulation".
Aufbau von Kalkulationsblättern
[Bearbeiten]Zeilen, Spalten, Zellen
[Bearbeiten]Koordinatensysteme für Tabellen
[Bearbeiten]Daten in Zellen
[Bearbeiten]Texte
[Bearbeiten]Wahrheitswerte
[Bearbeiten]numerische Werte
[Bearbeiten]Fetter Text===== Formeln===== FetterFetter Text Text
Zellbezüge
[Bearbeiten]Beispiele
[Bearbeiten]Beispiel 1
[Bearbeiten]Prozente berechnen
 |
 |
Beispiel |
Beispiel 2
[Bearbeiten]Optimierungsaufgabe
Rechnen mit der Tabellenkalkulation
[Bearbeiten]Will man, dass in einer Zelle ein Wert berechnet wird, so beginnt die Eingabe mit dem zeichen =. Alle Einträge, die mit dem zeichen = beginnen heißen Formeln.
Was sind absolute und relative Zellbezüge?
[Bearbeiten]Was bedeutet eigentlich, dass sich eine Zelle auf eine andere bezieht: der Wert der anderen Zelle wird verwendet. Jede Zelle hat eine genaue Spalte und eine genaue Zeile.
Beispiel A1 B2 C3 D1 F5
Wenn man einen Zellbezug eingibt kann man dies Per Tastatur eingeben das heißt A1 B2 C3 D1 F5 davor muss allerdings immer ein "=" stehen,. Oder man schreibt ein "=" und klickt danach mit der Maus auf die Zellen auf die man sich in seiner Zelle beziehen will.
Hierbei wird zwischen relativen und absoluten Bezügen unterschieden. Standardmäßig werden relative Bezüge verwendet. Der Unterschied wird erst beim Kopieren von Formeln deutlich.
relative Bezüge
[Bearbeiten]Zur Klärung des Begriffs "relativer Zellbezug" beziehen wir uns auf Beispiel 1. In den Zellen von B4 bis B16 werden Prozentwerte berechnet. Alle diese Prozentwerte beziehen sich auf den Grundwert 3178 € in Zelle D1. Die entsprechenden Prozentsätze sind in den Zellen A4 bis A16 eingetragen. Jede Zelle, die einen Prozentwert berechnen soll findet ihren (persönlichen) Prozentsatz in der Zelle links neben ihr. Die Formeln in B4 bis B16 rechnen also nach folgendem Schema: Multipliziere den Wert deines linken Nachbarn mit dem Grundwert.
Formeln können ebenso wie Zahlen und Texte kopiert werden: erst kopieren, dann einfügen. Bei der Tabellenkallkulation wird allerdings nicht nur die Formel kopiert, das Programm passt die Formel dabei an die nächste Zelle an. Beispiel: in B1 steht "A1*5" wird dies nun in B2 kopiert wird die Formel zu "A2*5" wird dies nun in B3 kopiert wird die Formel zu "A3*5"
Eine Formel enthält dann einen relativen Zellbezug wenn sie besagt, wie viele Zeilen oder Spalten man nach rechts, links, oben oder unten gehen soll.
Steht in der Zelle B6 die Formel =B5+3 (in B5 steht 4), so erscheint in B6 das Ergebnis der Zahl aus B5 mit 3 addiert, also 7.
Kopiert man diese Formel in B7 bis B10, so erscheint in B7 die Formel =B6+3 ("gehe eine Zeile nach oben und addiere 3"). Hier erscheint daher 10.
So wird die Reihe immer fortgesetzt, sodass in B10 die Zahl 19 erscheint.
Würde in B6 die Formel =B5*2-2 stehen, so erscheint in B7 als Ergebnis die Zahl 6. B8 enthält die Zahl 10, B9 die 18 und B10 die 34.
absolute Zellbezüge
[Bearbeiten]Will man nun allerdings in jeder dieser Zellen "A1 *5" stehen haben, muss ein absoluter Zellbezug verwendet werden. Dazu muss den Zellbezugelementen (Buchstabe und Zahl) jeweils ein "$"-Zeichen vorangestellt werden. Dabei muss man beachten, dass sowohl die Spalte als auch die Zeile bezeichnet werden muss. Beispiel: $A$1*5 Wenn man dies nun in die anderen Zellen kopiert bleibt die Formel unverändert.
Modelle
[Bearbeiten]Das Drei-Ebenen-Modell
[Bearbeiten]Um die Tabellenkalkulation besser zu verstehen, gliedert man sie in 3 Ebenen auf; die Formelebene, die Werteebene und die Darstellungsebene. In der Formelebene stehen die eingegebenen Formeln bzw. alphanumerische Zeichen. Die Werteebene enthält die ungerundeten ausgerechneten Werte aus der Formelebene oder die alphanumerischen Zeichen falls es sich nicht um eine Formel handelt. Angezeigt werden die Werte dann in der Darstellungsebene, in der sie je nach Formatierung gerundet und/oder in bestimmte Einheiten umgewandelt werden.
Das Pfeilmodell
[Bearbeiten]Durch das Einzeichnen von Pfeilen werden die Beziehungen zwischen Zellen visualisiert. (Excel 2007 und 2010 Formeln->Formelüberwachung->Spur zum Vorgänger/Nachfolger, Excel 2003 und OpenOffice Extras->Detektiv->Spur zum Vorgänger/Nachfolger) Pfeilmodell
Farbmodell
[Bearbeiten]Generierung von Zellbezügen
[Bearbeiten]Es gibt prizipiel zwei Methoden Zellenbezüge zu generieren, erstens man "zeigt" durch Mausklick auf welche Zellen sich bezogen werden soll oder zweitens man kopiert den Inhalt von Zellen die bereits Zellenbezüge beinhalten, dies geschieht meistens durch "nach unten" ausfüllen (siehe Methoden CCP).
Der Zeigemodus
[Bearbeiten]Beim Zeigemodus wird in die Zelle direkt eingetragen auf welche anderen Zellen sich bezogen werden soll. Zuerst wird ein "=" eingegeben dann die Zelle angeklickt auf die sich bezogen werden soll und die Rechenoperation mit der sie verknüpft ewerden soll eingegeben, dann wird die nächste Zelle angeklickt und wenn alles eingetippt ist erhält man durch drücken der "Enter" Taste das Ergebnis. Statt die gewünschten Zellen anzuklicken kann auch ihr Name eingegeben werden oder man kann sie mit den Pfeiltasten ansteuern. Ein solche Zelle mit direkt generierten Zellenbezügen ist nornmalerweise der Beginn eines Tabellenblattes und es wird im Anschluss auf diese Zelle aufgebaut in dem sie immer wieder kopiert und eingefügt wird. Generieren wir Zellenbezüge auf die zuvor beschriebene Art und kopieren sie dann wird sich in der neu eingefügten Zelle nicht auf die Zelle bezogen auf die sich die Ausgangszelle bezogen hat sondern auf die jenige die von der neuen Zelle den selben Abstand nach oben und zur Seite hat (z.B. wie in den folgenden Bildern: 1.Bezug: eins nach rechts und zwei nach oben, 2. Bezug: zwei nach rechts und zwei nach oben). Denn dies sind die so genannten relativen Zellenbezüge.
Wollen wir aber das die eingefügte Zelle sich auf die selbe Zelle bezieht wie die Ausgangszelle müssen wir einen absoluten Zellenbezug generieren. Dies gelingt, wenn man beim eingeben der Formel auf die Zelle klickt auf die sich absolut bezogen werden soll und "f4" drückt. Stellt man zum Beispiel einen absoluten Zellenbezug zu B1 her erscheint "$B$1" in der Formel (alternativ kann man auch die "$" manuell eingeben). Ergänzung: Durch mehrmaliges Drücken von "f4" lassen sich gemischte Zellenbezüge generieren.
Methoden CCP
[Bearbeiten]CCP steht für "Cut" (Ausschneiden), "Copy" (Kopieren) and "Paste" (Einfügen). Hier geht es also um das Kopieren oder auch Ausschneiden und an anderer Stelle wieder Einfügfen von Zellen. Dies kann über gewöhnliches ausschneiden und einfügen erfolgen in "Exel" wird es aber hauptsächlich über unten (bzw. rechts, links oder oben) ausfüllen gemacht. Dies kann auf verschiedene Arten erfolgen.
1. Menü
Zellenbezüge lassen sich leicht über das Menü kopieren und einfügen, dafür klickt man auf die Zelle deren Inhalt kopiert werden soll und zieht mit dem Cursor über die Zellen in die eibgefügt werden soll. Danach wählt man im Menü, Bearbeiten und dort den Unterpunkt Ausfüllen dort kann man dann die gewünschte Richtung (von der Zelle aus deren Inhalt kopiert wird) wählen in die kopiert werden soll.
2. Tastenkombinationen
Eine schnellere Variante sind die Tastenkombinationen. Zunächst wird verfahren wie bei 1. doch statt dann Ausfüllen im Menü zu wählen wird einfach eine Tastenkombination gedrückt.
Tastenkombinationen für die verschiedenen Richtungen:
- unten ausfüllen: "strg" + "u";
- oben ausfüllen: "strg" + "o";
- rechts ausfüllen: "strg" + "r";
- links ausfüllen: "strg" + "l";
3. "Zieh" Methode
Eine weitere Möglichkeit Zellenbezüge zu generieren ist die "Zieh" Methode. Man klickt auf die rechte untere Ecke der Zelle, deren Inhalt kopiert werden soll, und hält die linke Maustaste gedrückt und zieht dann den Cursor über die Zellen in die eingefügt werden soll. Lässt man die linke Maustaste los werden diese Zellen mit Inhalt gefüllt.
Zellbezeichnugsarten und Zellbezüge
[Bearbeiten]Excel verfügt über zwei Bezugsarten:
1.) A1-Bezugsart (Spalte/Zeile)
2.) Z1S1-Bezugsart (Zeile/Spalte).
Spalte/Zeile
[Bearbeiten]Hier geht es um die A1-Bezugsart. Bei dieser Bezugsart werden die Spalten mir Buchstaben (A, B, C,…) bezeichnet, die Zeilen werden nummeriert (1, 2, 3,…).
Der Bezug auf eine Zelle wird in der Form „<Spaltenbuchstabe><Zeilennummer>“ geschrieben. Somit bezeichnet man die erste Zelle mit A1, d.h. A entspricht die erste Spalte, 1 entspricht die erste Zeile (rot).
Weitere Beispiele:
Zelle B3, d.h. B entspricht die zweite Spalte, 3 entspricht die dritte Zeile (blau).
Zelle C5, d.h. C entspricht die dritte Spalte, 5 entspricht die fünfte Zeile (grün).
Man unterscheidet zwischen relativen und absoluten Zellbezügen, siehe http://de.wikiversity.org/wiki/Projekt:Tabellenkalkulation#Was_sind_absolute_und_relative_Zellbez.C3.BCge.3F
Zeile/Spalte
[Bearbeiten]Hier geht es um die Z1S1-Bezugsart. Bei dieser Bezugsart werden sowohl Zeilen als auch Spalten nummeriert (1, 2, 3,…).
Der Bezug auf eine Zelle wird, anders wie bei der A1-Bezugsart, in der Form „Z<Zeilennummer>S<Spaltennummer>“ geschrieben.
Somit bezeichnet man die erste Zelle mit Z1S1 (erste Zeile, erste Spalte - rot).
Weitere Beispiele:
Zelle Z2S3 (zweite Zeile, dritte Spalte - blau);
Zelle Z3S5 (dritte Zeile, fünfte Spalte - grün).

Man unterscheidet zwischen relativen und absoluten Zellbezügen.
Relative Zellbezüge können, genauso wie bei der A1-Bezugsart, durch den Zeigemodus erzeugt werden ODER über die Tastatur angegeben werden. In einer Formel geben sie die genaue Adresse einer Zelle an, basierend auf der relativen Position der Zelle, die die Formel enthält. Relative Zellbezüge bei der Z1S1-Bezugsart sind wie folgt zu deuten:
a) ZS(2) :
1. Z => bleibe in derselben Zeile;
2. S(2) => gehe 2 Spalten nach rechts.
b) Z(-1)S(3):
1. Z(-1) => gehe 1 Zeile nach oben;
2. S(3) => gehe 3 Spalten nach rechts.
c) Z(1)S(-2):
1. Z(1) => gehe 1 Zeile nach unten;
2. S(-2): => gehe 2 Spalten nach links.
d) Z(1)S:
1. Z(1) => gehe 1 Zeile nach unten;
2. S => bleibe in derselben Spalte.
Beispiel:
Wir möchten die Summe zweier Zahlen berechnen.
Summe=ZS(-2)+ZS(-1). Das bedeutet:
1. Schritt: ZS(-2)
bleibe in derselben Zeile; gehe 2 Spalten nach links; nimm diese Zahl als erste Ziffer
2. Schritt: ZS(-1)
bleibe in derselben Zeile; gehe 1 Spalte nach links; nimm diese Zahl als zweite Ziffer
3. Addiere die beiden Zahlen.
Absolute Zellbezüge werden NUR über die Tastatur in der Form „Z<Zeilennummer>S<Spaltennummer>“ angegeben. In einer Formel geben sie die genaue Adresse einer Zelle an, unabhängig von der Position der Zelle, die die Formel enthält.
Bei der Berechnung der Mehrwertsteuer wird z.B. die Zelle Z2S4 über die Tastatur als absoluter Zellbezug angegeben.

Didaktischer Vergleich der Bezeichnungarten bezüglich der Zellebezüge
[Bearbeiten]Ein Vorteil bei der Z1S1-Bezugsart (links) ist, dass sich die Darstellung einer Formel durch Kopieren nicht ändert. Dadurch wird es um so deutlicher, was gemeint ist, wenn wir von relativen Zellbezügen sprechen.
Der Nachteil ist, dass man nicht unmittelbar sieht, welche Zellen in einer Formel verwendet werden, im Gegensatz zu der A1-Bezugsart (rechts).
Das Überprüfen von Formeln wird schwierig, da eine Excel-Tabelle mehrere Daten/Angaben/Werte und Formeln beinhaltet.
Heranführung von Schülern an die Verwendung von Zellbezügen
[Bearbeiten]Geeignete Beispiele für die Einführung von relativen und absoluten Zellbezügen
[Bearbeiten]Beispiel 1
[Bearbeiten]Beispiel 2
[Bearbeiten]| Hier gibt es einen relativen und absoluten Zellbezug. Der absolute Zellbezug findet sich in Zelle C3, der relative Zellbezug in den Zellen B6 bis B16. |
Beispiel 3
[Bearbeiten]Beispiel 4
[Bearbeiten]| In der C-Spalte befindet sich eine Wenn-Dann-Funktion. Es erscheint "Einlass", wenn die Person über 18 ist und "kein Einlass", wenn die Person unter 18 ist. |
Merkmale geeigneter Beispiele
[Bearbeiten]- Die Aufgaben sollten für die Schüler motivierend sein, d.h. in irgendeiner Weise einen Bezug zum Leben der Schüler haben. (z.B. Kosten einer Klassenfahrt berechnen, Wechselkurstabelle für den Auslandsaufenthalt erstellen, Verdienst aus einem Ferienjob berechnen,...)
- Die Aufgaben sollten so gestellt sein, dass es Sinn macht, dass man die Tabellenkalkulation nutzt und nicht einfach alles mit dem Taschenrechner berechnet.
- Die Aufgaben sollten zeigen, dass es sinnvoll ist, die Tabellenkalkulation auch außerhalb der Schule zu nutzen, um sich lästige Rechenarbeit zu sparen.
- Hat man eine Datei "perfektioniert", kann man diese immer wieder für neue Daten übernehmen und spart somit Zeit, die man dann mit Freizeitaktivitäten füllen kann.
Festigung und Vertiefung des Verständnisses für Zellbezüge
[Bearbeiten]Schüler "spielen Tabellenkalkulation"
[Bearbeiten]Wie der Name schon sagt spielen bei dieser Übung die SuS eine ausgearbeitete Tabellenkalkulation nach. Zur Vorbereitung wird im Vorfeld eine den SuS nicht bekannt Kalk ausgearbeitet und die jeweiligen Formeln auf ein Zettel geschrieben, welcher dann in einen Umschlag mit der dazugehörigen Feldangabe gesteckt wird.
Wichtig bei der Auswahl ist natürlich eine Kalkulation mit verschiedenen Zellbezügen aber einfachem und realitätsnahem Thema – z.B. Einkaufs- oder Preisliste für eine Klassenfeier oder ein Stundenzettel für seine Arbeit.
Ich bediene mich hier letzterem Beispiel. Ausgelegt ist es für einen großen Klassenraum mit vielen Schülern.
Das könnte ca. so aussehen
In Formeln ausgedrückt wäre das z.B.:
(Geeignet wäre hier auch eine Umstellung auf die Z1S1-Bezugsart. Ebenso könnte man dies ausweiten und die Uhrzeiten via Zeitwert- und Zeit-Formel richtig umrechnen. Auf Grund der Einfachheit und Umsetzung nehme ich aber die Standarteinstellungen. )
Ein Zettel für das Feld XXX könnte also folgendermaßen aussehen
Umschlag: Für E9 Zettel: Formel: =D9*$F$2
Umschlag: Für D19 Zettel: Kopiere den Inhalt aus D12
Umschlag: Für G5 Zettel: Formel: =D14+D24
Gleich bleibende Werte können entweder vorgegeben sein, oder je nach Klassengröße auch verteilt werden
Natürlich kann hier der Schwierigkeitsgrad sehr variieren in dem man entweder alles vorgibt und wenige Bezüge aufschreibt. Man kann es auch schwieriger gestalten, wenn man z.B. ein Feld in ein anderes Feld kopieren lässt. (siehe im Beispiel D9 im Vergleich zu D14)
Im Unterricht (die vorhergehenden Kenntnisse sind natürlich vorausgesetzt) braucht man zunächst genug Platz um mit Klebeband eine Tabelle inklusive Spalten- und Zeilenbezeichnungen anzukleben. Ideal wäre natürlich ein Zimmer mit großen Kacheln.
Die Größe der ausgearbeiteten Kalkulation muss natürlich dem Klassenzimmer entsprechend angepasst werden.
Der Boden im Klassenzimmer sollte in diesem Fall in etwas so aussehen:
Datei:Zimmertabelle.PNG An allen X steht ein Schüler
Ist das Klassenzimmer aufgeteilt ziehen nun alle SuS einen Umschlag und stellen sich auf das jeweilige Feld. Nun dürfen sie auch die Formeln anschauen und müssen sich die jeweiligen Werte in den dazugehörigen Feldern organisieren, ausrechnen und ggf. weitergeben.
Die ausgerechneten Werte werden aufgeschrieben und der Bezug kurz aufgeschrieben.
Das hieße für E19 (Aufgabe: Kopiere deinen Wert aus E12)
- Ich brauche die Formel aus E12 --> D12*$F$2
- Ich muss diese Formel auf mein Feld umwandeln --> D19*$F$2
- Ich brauche den Wert aus D19 und muss ihn mit F2 multiplizieren --> 4*8€
- Ergebnis = 32€ --> in der Zeigeebene stünde hier „32€“
- Bei Nachfrage muss ich diesen Wert an E24 weitergeben
Wenn die Kalkulation „gelöst“ ist, sollen einige SuS erklären, wie sie ihre Formeln gelöst haben (gerade bei den anspruchsvolleren Formeln). Als Auflösung wird die aufgelöste Kalkulation projiziert und mit der lebendigen verglichen.
"Trockenschwimmen"
[Bearbeiten]Bei dieser Aufgabe bekommen die SuS eine vorgefertigte Tabellenkalkulation ausgedruckt. Allerdings werden einige Angaben leer gelassen. Diese sollen die SuS dann durch nachdenken, Anwendung und vor allem verknüpfen des gelernten Wissens ausfüllen. Diese Aufgabe lässt sich sehr gut in verschiedene Schwierigkeitsstufen aufteilen.
Variante 1)
Die SuS bekommen nur die Zeigeebene ohne Formeln. Da man ohne Formeln nur schwer erraten kann, was dahinter steckt, müssen die SuS knobeln und überlegen was die Formel der jeweiligen Felder sein könnte. Dadurch lassen sich aber nur leichtere Kalkulationen wie Preislisten erarbeiten und schwierigere Bezüge würden nur mit sehr viel Glück gelöst werden.
Variante2)
Die SuS bekommen alle Ebenen ausgehändigt. Nun können komplexere Sachinhalte und Bezüge dargestellt werden. Die Schwierigkeit sollte vor allem auf der Vernetzung und Zusammengehörigkeit der Ebenen liegen.
Problemlösen mit der Tabellenkalkulation
[Bearbeiten]Holzhammermethode
[Bearbeiten]Unter der Brute-Force-Methode (von eng. rohe Gewalt) oder auch "Holzhammermethode", versteht man das konsequente Ausrechnen aller Werte zu einer bestimmten Fragestellung. Diese Methode eignet sich vor allem für die Erzeugung übersichtlicher Datenmengen aus deren Bezugsgrößen. Exemplarisch lassen sich hier Aufgaben zur Berechnung des maximalen Flächeninhaltes einer geometrischen Fläche nennen. Mit Excel steht ein mächtiges Werkzeug zur Verfügung, mit dessen Hilfe man in kurzer Zeit alle berechenbaren Ergebnisse zur Aufgabenstelllung in Tabellenform übersichtlich und geordnet darstellen kann. Die Effektivität der Holzhammermethode nimmt mit der Zahl der zu berücksichtigenden Fälle ab.
Beispiel 1
[Bearbeiten]
Bauer Heinz hat 400 Meter Zaun gekauft und will damit einen Acker umzäunen auf dem er Christbäume anpflanzt, die er auf dem Heidelberger Weihnachtsmarkt in 5 Jahren verkaufen möchte. Natürlich möchte Bauer Heinz so viel Weihnachtsbäume wie möglich auf seinem Acker anpflanzen, um einen hohen Gewinn zu erwirtschaften. Wie groß muss er Länge und Breite des eingezäunten Geländes wählen, damit der Acker einen möglichst großen Flächeninhalt hat?
Der Umfang U des Rechteckes ist durch die Zaunlänge vorgegeben:
U = 2 * Länge + 2 * Breite = 400
Es gibt nun unendlich viele Möglichkeiten, 400 Meter Zaun in 2 * Länge und 2 * Breite aufzuteilen. Untersuche, ob es auch eine Aufteilung gibt, bei der die Fläche
F = Länge * Breite
des Rechteckes möglichst groß ist.
Ziel bei dieser Aufgabe ist es, die optimale Aufteilung zu finden, bei der der Flächeninhalt die maximale Größe erreicht. Dabei wird wie folgt vorgegangen:
Schritt 1:
Zunächst wird eine Tabelle erstellt, mit je einer Spalte für die Länge, die Breite und den Flächeninhalt des Ackers. Zur besseren Übersicht wird noch in eine Zelle der Gesamtumfang von 400m eingetragen.
Schritt 2:
Dann werden für Länge und Breite die Werte eingefügt. Dabei wird in 10er Schritten vorgegangen. Um jede mögliche Aufteilung abzudecken, beginnt man bei der Länge mit 10m und bei der Breite mit 390m (da der Gesamtumfang 400m beträgt). In den darauffolgenden Zeilen werden bei der Länge pro Zeile 10 hinzugefügt und bei der Breite 10m abgezogen. Dies geschieht am besten mit der Funktion "Auto-Ausfüllen".
Schritt 3:
In die erste Zelle der Spalte des Flächeninhalts wird die Formel zur Berechnung des selbigen eingetragen. Die Spalte wird wiederum mit "Auto-Ausfüllen" vervollständigt.
Formelansicht (über Tastenkombination Strg+# darstellbar):
Schritt 4:
Nun lässt sich aus der Tabelle ablesen, bei welchem Längen-Breiten-Verhältnis der Flächeninhalt sein Maximum erreicht. Aus dem Ergebniss wird außerdem ersichtlich, dass der Flächeninhalt dann am größten ist, wenn die Werte von Länge und Breite identisch sind, also ein Quadrat bilden.
Beispiel 2
[Bearbeiten]Der Spielehersteller EA (Electronic Arts) beabsichtigt den neuen Egoshooter Half Life 3 zu veröffentlichen. Das Release des Spiels ist mit 50€ veranschlagt. Beruhend auf den Verkaufszahlen von Half Life 1 und 2 wird mit einer Verkaufszahl von 5 Millionen Exemplaren gerechnet. Nach einer Internetumfrage würde das Spiel je Preissenkung um 0,50€ von 100000 Gamern mehr gekauft werden. Berücksichtigt man diese Voraussetzungen stellt sich die Frage bei welchem Verkaufspreis pro Spiel das Unternehmen den maximalen Umsatz erzielt?
Die erste Grafik des Umsatzes bezieht sich auf alle Werte der Preissenkung von 50€ bis 1€ mit ein. Während sich die zweite Grafik speziell auf die Werte um das Maximum bezieht.
Beispiel 3
[Bearbeiten]Folgende Aufgabe soll die Grenzen der Holzhammermethode aufzeigen:
Ein Betrieb kauft Milch ein und stellt daraus Butter her, die er wiederum verkauft. Es werden 2 Sorten Butter hergestellt, eine mit Kräutern und eine ohne. Die Butter ohne Kräuter wird zu 0,70 Euro pro 250 Gramm verkauft, die mit Kräutern zu 0,90 Euro pro 250 Gramm. Bei beiden Buttersorten erzielt der Betrieb einen Gewinn von 0,10 Euro pro 250 Gramm. Es werden pro Woche von jeder Butter 500 Päckchen a 250 Gramm verkauft. Der Betrieb will den Preis für die Butter mit Kräutern auf 1,00 Euro erhöhen. Der Betrieb rechnet damit, dass die Kunden weniger von der Butter mit Kräutern kaufen werden, dafür aber mehr von der ohne Kräuter.
a) Wie hoch sind die Gesamteinnahmen aus den beiden Buttersorten vor der Preiserhöhung?
b) Wie hoch ist der Gewinn mit den alten Preisen?
c) Wieviel Päckchen (250 Gramm) von der Butter mit Kräutern und der Butter ohne Kräuter müssen mit den neuen Preisen verkauft werden, damit die Gesamteinnahmen gleich bleiben.
Zunächst wird wegen der Übersicht eine Tabelle erstellt, in die die Ausgangswerte der Aufgabe eingetragen werden.
Um nun den richtigen Wert zu finden, müssen verschiedene Tabellen erstellt werden. Da in der Aufgabenstellung beschrieben wird, dass die eine Butter weniger, die andere mehr verkauft wird, es hierfür aber sehr viele Kombinationen gibt, müssen auch sehr viele Tabellen erstellt werden. Jede Tabelle muss folgendermaßen aufgebaut sein: Je eine Spalte für die Stückzahl der Butter ohne Kräuter, eine für die Stückzahl der Butter mit Kräuter und eine Spalte für den Gesamtgewinn. In der Spalte für die Butter ohne Kräuter bleibt der Wert innerhalb der Tabelle immer gleich, wird aber in der nächsten Tabelle um eins erhöht (501,502,...). In der Spalte für die Butter mit Kräutern werden alle Werte von 1 bis 500 angegeben. Dies bleibt auch in den anderen Tabellen erhalten. Die Spalte für den Gesamtgewinn enthält die Werte, die sich aus der Anzahl der Päckchen Butter ohne Kräuter multipliziert mit dem Preis eines einzelnen Päckchens addiert mit der Anzahl der Päckchen Butter mit Kräuter multipliziert mit dem NEUEN Preis für ein Päckchen ergibt (siehe Formelansicht unten).
Am Ende hätte man eine Unzahl dieser Tabellen, aus denen man den gesuchten Wert herraussuchen müsste. Dies wäre ebenso unübersichtlich wie aufwendig!
Formelansicht:
Iteratives Hochrechnen
[Bearbeiten]Im Allgemeinen versteht man unter Iteration die wiederholte Anwendung eines Algorithmus oder eines Programmstücks. Dabei bezieht sich im Normalfall der folgende Iterationsschritt auf das Ergebnis des vorherigen Iterationsschrittes. Eine iterative Berechnung kann beendet werden, indem man nach einer vorgegebenen Anzahl von Iterationsschritten die Durchführung beendet oder indem man eine Abbruch-Bedingung eintreten lässt. Im Mathematikunterricht sieht das so aus, dass man sich bei einer iterativen Lösungsstrategie schrittweise in kleinen Intervallen dem gesuchten Wert nähert, bis dieser erreicht ist.
Beispielaufgaben hierzu wären z.B. folgende:
modulares Arbeiten
[Bearbeiten]Datenstrukturen
[Bearbeiten]Im folgenden werden zu den verschiedenen Grund-Datenstrukturen, Vorschläge zu deren Einführung im Unterricht mit Hilfe der Tabellenkalkulation gegeben.
Stapelspeicher
[Bearbeiten]Der Stapelspeicher oder auch Kellerspeicher genannte Datenstruktur ist eine in der Informatik sehr oft eingesetzte Datenstruktur. In der Theorie kann der Stapelspeicher eine beliebige Menge von Objekten aufnehmen, in der Praxis ist diese Menge jedoch beschränkt. Der Stapelspeicher arbeitet nach dem Last-In-First-Out-Prinzip, also Elemente werden übereinander im Stapel gespeichert und in umgekehrter Reihenfolge vom Stapel genommen.
Ein geeigneter Unterrichtsentwurf zum Thema Stapelschpeicher in Verbindung mit der Visualisierung in Tabellenkalkulationssoftware würde wie folgt ablaufen:
- Erklärung des Stapelspeichers
- Beispiele für Stapelspeicher (Keller, gestapelete Kartons)
- Erwerb von Kenntnissen im Bereich Makros und Buttons
- Erstellen der Tabellenkalkulation mit einer geeigneter Oberfläche zur Visualisierung
- Erstellen von geeigneten Makros, die die Operationen des Stapelspeichers ausführen
- Aufgabenstellung zur Vertiefung (z.B. Türme von Hanoi)
Der Zeitaufwand für diesen Unterrichtsgestaltung ist je nach Kenntnisstand mit der Tabellenkalkulationssoftware mit 3 bis 4 Schulstunden zu rechnen. Für eine weiterführende und vertiefende Aufgabe ist mit bis zu zwei weiteren Schulstunden zu rechnen.
Ein Stapelspeicher hat einen Speicherbereich, in dem die Elemente abgelegt werden können und verfügt über 3 Operationen:
- push – legt Objekt auf den Stapel
- peek – liefert das oberste Objekt des Stapels
- pop – liefert & entfernt das oberste Objekt des Stapels
Der Stapelspeicher ist auch sehr gut an der Tafel skizzierbar.
Der Stapelspeicher kann mithilfe von einer Tabellenkalkulationssoftware sehr gut visualisiert werden. Der Speicherbereich kann durch eine Spalte dargestellt werden, die ebenso in der Theorie unendlich viele, in der Praxis jedoch beschränkt viele Zellen aufnehmen kann. Für die Nutzung der Operatoren werden zusätzliche Kenntnisse der Tabellenkalkulationssoftware gefordert. Hierzu müssen Kenntnisse zum Einfügen von Buttons in Tabellenblättern und das Erstellen von Makros erworben werden.
Es muss den Schülern beigebracht werden, dass ein Makro eine Speicherung von Nutzeraktionen ist und diese auf Aufruf erneut ausgeführt werden.Detaillierte Kenntnisse von Makros in Form von Programmcode ist bei einfachen Beispielen nicht erforderlich, könnte aber bei weiterführenden Aufgaben von Nutzen sein. In Excel 2007 können Makrofunktionen unter dem Reiter Ansicht oder dem Reiter Entwicklertools genutzt werden. In Open Office ist der Zugriff über den Menüpunkt Extras - Makros möglich.
Ein gutes Beispiel zum Thema Makros ist das Kopieren von Inhalten einer Spalte in eine Zeile, dieses Makro kann in unterschiedlichsten Tabellenblättern zum Einsatz kommen. Das Beispiel wird heir in Excel gezeigt, kann jedoch auch mit einer anderen Tabellenkalkulationssoftware realisiert werden.
Im folgenden Schritt soll mit den Schülern eine geeignete Oberfläche für den Stapelspeicher in der Tabellenkalkulation aufgebaut werden. Dazu sollte die Operationen des Stapelspeichers mit einem Button und entsprechendem Ausgabe bzw. Eingabezelle versehen werden. Für den Speicher des Stapels eignet sich eine Spalte. Der Speicher sollte sinnvoll begrenzt werden, um die in der Praxis vorhandene beschränkte Objektmenge des Stapels zu zeigen. Ein-, Ausgabe- und Speicherzellen sollten mit einem Rahmen versehen werden.
Im nächsten Schritt müssen die Operationen mit Makros entwickelt werden:
- push: Alle außer die letzte Zeile des Stapels werden markiert und kopiert (dies beeinhaltet auch leere Zeilen). Die zweite Zeile des Stapels wir markiert und hier wird der vorherige Stapel eingefügt. Der letzte Wert des Stapels wird überschrieben und der Wert geht verloren. Nun wird der Wert von der Eingabespalte kopiert und in die oberste Zelle des Stapels eingefügt.
- peek: Die oberste Zelle des Stapels wird markiert, kopiert und zum Schluss in die Ausgabespalte eingefügt.
- pop: Die oberste Zelle des Stapels wird markiert, kopiert und in die Ausgabespalte eingefügt. Der Bereich zweite Zelle des Stapels bis zur letzten Zelle wird markiert und kopiert. Anschließend wird die Kopie in die oberste Zelle des Stapels eingefügt und die letzte Zeile des Stapels wird gelöscht.
Der erarbeitete Stapelspeicher kann nun im vollen Umfang genutzt werden und zeigt sehr anschaulich den aktuellen Stapel.
Eine Excel 2007 Vorlage zum Stapelspeicher finden Sie unter dem folgenden Link: Stapelspeicher (von Sebastian Bellm).
HINWEIS: Excel 2007 deaktiviert aus Sicherheitsgründen automatisch Makros. Dies wird direkt angezeigt und kann über die Optionen aktiviert werden.
Ringpuffer
[Bearbeiten]Der Ringpuffer eine der eher seltener auftauchenden Datenstrukturen, trägt allerdings stark zum Verständnis und zur Vertiefung von Arrays und Warteschlangen, sowie zum Erwerb von grundlegendem Verständnis für Pointer bei.
Die genannten Themen bilden die Basis für diese Einheit. Listen sollten in jedem Fall erst zu einem späteren Zeitpunkt eingeführt werden, da der Nutzen des Ringpuffers im Vergleich nur gering ausfällt, und die Motivation für dieses Thema rasch verfliegen lässt. (Die Liste ist ohnehin die erste komplexere Datenstruktur, und sollte möglichst erst in der Oberstufe angesetzt sein.)
Zu Beginn sollten die Schüler das Array mit Excel wiederholen, in dem sie selbst eines "konstruieren": Es sollte einen Zeiger geben, und ein Feld das den Inhalt des Feldes ausgibt, auf welches der Zeiger zeigt (siehe SVERWEIS) Sofern die Schüler schon erfahrener im Umgang mit Excel ist, sollte zusätzlich ein Feld zur Eingabe vorhanden sein. Hierzu wird jedes speicherfeld des Arrays mit einer Abfrage ausgestattet, ob ein "Optionsfeld" 1, oder 0 ist. Bei 0, soll einfach der bisherige Wert übernommen werden, bei 1, sofern der Zeiger auf das Feld zeigt, der aus dem Eingabe Feld. Dieser Teil der Aufgabe sollte wiederholend, zusammen mit den Schülern erarbeitet werden. Am Ende dieses Abschnitts befindet sich ein Link zu den fertigen Beispielen.
Bei der Einführung von Warteschlangen hat man bereits schön visualisiert, dass der Aufwand alle Elemente im Array um eine Stelle weiter zu schieben relativ groß ist. Dies sollte hier unbedingt ein weiteres mal getan werden, damit die Schüler sich dem Thema vertrauter fühlen. Hierzu wird den Schülern angedeutet, dass man sich den Wert aus dem Ausgabefeld nun "merkt", oder verwendet bzw., dass dieser nun nicht weiter relevant ist.
Nun hängt es davon ab ob man den Push-Befehl weiter implementiert hat, ist dies der Fall, schreiben wir in das Eingabefeld " =(Feld unter dem 1. Feld)". Setzt man nun die "Push"-Option auf 1, wird der Wert aus Feld 2, in Feld 1 kopiert. (Den Wert zu verschieben wäre zusätzlicher Aufwand, was den Schülern klar werden sollte, wenn am Ende der letzte Wert immer noch im Array steht.) Ohne diese Implementierung kopiert! man die Werte immer von Hand. Dies mag einem sogar als weitaus visualisierender vorkommen, jedoch sollte man bedenken, dass beim Kopieren von Hand der Wert in den Zwischenspeicher abgelegt werden, wohingegen ein Array ohne diesen zusätzlichen Speicherbedarf auskommt.
Anregung: Arbeitet man auf Windows XP oder älter, steht als Zugriff auf diesen Zwischenspeicher das Clipboard zur verfügung. (Zugriff über Ausführen oder cmd: "clipbrd", oder direkt im WINDOWS\system32\-Ordner.) Es ist in diesem Moment nicht wichtig ob die Schüler den eigentlichen "Vorteil" des direkt-kopierens kennen. Wenn man also schon von hand kopiert, lohnt es sicher, einen Zwischenspeicher auf diese Art und Weise vorzustellen. (Für aktuellere Betriebssysteme gibt es ausreichend Tools um dies vorzuführen.)
Nachdem den Schülern (erneut) klar gemacht wurde, dass den Speicher hier und her zu schieben ziemlich aufwändig ist, sollten diese selbst auf die Idee kommen, lieber den "Auslese Zeiger" dynamisch zu gestalten. Ist diese Idee gekommen, sollte es keine allzu große Schwierigkeit darstellen, das nun umzusetzen. Je nachdem wie der Kenntnisstand der Schüler ist, kann man das beliebig weit automatisieren, so dass beim Pushen und Poppen die Zeiger automatisch inkrementiert werden, im Kreis laufen und das "Push-Option auf 1, und wieder auf 0 setzen" über ein Makro beschleunigt wird.
Beispiele zur Anwendung von Ringpuffern sind unter anderem die Flugschreiber, die nur die Informationen kurz vor einem Absturz zu speichern brauchen, und den Speicher daher zyklisch überschreiben. Viele Programme merken sich die letzten x Bearbeitungs-Schritte. Auch dies ist per Ringpuffer sehr gut realisierbar. Wenn man die Menge an ankommender Information gut voraussehen kann, bzw. diese geregelt sind, ist der Ringpuffer natürlich auch wunderbar als Warteschlange einsetzbar, da alle Aktionen in linearer Zeit ablaufen.
An Zeitaufwand sollte je nach Kenntnisstand mit Excel mit mindestens 4 bis 6 Schulstunden, für die Einführung in den Ringpuffer bis zur Fertigstellung des Programms gerechnet werden. Es tut den Schülern unter Umständen auch ganz gut, wenn sie für jede Stunde eine Vorlage haben an der weitergearbeitet werden kann, falls jemand überhaupt nicht mit der Aufgabe zurecht kam.
Die Vorlagen zum Array, und zum fertigen Puffer finden sie unter dem folgenden Link: Ringpuffer-Vorlagen (von Julien Meisenzahl)
HINWEIS: Excel arbeitet die Neuberechnungen von links oben, Zeile für Zeile ab. Das heißt, wenn eine Zelle, darauf angewiesen ist, dass sich eine andere Zelle vor ihr ändert, dann muss dies bei der gestaltung der Tabelle beachtet werden!
Algorithmen
[Bearbeiten]Im folgenden werden zu verschiedenen Algorithmen, Vorschläge zu deren Einführung im Unterricht mit Hilfe der Tabellenkalkulation gegeben.
Suchverfahren
[Bearbeiten]Einleitung und die sequenzielle Suche
[Bearbeiten]
Der Sinn der Sicherung von Daten ist es, schnell wieder darauf zugreifen zu können. Deswegen ist es sinnvoll, nach Elementen mit bestimmten Kriterien zu filtern beziehungsweise zu suchen.
Die Suche ist eine grundlegende Operation von Computersystemen. Viele Probleme können mithilfe von „Suchen“ gelöst beziehungsweise erleichtert werden.
Die Suche eignet sich besonders gut für den ITG als auch den Informatikunterricht, da sie einen guten Einstieg in den Themenbereich „Algorithmus“ durch einfache Operationen bietet, als auch sehr viele anschauliche Aspekte besitzt. So kann man den Schülern eine Packung mit farblich verschiedenen verpackten Bonbons geben, die Schüler sollen dann bestimmte „Farb-Bonbons“ suchen und ihre Vorgehensweise erklären und aufschreiben. Danach erarbeitet man diese Vorgehensweise aus der Sicht eines Computers auf.
Man hat somit schon den ersten und einfachsten Suchalgorithmus gefunden, die „sequenzielle Suche“. Man kann daraufhin andere effizientere Suchalgorithmen mit den Schülern diskutieren, z.B. die „Binäre Suche“, indem man die Bonbons erst der Farbe nach sortiert.
Ein Vorteil der Suche ist, dass der Großteil des Themas sowohl am Computer als auch an der Tafel ohne Probleme darstellbar ist.
Nachdem die Schüler das Prinzip und die Grundlagen der Suche verstanden haben, kann man mit der Implementierung des Algorithmus in die Tabellenkalkulation beginnen.
Ein guter Unterrichtsentwurf zum Thema „Suchalgorithmus mithilfe Tabellenkalkulation“ wäre:
- Motivierender Einstieg (z.B. verschieden Bonbons suchen)
- Suchalgorithmus in eigenen Worten und in Programmiersprache aufschreiben
- Andere Suchalgorithmen besprechen
- Wiederholung von Zellbezügen, Iteration, WENN- und UND-Befehlen
- Vorstellen einer Beispielsuche in der Tabellenkalkulation
- Schüler implementieren die Suche in der Tabellenkalkulation selbst
Man sollte einen Zeitaufwand von etwa 2-3 Schulstunden für den Einstieg einplanen und weitere 2-3 Schulstunden, je nach Vorkenntnissen, für die Implementierung des Suchalgorithmus in die Tabellenkalkulation.
Man kann mit dem Suchalgorithmus auch weitere Elemente wie z.B. Makros und einfache Programmierungen (If-Else, Do-While-Schleife) sehr anschaulich erklären.
Der Zeitaufwand würde sich dabei jedoch auf mindestens 10 Schulstunden erhöhen.
Die Ziele des Suchalgorithmus sind,
- Struktur und Dynamik eines Suchalgorithmus verstanden zu haben
- Verschiedene Suchalgorithmen zu kennen:
- Sequenzielle Suche
- Binäre Suche
- Anwendungsfälle für verschieden Suchalgorithmen zu kennen
- Gemeinsamkeiten und Unterschiede verschiedenen Suchalgorithmen zu kennen
Alle Suchalgorithmen haben gemeinsam, dass sie aus einer Menge von Elementen, die eindeutig durch einen Schlüssel identifiziert sind (z.B. Zahlen und Buchstaben), nach einen bestimmten Schlüssel suchen.
Einer der Unterschiede zwischen der sequenziellen und der Binären Suche ist, dass die Binäre Suche auf einer sortierten Datenstruktur (Array oder einfach verkettete Liste) operiert und die sequenzielle Suche keine Sortierung benötigt, dafür jedoch auch ineffizienter ist. Da die Sortierung unter Umständen den Schülern noch nicht bekannt ist, eignet sich die sequenzielle Suche für die Implementierung eines Suchalgorithmus im Unterricht besser.
Da die zu durchsuchende Menge nicht sortiert ist, muss bei der sequenziellen Suche die komplette zu durchsuchende Menge durchlaufen und jedes Element mit dem Suchschlüssel verglichen werden. Die Suche ist dann beendet, wenn entweder das Element gefunden wurde oder das letzte Element der Menge verglichen wurde. Da es in der Tabellenkalkulation keinen eindeutig bestimmten „Return“-Wert gibt, muss die Suche nicht abgebrochen werden, sobald zum ersten Mal das Suchwort gefunden worden ist.
Es ist wichtig, dass man dies den Schülern klarmacht um Missverständnisse vorzubeugen. Eine Implementierung, bis zum ersten Finden des Suchwortes, ist in Excel auch möglich, aber für einen Einstieg ungeeignet.
Ein Beispiel-Pseudo-Code für solch eine modifizierte sequenzielle Suche wäre:
sequentiel_Search(array,suchwort){
// es soll ein zu durchsuchendes Array und ein Suchwort übergeben werden
n=len(array); // die Variable n enthält die Länge des zu durchsuchenden Arrays
Hilfs_array[n]; // ein temporäres Hilfsarray
flag=0;// eine temporäre Hilfsvariable, die das Hilfsarray durchlaufen wird
for(int i=0; i<n; i=i+1){ // eine Schleife, die das Array von vorne bis hinten durchläuft
if (array[i]==suchwort){ // falls das Wort an der "i-ten" Stelle das Suchwort ist:
Hilfs_array[flag]=i; // schreibe die Stelle des Wortes in das Hilfsarray (i)
// Vorsicht, der Computer zählt von 0-(n-1) !!
flag=flag+1; // erhöhe die Hilfsvariable um 1, damit nicht eine schon
//beschrieben Stelle überschrieben wird
}
}
If (flag==0) {
array[flag]= -1; //falls das Suchwort nicht gefunden wurde, wird in das
//Hilfsarray eine -1 eingetragen, damit jegliche Irrtümer
//ausgeschlossen werden können.
}
return Hilfs_array; //gebe das Hilfsarray, das alle Positionen, in denen das Suchwort
//gefunden wurde, zurück
}
Je nach Wissensstand kann man die Komplexität des Algorithmus anhand des Beispielcodes errechnen oder durch Betrachten der Vorgehensweise des Algorithmus sehen. Da das Array jedes Mal von vorne bis hinten durchlaufen wird, ist die Komplexität immer n, wobei n die Länge des Arrays ist.
Auch hier sollte man herausstellen, dass das nur bei dem modifizierten Algorithmus der Fall ist. Bei der Standard-Sequenziellen-Suche beträgt die Komplexität unter Annahme, dass alle n Elemente unterschiedlich sind:
[1]
Falls alle Elemente gleich wahrscheinlich sind gilt außerdem:
→
Implementierung der sequenziellen Suche in die Tabellenkalkulation
[Bearbeiten]
Im Folgenden wird die Implementierung des Suchalgorithmus in die Tabellenkalkulation behandelt. Um das Prinzip des Algorithmus näher zu bringen, wird der Einfachheit wegen nur die sequenzielle Suche auf einem unsortierten Array der Größe 10 in Excel bearbeitet.
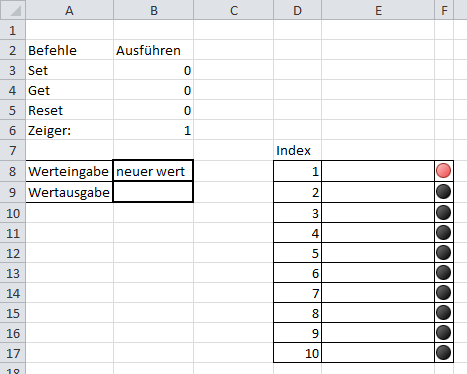
Die Excel Oberfläche sollte beispielsweise wie folgt aussehen:

Um den Beispielcode wie oben zu implementieren, sind eine Schleife, Vergleichsoperationen und Zählvariablen nötig. Excel besitzt keine reine „Return“-Operation, deswegen wird dies durch rein visuelle Aspekte ersetzt.
Um die Schleife zu simulieren, benötigt man eine Iteration. Diese ist in Excel standardmäßig deaktiviert. Um sie zu aktivieren müssen Sie:
Auf den Reiter: Datei → Optionen → Formeln → und ein Kontrollhäkchen bei „Iterative Berechnung aktivieren“ setzen. Es sollten nun die Einstellungen, wie sie unten im Bild zu sehen sind, übernommen werden.
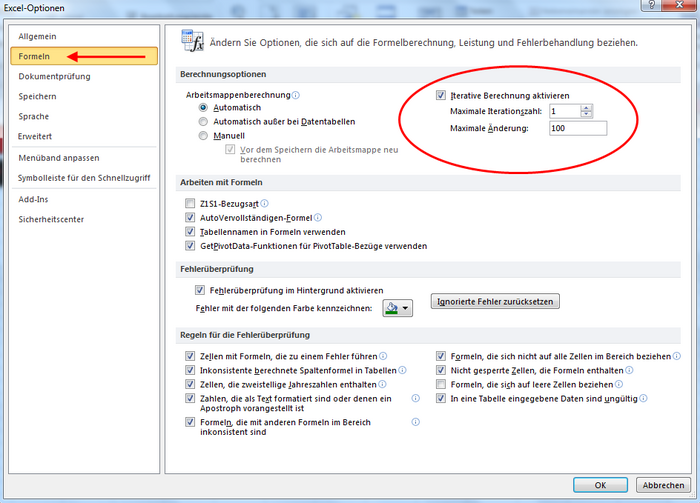
Wenn man sich den Beispielcode anschaut, werden der Funktion ein zu durchsuchendes Array und ein Suchwort übergeben. Das zu durchsuchende Array ist in diesem Fall das blau markierte Feld (Abb. 1.3). Hier können die zu durchsuchenden Elemente eingetragen werden, wichtig hierbei ist, dass die zu durchsuchenden Schlüssel eingetragen werden!
Über den Elementen ist ihre Position in dem Array (0-9) angegeben.

Das Suchwort wird in dem links oben stehenden( Abb.1.1) Feld eingetragen (Abb 1.3).
Im rechten oberen Bereich (Abb.1.1.) ist ein Feld mit einer Zählvariablen „Count“, die angibt welches Feld momentan überprüft wird und einer Variable „Anzahl“, die die Menge von gefundenen Elementen angibt. Falls die „Count“-Variable auf „-1“ steht, ist die Suche gestoppt (Abb.1.5.).
Der Befehl des Count Befehls lautet:
=WENN(UND(START=1;COUNT<9);COUNT+1;WENN(START=0;-1;COUNT))
Die Zelle prüft zuerst, ob der Algorithmus gestartet ist und ob ihr eigener Zahlenwert kleiner als 9 ist. Ist dies der Fall, addiert sie ihren eigenen Zahlenwert um eins. Falls der Startwert jedoch 0 ist, der Suchalgorithmus also gestoppt ist, wird ihr Zahlenwert auf -1 (siehe Abb.1.5) gesetzt. Ist der Zahlenwert bereits 9, wird dieser beibehalten.
Hier wird vor allem ersichtlich, dass Iteration genutzt wird, da sich die Zelle selbst wieder aufruft.
Bevor das Array durchsucht wird, muss der Algorithmus erst aktiviert werden. Dafür befindet sich neben dem Sucharray ein farbiges Feld, das dies anzeigt. Ist das Feld rot (Abb.1.6), wurde der Algorithmus gestoppt, ist es allerdings grün, so ist der Algorithmus betriebsbereit. Dies kann durch manuelles Eintragen von „0“ oder „1“ in das obere Feld erreicht werden. Trägt man die „0“ ein, wird der Algorithmus automatisch gestoppt, auch wenn die Suche noch nicht beendet wurde. Trägt man eine „1“ ein (Abb1.7), ist der Algorithmus wieder aktiviert, allerdings muss die Suche wieder von Anfang an durchgeführt werden.
Nachdem die Suche gestartet wurde, ändert sich auch die Oberfläche des Sucharrays. Die zuvor blauen Felder (Abb.1.3), wurden bis auf ein rosa Feld farblos. Dieses rosa Feld signalisiert, welches der Elemente gerade durchsucht wird (Abb1.8). Um das nächste Feld zu überprüfen, muss Excel aktualisiert werden, dies passiert durch einen Druck auf die F9-Taste.

Die Überprüfung erfolgt durch den Befehl:
=WENN(UND(START=1;COUNT>=Position);WENN(Array(COUNT)==Suchwort;1;" ");" ")
Hier wird die Schleife aus dem Beispielcode durchgeführt. Es wird zuerst geprüft, ob der Algorithmus gestartet und die Position des zu prüfenden Elements erreicht wurde (in der Formel wird ein „≥“ anstatt einem „=“ verwendet. Da dies sicher stellt, dass ein gefundenes Element bis zum Ende der Iteration, also Count = 9, gekennzeichnet bleibt und nicht wieder gelöscht wird). Ist der Algorithmus gestartet, so wird das durch „Count“ bestimmte Element mit dem Suchwort verglichen. Stimmt es überein, färbt sich das Feld um das Suchwort gelb und es wird darunter eine „1“ geschrieben. Die „Anzahl“ erhöht sich daraufhin ebenfalls um eins. Außerdem wird in die entsprechende „Adresse“-Zeile (Abb.1.8) die Adresse des gefundenen Elements eingetragen. Dies geschieht durch Excels =ADRESSE-Befehl.

Ist die Suche bis zum Ende durchlaufen, bleiben gefundene Elemente gelb markiert und die restlichen Elemente werden wieder blau markiert (Abb.1.10). Nun kann man durch das Eintragen einer „0“ in das Start-Feld, die Suche beenden.

Fortgeschrittene Implementierung der Suche
[Bearbeiten]
Wie schon angesprochen, eignen sich Suchalgorithmen bestens, um Makros und einfache Programmier-Begriffe in der Schule einzuführen. Dies geschieht anhand eines anschaulichen Beispiels, nämlich der „Suche“: Die Schüler haben diese bereits durchdacht und die Vorgehensweise des Algorithmus verstanden.
Da ständiges Drücken der F9-Taste oder auch das manuelle Eintragen der „0“ oder „1“, um den Algorithmus zu starten bzw. beenden, lästig sein kann, kann dies unter Excel 2010 sehr einfach durch Makros behoben werden. Makros speichern einen „vorgeführten“ oder programmierten Arbeitsauftrag und können diesen jederzeit ausführen. Da dies zu Sicherheitslücken führen kann, sind diese standardmäßig in Excel 2010 deaktiviert. Sobald man eine Arbeitsmappe öffnet, die Makros enthält, wird man gefragt, ob man den Inhalt (Makros) aktivieren möchte (Abb2.1).

Möchte man trotzdem mit Makros arbeiten, findet man das Makro-Menü in Excel durch Klicken auf den Reiter „Ansicht“ und Auswählen des Menüpunktes „Makros“ (Abb.2.2).

Nun gibt es zwei Möglichkeiten ein Makro zu erstellen. Man kann ein Makro „aufzeichnen“ (Abb.2.2 mittlere Option) oder in VBA (Visuell Basic for Applications) programmieren. Letzteres ist für fortgeschrittene Schüler geeignet.
Will man ein Makro aufzeichnen, klickt man auf das entsprechende Symbol (Abb.2.2). Nun wird man aufgefordert, dem Makro einen Namen zu geben und kann auch gegebenenfalls eine Tastenkombination, den Speicherort des Makros und eine Beschreibung festlegen. Hat man dies getan, bestätigt man diesen Vorgang durch Klicken auf „OK“. Das Menü verschwindet und man kann in seiner Arbeitsmappe Veränderungen durchführen, die das Makro später „nachmachen“ wird. Beispielsweise kann man ein Reset-Makro in die Suche implementieren, das das Start Feld zuerst auf „0“ setzt und danach wieder auf „1“, so kann man ganz einfach eine neue Suche starten.
Hat man dies getan klickt man wieder auf „Makros“ (Abb.2.2), der Menüpunkt „ Makros aufzeichn.“ Sollte durch „Aufzeichnung beenden“ (Abb.2.3) ersetzt sein.
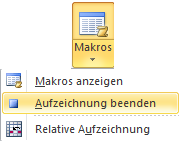
Wenn alle Änderungen, die durchgeführt werden sollten, gemacht sind, klickt man auf „Aufzeichnung beenden“. Dies speichert die durchgeführten Veränderungen, führt sie jedoch nicht aus. Es sollte nun der Menüpunkt „Makros aufzeichn.“ wieder verfügbar sein.
Nun muss man das Makro nur noch durch ein geeignetes Mittel auswählbar machen, es eignen sich, unter anderen, einfache Buttons. Hier kann man seiner Fantasie freien Lauf lassen, wie der Button aussehen soll, beispielsweise findet man eine Vorlage für einen Button unter: Einfügen→Formen (Abb.2.4)

Hat man einen Button erstellt, kann man mit einem Rechtsklick auf den Button die Option „Makro zuweisen…“ auswählen (Abb.2.5):

Man wählt aus der erschienenen Liste nun das entsprechende vorher erstellte Makro aus und bestätigt dies mit „OK“. Nun ist der Button aktiviert und jedes Mal, wenn dieser gedrückt wird, führt er die entsprechende Operation aus. Macht man während des Erstellens eines Makros einen Fehler oder benötigt ein Makro nicht mehr, kann man im Makro-Menü (Abb.2.2 oder Druck der Tastenkombination ALT+F8), das entsprechende Makro auswählen und es löschen.
Man kann diesen Vorgang als Lehrer zur Einführung in das Thema „Makros“ sehr gut nutzen und lässt beispielsweise danach die Schüler selbst drei Buttons, einen der eine Iteration durchführt, einen „Start“- und einen „Stopp“ – Button erstellen, die alle durch Makros die entsprechenden Operation durchführen.
Da das Feld zum Starten des Algorithmus nun nicht mehr von Hand mit „0“ oder „1“ ausgefüllt werden muss, sondern durch die Buttons gesteuert wird, steht es einem frei dieses nach Belieben zu gestalten. Das könnte dann wie folgt aussehen (Abb.2.6):

Möchte man nun die Makros programmieren um z.B. Schleifen oder Zusatzoptionen festzulegen, geht das wie folgt: Wie in beim Aufzeichnen der Makros wählt man wieder unter Ansicht→Makros aus. Doch dieses Mal wählt man nicht die Option „Makros aufzeichn.“ sondern „Makros anzeigen“ oder durch die Tastenkombination: ALT+F8. Hier kann man die Makros verwalten, neue erstellen, indem man einen noch nicht vergebenen Namen unter Makroname eintippt, und Bearbeiten. Möchte man nun die gleichen Buttons wie vorhin jetzt durch Programmieren erstellen, erzeugt man dafür ein neues Makro. Eine neue VBA Oberfläche erscheint in der bereits Sub „Makroname“ und End Sub stehen. Hier können durch Programmierbefehle, die bereitgestellt werden sollten, die einzelnen Buttons nachprogrammiert werden.
Durch das Programmieren und die zahlreichen Befehle werden dem Benutzer viel mehr Möglichkeiten gegeben, Makros zu kreieren. Man kann z.B. einen weiteren Button erstellen, der die Iteration durch einen Knopfdruck bis zum Ende durchführt und damit auch die Suche beendet. Man kann außerdem bestimmen, was passiert, wenn eine falsche Eingabe durch den Benutzer passiert z.B. eine Warnung, falls der Iterations-Button gedrückt wird, obwohl die Suche gestoppt ist.
Ein Beispielscode in VBA für einen Button der bis zum Ende iteriert und bei falschen Aufrufen des Makros eine Warnung ausgibt, kann wie folgt aussehen:
Public blnFlag As Boolean 'eine öffentliche Variable, die angibt ob die Suche beendet wurde
Sub Ende1() 'Makroname
strText = " Uebereinstimmungen gefunden." ' Text zur späteren Ausgabe
strText1 = " Uebereinstimmung gefunden." ' Text zur späteren Ausgabe
Dim i As Integer 'Zählvariable i
i = 0 'setze i = 0
If (Range("C3").Value = "0") Then 'Falls im Start-Feld eine 0 steht dann:
MsgBox "Suche ist gestoppt!", vbCritical + vbOKOnly ' lasse eine Error-Box erscheinen
Else 'andernfalls
Do While (Range("Q1").Value < 9) 'Mache Folgendes, solange Count < 9:
Range("Q1").Select 'einen Iterationsschritt
Calculate 'einen Iterationsschritt
Loop 'Wiederhole -> Schleife
If (Range("Q1").Value = 9 And blnFlag = 0) Then
'Falls Count =9 ist und die Suche zuvor noch nicht beendet wurde (Flag=0)
blnFlag = 1 ' Setze Flag=1 und zeige dadurch, dass die Suche beendet wurde
If (Range("Q2").Value = 1) Then 'Falls es einen Suchtreffer, gab schreibe es in Info-Box
MsgBox ("Fertig! Es wurde " & (Range("Q2").Value) & strText1)
ElseIf (Range("Q2").Value = 0) Then 'Falls es keine Suchtreffer gab
MsgBox "Fertig! Es wurden keine Uebereinstimmungen gefunden."
Else 'falls es mehr als einen Suchtreffer gab
MsgBox ("Fertig! Es wurden " & (Range("Q2").Value) & strText)
End If
ElseIf (Range("Q1").Value = 9) Then ' Falls die Suche zuvor schon beendet wurde:
MsgBox "Suche ist durchlaufen! Bitte starten Sie eine neue Suche!", vbCritical + vbOKOnly
'lasse eine Error-Box erscheinen, die angibt, dass die Suche bereits durchlaufen ist
End If
End If
End Sub
Wenn man nun auf seiner Oberfläche den entsprechend programmierten Knopf auswählt, erhält man, während die Suche gestoppt ist, durch einmaligen Druck des Buttons die Meldung aus „Abb.2.7“ und solange die Suche gestartet ist, durch zweimaliges Drücken die Meldungen „Abb.2.8“.
 |
 |
Der Schwierigkeitsgrad eines solchen Codes geht bei weitem über die Einführung in das Thema „Makros“ hinaus. Man kann es zu einem späteren, fortgeschrittenen Zeitpunkt wieder aufgreifen. Außerdem kann es während der Einführungsphase von der Lehrperson zur Motivation gezeigt werden, was mit Makros leicht möglich ist oder man lässt eine solche Aufgabe von fortgeschrittenen Schülern bearbeiten, die sich von dem Unterrichtsstoff unterfordert fühlen.
Fazit
[Bearbeiten]
Der Suchalgorithmus ist sehr vielseitig und auf verschiedenen Ebenen einsetzbar. Man kann eine Suche mit einfachen WENN- und UND- Befehlen, in der Unterstufe, erstellen aber auch durch kompliziertere Makros, mit fortgeschrittenen Schülern, die gleiche Suche auf einem komplett anderen Weg erhalten (Spiralprinzip). Wenn man nun auch andere Suchalgorithmen betrachtet und implementiert, kann man ein breites Spektrum der Tabellenkalkulation und ITG abdecken und bearbeiten. Das alles findet auf einer sehr anschaulichen und einfachen Basis statt, die sich schon Jugendliche gut vorstellen und nachvollziehen können.
Durch die vielfältigen Möglichkeiten, die der Suchalgorithmus bietet, ist eine präzise Planung zwingend. Damit der zeitliche Rahmen abgeschätzt und eingehalten werden kann und nicht aus Zeitmangel abgebrochen werden muss.
Excel-Files und Anleitung
[Bearbeiten]
Die Such-Excel Files, mit und ohne Makros, findet man hier:
Eine Anleitung zum Arbeiten mit den Suchverfahren in Excel findet man hier:
Quellen und Literaturverzeichnis
[Bearbeiten]- ↑ Pomberger, G. & Dobler,H. (2008). Algorithmen und Datenstrukturen. S.275
- Balzert, H. (2005). Lehrbuch Grundlagen der Informatik. (2., durchgesehene Auflage der deutschen Ausgabe)
- Pomberger, G. & Dobler,H. (2008). Algorithmen und Datenstrukturen. Eine systematische Einführung in die Programmierung.
- Köthe, U. (2012). Vorlesung Algorithmen und Datenstrukturen. http://alda.iwr.uni-heidelberg.de/index.php/Suchen (Stand 09.02.13)
- Bastian. P (2011). Vorlesung Einführung in die Praktische Informatik. http://conan.iwr.uni-heidelberg.de/teaching/info1_ws2011/info1-skript.pdf
Sortierverfahren
[Bearbeiten]Einstieg in das Thema
[Bearbeiten]Das Sortieren von Daten spielt in der Informatik eine wichtige Rolle, denn in fast jedem Softwaresystem sind Sortier- und Suchvorgänge notwendig.[1] Darüber hinaus sind Sortieralgorithmen bestens geeignet, um einen visuellen Einstieg in das Thema Algorithmenentwicklung zu bieten.[2] Ein früher Umgang mit Sortieralgorithmen sollte daher schon in der Schule angestrebt werden. Das Prinzip des Sortierens ist zudem jedem Schüler bekannt, da der Mensch elementare Verfahren nutzt um Dinge zu sortieren. So findet sich schnell ein Einstieg in das Thema „Sortieren“, zum Beispiel indem der Lehrer die Schüler ein Kartenspiel aufsteigend sortieren lässt. Nachdem der Lehrer den Schülern einen Einstieg in das Thema geboten hat, sollten noch einige elementare Dinge zum Thema „Sortieren“ besprochen werden. Erst dann sollte man eine Implementierung in einer Tabellenkalkulation angehen. Ein möglicher Entwurf zur Planung der Unterrichtseinheiten wäre:
- Motivation (z.B. durch das Sortieren eines Kartenspiels)
- Besprechung der Anwendungsbereiche von Sortierverfahren
- Besprechung verschiedener Sortierarten
- Vorstellen des Sortieralgorithmus, der implementiert werden soll
- Wiederholung der Themen „iteratives Hochrechnen“ und „Zellbezüge“
- Implementierung des Sortierverfahrens unter Anleitung
Man sollte hierbei mit einem Zeitaufwand von drei Schulstunden rechnen, bis man mit der Implementierung des Verfahrens beginnen kann. Dies benötigt erneut mindestens drei Schulstunden, wenn man den Schülern bereits eine vorgefertigte Datei zur Vervollständigung anbietet. Den Schülern sollte vermittelt werden, dass es verschiedene Arten von Sortierverfahren gibt:
- Beim Auswahlsortieren wird auf dem zu sortierenden Feld das kleinste Element ermittelt, um es dann an die erste Stelle zu tauschen. Dies wiederholt man induktiv auf dem restlichen Feld, bis die Datenreihe sortiert vorliegt.
- Beim Einfügesortieren geht man davon aus, dass das erste Element bereits korrekt sortiert ist und fügt das nächste Element nun an der richtigen Position ein. Dies wiederholt man ebenfalls bis alle Elemente an der korrekten Stelle einsortiert wurden.
- Das Austauschsortieren hingegen tauscht benachbarte Elemente so lange, bis das gesamte Feld sortiert ist. Ein Paradebeispiel hierfür ist der Algorithmus Bubblesort.[3]
Bubblesort
[Bearbeiten]Bubblesort tauscht benachbarte Elemente so, dass das größte Element im ersten Durchlauf an der letzten Stelle des Feldes landet und somit korrekt sortiert wurde. Dann wiederholt Bubblesort diesen Vorgang für das restliche Feld. Hierbei wandern die großen Elemente relativ schnell nach hinten, kleinere Elemente im hinteren Teil des Feldes jedoch ziemlich langsam an den Anfang des Feldes. Man vergleicht dieses langsame Aufsteigen der kleinen Elemente mit dem Aufsteigen von Luftblasen in einer Wasserflasche – daher auch der Name „Bubblesort“.
Eine mögliche Implementierung in Pseudocode lautet:
bubbleSort(array):
{
for (n=array.size; n>1; n=n-1) {
// durchläuft den Index des letzten unsortierten Elements
for (i=0; i<n-1; i=i+1) {
// durchläuft die Indizes aller Elemente bis zu diesem Element
if (array[i] > array[i+1]) {
// falls Element an i-ter Stelle größer ist als das Element an i+1-ter Stelle
array.swap(i,i+1)
// tausche die Element
}
}
}
}
Den Schülern kann man anhand dieses Beispiels besonders gut das Laufzeitverhalten von Algorithmen erklären, indem man mit ihnen die Anzahl an Vergleichen für ein zu sortierendes Array der Länge n nachvollzieht: So werden im ersten Schleifendurchlauf (n-1) Vergleiche durchgeführt, im zweiten Durchlauf noch (n-2), bis im letzten Durchlauf nur noch einmal verglichen wird.
Insgesamt ergibt dies ++⋯+= ~ Vergleiche. Bubblesort hat somit eine Laufzeitkomplexität . [4]
Die Laufzeitkomplexitäten spielen später eine wichtige Rolle, um verschiedene Algorithmen vergleichen zu können und schnellere Verfahren zu entwickeln.
Implementierung in Excel
[Bearbeiten]Zur Vereinfachung wird im Folgenden davon ausgegangen, dass ein Array mit zehn Elementen vorliegt. Um die beiden for-Schleifen mit einem Tabellenkalkulationsprogramm zu programmieren benötigen wir nun Vorkenntnisse im Bereich der Iteration, da sich Zellen selbst verändern müssen. Um dies zu gewährleisten müssen in Excel 2010 folgende Einstellungen vorgenommen werden: Unter Datei / Optionen / Formeln existiert ein Kontrollhäkchen „Iterative Berechnung aktivieren“. Dieses sollte gesetzt werden und bestenfalls so eingestellt werden:
Die beiden Variablen n und i (vgl. Implementierung) sollten nun nacheinander folgende Werte annehmen:
=,,,…,,,…,,,…,,…,,,
Dies lässt sich mit folgendem Aufbau realisieren:
Falls START auf 0 gesetzt ist, soll nichts geschehen. Im Fall, dass START auf 1 gesetzt ist, sollen n und i die gewünschten Werte annehmen. Für n ergibt sich damit folgende Pseudo-Formel:
=WENN(START=0;9;WENN(n=i-1;WENN(n>1;n-1;n);n))
Diese realisiert das gewünschte Verhalten, da es n zu Beginn auf 9 setzt und immer dann dekrementiert, falls i+1=n gilt. Für i ergibt sich die Formel:
=WENN(START=0;-1;WENN(i=n;0;WENN(n<>1;i+1;i)))
Hierbei wird i zu Beginn auf -1 gesetzt, um den Wert (9,0) erst bei START=1 vorliegen zu haben. Nun wird i solange inkrementiert, bis es n entspricht. In diesem Fall wird i erneut auf 0 gesetzt, während sich n um 1 erniedrigt. Dies geschieht nur so lange bis n den Wert 1 annimmt. Das Durchlaufen der gewünschten Werte wird nun durch die Aktualisierung der Excel-Mappe, durch Drücken der F9-Taste bewerkstelligt. Nun benötigen die Schüler noch den Grundaufbau des Arrays und die Realisierung der eigentlichen Tauschvorgänge, um Bubblesort zu vervollständigen. Sinnvoll ist es nun, anzusprechen, dass „normale“ Tauschvorgänge innerhalb zweier Zellen nur schwer in Excel realisierbar sind.
In Pseudocode ist der Tausch über eine dritte Variable einfach zu implementieren:
int x=3
int y=5
int z=x //Tauschvariable
x=y
y=z
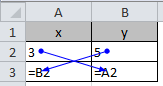
In Excel geht dies nicht, was man anhand folgenden Beispiels leicht rekapitulieren kann:
x ist hier auf 3 gesetzt und y auf 5. z übernimmt den Wert von x. Ändert man diesen nun auf den Wert von y, also auf 5, so ändert sich automatisch auch z, da die Zelle nur eine Referenz auf die Zelle A2 darstellt. Das Problem kann man allerdings sehr leicht umgehen, indem man eine neue Zeile zuhilfe nimmt:
Durch die Verlagerung des Tausches in eine neue Zeile vereinfacht sich das eigentliche Tauschen stark, man benötigt allerdings weiteren Speicherplatz.
Bei Bubblesort benötigen wir solche Tauschvorgänge in jedem Schritt, indem beim Vergleich innerhalb des Arrays der Wert in der linken Zelle größer ist als der Wert in der rechten Zelle. Durch die Iteration durch das gesamte Array, wie in der bereits angesprochenen Iterationsfolge, ergibt sich folgende diagonale Vertauschungsform beim Realisieren von Bubblesort in einer Tabellenkalkulation:
Hierbei visualisieren die roten Zellen die eigentlichen Daten. Das Array darunter soll im ersten Schritt die Daten übernehmen. Danach werden die Vergleichs- und Tauschoperationen ausgeführt, was in den diagonal gestaffelten Zellen geschehen soll. Nach einem Schleifendurchlauf werden nun die teilsortierten Elemente in das unterste Array übernommen. Nun übernimmt das obere Array die Werte aus dem unteren und der gesamte Vorgang wird wiederholt (im Pseudocode des Algorithmus also die innere for-Schleife mit den Vergleichen und Vertauschungen), bis das Array komplett sortiert vorliegt. Hierbei sollten die Schüler besonders den Zusammenhang zwischen den gestaffelten Zellen und den Variablen n und i erkennen.
Eine mögliche Lösungsformel für das erste Zellenpaar lautet unter der Annahme, dass a das bis zu diesem Zeitpunkt teilsortierte Array ist:
=WENN(START=1;WENN(i=0;WENN(a(0)>a(1);a(1);a(0));startarray(0));0)
und
=WENN(START=1;WENN(i=0;WENN(a(0)>a(1);a(0);a(1));startarray(1);0)
Wenn die Schüler die Tauschvorgänge für all diese gestaffelten Zellen implementiert haben, muss lediglich das untere Array das teilsortierte Array übernehmen. Hierbei muss man beachten, dass auf der Diagonalen die neue Sortierung vorliegt und diese nur bis zu einer bestimmten Tiefe neu berechnet wurde. Da das obere Array nun die Werte des unteren Arrays übernimmt, ist es sinnvoll eine weitere Tauschvariable einzuführen. Da dies geschehen soll, wenn i+1=n, bietet sich eine Variable der Form i-n an. Falls diese den Wert -1 annimmt, soll die Wertübernahme vollzogen werden. Wenn dies erreicht ist, ist Bubblesort bereits vollkommen realisiert, da die gestaffelten Zellen nur dann operieren sollen, wenn i den für sie richtigen Wert annimmt. Das Sortieren wird also nur bis zu jenem i ausgeführt, welches 1 nah an n herankommt. Dies haben wir bereits durch unsere Iterationsbox bereitgestellt. Nun können noch einige optische Verbesserungen durchgeführt werden, um die Vergleiche und Tauschungen besser zu visualisieren.
Insgesamt ergibt sich somit eine folgende Ansicht: Wir gehen vom Worst-Case-Szenario aus und wollen die Werte sortieren:
Nach einem Durchlauf für n sieht das Array bereits so aus:
Die 9 wurde in diesem Fall also bereits korrekt an die hinterste Stelle getauscht. Des Weiteren erkennt man, dass die 8 und die 7 für n=8 und i=0 rot markiert wurden. Dies sind die beiden Elemente, die gerade verglichen werden. In der ersten diagonalen Zeile wurden die beiden Elemente bereits getauscht. Im nächsten Schritt sollten nun die 8 und die 6 verglichen und ebenfalls getauscht werden:
Fazit
[Bearbeiten]Insgesamt ist die lauffähige Version in Excel dann eine sehr gute Simulation von Bubblesort, da die einzelnen Schritte des Algorithmus nach und nach in selbst gewählter Geschwindigkeit durchgesprochen werden können. Hierfür eignet sich das Projekt bereits in niedrigeren Klassenstufen, sobald Sortieralgorithmen angesprochen wurden. Eine tatsächliche Implementierung des gesamten Verfahrens, als Aufgabe für einen Schüler ist vermutlich zu zeitintensiv. Deshalb ist es – wie bereits erwähnt – sinnvoll, einzelne Teilprogramme vorzugeben oder die Schüler lediglich an der laufenden Simulation arbeiten zu lassen. Hierbei könnte der Lehrer sich dann Fragen überlegen, die von den Schülern beantwortet werden sollen, wie zum Beispiel „Welches ist das schlechteste Array, das man zum Sortieren heranziehen kann?“ oder „Welche Wertepaare werden im ersten (zweiten, dritten) Durchlauf des Algorithmus miteinander verglichen?“.
Eine lauffähige Version finden Sie hier: Bubblesort (von David Baumgärtel).
Eine kurze Anleitung zu dem Programm finden Sie hier: Anleitung (von David Baumgärtel).
Einzelnachweise
[Bearbeiten]- ↑ Pomberger, G. & Dobler,H. (2008). Algorithmen und Datenstrukturen. S.298
- ↑ Köthe,U. Vorlesung Algorithmen und Datenstrukturen.
- ↑ Für Aufzählung siehe: Pomberger, G. & Dobler,H. (2008). Algorithmen und Datenstrukturen. S.315
- ↑ Pomberger, G. & Dobler,H. (2008). Algorithmen und Datenstrukturen. S.316
Literatur
[Bearbeiten]- Pomberger, G. & Dobler,H. (2008). Algorithmen und Datenstrukturen. Eine systematische Einführung in die Programmierung. München: Pearson Studium.
- Balzert, H. (2005). Lehrbuch Grundlagen der Informatik. Konzepte und Notationen in UML 2, Java 5, C# und C++, Algorithmik und Software-Technik, Anwendungen. (2., durchgesehene Auflage der deutschen Ausgabe). München: Spektrum.
- Köthe, U. (2012). Vorlesung Algorithmen und Datenstrukturen. http://alda.iwr.uni-heidelberg.de/index.php/Sortieren (Stand: 7.2.2013)
Komplexe Funktionen
[Bearbeiten]Häufigkeit
[Bearbeiten]Die „HÄUFIGKEIT“ ist eine statistische Funktion, welche eine Häufigkeitsverteilung als vertikale Matrix zurückgibt. Unter http://www.learn-line.nrw.de/angebote/eda/medio/tipps/haeufigkeiten.htm ist eine Beschreibung zu finden, wie man mit Excel Häufigkeiten bestimmen kann.
Ausgabe des Syntaxbaums
[Bearbeiten]Zitat aus Wikipedia: "Ein Syntax-, Ableitungs- oder Parsebaum ist ein Begriff aus der theoretischen Informatik und bezeichnet eine baumförmige Darstellung einer Ableitung."
Zitat aus [...]
- Zitate dürfen nicht komplette Texte sein - weshalb formulieren Sie einfach selbst einen eigenen Text oder verlinken auf die andere Seite? --Cspannagel 00:13, 9. Jan. 2009 (CET)
Schieberegler
[Bearbeiten]Was ist ein Schieberegler?
Durch Anklicken der Pfeile links und rechts des Schiebereglers oder durch Verschieben des Schiebers mit der Maus kann in der Wert einer definierten Zelle („LinkedCell“) verändert werden. Die „LinkedCell“ wird im Eigenschaftsfenster des Steuerelements „Schieberegler“ oder „ScrollBar“ festgelegt. Schieberegler stehen vielen Programmen zur Verfügung. Im Folgenden werde ich die Verwendung eines Schiebereglers in „EXCEL“ beschreiben. In EXCEL verwendet man den Schieberegler dazu um Parameter einer Funktion zu verändern. Dabei muss der jeweilige Wert „Value“ des Schiebereglers mittels der „LinkedCell“ (z.B. Tabelle1!A1) in eine Formel integriert werden. Durch verschieben des Reglers ändern sich dann automatisch die Werte einer Wertetabelle und ein dazugehöriges Diagramm wird fortlaufend erneuert. Bei den heutigen schnellen Rechnern entsteht der Eindruck einer filmartigen Animation.
Wie erstelle ich einen Schieberegler in Excel 2007?(nicht Office für mac)
1. Öffne in Excel eine neue Datei (Arbeitsmappe) und gehe in die Tabelle in der ihre Berechnungen stattfinden sollen. Wähle im Menü Entwicklertools > Einfügen. Es öffnet sich die entsprechende Symbolleiste mit einer Palette von Steuerelementen. Diese Steuerelemente sind vordefinierte Objekte welche bestimmte Eigenschaften und Methoden besitzen. Man bezeichnet diese Objekte auch als „Werkzeuge“, mit denen man die Fähigkeiten von Excel erweitern kann. Eines dieser Objekte Ist die „ Bildlaufleiste“.
2. Wähle mit der Maus das Symbol aus und gehe mit der Maus an die Stelle deines Tabellenblatts an der der linke Rand deines Schiebereglers liegen soll. Danach ziehst du ein Rechteck auf und legst so die Größe deines Schiebereglers fest. (Dies Lage (Top und Left) und Größe (Height und Width) des Schiebereglers können exakter im Eigenschaftsfenster des Schiebereglers definiert werden.
3. Tipp: Mit gleichzeitig gedrückter ALT-Taste wird der Schieberegler entlang von Zeilen- und Spaltenlinien ausgerichtet, diese scheinen sich „magnetisch“ zu verhalten.
Wie stelle ich Eigenschaften des Schiebereglers ein?
Gehe zuerst in das Menü Entwicklertools. Dort klickst du auf den Menüeintrag „Entwurfsmodus “ in der Menüliste. Klicke mit der rechten Maustaste in die Fläche des Schiebereglers. Es öffnet sich ein Menü, aus dem du den Punkt „Eigenschaften“ wählst.
Hier die wichtigsten Eigenschaften:
BackColor: ändert die Hintergrundfarbe des Schiebereglers
Enabled: blockiert den Schieberegler (Der Schieber und die Richtungspfeile lassen sich nicht mehr benutzen)
ForeColor: ändert die Farbe der oberen Elemente (Schieber und Richtungspfeile rechts und links) auf dem Schieberegler
Height: ändert die Höhe des Schiebereglers
LargeChange: ändert die Schrittweite bei Klick auf den rechten (linken) Bereich vor den Enden der Bildlaufleiste (z.B. 10).
Left: Lage des Schiebereglers vom linken Rand des Tabellenblatts
LinkedCell: Die Zelle auf dem Arbeitsblatt, die die Werte (Eigenschaft Value) der Bildlaufleiste aufnehmen soll, z.B. die Zelle „A1“
Max: Der größte Wert, der eingestellt ist, wenn der „Schieberegler“ ganz rechts steht, z.B. 100.
Min: Der kleinste Wert, der eingestellt ist, wenn der „Schieberegler“ ganz links steht, z.B. 1.
MousePointer: ändert das Aussehen des Cursors beim Überstreichen des Schiebereglers
Orientation: ändert den Schieberegler (nach unten-oben / nach links-rechts)
PrintObject: Wert „true“ der Schieberegler wird gedruckt oder Wert “false“ der Schieberegler wird nicht gedruckt
ProportionalThumb: gibt an, ob sich die Größe des Bildlauffeldes proportional zum Bildlaufbereich verhält oder immer konstant ist
Shadow: zeigt den Schatten des Schiebereglers
SmallChange: zeigt Schritte des Schiebers
Top: Lage des Schiebereglers von oben
Value: zeigt Wert an dem sich der Schieber des Schiebereglers gerade befindet
Visible: macht den Schieberegler unsichtbar
Width: ändert die Länge des Schiebereglers Beenden: Mit einem weiteren Klick auf „Entwurfsmodus“ ist die Bildlaufleiste einsatzbereit und kann getestet werden. Sollten später Einstellungen verändert werden, ist über das gleiche Symbol wieder der Entwurfsmodus einzuschalten.
Funktionalität: Der Wert des Schiebereglers ist in der Eigenschaft „Value“ des Schiebereglers gespeichert. In der „LinkedCell“ ist dieser Wert sichtbar. Wenn man den Schieberegler nach links oder nach links schiebt, verändert sich auch den Wert in der „LinkedCell“. Bei dem Erstellen einer Wertetabelle gemäß einer Funktion wird ein Parameter der Funktion durch die Werte der „LinkedCell“ verändert.
Beispiel:
1. Geschwindigkeit-Zeit-Gesetz: V=a*t
„a“ ist Beschleunigung, „t“ Beschleunigungszeit, „v“ Geschwindigkeit.
Die Beschleunigung ist konstant. Der Wertebereich für die Beschleunigung liegt zwischen 0,1m/sec und 1m/sec. Dieser Wertebereich wird im Schieberegler (Min=0,1 Max=1) festgelegt. Mit dem Schieberegler kann man Beschleunigung (a) verändern. Es werden Werte von 0,1 bis 1 in 0,1-Schritten benötigt. Als „LinkedCell“ sei A1 eingetragen. In den Eigenschaften der Bildlaufleiste wird bei „Min“ 0 eingetragen und bei „Max“ 1. Im Tabellenbereich A3 bis A63 (A3:A63) ist die Beschleunigungszeit („t“) in Sek. angegeben. Im Tabellenbereich B3 bis B63 (B3:B63) wird jeweils der Wert der „LinkedCell“ A1 übernommen. Im Tabellenbereich C3 bis C63 (C3:C63) wird die Geschwindigkeit in Km/Stunde die mit der Formel Geschwindigkeit v = Beschleunigung a * Beschleunigungszeit t berechnet werden. Im Bereich (C3:C63) stehen folgende $A$1 * Ai * 3,6 dargestellt. Hierbei nimmt i die Werte 3…63 an! Es ist darauf zu achten, dass der Zellbezug $A$1 mit dem $-Zeichen versehen wird damit er beim Kopieren der Formel nach unten unverändert bleibt!
2. Darstellung des Grafen bei Funktionen erster , zweiter und dritter Ordnung.
Funktionsgleichung: y = ax.
Die Basiswerte a nehmen die Werte -5 bis +5 in Einer-Schritten an. Der Exponent x wird durch Schieberegler verändert. Minimaler Wert = 1 (Eigenschaft: Min 1), maximaler Wert = Max 3 (Eigenschaft: Max 3) . Der jeweilige Wert des Schiebereglers wird in der „LinkedCell“ B1 dargestellt. Die Funktionswerte y werden durch die Formel = Potenz ( $Ai;$B$1) in den Zellen B2 bis B14 Dargestellt. Hierbei nimmt i die Werte 1…3 an! Es ist darauf zu achten, dass der Zellbezug $B$1 mit dem $-Zeichen versehen wird damit er beim Kopieren der Formel nach unten unverändert bleibt! Der Graf verändert sich von einer Geraden bei x=1 zu einer Parabel bei x=2 und zu einer Hyperbel bei x=3.
Boxplots
[Bearbeiten]Hier findest du eine super Seite mit sehr guter Anleitung (Schritt für Schritt).
http://www.learn-line.nrw.de/angebote/eda/medio/tipps/boxplot_details.htm
Online-Tabellenkalkulation
[Bearbeiten]Neben der kostenlosen Open-Office-Version für Tabellenkalulation gibt es auch freie Online-Tabellenkalkulationsprogramme. Im Folgenden sei „Zoho-Sheet“ als Beispiel herangezogen (siehe www.zoho.com). Nach einem kurzen und kostenlosen Log-In gibt es hier nicht nur die Möglichkeit mit einer Tabellenkalkulation zu arbeiten, die nahezu an fast alle der standardmäßig verwendeten Möglichkeiten einer teuren Tabellenkalkulation wie Excel herankommt, sondern auch mit mehreren registrierten Usern gleichzeitig an einem Projekt zu arbeiten. Im Folgenden sind weitere Pro- und Contra-Argumente einer solchen Variante im Vergleich zu Excel und der Open-Office-Version stichpunktartig aufgezählt:
Gut:
- kostenlos
- mehrere Personen können gleichzeitig an einem Projekt arbeiten
- Import-Möglichkeit von Excel- und Open-Office-Arbeitsblättern
- ähnlicher Aufbau wie bei Excel von Menüleiste her und mit mehreren Arbeitsblättern
- sehr viele Möglichkeiten und Funktionen wie bei Excel (z.B. Funktion einfügen, Diagramm erstellen usw.)
- Online-Nutzung und dadurch in verschiedene andere Websites direkt einbettbar
- bei Einbettung in andere Websites ist bei einer Änderung des Projekts gleich die Aktualisierung vorhanden
Nachteile:
- nur online nutzbar
- Arbeitsgeschwindigkeit abhängig von Internetverbindung
- keine Hilfe-Funktion – nur Forum
(leider war beim gemeinsamen Arbeiten am Projekt nach einem Test zu Zweit noch nicht von beiden Seiten aus sofort die jeweilige Änderung des anderen sichtbar, sondern nur immer von einer Seite aus! Hoffe, das ging nur mir bei dem Testlauf so….)
Tipps zur Diagrammerstellung
[Bearbeiten]- Welches Diagramm kann ich im Bezug auf welche Fragestellung verwenden?
- Warum nutzt man die 3D-Darstellung eines Diadramm niemals? Und wann vielleicht doch?
--UlrikeKleinau 10:58, 19. Dez. 2008(CEST)
Spiele mit der Tabellenkalkulation
[Bearbeiten]Schiffe versenken
[Bearbeiten]Grundidee
[Bearbeiten]Bildbearbeitung mit der Tabellenkalkulation
[Bearbeiten]Im Rahmen der Veranstaltung Einführung in die Medieninformatik an der PH Heidelberg im Sommersemester 2012 werden wir hier unsere Überlegungen veröffentlichen, wie man mittels der Tabellenkalkulation Ideen der Bildbearbeitung verdeutlichen kann.--M.g. 11:25, 18. Mai 2010 (CEST)
Vektorgrafik mit Tabellenkalkulation
[Bearbeiten]- Könnte man nicht mal versuchen, 3D-Szenen mit Tabellenkalkulation zu modellieren? Und dann drehen / beleuchten / skalieren... lassen?
- Bedingung ist allerdings, dass kein VBA eingesetzt wird (Ehrenkodex der reinen Excellehre). Bisher habe ich 3D-Objekte als Kantenmodelle im Punktdiagramm darstellen lassen. Das Ausfüllen von Flächen wird da schwierig. Aber vielleicht hat ja jemand eine Idee.--M.g. (Diskussion) 22:17, 14. Mär. 2012 (CET)
- Sowas mit reinem Excel und ich spendiere einen 6er-Kasten Weizenbock (6 1-Liter-Flaschen) von der Brauerei zum Klosterhof Heidelberg. --M.g. (Diskussion) 22:27, 14. Mär. 2012 (CET)
Pixelgrafik mit Tabellenkalkulation
[Bearbeiten]- Grundprinzip: "Was die Pixelgrafiken anbelangt, werden die Zellen eines Kalkulationsblattes die Rolle der Pixel übernehmen und per bedingter Formatierung zu Bildern zusammengesetzt werden."
- Vorteile: a) Man muss die Daten nicht jedes Mal "einlesen" - sie liegen in den Tabellenzellen vor. (natürlich müssen sie da erst mal reinkommen) b) Die Daten werden räumlich am selben "Ort" visualisiert (durch Zellfarbe).
- Man könnte nun die Anwendung von Filtern, die Umwandlung von Farben nach Graustufen, Änderung von Helligkeit/Kontrast usw. formelmäßig implementieren und die Ergebnisse jeweils auf einem neuen Tabellenblatt darstellen. Dann sieht man die unterschiedlichen Bildvarianten, wenn man von Tabellenblatt zu Tabellenblatt "hüpft". --Cspannagel (Diskussion) 20:02, 14. Mär. 2012 (CET)
- Nicht kompliziert wäre auch Bildkomposition. Wem es dann nicht genügt, nur linear zu interpolieren, kann sich ja auch etwas trickreicheren Verfahren zuwenden, vielleicht: Cross Dissolve Without Cross Fade. --O.tacke (Diskussion) 10:52, 15. Mär. 2012 (CET)
- Super! Vielen Dank für die Arbeit. --M.g. (Diskussion) 12:29, 15. Mär. 2012 (CET)
- Man könnte sicher auch Komprimierungsverfahren (GIF mit Farbtabelle, JPEG u.ä.) simulieren.
- Kantenerkennung, automatisches "Füllen" von Bereichen wäre auch ne nette Idee...
Was sollten Schüler im Rahmen einer informationstechnischen Grundbildung über Bildbearbeitung und Computergrafik wissen
[Bearbeiten]Vielen Dank für die Ideen, die bisher hier eingetragen wurden. Falls Ihr auch Argumente habt, warum Ihr die einzelnen Punkte für wichtig hinsichtlich einer Vermittlung von Elementen der Informatik mit allgemeinbildendem Charakter haltet, schreibt doch bitte die Elemente mit dazu.--M.g. (Diskussion) 17:20, 16. Mär. 2012 (CET)
- Unterschiede Vektorgrafik - Pixelgrafik
- Was sind die jeweiligen Objekte?
- Eigenschaften (Skalierbarkeit, nachträgliche Veränderbarkeit usw...)
- Vektorgrafik vs. Pixelgrafik: Vor- und Nachteile der beiden Repräsentationsarten von Bildinformationen, wichtig für Medienkompetenz: Kompetenz der Entscheidung für eine jeweilige Grafikart im Rahmen von verschiedensten Präsentationen.--M.g. (Diskussion) 17:28, 16. Mär. 2012 (CET)
- Umwandelung: Speziell Vektorgrafik in Pixelgrafik, denn letztlich passiert das immer auf dem Bildschirm (auch dann, wenn eine Vektorgrafik vorliegt, wird diese in Bildpunkten dargestellt).
- Projektion 3D -> 2D. Wie schafft man es, dass ein 3D-Computerspiel auf einem 2D-Monitor dargestellt wird und das Ganze trotzdem 3D aussieht?
- Was passiert in der jeweiligen Repräsentation, wenn man ein Bild dreht / spiegelt / ...?
- Codierung von Farben
- gut im Kontext mit Stellenwertsystemen (Hexadezimalsystem, Binärsystem)
- Verschiedene Farbmodelle (RGB, CMYK, ...) und Umwandlung
Zahlendarstellung und Hamming-Code
[Bearbeiten]Im folgenden Kapitel wird eine Möglichkeit aufgezeigt zur Einführung von unterschiedlichen Zahlensystemen und des Hamming-Codes mit Hilfe der Tabellenkalkulation.
Zahlendarstellung
[Bearbeiten]

Eine Möglichkeit, um die neue Zahlensysteme (Binär-, Oktal-, Hexadezimalsystem) einzuführen ist, eine Verknüpfung vom Dezimalsystem und der Fingeranzahl der Menschen zu erstellen. Diese Verknüpfung wird dann ausgebaut, beispielsweise durch die Frage, wie Donald Duck oder Homer Simpsons mit vier Finger zählen würde. Als Hilfestellung kann die Klasse daran erinnert werden, dass das Dezimalsystem ein Positionszahlensystem ist. Das bedeutet, der Wert einer Ziffer hängt davon ab, an welcher Position in der Zahl sie steht. Je weiter links, umso größer ist die Zahl. Als Beispiel kann hier eine beliebige Zahl gewählt und diese dann entsprechende zerlegt werden. Wie hier am Beispiel der Zahl 543
Als nächstes sollte ein Beispiel gebracht werden, in dem eine Menge von Dingen mithilfe des Oktalsystems abgezählt wird, um die Klasse langsam mit dem neuen Zahlensystem vertraut zu machen. In Anschluss daran wird die Frage gestellt, ob nur die Ziffern 0 und 1 ausreichend sind, um die gleiche Menge abzuzählen.
Als nächstes kann jetzt eine beliebige Zahl im Okal- oder Binärsystem gewählt werden, um diese wie im Beispiel mit der Zahl 543 im verwendeten Zahlensystem zu zerlegen und in das Dezimalsystem umzurechnen. Somit können die Schüler eine Zahl in einem beliebigen Zahlensystem auf das Dezimalsystem umrechnen. Um eine Dezimalzahl in ein beliebiges Zahlensystem umzurechnen empfiehlt sich das Horner-Schema. Der erste Schritt um auf das Horner-Schema zu kommen, kann über den Euklidischen Algorithmus sein. Diesen führt man mit der Klasse am besten einmal aus.
Hier am Beispiel der Zahl 23 ausgeführt.
Im Anschluss daran wird die Idee verwendet, nicht die größte Potenz der Zahlenbasis erraten zu müssen, für welche die umzuwandelnde Zahl noch größer ist, sondern durch Verwendung des Horner-Schemas eine einfache Division, mit immer der gleichen Zahl, den Algorithmus vereinfacht. Hierfür wird veranschaulicht, was der Euklidischen Algorithmus im binären Zahlensystem macht. Als erstes wird eine Ganzzahldivision durchgeführt, was im Binärsystem wie folgt dargestellt werden kann.
Dieses Vorgehen wird sukzessive durchgeführt bis zur 0. Der letzte Schritt zum Horner-Schema ist, die Schüler darauf aufmerksam zu machen, die rechte Seite des Terms umzuschreiben, sodass immer nur durch die Zahl 2 geteilt werden muss.
Zur Erstellung einer Excel-Tabelle zum Umrechnen der Zahlensystem sind nur grundlegende Excelfunktionen nötig. Unter nachfolgendem Link kann eine Excel-Tabelle gefunden werden bei der die Umrechnung von Zahlensystem umgesetzt ist. (Link kommt noch)
Hamming-Code
[Bearbeiten]Eine Möglichkeit Codes im Unterricht einzuleiten, wäre über das Spiel Stille Post. Die Schüler können hier aus eigener Erfahrung nachvollziehen, wie schwer die Übertragung von Nachrichten eigentlich ist. Der nächste Schritt zum Hamming-Code ist, zunächst mit der Klasse beliebige Binärcodes für Buchstaben zu überlegen. Durch unterschiedliche Codebeispiele kann hervorgehoben werden, dass es Codes fester Länge gibt und Codes variabler Länge. Im Anschluss daran kann der Gedankenanstoß gebracht werden, was passiert, wenn ein Bit umgekippt ist und somit der Begriff der Hamming-Distanz eingeführt werden. Als nächstes kann die Frage gestellt werden, ob es möglich ist dem Empfänger mitzuteilen, dass die Nachricht falsch übermittelt wurde. Die Lösung hierfür kann zunächst über ein einfaches Paritätsbit erfolgen, dass beispielsweise gesetzt ist, wenn die Anzahl aller gesetzten Bits ungerade ist. Weitergeführt wird das Beispiel damit, dass die Leitung sehr stark überlastet ist und es infolgedessen nicht möglich ist, die falsch übertragenden Nachrichten nochmals zu übertragen und der Code so abgeändert werden muss, dass ein Ein-Bitfehler korrigierbar ist. Beispielsweise wird folgender Code bestimmt.
00 11 = "A"
11 00 = "B"
Hier kann bei der Übertragung 1 Bit kippen und der Empfänger ist trotzdem noch in der Lage den Code richtig zu entschlüsseln. Im Anschluss daran stellt man den Hamming-Algorithmus vor. Daran angeknüpft führt man am besten ein Beispiel durch, bei dem man die Paritätsbits für ein Codewort bestimmt, ein Bit kippt und dann das Wort wieder decodiert. Unter nachfolgendem Link kann eine Excel-Tabelle gefunden werden bei der der Hamming-Code umgesetzt ist. (Link kommt noch)