Projektive Geometrie/Ausgangssituation

Einleitung

Die projektive Geometrie beruht als Teilgebiet der Geometrie auf der Projektion von Punkten, Geraden, Ebenen etc. von eine Raum $V_{1}$ in einen anderen Raum $V_{2}$ . Hervor ging die projektive Geometrie in der ersten Hälfte des 19. Jahrhunderts aus der perspektivischen Darstellung dreidimensionaler Gegenstände aus dem $V_{1}:=\mathbb {R} ^{3}$ in der zweidimensionalen Ebene $V_{2}:=\mathbb {R} ^{2}$ .

Verlust geometrischer Eigenschaften

Bei einer solchen projektiven Abbildung von geometrischen Objekten (wie Punkten und Geraden) gehen bei der Projektion ggf. geometrische Eigenschaften verloren (z.B. die Parallelität von Geraden). Macht man z.B. ein Foto von zwei parallelen Geraden im dreidimensionalen Raum (z.B. ein Schienenstrang), so erzeugt die bekannte perspektivische Verkürzung zwei nicht parallele Gerade auf dem Foto, die sich im Fluchtpunkt schneiden.

Eukldische Geometrie

Bei der Zentralprojektion aus der „gewöhnlichen“ euklidischen Geometrie in $V_{1}:=\mathbb {R} ^{3}$ in der zweidimensionalen Ebene $V_{2}:=\mathbb {R} ^{2}$ bleibt die Parallelität in der projektiven Geometrie im $V_{2}:=\mathbb {R} ^{2}$ nur bei bestimmten Geraden erhalten. Wir betrachten als Ausgangssituation zunächst die Zentralprojektion.

Zentralprojektion

Wir betrachten zunächst das Konstruktionsprinzip am Beispiel von zwei parallen Geraden:

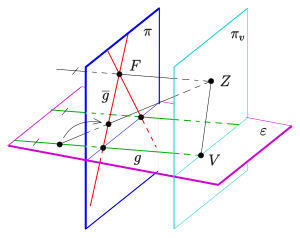
Erläuterungen zu Veranschaulichung

Der Betrachter beobachtet Objekte im dreidimensionalen $\mathbb {R} ^{3}$ von der Position $Z$ aus.
In der obigen Abbildung werden 2 parallele Geraden (grün) aus dem $\mathbb {R} ^{3}$ , bei beide in der violett markierten Ebene aus dem $\mathbb {R} ^{3}$ liegen.
Die projektive Ebene $\pi$ ist in der obigen Abbilding dunkelblau markiert und sei mit einem Koordinatensystem $\mathbb {R} ^{2}$ versehen.
Bildpunkte für Punkte aus $\mathbb {R} ^{3}$ existieren für einen Punkt $A=(x_{A},y_{A},z_{A})\in \mathbb {R} ^{3}$ in $\pi$ , wenn die Verbindungsgerade ${\overline {AZ}}$ einen Schnittpunkt mit $\pi$ besitzt.

Parallelprojektion

Eine Parallelprojektion einer Ebene auf eine andere erhält die Parallelität der Geraden. Bei einer Zentralprojektion (siehe Bild) ist dies i. A. nicht mehr der Fall. Im Bild werden die zwei grünen parallelen Geraden der horizontalen Ebene $\varepsilon$ durch die Zentralprojektion mit Zentrum $Z$ auf zwei sich im Punkt $F$ schneidende (rote) Geraden der senkrechten Ebene $\pi$ abgebildet. Der Punkt $F$ besitzt allerdings kein Urbild. Man nennt ihn den Fluchtpunkt der grünen Parallelenschar. Andererseits besitzt der Punkt $V$ (in der zu $\pi$ parallelen Ebene $\pi _{v}$ ) der Gerade $g$ kein Bild. Man nennt $V$ den Verschwindungspunkt der Gerade $g$ . Eine Zentralprojektion ist also keine Bijektion (1-1-Abbildung) der Ebene $\varepsilon$ auf die Ebene $\pi$ . Der Ausweg aus diesem Dilemma: Man fügt in jeder Ebene jeder Parallelschar einen weiteren Punkt hinzu, so dass sich parallele Geraden schneiden. Diese neuen Punkte nennt man Fernpunkte und die Menge der Fernpunkte bildet die Ferngerade der jeweiligen Ebene. Im Bild wird dann der Fernpunkt der Gerade $g$ auf den Fluchtpunkt $F$ abgebildet. Der Verschwindungspunkt $V$ wird auf den Fernpunkt der (roten) Gerade ${\overline {g}}$ abgebildet. Durch das Hinzufügen der Fernpunkte zu einer Ebene entsteht eine neue Inzidenzstruktur mit den typischen Eigenschaften

(Z1) Je zwei Punkte haben genau eine Verbindungsgerade und
(Z2) Je zwei Geraden haben genau einen Schnittpunkt.

Man nennt diese neue Struktur die reelle projektive Ebene.
Diese Art, eine affine Ebene zu erweitern, nennt man projektiv abschließen.

Siehe auch

Perspektivisches Zeichnen