Geogebra/Perspektivisches Zeichnen

Einleitung

Diese Seite können Sie als Wiki2Reveal-Präsentation in Vorträgen nutzen, um das perspektives Zeichnen mit Fluchtpunktperspektive zu erläutern (siehe Wiki2Reveal).

Aufgabe für Lernende

Die Aufgaben gliedern sich in die folgenden Bereiche

Theoretischer Hintergrund
Geogebra-Konstruktion
Projektion von Kreisen
Projektion von Kreisen
Projektion von einer Sinuskurve

Theoretischer Hintergrund

Analysieren Sie den theoretischen Hintergrund^[1] für das perspektivische Zeichnen^[2], bei dem als nicht-digitale Umgebung ein Spiegel als Projektionsfläche verwendet wird, auf den z.B. mit einem Folienstift das perspektivische Bild eingezeichnet wird.

Fluchtpunktperspektive

Die Fluchtpunktperspektive ist eine Möglichkeit des perspektivischen Zeichnens. In dem folgenden Foto sind mehrere Einzelbilder überlagert worden.

Perspektivische Zeichnen in der Kunst

Geogebra-Konstruktion

Ausgehend von dieser Situation des perspektivischen Zeichnens von Objekten auf einem Spiegel werden nun die Konstruktionen in Geogebra behandelt:

Z-Konstruktion für die Projektion von Halbgeraden,
X-Konstruktion für die Projektion von Punkten als Schnittpunkt von zwei Halbgeraden. Dabei wird der Bildpunkt über zwei Z-Konstruktionen generiert.
I-Konstruktion für die Projektion einer senkrecht stehenden Strecke, die über zwei X-Konstruktionen erzeugt wird.

Projektion von Kreisen

Überlegen Sie, wie Sie mit einer Ortslinie und einer X-Konstruktion das projektive Bild eines Kreise erstellen können.

Projektion von einer Sinus-Kurve

Überlegen Sie, wie Sie mit einer Ortslinie und einer X-Konstruktion das projektive Bild einer Sinuskurve in der Standebene erstellen können. Zeichnen Sie zunächst den Graphen der Abbildung:

f(x)=a\cdot \sin(x-b)+c

für geeignete Parameter $a,b,c\in \mathbb {R}$ . Verwenden Sie für diese Parameter Schieberegler.

Einführung

Bei dieser Lernressource geht es um die perpective Zeichnung von 3D-Objekten auf einem Spiegel und um die geometrischen Prinzipien der Konstruktion. Zusammen mit dieser Lernressource ein GitHub-Repository mit Geogebra-Dateien^[3] wurde erstellt, die mit dynamischer Geometrie-Software geöffnet werden kann Geogebra. Die Konstruktion basiert auf einem deutschen Artikel in der Zeitschrift Mathematica Didactica 26 (2003) Bd.1 43, Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Engelbert Niehaus^[4]

3D Konstruktion von Projektionen in Geogebra

Das Repository enthält Geogebra-Dateien zum Erlernen von 3D-Projektionen auf einem Spiegel Z-, X- und I-Konstruktion von 3D-Punkten und Linien. Dieses Repository verfügt über zusätzliches Lernmaterial für die Open Source Software Geogebra und die Datei ist in einem GitHub Repository gebündelt, das ursprünglich für die englische Lernressource Perspective Drawing on Mirror erstellt wurde.

3D-Konstruktion von Projektionen in Geogebra

Das folgende Bild zeigt die Grundsituation einer 3D-Projektion auf einem Spiegel. Das perspektivische Bild der Box ist auf den Spiegel gemalt.

Grundlegende Situation vor dem Spiegel

Verwenden Sie ein Papier als Vermittler zwischen der 3D-Welt und der 2D-Konstruktion.

Bemerkung - Konstruktion auf Papier

Das in der obigen Abbildung sichtbare DIN-A4-Blatt können Sie als Vermittler zwischen der 3D-Welt in der Standebene und der 2D-Projektion auf dem Spiegel verwenden.

das Papier repräsentiert Elemente aus Standebene der Objekt und
aus Projektionsebenen auf dem Spiegel-

Durch das Aufklappen erscheinen die wesentlichen Konstruktionselemente (wie Spurgerade, Horizont und Augenpunkt) auf dem Papier und der Bezug zur 3D-Situation vor dem Spiegel wird hergestellt.

Grundlegende Konstruktionselemente

(Standebene) Entspricht dem Brett in dem Foto, auf dem die Box im 3D-Raum positioniert wurde.
(Projektionsebene) entspricht dem Spiegel
(Spurgerade) Ist die Gerade, in der sich die Standebene (Brett) und Projektionebene berühren (Notation: $s$ )
(Horizont) ist eine Parallele zur Spurgeraden in der Projektionsebene in Augenhöhe des Betrachters (Notation: $h$ )
(Augenpunkt) Ist der Punkt im 3D-Raum an dem sich das Auge der Betrachterin befindet.
(Zentrum) Das Zentrum $Z$ ist der Punkt in der Projektionsebene, der den Augenpunkt in der Projektionsebene repräsentiert.

Konstruktion

Die perspektivische Zeichnung erzeugt ein Bild eines Objekts vor einem Spiegel. Das Auge beobachtet das projektive Bild von einem Punkt Z aus. Angenommen, der Betrachter malt das perspektivische Bild einer vertikalen Stange auf die Oberfläche des Spiegels.

Horizont und Spurgerade

Wir entfalten das Papier als Vermittler zwischen 2D-Projektionsebene auf dem Spiegel und 3D-Raum der Standebene. In Konstruktion erscheinen die beiden schwarzen parallelen Linien als Spurgerade und als Horizont. Übertragen diese Faltung auf zwei parallele Linien in Geogebra.

Z-Konstruktion für Halbgerade in der Ebene

Wir entfalten den Papiervermittler zwischen 2D und 3D Konstruktion und übertragen die Faltung auf zwei parallele Linien in Geogebra. Eine Z-Konstruktion erzeugt perspektivisches Bild einer Halbgerade.

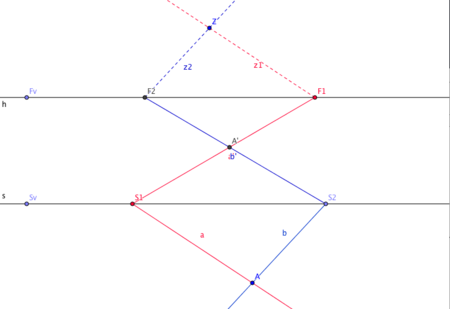
X-Konstruktion für Punkt in der Standebene

Die X-Konstruktion erzeugt ein perspektivisches Bild eines Punktes, der als Schnittpunkt von zwei Halbgerade eindeutig bestimmt ist. Der Bildpunkt ist damit durch zwei Z-Konstruktionen.

I-Konstruktion für eine vertikale Strecke

Eine I-Konstruktion erzeugt ein perspektivisches Bild einer vertikalen bzw. dem perspektivischen Bild eines Stabes auf dem Spiegel, der dann über zwei X-Konstruktionen als Bild der vertikalen Linie erzeugt wird.

3D-Objekt erzeugt mit Z-,X- und I-konstruktion

Ausgangssituation - Quader

Der dreidimensionale Quader steht auf dem Papier in der Standebene. Um die Fluchtpunktperspektive konstruktiv umzusetzen, wird zunächst die Standfläche auf dem Papier umrandet und die Senkrechten zu Standebene senkrecht zum vertikalen Papierrand gezeichnet. Dies ist das Ausgangbild des Quaders für die perspektische Konstruktion in der Bilddebene.

Bemerkung - Winkeltreue

Alle Polygone (Vielecke) in der Standebene, die in Ebenen parallel zur Standebene liegen, sind winkeltreu u. Im Beispiel mit dem Quader sind die Grundfläche und Deckfläche des Quaders Rechecke. Die Seitenfläche werden dabei als Parallelgramme dargestellt. Diese Winkeltreue trifft nicht mehr auf die Fluchtpunktprojektion in die Spiegelebene zu.

Bemerkung - Senkrechten

Eine Senkrechte wird in der Standebene parallel zum Papierrand gezeichnet. Die Projektion dieser senkrechten Geraden sind auch wieder senkrecht in der gespiegelten perspektivischen Fluchtpunktdarstellung.

Bemerkung - Winkeltreue in perspektivischer Darstellung

Die perspektivische Darstellung des Quaders ist allerdings nicht mehr winkeltreu für Vielecke, die in Ebenen parallel zur Standebene liegen.

Aufgaben

Pyramide
Kreis in der Standebene
beliebiger Kreis (trigonometrische Darstellung in der Standebene).

Die Lösungen zu diesen aufgaben finden Sie unter GitHub

Aufgabe - Pyramide

Konstruieren Sie eine Pyramide mit quadratischer Grundfläche in der gespiegelten Fluchtpunktperspektive! Die Seitenrläge des Quadrates sei $a$ . Die Spitze befindet sich in der Höhe $h=2a$ über der Standebene. Beschreiben Sie zunächst die wesentlichen Schritte für die Konstruktion die Spitze in der Standebene und konstruktieren Sie dann die gespiegelte Fluchtpunktperspektive der Pyramide.

Aufgabe - einzelne Punkte mit TKP

Betrachten wir nun erneut die perspektifische Spiegelung von oben. Erzeugen Sie z.B. mithilfe eines TKP ein Dokument, mit welchem Sie durch Eingabe der Posititionspunkte des Objektes dessen Spiegelpunkte in der x-z-Ebene darstellen können. \textbf{Hinweis:} Orientieren Sie sich dafür an der obigen mit GeoGebra erstellten Datei. Legen Sie zusätzlich den zu spiegelnden Punkt auf die y-Achse und bedenken Sie, dass diese nun in den dreidimensionalen Raum übertragen werden müsse (Falten des Blattes - ggf. Ämnderung der Koordinaten).

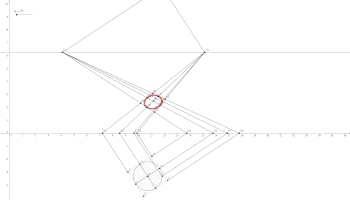
Aufgabe - Kreis

Konstruieren Sie einen Kreis in der Standebene. Verwenden Sie die X-Konstruktion aus dem Geogebra-Demodateien, um das gespiegelte perspektivische Bild zu zeichnen.

Aufgabe - Zylinder

Verwenden trigonometrische Funktionen, um zunächst die Bewegung auf einem Kreis mit einem Schieberegeler und Werten $t\in [0,2\pi ]$ in der Standebene umzusetzen. Verwenden Sie dann die I-Konstruktion um das Bild der 3D-Kreisbahn in der Höhe der Stablänge zu erzeugen. Erläutern Sie, wie das perspektivische eines Zylinders daraus entsteht!

Stereoskopie

Die räumliche Wahrnehmung muss mit Ihrer Umgebung interagieren und für geometrische und räumliche Lernziele relevant sein (z.B. in der Chemie^[5]. Die oben genannten Konstruktionen können auf Stereoskopie erweitert werden.

Lernaktivitäten - Stereoskopie

Analysieren Sie das stereoskopische Bild mit dem Baumstumpf bzgl. Unterschiede in der Projektion Kartierung von Objekten für das linke und rechte Auge.
Untersuchen Sie Anwendungen der Stereoskopie und die geschichtliche Entwicklung, wann die ersten Anwendungen der Stereoskopie genutzt wurden.

I-Konstruktion mit Stereoskopie

In der I-Konstruktion werden nun zwei perspektivische Bilder für das linke und rechte Auge erzeugt. Dabei entstehen Projektionen eines vertikalen Stabes in der Standebene auf dem Spiegel. Dabei werden zwei I-Konstruktionen für unterschiedliche Augenpunkte $Z_{L}$ und $Z_{R}$ erzeugt. Der Abstand der Augenpunkte (siehe Querdisparation).

Siehe auch

Externe Quellen

Orthogonalprojektion mit Würfelgebäuden mit Geogebra - von Anna Hundertmark

Seiteninformation

Diese Lernresource können Sie als Wiki2Reveal-Foliensatz darstellen.

Wiki2Reveal

Dieser Wiki2Reveal Foliensatz wurde für den Lerneinheit Geogebra' erstellt der Link für die Wiki2Reveal-Folien wurde mit dem Wiki2Reveal-Linkgenerator erstellt.

Die Seite wurde als Dokumententyp PanDocElectron-SLIDE erstellt.
Link zur Quelle in Wikiversity: https://de.wikiversity.org/wiki/Geogebra/Perspektivisches_Zeichnen
siehe auch weitere Informationen zu Wiki2Reveal und unter Wiki2Reveal-Linkgenerator.

Quellennachweis/Literatur

↑ Engelbert Niehaus (2003), Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Mathematica Didactica 26, Bd. 1 43, URL: http://mathematica-didactica.com/altejahrgaenge/md_2003/md_2003_1_Niehaus_Spiegelung.pdf (access 2020/11/24)
↑ D'amelio, J. (2004). Perspective drawing handbook. Courier Corporation.
↑ 3D-Konstruktion mit Geogebra (2017-2019) Engelbert Niehaus, URL: https://github.com/niebert/3D_Construction_Geogebra (zugegriffen am 2019.06.12)
↑ Niehaus, Engelbert (2003), Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Mathematica Didactica 26 (2003) Bd.1 43,
↑ Coleman, S. L., & Gotch, A. J. (1998). Spatial perception skills of chemistry students. Journal of Chemical Education, 75(2), 206.<

[1] Engelbert Niehaus (2003), Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Mathematica Didactica 26, Bd. 1 43, URL: http://mathematica-didactica.com/altejahrgaenge/md_2003/md_2003_1_Niehaus_Spiegelung.pdf (access 2020/11/24)

[2] D'amelio, J. (2004). Perspective drawing handbook. Courier Corporation.

[3] 3D-Konstruktion mit Geogebra (2017-2019) Engelbert Niehaus, URL: https://github.com/niebert/3D_Construction_Geogebra (zugegriffen am 2019.06.12)

[4] Niehaus, Engelbert (2003), Experimenteller Umgang mit Spiegelung und Perspektive unter Verwendung von Dynamischer Geometriesoftware, Mathematica Didactica 26 (2003) Bd.1 43,

[5] Coleman, S. L., & Gotch, A. J. (1998). Spatial perception skills of chemistry students. Journal of Chemical Education, 75(2), 206.<

[1]

[2]

[3]

[4]

[5]