AR VR in der Grundschule

Die folgende Lernressource befasst sich mit der Entwicklung von VR/AR-Anwendungen und deren möglichen Integration in Lernumgebungen^[1]. Der wesentliche Teil der Lernressource ist ein Einführungstutorial für die 3D-Modellierung mit A-Frame. Die Standardkonzepte wurden in einfacher Sprache erläutert und mit Minimalbeispielen belegt. Als nicht-triviales Beispiel wurde

die Sonne-Erde-Mond-Bewegung detailliert umgesetzt und
ein Modell^[2] der St. Maria Kirche in Landau

detailliert erklärt und implementiert.

Lernziel

Rotierendes Planetensystem auf Hiro-Marker

Nach Bearbeitung dieser Lernressource werden Sie in der Lage sein, selbst 3D-Objekt auf Markern zu konstruieren und diese digitale Objekte auch auf Markern zu animieren. Die Abbildung zeigt das Ergebnis der Lerneinheit. Die Lernumgebung selbst basiert auf dem Open Community Approach, bei dem Open-Source-Software und Open Educational Resources (OER) den freien Zugang zu den Bildungsressourcen ermöglichen und diese unter einer freien Licence für Lernpersonen und für Lernende anpassbar sind und wieder frei zur Verfügung dem Bildungssystem zur Verfügung gestellt werden können.

Vorbereitung

(Seite mit Markern) Drucken Sie dazu eine Seite mit Markern aus und zerschneiden Sie die Marker so, dass noch ein weißen Rand bleibt. Kleben Sie dann die Marker so auf eine Pappe, dass der Hiro-Marker auf der einen Seite und der Kanji-Marker auf der anderen Seite zu sehen ist. Diese Pappe ist dann für beliebige 3D-Modelle auf einem Hiro- oder Kanji-Marker verwendbar, da das Modell nicht im dem Marker kodiert ist, sondern nur die Erkennung der Position der 3D-Modells im Kamerabild verwendet wird. Kleben Sie die quadratischen Marker so auf eine rechteckige Pappe, deren Größe ausreichend ist, um die Pappe noch mit der Hand festzuhalten, ohne den Marker selbst mit der Hand zu verdecken.

Endprodukte

Wenn Sie einen ersten Eindruck von dem animierten Endprodukt haben möchten, dann wäre es sinnvoll zunächst einen Hiro-Marker auszudrucken und auf Pappe zu kleben.

(Planetensystem mit Hiro-Marker) Starten Sie dann mit Ihrem Webbrowser die Webseite mit einem rotierenden Planetensystem und erlauben Sie den Zugriff auf die Webcam. Das Endprodukt hat im Gegensatz zu Abbildung oben noch keine Texturen.
(3-D-Modell St. Maria Kirche geometrische Körper) Starten Sie dann mit Ihrem Webbrowser die Webseite mit einem 3-D-Modell der St. Maria Kirche und erlauben Sie den Zugriff auf die Webcam. Es wird ein 3-D-Modell der Kirche angezeigt und die darin enthaltenen geometrischen Körper erscheinen farbig auf dem Hiro-Marker.
(Hiro-Marker) Halten Sie nun den Hiro-Marker, den Sie auf die Pappe aufgeklebt haben in die Kamera und beobachten Sie die Rotation der Planeten.
(3D-Modelle auf Markers ausprobieren)

Erste Schritte

Formal wird A-Frame als Framework zur Darstellung von 3D-Objekten und VR-Inhalten im Web-Browser bezeichnet. A-Frame ist auf WebVR und WebGL Javascript Bibliotheken aufgebaut, jedoch basiert die Interaktion auf HTML-ähnlicher Sprache. Damit ist gemeint, dass A-Frame als eine Erweiterung von HTML gesehen werden kann, die eine zusätzliche Funktionalität besitzt. Sie kann 3D-Objekte erschaffen und sie im Browser erscheinen lassen. Die A-Frame-Anwendungen sind also im Grunde nichts anderes als Webseiten, auf die man per Web-Browser zugreifen kann. Der Inhalt kann auf allen möglichen Geräten per Web-Browser abgerufen werden, z. B. auf Handys, Tablets und Laptops. Zudem unterstützt A-Frame auch viele VR-Brillen wie HTC Vive, Oculus Rift, Windows Mixed Reality. Im Gegensatz zu WebVR- und WebGL-Anwendungen benötigt man für A-Frame keine Vorkenntnisse von Javascript. Daher ist A-Frame eine willkommene Lösung für Menschen, die sich nicht mit Programmierung auskennen. Das Framework ist ein Open-Source-Projekt und ist daher nicht kostenpflichtig. Beim Verfassen dieser Lernressource war die Version 1.1.0 die Aktuellste. Das muss beachten werden, da A-Frame nicht durchgängig abwärtskompatibel ist und daher einige Befehle aus diversen Tutorials nicht mehr benutzt werden können.

Es gibt verschiedene Möglichkeiten, mit A-Frame zu arbeiten. Behandelt werden die beiden folgenden Wege:

Glitch

Der einfachste und schnellste Weg ist Glitch. Glitch bietet eine Online-Plattform mit integriertem Code-Editor und vorinstallierten Paketen für die sofortige Entwicklung und das Hosting von A-Frame-basierten Webseiten. Mit Hosting ist das Platzieren der Webseiten (A-Frame-Anwendungen) auf einem externen Server gemeint. Ebenso liefert Glitch eine Menge Beispiele (Projekte) mit einem offenen und modifizierbaren Quellcode, die man sofort abrufen kann. Hiermit bietet Glitch einen sehr einfachen Start in die Entwicklung mit A-Frame.

JSON3D4Aframe und GitHub

JSON3D4Aframe und GitHub. JSON3D4Aframe bietet dabei einen einfachen Online-Editor für Aframe, um 3-D-Modelle aus vorprogrammierten geometrischen Figuren zu erstellen, direkt angezeigt zu bekommen und abzuspeichern. GitHub ergänzend dazu die Möglichkeit, diese auf einer Homepage zu hosten und von überall aus abzurufen.

Elementare Konzepte der A-Frame Modellierung

A-Frame basiert auf HTML-Sprache, daher sollte die Datei mit <!DOCTYPE html> Deklaration beginnen. In die typische Struktur einer HTML-Datei gehören <head>...</head> und <body>...</body>-Sektionen, auch Tag genannt. Die erste dient dabei als Container der Konfigurationsdaten; da steht beispielsweise der Titel, Style usw. Ebenso werden dort die dazu benötigten Skripte, unter anderem A-Frame, mithilfe von <script>...</script>-Tag angeknüpft. Die zweite Sektion ist ein Container der Daten, die später im Browser angezeigt werden. Der A-Frame-Inhalt wird innerhalb des <a-scene>...</a-scene>-Tags eingeführt. Das Beispielprogramm 1 zeigt die typische Struktur einer A-Frame-Datei. In dem Beispiel wird ein Würfel mithilfe eines <a-box>...</a-box>-Befehls gezeichnet.

Beispielprogramm 1

<!DOCTYPE html>
<html>
  <head>
    <script src="https://aframe.io/releases/1.1.0/aframe.min.js"></script>
  </head>
  <body>
    <a-scene>
      <a-box> </a-box>
    </a-scene>
  </body>
</html>

Das Gute an A-Frame ist, dass Befehle wie <a-box> vorhanden sind, womit man ganz einfach verschiedene geometrische Figuren darstellen kann, ohne Programmierkenntnisse von Javascript oder Ähnlichem zu benötigen. Im Späteren wird der Code nicht komplett angegeben, sondern nur die A-Frame-relevanten Abschnitte im <a-scene>...</a-scene> – um Platz zu sparen und den Fokus des Lesers auf das Wesentliche lenken zu können. Die nächsten Abschnitte behandeln die Modellierung von geometrischen Figuren, dabei wird auf Texturen, Animation und Hintergründe eingegangen.

Einfache geometrische Figuren

In A-Frame gibt es grundlegende Figuren, die man für die Ausarbeitung ganz einfach benutzen kann. Man unterscheidet zwischen 13 vorprogrammierten 2D- und 3D-Figuren. Bei 3D-Objekten hat man die Wahl zwischen Würfeln, Kegeln, Zylindern, Dodekaedern, Oktaedern, Tetraedern, Kugeln, Tori und Torusknoten. Für die 2D-Geometrie sind folgende Objekte vorprogrammiert: Ebenen, Kreise, Ringe und Dreiecke. Jedes dieser geometrischen Objekte besitzt interne Parameter, die die Geometrie des Objektes definieren, z. B. ist eine Kugel festgelegt durch den Radius und beim Zylinder wird zusätzlich die Höhe benötigt. Zusätzlich haben alle geometrischen Objekte globale geometrieunabhängige Eigenschaften wie Position, Rotation usw.

A-Frame benutzt das typische kartesische Koordinatensystem. Die Kamera ist positioniert in ${\textstyle (0,1.6,0)}$ mit Blick in die negative ${\textstyle z}$ -Richtung. Die Größen sind alle in Meter angegeben, sodass die Höhe der Kamera ${\textstyle 1.6m}$ beträgt und somit ungefähr auf Augenhöhe eines Menschen liegen soll. Beispielprogramm 2 zeigt eine grüne Kugel und einen roten Würfel, die in ${\textstyle (-1,1.6,-2)}$ und ${\textstyle (1,1.6,-2)}$ positioniert sind. Die ${\textstyle y}$ -Koordinate der Objekte ist gleich der Höhe der Kamera, und ${\textstyle z=-2}$ entspricht ${\textstyle 2m}$ Distanz von der Kamera in ${\textstyle z}$ -Richtung. Wie man aus dem Code erkennt, wurde eine Kugel vom Radius ${\textstyle 0.5m}$ erstellt und bei dem Würfel wurden die Dimensionen nicht angegeben, daher wurde ein Würfel mit Standardgrößen ${\textstyle 1m\times 1m\times 1m}$ erzeugt.

A-Frame bietet eine Menge der Transformationen wie z. B. Rotation oder Skalierung. Wie man im Beispielprogramm 3 sieht, wurde die Kugel durch leichte Modifikation in die ${\textstyle y}$ -Richtung gestreckt und der Würfel um ${\textstyle 45^{\circ }}$ um die eigene ${\textstyle y}$ -Achse gedreht. Hierbei ist es wichtig zu bemerken, dass bei einer Rotation die eigene lokale ${\textstyle y}$ -Achse durch den Mittelpunkt des Quadrats und nicht das globale Koordinatensystem benutzt wurde.

Beispielprogramm 2

<a-scene>
  <a-box position = "1 1.6 -2"  
         color="red"> 
  </a-box>
  <a-sphere radius="0.5"
            position="-1 1.6 -2" 
            color="green"> 
  </a-sphere>
</a-scene>

Beispielprogramm 3

<a-scene>
  <a-box position="1 1.6 -2"
         color="red" 
         rotation="0 45 0"> 
  </a-box>
  <a-sphere radius="0.5" 
            position="-1 1.6 -2" 
            color="green" 
            scale="1 2 1"> 
  </a-sphere>
</a-scene>

Das ist einer der wesentlichen Punkte in der Entwicklung mit A-Frame – man muss immer den Überblick behalten, welche Figuren bezüglich welcher Koordinatensysteme definiert sind. Um dies zu verdeutlichen, wird das Beispielprogramm 4 betrachtet. Dieses produziert beim ersten Hinschauen genau dasselbe Bild wie Beispielprogramm 2, allerdings ist hierbei die Kugel innerhalb des Würfels definiert, d. h. innerhalb des <a-box>...</a-box>-Tags. Somit ist die Kugel als Teil der Würfelgeometrie zu verstehen. Dieses Phänomen ist als Vererbung bekannt. Die Kugel vererbt unter anderem das Koordinatensystem des Würfels: Der ${\textstyle 0}$ -Punkt der Kugel ist mit dem Zentrum des Würfels bestimmt. Wie in Zeile 5 zu sehen ist, muss die Kugel um ${\textstyle 2m}$ in die ${\textstyle x}$ -Richtung verschoben werden, damit man dieselbe Geometrie bekommt, wie im Beispielprogramm 2. Die Kugel ist ein Teil der Würfelgeometrie, die Drehung des Würfels impliziert die Drehung der Kugel um die ${\textstyle y}$ -Achse des Würfels, wie im Beispielprogramm 5 zu sehen ist.

Beispielprogramm 4

<a-scene>
  <a-box position="1 1.6 -2" 
         color="red">
         <a-sphere radius="0.5" 
                   position="-2 0 0" 
                   color="green"> 
         </a-sphere>
 </a-box>   
</a-scene>

Beispielprogramm 5

<a-scene>
  <a-box position="1 1.6 -2"
         color="red"  
         rotation="0 -45 0">
         <a-sphere radius="0.5" 
                   position="-2 0 0" 
                   color="green"> 
         </a-sphere>
  </a-box>   
</a-scene>

Hiermit wird deutlich, wie man ein Objekt an die Achse eines anderen Objektes binden kann. Dies ist besonders wichtig, wenn man die Bewegungen des einen Objektes in Bezug auf das andere implementieren möchte. Allerdings ist noch zu klären, wie man ein Objekt bezüglich der Achse des anderen rotieren lässt, ohne dass das Andere selbst rotiert. Eine Möglichkeit, so etwas zu implementieren, ist die Zuhilfenahme von <a-entity>. Die Idee dahinter besteht darin, einen Platzhalter für ein Objekt zu kreieren, und analog zu Beispielprogramm 5 ein anderes Objekt um den Platzhalter rotieren zu lassen. Das statische Objekt wird einfach über dem Platzhalter positioniert. Beispielprogramm 6 zeigt eine Kugel, die bezüglich der ${\textstyle y}$ -Achse des Würfels gedreht ist, der Würfel jedoch nicht.

Beispielprogramm 6

<a-scene>
  <a-entity position="1 1.6 -2" 
            rotation="0 -45 0">
            <a-sphere radius="0.5" 
                      position="-2 0 0" 
                      color="green"> 
            </a-sphere>
  </a-entity>   
  <a-box position="1 1.6 -2" 
         color="red"> 
  </a-box>   
</a-scene>

So ein <a-entity>-Platzhalter kann ebenfalls nützlich sein beim Importieren der 3D-Objekte. Das Beispielprogramm 7 illustriert, wie man ein Objekt im gltf-Format in A-Frame importieren und richtig positionieren kann. Das Baum-Modell wurde von Don McCurdy heruntergeladen.

Beispielprogramm 7

<a-scene>
  <a-entity position="0 1.6 -5"
            gltf-model="tree.gltf">
  </a-entity>
</a-scene>

Der <a-entity>...</a-entity>-Tag ist ein Teil des sogenannten Entity-Component-System-Konzeptes (ECS). Das Konzept wird größtenteils für die Entwicklung von Computerspielen verwendet und trägt dieselbe Philosophie wie die objektorientierte Programmierung: Vererbung und Hierarchie. Es hat sich herausgestellt, dass die Aufbauart des Codes in vielen Aspekten sehr hilfreich sein kann. Wie man bereits gesehen hat, ist einer der wichtigsten Aspekte, dass die Objekte innerhalb der Entity ein lokales Koordinatensystem bekommen, und daher der Code unabhängig vom globalem Koordinatensystem ist. Wenn man an großen Projekten arbeitet, möchte man nicht alle geometrischen Objekte notwendigerweise im selben Ort bezüglich desselben Koordinatensystems deklarieren, sondern man möchte die Szene in mehrere solcher Entities teilen und getrennt bearbeiten.

Texturen

Der Zweck der 3D-Modellierung ist oft die Visualisierung der realistischen 3D-Objekte. Um diese so realistisch wie möglich gestalten zu können, werden gerne Texturen verwendet. Unter einer Textur versteht man ein Bild, das auf die Oberfläche der jeweiligen Figur projiziert wird, um physischen Stoff oder Material zu reproduzieren. Typische Beispiele sind Holz, Metall, Gestein, usw. Im Beispielprogramm 8 sieht man einen Würfel, der aussieht, als wäre er aus Backsteinen. Das Einfügen von Texturen wird mithilfe einer src-Option ausgeführt, wie es in Zeile 5 zu sehen ist.

Beispielprogramm 8

<a-scene>
  <a-box position="0 1.6 -1.3" 
         rotation="0 30 0"
         color="white"
         src="bricks.jpg">
  </a-box>    
</a-scene>

Beispielprogramm 9

<a-scene>
  <a-box position="0 1.6 -1.3" 
         rotation="0 30 0"
         color="white"
         src="bricks.jpg"
         normal-map="bricks_nm.jpg">
  </a-box>    
</a-scene>

Allerdings sieht die Backsteinoberfläche, wie man auf dem Bild sehen kann, ziemlich flach und somit künstlich aus. Um den visuellen 3D-Effekt zu erzielen, benutzt man sogenannte ”normal maps”. Mit ”normal mapping” bezeichnet man den Trick, der die Reflexion des Lichtes modifiziert, und somit der Oberfläche einen erhabenen Eindruck verpasst. Das Benutzen von normal maps ist im Beispielprogramm 9 dargestellt; dies passiert mit der normal-map-Option, siehe Zeile 6. Man kann beobachten, dass die Oberfläche viel realistischer aussieht. Die dazu benötigte Textur und normal map wurde von [1] heruntergeladen.

Es gibt viele weitere Optionen, die visuelle Erscheinung der Materialien zu verbessern. Dazu gibt es gute Tutorials in Pasquariello, wie die Dokumentation auf der A-Frame-Webseite [2] . Allerdings muss man noch eine Sache anmerken: Die Textur (das Bild) wird auf die komplette Fläche aufgeklebt und somit muss die Skalierung extra angepasst werden. Wenn der Würfel groß genug ist, sehen die Backsteine ebenfalls gigantisch und unrealistisch aus. Die Skalierung der Textur kann mit repeat implementiert werden, wie es im Beispielprogramm 10 gezeigt wird. Mit zwei Zahlen ist die Skalierung in die ${\textstyle x}$ - und ${\textstyle y}$ -Richtungen gemeint. Indem man in die eine Richtung mehr skaliert, können die Backsteine dicker bzw. dünner gemacht werden. In Beispielprogramm 10 wurde eine zweifache Skalierung in beide Richtungen vorgenommen. Hier muss man noch betonen, dass man die dazugehörige normal map entsprechend anpassen muss.

Beispielprogramm 10

<a-scene>
  <a-box position="0 1.6 -1.3" 
         rotation="0 30 0" 
         color="white" 
         src="bricks.jpg" 
         repeat="2 2"
         normal-map="bricks_nm.jpg"
         normal-texture-repeat="2 2">
  </a-box>    
</a-scene>

Beispielprogramm 11

<a-scene>
  <a-assets>
    <img id="bricks" src="bricks.jpg">
    <img id="bricks_nm" src="bricks_nm.jpg">
  </a-assets>
  <a-box position="0 1.6 -1.3" 
         rotation="0 30 0"  
         material="color:white;         
                   src:#bricks;
                   repeat:2 2;
                   normal-map:#bricks_nm;    
                   normal-texture-repeat:2 2">
  </a-box>    
</a-scene>

Oft werden die ganzen Materialerscheinungsoptionen in material definiert und die Bilder in <a-assets> eingeführt, siehe Beispielprogramm 11. Die Beispielprogramm 10 und Beispielprogramm 11 haben exakt den selben Effekt, allerdings wird beim zweiten mehr Struktur hervorgehoben, was den Code lesbarer macht. Ebenso ist die zweite Version kanonischer, wenn man dieselben Texturen mehrfach verwendet. Insbesondere die Vordefinition der Texturbilder als sogenannte Assets (Verwendete Dateien wie z. B. Bilder, Videos, Musik) sind für das Speichermanagement von Vorteil.

Einfache Dynamik

A-Frame funktioniert nicht nur gut bei der Erstellung der 3D-Objekte, sondern erlaubt auch gewisse Animationen. Die als Standard vorprogrammierten Animationen in A-Frame kann man in zwei Kategorien unterteilen: Bewegung und Erscheinung [3]. A-Frame erlaubt ebenfalls gewisse Interaktionen mit dem Nutzer; z. B. kann die Maus als Auslöser einer oder mehrerer Animationen dienen. Das wird hier aber nicht betrachtet.

Im Folgenden werden die vier Arten der Animation erklärt, die am wichtigsten sind: Rotation, Gradlinige Bewegung, Farb- und Formänderungen. Hierbei ist zu beachten, dass die Notation mit <a-animation>-Tag, wie sie in Pasquariello, benutzt wird, ab Version 0.9.0 nicht mehr möglich ist.

Beispielprogramm 12

<a-scene>
  <a-box color="red"
         position="0 0.6 -3"
         animation="property:rotation;
                    to:0 360 0;
                    easing:linear;
                    loop:true;
                    dur:5000">
  </a-box>    
  <a-sphere color="green"
            radius="0.5"
            position="-1 2.6 -3"
            animation="property:position;
                       to:1 2.6 -3;
                       easing:easeInOutSine;
                       dir:alternate;
                       loop:true;
                       dur:2500">
  </a-sphere>
</a-scene>

Einfache Bewegungs- animation 1
Einfache Bewegungs- animation 2

Im Beispielprogramm 12 sind zwei Animationsvorgänge dargestellt: Der Würfel rotiert um die eigene ${\textstyle y}$ -Achse und die Kugel bewegt sich von links nach rechts und zurück. Das Einführen der Animationen ist mit dem Stichwort <animation> umgesetzt, siehe Zeilen 4 und 13. Die Art der Bewegung wird mit <property> definiert; im Beispiel werden die Rotation und geradlinige Bewegungen betrachtet, die mit den Stichworten <rotation> und <position> gekennzeichnet sind. Das Stichwort <to> bezeichnet den Endzustand der Animation; beim Würfel wäre der Endzustand eine Rotation um ${\textstyle 360^{\circ }}$ um die ${\textstyle y}$ -Achse und bei der Kugel die Koordinate des Endpunktes. Das Stichwort <dur> gibt in Millisekunden an, wie lange die Animation dauern soll. In diesem Fall sind es ${\textstyle 5s}$ bei dem Würfel und ${\textstyle 2.5s}$ bei der Kugel. Mit <loop> kann man angeben, wie oft die Animation ablaufen soll. Wenn man den Wert auf <indefinite> setzt, wiederholt sich die Animation unendlich oft. Mit <easing> kann man die Geschwindigkeitsänderung der Simulation kontrollieren, z. B. mit linear bleibt die Geschwindigkeit konstant über den ganzen Simulationsvorgang, und mit <easeInOutSine> ändert sich die Geschwindigkeit sinusförmig, d. h. die Geschwindigkeit am Anfang und zum Schluss ist langsamer als in der Mitte. Die Bewegung der Kugel ist definiert von links nach rechts, d. h. nach einer Iteration springt die Kugel in den Anfangszustand. Damit das nicht passiert und die Kugel sich ”rückgängig” mit der selben Geschwindigkeit zum Anfangszustand bewegt, kann das Stichwort <dir:alternate> verwendet werden. Daher wurde die Simulationszeit der Kugel auf ${\textstyle 2.5s}$ gesetzt, denn sie braucht genau so lange auch zurück. In ${\textstyle 5s}$ , in denen der Würfel eine ganze Umdrehung macht, schafft es die Kugel also einmal hin und zurück.

Beispielprogramm 13

<a-scene>
  <a-box color="red"
         position="1 1.6 -2"
         animation="property:scale;
                    to:0.5 1 2;
                    easing:linear;
                    dir:alternate;
                    loop:true;
                    dur:5000">
  </a-box>    
  <a-sphere color="green"
            radius="0.5"
            position="-1 1.6 -2"
            animation="property:components.material.material.color;
                       type:color;
                       to:blue;
                       easing:linear;
                       dir:alternate;
                       loop:true;
                       dur:5000">
  </a-sphere>
</a-scene>

Einfache Erscheinungs- animation 1
Einfache Erscheinungs- animation 2

In Beispielprogramm 13 werden zwei Arten von Erscheinungsanimationen dargestellt: Die Änderung der Farbe der Kugel und die Änderung der geometrischen Form des Würfels. Dies funktioniert relativ analog zu Beispielprogramm 12. Die Skalierungsanimation des Würfels wird mit dem Stichwort scale aktiviert. Als Endzustand wurde to:0.5 1 2 gewählt, das heißt, dass der Würfel in die ${\textstyle x}$ -Richtung halbiert und in die ${\textstyle z}$ -Richtung verdoppelt wird, die ${\textstyle y}$ -Dimension bleibt dabei unverändert. Für die Farbänderung muss man <components.material.material.color; setzen. Dabei ist es wichtig, <type:color; dazu zu schreiben, wie es in der Dokumentation steht.

Modellierung der Umgebung

A-Frame ermöglicht es, sehr realistische 3D-Modelle zu konstruieren. Dabei ist es im Kontext von realitätsnahen VR wichtig, den passenden Hintergrund dazu zu erschaffen. Im Folgenden wird die Methode erläutert, wie man den Boden und Himmel typischerweise modelliert, siehe Beispielprogramm 14. Der einfachste Weg der Bodendarstellung ist die Zuhilfenahme einer Ebene. Das Kreieren der Ebene funktioniert mit dem A-Frame-Kommando <a-plane>. Dabei ist zu beachten, dass die Ebene normalerweise in ${\textstyle x}$ - ${\textstyle y}$ -Richtung erstellt wird. Daher muss man sie rotieren, wie es in Zeile 9 gemacht wird. Die Parameter height und width beschreiben die Größe der Ebene. Um es realistisch darzustellen, kann man eine Textur mit ggf. normal map drauf legen; hier wurde das passende Gras zum Baum gefunden .

Beispielprogramm 14

<a-scene>
  <a-entity position="0 3 -10"
            gltf-model="tree.gltf">
  </a-entity>
  <a-plane src="gras.jpg"
           normal-map="gras_nm.jpg"
           height="100"
           width="100"
           rotation="-90 0 0"
           repeat="100 100"
           normal-textured-repeat="100 100">
  </a-plane>           
  <a-sky src="lake.jpg"
         radius="50"
         position="0 0 0">
  </a-sky> 
</a-scene>

Zur Darstellung des Himmels wird üblicherweise der <a-sky>-Tag verwendet, siehe Zeile 13. Dabei ist es nichts Anderes als eine große Sphäre mit einem Radius, der groß genug ist. In diesem Beispiel wurde eine solche Textur verwendet – in Form eines ${\textstyle 360^{\circ }}$ -Bildes (siehe Aframe Sky).

Augmented Reality with AR.js

Es ist zu hoffen, dass es den Leser bereits davon überzeugte, dass A-Frame ein sehr vielseitiges und dennoch relativ einfach zu handhabendes Instrument ist, um VR-Szenen zu erschaffen. Dabei wurde nur die Spitze des Eisbergs betrachtet. Die Funktionalität von A-Frame bietet noch viel mehr. Insbesondere kann man mit minimalen Modifikationen den AR-Inhalt kreieren. Wie bereits erwähnt wurde, versteht man unter AR die erweiterte Realität, d. h. man erweitert die Realität mit virtuellen Komponenten.

Eine der Möglichkeiten ist das Bild der Kamera als Hintergrund der Szene zu benutzen. Jedoch ist die vorgeschlagene Lösung relativ komplex und für Personen ohne gute Vorkenntnisse in Webprogrammierung nicht gut nachvollziehbar. Ebenso ist das Resultat ziemlich verzerrt, denn Standard-Kameras produzieren ein normales flaches Bild, das auf die Sphäre projiziert wird. Im Beispielprogramm 14 wurde ein spezielles verzerrtes ${\textstyle 360^{\circ }}$ -Bild genau aus dem Grund verwendet.

Eine kanonische Vorgehensweise in der A-Frame-Community ist AR.js-Bibliothek. Diese bietet ein einfaches A-Frame-ähnliches Interface zur Erschaffung von AR-Inhalten und beinhaltet unter anderem auch Marker-Tracking-Features. Die Marker dienen dazu, die Position und Größe des VR-Objektes zu definieren. Der Marker wird erkannt und die Position des VR-Objektes wird an die Position des Markers gebunden; die Bewegungen und Rotationen des Markers werden dann auf das Objekt übertragen. Insbesondere wird der Marker benutzt, um die Transformation in ${\textstyle z}$ -Richtung zu erkennen - wird der Marker kleiner, entfernt sich das Objekt weiter. Marker dienen also als Anker für das Objekt im 3D-Raum.

Theoretisch kann man 3D-Informationen aus 2D-Bildern ohne Marker rekonstruieren; es gibt ausreichend viele Forschungsmaterialien in dieser Richtung. Ebenso wurden schon markerlose AR im AR.js erzielt Jerome Etienne, jedoch ist diese Technologie noch relativ neu und wird noch nicht offiziell unterstützt. Die Tutorials sind relativ komplex und unverständlich. Aus diesen Gründen wird der Fokus nur auf die markerbasierte Modellierung gelegt.

Integration von AR.js in A-Frame

Das Benutzen von AR.js in A-Frame ist relativ einfach, dazu gibt es mehrere Tutorials, z. B. Jerome Etienne ,Documentation. Anhand von Etienne, wurde ein Minimalbeispiel im Beispielprogramm 15 zusammengestellt. Das Beispiel zeichnet einen Würfel, sobald man den "Hiro"-Marker in die Kamera zeigt, siehe Abbildung Beispielprogramm 15.

Es ist zu erkennen, dass der Unterschied von AR (Beispielprogramm 15) zu VR (Beispielprogramm 1) ein 4-Zeilen-Code ist. Erstens wird hier die AR.js-Bibliothek in Zeile 5 angeknüpft, und mit Option <embedded arjs> in Zeile 9 eingeschaltet. Zweitens muss man der Kamera den Befehl geben, nach einem <"hiro"> Marker zu suchen; dies passiert in Zeile 11. Ebenso soll man die Kamera in Position ${\textstyle (000)}$ stellen, damit es so aussieht, als wäre das Objekt über dem Marker, wie es in Zeile 13 passiert. Hiro wird klassischerweise als Beispiel benutzt, allerdings kann man beliebige Muster zu Markern machen. Dies wird genauer im nächsten Unterkapitel erläutert.

Beispielprogramm 15

<<!DOCTYPE html>
<html>
  <head>
    <script src="https://aframe.io/releases/1.1.0/aframe.min.js"></script>
    <script src="https://jeromeetienne.github.io/AR.js/aframe/build/aframe-ar.js">
    </script>
  </head>
  <body>
    <a-scene embedded arjs>
      <a-marker preset="hiro">
          <a-box> </a-box>
      </a-marker>
      <a-camera position="0 0 0"> </a-camera>
    </a-scene>
  </body>
</html>>

Verwendung von "Hiro" Markern 1
Verwendung von "Hiro" Markern 2

Erstellen eigener Marker

Die Hiro und Kanji-Marker sind vordefiniert und werden durch die folgende Zeilen jeweils für die Darstellung der 3D-Objekte benutzt.

<a-marker preset="hiro">
<a-marker preset="kanji">

Jedoch können sie durch andere Marker ersetzt werden, die ggf. besser erkennbar machen, welche 3D-Modelle auf dem jeweiligen Marker dargestellt werden.

Die zwei unterstützten Arten, selbst erstellte Marker einzusetzen sind:

Patterns und
Barcodes.

Pattern - Muster

Die Patterns als quadratische Bildmuster sollten folgenden Anforderungen erfüllen:

(Schwarzer Rand) Als Marker qualifiziert sich jedes Bild, solange es eine schwarze Umrandung besitzt Etienne.
(Keine Symmetrie bzgl. Drehung) Eine Marker sollte keine Symmetrie bzgl. Drehung um 80,180 oder 360 Grad besitzen, denn ansonsten kann auf dem Markermuster das 3D-Modell nicht in eindeutiger Weise dargestellt werden, damit das 3D-Objekt im Kamerabild in eindeutiger Weise auf dem Marker dargestellt werden kann.
(Musterdetails) Ein 3D-Objekt sollte in unterschiedlicher Entfernung auf dem Marker im Kamerabild dargestellt werden können. Wenn die Detail auf dem Marker zu fein sind, kann eine Webcam mit der gegebenen Auflösung ggf. die Markerorientierung im Raum bei größerer Distanz zur Kamera ggf. nicht mehr auflösen.
(Kontraste) In einem Kamerabild sind durch Beleuchtung und Lichteinfall verschiedene Graustufen selbst auf einem weißen Papier erkennbar (z.B. Schatten). Wenn die Kontraste zwischen den verwendeten Farben groß sind, erhöht sich die Erkennungsgenauigkeit. Daher bietet sich bei schlechteren Lichtverhältnissen die Verwendung von groben, nicht drehsymmetrischen Schwarz-Weiß-Mustern an.

Anleitungen zur eigenen Markererstellung

Das AR.js-Entwicklungsteam publizierte Jerome Etienne eine ausführliche Anleitung zur Entwicklung der Marker, an der man sich größtenteils orientieren kann.

Es wurden drei verschiedene Pattern-Marker mithilfe vom Markergenerator Jerome Etienne erzeugt und getestet. Das Benutzen des Generators Jerome Etienne ist sehr einfach: Man lädt ein beliebiges Bild hoch, und erhält eine *.patt- und *.png-Datei des Markers zurück. Von den drei Markern hat der Irina-Marker am besten abgeschlossen: Er wurde am schnellsten erkannt, und es gab kaum Verzögerungen bei Bewegungen.

Erkennungsgenauigkeit

Jedoch hat keiner der erstellten Marker so gut funktioniert, wie der Standard Hiro- und Kanji-Marker. Der Grund dafür ist, dass der Farbkontrast relativ stark sein muss. Hellere Farben werden von der Kamera schlechter erkannt. Ferner ist es wesentlich, dass der Marker bzgl. der Symmetrie des inneren Markerbildes eindeutig festlegen muss, welche Seite "VORNE", "LINKS", "RECHTS", "HINTEN" definiert. Der erste Marker in den folgenden Abbildungen ist in dieser Hinsicht nicht eindeutig.

Beispiel-Marker mit unterschiedlichen Eigenschaften

Eigene Pattern-Marker 1
Eigene Pattern-Marker 2
Eigene Pattern-Marker 3

3D-Objekte auf Markern platzieren

Nach der Markererzeugung muss man dem AR.js und A-Frame mitteilen, dass das erzeugte Muster ein Marker ist. Dies ist sehr einfach realisierbar durch die Ersetzung von

<a-marker preset="hiro"> in Zeile 11 von Beispielprogramm 15.

durch die folgende Zeile möglich:

<a-marker type="pattern" url="marker.patt">

Mit <type="pattern"> sagt man aus, dass der Marker vom Pattern-Typ ist und mit der <url="marker.patt"> gibt man die Adresse an, in der die erzeugte *.patt-Datei sich befindet.

Ein Nachteil bei Pattern besteht darin, dass die Muster durch komplexe Bilder dargestellt werden. Wenn die Marker sich nicht so stark unterscheiden, ist es oft schwer, sie von einander zu differenzieren. Im Prinzip ist ein Bild nichts anderes als eine hoch-dimensionierte Matrix, deren Rekonstruktion bzw. Approximation auf komplizierten Algorithmen beruht, und meistens nicht mal gemacht wird. Die Unterscheidung von Bildern wird anhand gewisser Merkmale gemacht, sodass zwei verschiedene Bilder mit den selben charakteristischen Merkmalen gar nicht unterschieden werden können. Bei einem einfachen klein-dimensionierten Bild (z. B. ${\textstyle 3x3}$ Pixeln) hingegen ist das Muster viel einfacher zu erkennen.

Solche Bilder, deren Muster eindeutig erkennbar sind, nennt man Barcodes. Es gibt verschiedene Barcode-Arten. Heute unterscheidet man 1D-Barcodes (klassische Barcodes die z. B. in Geschäften benutzt werden, um Produkte zu identifizieren), 2D-Barcodes (z. B. DataMatrix oder QR), und 3D-Barcodes (z. B. farbige 2D-Barcodes).

In AR.js werden schachmusterartige Marker unterstützt. Diese werden sogar empfohlen in Szenen mit mehreren Markern Etienne aus den oben genannten Gründen. Hierbei muss beachtet werden, dass solche Muster klassischerweise mit einer Zahl in Verbindung gebracht werden. Z. B. kann man mithilfe von ${\textstyle 3x3}$ -schachbrettartigen Barcodes die Zahlen 0-63 kodieren. Daher sieht die Zeile 11 im Programm Beispielprogramm 15 für Barcodes beispielsweise wie folgt aus:

<a-marker type="barcode" value="5">

Die Zeile bedeutet, dass die Kamera nach dem Barcode suchen wird, der einer <"5"> entspricht. Ebenso muss man bei Barcodes die genauere Spezifikation des Markers in Zeile 9 angeben:

<a-scene embedded arjs="detectionMode:mono_and_matrix; matrixCodeType:3x3;">>

Hier steht ebenfalls, dass der Marker schwarzweiß ist und eine ${\textstyle 3x3}$ -Struktur besitzt, d. h. ein Schachbrett mit 9 Feldern. Die Marker mit den Zahlen 0-63 sind in [4] zu finden.

Ebenso kann man ${\textstyle 4x4}$ -, ${\textstyle 5x5}$ - oder ${\textstyle 6x6}$ -Muster verwenden, wenn man mehr als 64, 8192, oder 4194304 verschiedene Marker braucht. Der Barcode Generator [5] generiert verschiedene Barcodes in verschiedenen Formen. In den Abbildungen sind verschiedene Barcode-Marker-Beispiele dargestellt, die mithilfe des Barcode-Generators erzeugt wurden.

Eigene Barcode-Marker

Beispiel: Sonne-Erde-Mond-Dynamik

In diesem Kapitel wird ein Sonnen-Erde-Mond-Modell betrachtet: Die Erde rotiert um die Sonne und der Mond rotiert um die Erde. In der Wissenschaftsliteratur ist dieses Modell bekannt als Dreikörperproblem. Ebenso rotieren die Objekte um die eigene Achse. Diese Simulation eignet sich gut für Grundschüler der vierten Klasse, die die Grundlagen der Planetenbewegung erlernen sollen. Das Beispiel lässt sich mit wenig Aufwand auf das komplette Sonnensystem erweitern. Bevor die Implementierung erläutert wird, wird zuerst das betrachtete Modell genauer beschrieben.

Modellbeschreibung

Die genaue Dynamik dieser Bewegungen hängt mit dem geometrischen Themengebiet der Zykloide zusammen (siehe Animation). Zur Vereinfachung wird Folgendes angenommen:

Alle drei Objekte sind kugelförmig.
Die Bewegung aller drei Körper findet in der ${\textstyle x-z}$ -Ebene statt.
Die Bahnen der Planeten sind kreisförmig und die Bewegungsgeschwindigkeit konstant.
Alle Rotationen sind um die Achse parallel zur ${\textstyle y}$ -Achse; d. h. die Neigung der Achsen werden vernachlässigt.

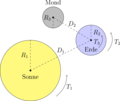
Um das Problem besser veranschaulichen zu können, wurde die Skizze angefertigt.

Sonne-Erde-Mond-Dynamik

Mit ${\textstyle R_{1}}$ , ${\textstyle R_{2}}$ und ${\textstyle R_{3}}$ bezeichnet man die Radien der Objekte. Die Distanzen ${\textstyle D_{1}}$ und ${\textstyle D_{1}2}$ bezeichnen die Abstände von der Erde zur Sonne und von der Erde zum Mond. Mit ${\textstyle T_{1}}$ wird die Zeit bezeichnet, in der die Erde eine volle Umdrehung um die Sonne macht. Mit ${\textstyle T_{2}}$ bezeichnet man die Zeit, die benötigt wird für eine volle Umkreisung des Mondes um die Erde. Der Mond rotiert nicht um die eigene Achse. Es ist bekannt, dass der Mensch nur ein und die selbe Seite des Mondes zu sehen bekommt. Jedoch rotiert die Erde um ihre eigene Achse. Deren Rotationsgeschwindigkeit wird mit der Periodenzeit ${\textstyle T_{3}}$ bezeichnet. Ebenso werden die Maße nicht maßstabsgetreu skaliert, um eine bessere Veranschaulichung zu schaffen. Die Größe der Erde ist im Vergleich zur Sonnengröße vernachlässigbar; die maßstabstreue Skalierung würde dazu führen, dass man die Erde und den Mond nicht erkennen kann. Alle verwendeten Größen sind gewählt wie in der Tabelle angegeben.

${\textstyle R_{1}}$	${\textstyle R_{2}}$	${\textstyle R_{3}}$	${\textstyle D_{1}}$	${\textstyle D_{2}}$	${\textstyle T_{1}}$	${\textstyle T_{2}}$	${\textstyle T_{3}}$
${\textstyle 0.5}$	${\textstyle 0.125}$	${\textstyle 0.0525}$	${\textstyle 1}$	${\textstyle 0.3}$	${\textstyle 100}$	${\textstyle 10}$	${\textstyle 0.5}$

Implementierungsvorgehen

Um das Problem in A-Frame veranschaulichen zu können, werden drei Platzhalter für Sonne, Erde und Mond benötigt; im Folgendem als Entity 1, Entity 2 und Entity 3 bezeichnet. Entity 1 dient dazu, die Bewegung um die Sonne zu beschreiben. Innerhalb von Entity 1 wird Entity 2 platziert, verschoben um ${\textstyle D_{1}}$ . Somit rotiert Entity 2 um die Achse im Zentrum von Entity 1. Innerhalb von Entity 2 wird ebenfalls eine Rotation definiert und Entity 3, verschoben um ${\textstyle D_{2}}$ , platziert.

Dieses Beispiel lässt sich vermutlich auch ohne das Entity-Konzept genau so realisieren, wie es im Beispielprogramm 12 gemacht wurde, jedoch liefern die Entities bewegliche lokale Koordinatensysteme, sodass die Objekte nur noch richtig platziert werden müssen.

Um die Idee besser veranschaulichen zu können, wurde folgender Algorithmus als Pseudocode gefertigt.

Algorithmus 1 Pseudocode zu Sonne-Erde-Mond-Bewegungen

Anfang Entity1
Setze Position = ${\textstyle (0,0,0)}$
Rotation = ${\textstyle (0,T_{1},0)}$
Sonne
Anfang Entity2
Setze Position = ${\textstyle (D_{1},0,0)}$
Setze Rotation = ${\textstyle (0,T_{2},0)}$
Erde
Anfang Entity3
Setze Position = ${\textstyle (D_{2},0,0)}$
Mond
Ende Entity3
Ende Entity2
Ende Entity1

Hierbei ist zu beachten, dass die Objekte durch das Rotieren der Platzhalter ebenso mitrotieren. Wenn die Sonne beipielsweise innerhalb von Entity 1 platziert wird, wie im Algorithmus 1 dargestellt ist, rotiert die Sonne mit. Dies kann man umgehen, indem man innerhalb der Sonnensphäre eine interne Gegenrotation einfügt, oder man platziert die Sonne außerhalb der Entity 1, wie es im Beispielprogramm 6 gemacht wurde. Diese Technik wird auch hier verwendet. Ebenso würde der obige Psedocode dazu führen, dass die Rotationsgeschwindigkeit des Mondes um die Erde gleich der Rotationsgeschwindigkeit der Erde um die eigene Achse wäre. Das heißt, dass der Mond immer nur von einer Seite der Erde gesehen wird. Deshalb lässt man die Rotation innerhalb von Entity 2 der Geschwindigkeit entsprechen, mit der der Mond um die Erde kreist. Die Rotation der Erde um die eigene Achse passt man mit der internen zusätzlichen Rotation (innerhalb der Sphärenumgebung) entsprechend an.

Der Programmcode ist im Beispielprogramm 16 dargestellt.

Beispielprogramm 16

<a-scene>
  <a-sphere radius="0.5"
            src="sonne.jpg">
  </a-sphere>
  <a-entity animation="property:rotation; 
                       to:0 360 0; 
                       dur:100000; 
                       loop:true; 
                       easing:linear">
    <a-entity position="1 0 0"
              animation="property:rotation; 
                         to:0 360 0; 
                         dur:10000; 
                         loop:true; 
                         easing:linear">
      <a-sphere radius="0.125"
                src="erde.jpg"
                animation="property:rotation; 
                           to:0 360 0; 
                           dur:1000; 
                           loop:true; 
                           easing:linear">
      </a-sphere>
      <a-entity position="0.3 0 0">
        <a-sphere radius="0.0525"
                  src="mond.jpg">
        </a-sphere> 
      </a-entity>
    </a-entity>
  </a-entity>
  <a-sky radius="50"
         src="sternhimmel.jpg"
         repeat="20 20">
  </a-sky>
</a-scene>

Planetensystem 1
Planetensystem 2
Planetensystem 3

Hierbei kann man anmerken, dass die Entity 3 nicht notwendigerweise gebraucht wird. Man kann genauso den Mond in Position ${\textstyle (D_{2},0,0)}$ platzieren. Allerdings liefert uns Entity 3 eine gewisse Freiheit: Man kann damit beispielsweise die Rotation des Mondes um die eigene Achse verwirklichen. Um es so realistisch wie möglich zu gestalten, wurden Texturen für Planeten und ein Sternbild für den Himmel verwendet, die man in Textur-Universum finden kann. Hier wurde auf normal-maps verzichtet, da der Effekt kaum zu sehen ist.

Markerbasierte Realisierung

Das Modell lässt sich auch auf Marker übertragen. Beispielprogramm 17 auf dem Hiro-Marker^[3] zeigt, wie das entwickelte Sonne-Erde-Mond-Modell auf Hiro-Marker projiziert werden kann. Die dazu benötigten Schritte sind genau wie im Kapitel "Augmented Reality with AR.js" beschrieben, und werden daher nicht wiederholt. Das Verwenden des Hintergrundes ist in AR überflüssig, sodass <a-sky> wegfällt.

<a-scene> embedded arjs>
 <a-marker preset="hiro">
   <a-sphere radius="0.5"
             src="sonne.jpg">
   </a-sphere>
   <a-entity animation="property:rotation; 
                        to:0 360 0; 
                        dur:100000; 
                        loop:true; 
                        easing:linear">
     <a-entity position="1 0 0"
               animation="property:rotation; 
                          to:0 360 0; 
                          dur:10000; 
                          loop:true; 
                          easing:linear">
       <a-sphere radius="0.125"
                 src="erde.jpg"
                 animation="property:rotation; 
                            to:0 360 0; 
                            dur:1000; 
                            loop:true; 
                            easing:linear">
        </a-sphere>
        <a-entity position="0.3 0 0">
          <a-sphere radius="0.0525"
                    src="mond.jpg">
          </a-sphere> 
        </a-entity>
      </a-entity>
    </a-entity>
  </a-marker>
  <a-camera position="0 0 0"> </a-camera>
</a-scene>

Planetensystem am Hiro-Marker 1
Planetensystem am Hiro-Marker 2
Planetensystem am Hiro-Marker 3

JASON3D4AframeEditor for Aframe

Der Jason3D4Aframe-Editor für Aframe erleichtert das Erstellen von 3-D-Modellen dadurch, dass man hierbei keine HTML-Kenntnisse aufweisen muss. Das Interface des Editors und darin vorhandenen Werkzeuge und Interaktionsmöglichkeiten ermöglicht es jedem, online sein 3-D-Modell zu erstellen.

Auch hier sind einfache geometrische Figuren und weitere Vorlagen bereits vorprogrammiert, die dann genutzt und modifiziert werden können. Bereits vorhanden sind Würfel, Kegel, Zylinder, Ellipsoid, Prisma, Pyramide, Sphäre, Torus, Bogen, Kreis, Ebene, Ring, Dreieck und ein möglicher Text. Diese Objekte können dann gemäß deren Eigenschaften in Höhe, Breite, Tiefe oder Radius verändert und sowohl farblich als auch in ihrer Transparenz angepasst werden. Zudem ist es möglich, Objekte mittels eines kartesischen Koordinatensystems auf der x, y und z-Achse im Raum zu verschieben. Gemäß dieser Achsen ist es auch möglich, die Objekte in Gradschritten zu drehen. Möchte man ein größeres 3-D-Modell erstellen, besteht die Möglichkeit, die einzelnen Objekte zu benennen und wie Ebenen durchzuwählen. Das aktuelle Objekt oder Modell wird dabei durchgängig in Echtzeit in einem Beispielfenster in der Mitte angezeigt und kann auch als Vorschau vergrößert werden.

Bei einem fertigen Modell aus mehreren Objekten ist es möglich, dieses insgesamt zu skalieren oder im Raum zu verschieben.

Um das erstellte Modell in ein Augmented Reality Setting zu integrieren, kann es auf einen Hiro- oder Kenji-Marker gesetzt werden. Die Überprüfung kann dann direkt im Editor unter "Preview 3D", wenn "AR-Marker 3D" ausgewählt ist, mit der Kamera und dem passenden Marker getestet werden.

Möchte man nun eine Virtual-Reality-Umgebung mit seinem Modell erschaffen, ermöglicht der Editor das Hinzufügen von verschiedenen 360-Grad-Hintergründen, wie bspw. Wolken und Gras oder das Amphitheater in Berlin.

Das vorerst fertige Modell kann nun als .json-Datei gespeichert werden, die im Editor erneut geöffnet und bearbeitet werden kann oder als .html-Datei, die dann den Quelltext für eine Integration in eine Webseite bietet.

Diese Integration wäre dann kostenlos und dauerhaft über Github.com möglich. Eine passende Anleitung, wie man 3-D-Modelle und auch 360-Grad-Bilder damit auf einer Webseite integriert ist in der Readme-Datei des Projekts zur St. Maria Kirche in Landau in der Pfalz genauer erklärt.

Beispiel: 3-D-Modell St. Maria Kirche in Landau in der Pfalz

Hierbei handelt es sich um ein 3-D-Modell der Kirche St. Maria in Landau in der Pfalz. Das Modell wurde aus verschiedenen geometrischen Körpern erstellt, welche zusammen die Form der Kirche wiederspiegeln sollen. Das Modell eignet sich für den Grundschulunterricht einer vierten Klassen zum Identifizieren von geometrischen Körpern in der Umwelt/Gebäuden und um diese mit Bauwerken in Verbindung zu bringen.

Modellbeschreibung

In dem hier dargestellten Modell wurden nur geometrische Körper verwendet, die auch in der Grundschule zum Einsatz kommen können. Daher besteht nur aus verschieden großen Quadern, Pyramiden und Prismen. Zusätzlich wurden die einzelnen Körper verschieden transparent eingefärbt, damit sie besser identifiziert und unterschieden werden können.

Fotos des 3-D-Modells der Kirche

Siehe auch

Quellennachweis

↑ Chen, P., Liu, X., Cheng, W., & Huang, R. (2017). A review of using Augmented Reality in Education from 2011 to 2016. Innovations in smart learning, 13-18.
↑ Nils Schatzmann (2024) 3-D-Modell der St. Maria Kirche in Landau - GitHub-Repository: https://github.com/Schatz234/Kirche Vorschau des Modells: https://schatz234.github.io/Kirche/kirche_st_maria_ar_hiro.html
↑ Hiro-Kanji-Marker Druckvorlage (2017) PDF-Dokument - Zum Ausdrucken und Aufkleben auf Pappstreifen - Download: https://niebert.github.io/JSON3D4Aframe/pdf/marker_hiro_kanji_printout.pdf JSON3D4Aframe

[1] Chen, P., Liu, X., Cheng, W., & Huang, R. (2017). A review of using Augmented Reality in Education from 2011 to 2016. Innovations in smart learning, 13-18.

[2] Nils Schatzmann (2024) 3-D-Modell der St. Maria Kirche in Landau - GitHub-Repository: https://github.com/Schatz234/Kirche Vorschau des Modells: https://schatz234.github.io/Kirche/kirche_st_maria_ar_hiro.html

[3] Hiro-Kanji-Marker Druckvorlage (2017) PDF-Dokument - Zum Ausdrucken und Aufkleben auf Pappstreifen - Download: https://niebert.github.io/JSON3D4Aframe/pdf/marker_hiro_kanji_printout.pdf JSON3D4Aframe

[1]

[2]

[3]